Interfering with influenza: nonlinear coupling of reactive and static mitigation strategies

Abstract

When new, highly infectious strains of influenza emerge, global pandemics can occur before an effective vaccine is developed. Without a strain-specific vaccine, pandemics can only be mitigated by employing combinations of low-efficacy pre-pandemic vaccines and reactive response measures that are carried out as the pandemic unfolds. Unfortunately, the application of reactive interventions can lead to unintended consequences that may exacerbate unpredictable spreading dynamics and cause more drawn-out epidemics. Here, we employ a detailed model of pandemic influenza in Australia to simulate the combination of pre-pandemic vaccination and reactive antiviral prophylaxis. This study focuses on population-level coupling effects between the respective methods, and the associated spatio-temporal fluctuations in pandemic dynamics produced by reactive strategies. Our results show that combining strategies can produce either mutual improvement of performance or interference that reduces the effectiveness of each strategy when they are used together. We demonstrate that these coupling effects between intervention strategies are extremely sensitive to delay times, compliance rates and the type of contact targeting used to administer prophylaxis.

1. Introduction

Epidemic processes share the general feature of a transition from vanishing to extensive spreading, separated by a threshold in the propensity of the contagion to transmit from infected to susceptible individuals [1–6]. A practical consequence of this nonlinearity is that influenza outbreaks become pandemics only when the transmissibility of the disease among individuals and the flux of individuals among locations are high enough for extensive spreading to occur on the global scale. Therefore, to mitigate the spread of a pandemic, interventions must effectively reduce the ability of the virus to transmit between people and locations, so that herd immunity is achieved [7,8].

Vaccination programmes with a tailored, strain-specific vaccine are widely considered the most effective single method for limiting the spread of an infectious virus. However, because pandemics typically occur with the emergence of new viral strains, high-efficacy vaccines are usually not available in time to mitigate the spread of the disease using pre-pandemic vaccination alone. In light of this, most pandemic modelling studies that include the use of pre-pandemic vaccines assume a rather limited efficacy, and therefore require the additional application of other, reactive intervention methods in order to successfully contain the spread. Numerous simulation studies have been performed using a variety of modelling frameworks and model populations that all reach the same conclusion: highly infectious pandemics can only be mitigated by combining multiple strategies that act on different mechanisms in parallel to reduce susceptibility and infectiousness [9–15].

The theoretical picture becomes much more complex when reactive strategies are applied, as these alter the properties of the contagion non-uniformly in space and time. Previous modelling results suggest that unintended consequences can occur, such as the prolongation of an epidemic. For example, owing to logistical constraints, reactive intervention strategies cannot be maintained continuously, which produces fluctuations in the population’s susceptibility, resulting in more drawn-out epidemics [14,16–18].

In this work, we explore the combination of pre-pandemic vaccination and reactive antiviral prophylaxis, with a focus on nonlinear coupling effects between the respective methods. We demonstrate that these coupling effects are extremely sensitive to delay times, compliance rates and the type of contact targeting used to administer prophylaxis. Our results show that combining strategies can produce either mutual improvement of performance or interference that reduces the effectiveness of each strategy when they are used together.

To simulate detailed intervention strategies, it is necessary to model the spread of the pandemic in both space and time, while explicitly accounting for recurrent mobility patterns and the clustered contact structure of the population over which the pandemic spreads. These attributes are difficult or impossible to incorporate into standard continuum frameworks or metapopulation models because local variations in community structure and contact patterns violate the assumptions of homogeneity typically made in their formulation [19–21]. Rather than attempt to describe the population’s complex features within an expanded, high-resolution, multiplex metapopulation framework [22], we employ an individual-based model of an entire nation (Australia), with a population of approximately 23 million (at the time of the most recent census, 2016). Through a detailed calibration with census data from 2016, we model demographic heterogeneity and clustering of social interactions through household, neighbourhood, school and workplace environments which are fundamental to understanding departures from continuum dynamics that can easily be captured by stochastic, individual-level models [23]. Upon this surrogate Australian population, we simulate pandemic influenza using a stochastic discrete-time model of disease spread. (See the Methods section and electronic supplementary material, S1 for detailed descriptions of population structure and pandemic transmission simulations. Electronic supplementary material, figure S1 provides a schematic of the population structure that we derive from census data, as described in our previous publications [24,25].)

We have previously used this model to investigate spatial hierarchies and epidemic synchrony and to simulate the role of urbanization in the spatio-temporal dynamics of simulated pandemics in the Australian context [24,25]. Here, we extend our modelling framework to incorporate reactive interventions. The main contributions of this work can be summarized in two points:

• —A characterization of the spatio-temporal fluctuations in contagion dynamics brought about by the application of reactive intervention strategies.
• —A detailed investigation of the nonlinear coupling between combined static and reactive strategies (pre-pandemic vaccination and targeted antiviral prophylaxis, in this case).

1.1. Mitigation strategies

While many of the strategies tested in previous studies involve three or more distinct types of interventions, including targeted vaccination, travel restrictions, household quarantine, reactive school closure and targeted antiviral prophylaxis, we focus here on a relatively simple system of interacting mitigation techniques. Specifically, we examine uniform treatment with a pre-pandemic vaccine at a specified compliance rate (random pre-pandemic vaccination), in combination with targeted deployment of antivirals to treat identified index cases and provide prophylaxis to their neighbourhoods (geographically targeted antiviral prophylaxis, GTAP) or contacts (TAP). In this work, we use the abbreviations TAP and contact-TAP interchangeably to refer to contact-targeted antiviral prophylaxis.

This choice of intervention strategies is relevant because these methods are widely included in the pandemic response plans of industrialized nations [26–29]. It is also pragmatic from a modelling perspective because their pharmacological mechanisms are distinct, allowing us to reasonably exclude drug interactions within individuals. In addition, they are well-established measures in the pandemic modelling literature, and should be familiar to most expert readers [9–13,16,17,30,31]. With respect to the choice of antiviral prophylaxis as a relevant subject, Australia’s national pandemic preparedness plan includes the targeted use of antivirals among its list of pharmaceutical control measures. The federal government maintains a reasonably large antiviral stockpile of several tens of millions of courses [32,33], and the deployment of those resources has been a persistent feature of policy-related modelling studies in the Australian context [18,34].

The consideration of only pharmaceutical methods is convenient from a modelling perspective because it allows a relatively simple implementation of the programme, without having to simulate the topological changes in population interaction structure brought about through social distancing and behaviour modification [35,36]. These effects are important in epidemiological modelling in general, and, indeed, human behaviour can have dramatic effects on compliance with pharmaceutical delivery programmes [37]. However, our focus here is not on simulating an elaborately optimized system of interventions, but rather on demonstrating how coupled methods interact in a relatively simple but reasonably realistic test case. As much as possible, we want to avoid the common issue of a combinatoric explosion of simulation parameters that is frequently encountered in pandemic intervention modelling studies (see Milne et al. [34] for an illustrative example). Even with our relatively conservative scope, the scale and complexity of our model imposes significant limitations on our study that must be left to future work.

In this study, we focus on the essential roles of two important factors, which we encode as control parameters in our simulations. These are:

• —compliance rate, which is the fraction of those scheduled for treatment who decide to participate in the programme
• —delay time, which characterizes the interval between identification of index cases and the successful deployment of antivirals to their contacts or neighbourhoods.

We chose these two parameters because they have been broadly identified in many previous studies as crucial to the success of mitigation strategies.

The role of compliance is usually intuitive: the larger the number of susceptible people who participate in the prophylaxis programme, the more successful it will be (we therefore expect monotonic behaviour of overall illness rates as a function of compliance). The role of delay time is more nuanced, as it is a less well-studied factor, and conflicting results have been published with respect to the effects of timing on both illness suppression and cost-effectiveness [14,16,17]. In the approach taken here, we investigate the effects of logistical deployment time to specific localities or social clusters, which aligns with the interpretation taken by Black et al. [38] in their investigation of antiviral administration to households. Other models interpret delay time as a universal property that controls the global implementation of measures [9,10].

Because we model delay time on the scale of targeted sub-populations, our simulations capture the imposition of spatially localized temporal fluctuations in the rate of transmission. As we will show, these heterogeneous interventions have complex effects on epidemic dynamics that can alter the efficiency of reactive strategies. (A full description of our implementation of the mitigation strategies is included in the electronic supplementary material, section S1. A flow chart for the intervention algorithm is included in electronic supplementary material, figure S2, for which table S1 defines the symbols used in the flow chart.)

2. Results and discussion

Our results are organized into three sections. First, we present simulation results for the individual mitigation strategies (pre-pandemic vaccination, contact-TAP and GTAP). We then use the same format to present the results of mixed strategies applying antiviral prophylaxis to a population already treated with a pre-pandemic vaccine at a compliance rate of 70%. Finally, we investigate coupling between the combined strategies over the [delay time] × [compliance rate] parameter space.

2.1. Pre-pandemic vaccination

To provide context for our results using mixed strategies, we begin by discussing the effects of the component strategies (vaccination and antiviral prophylaxis) individually. The pre-pandemic vaccination programme we simulate is simple: prior to the first index case reaching Australian cities, each individual has an independent probability of being vaccinated. This probability is the compliance rate for the simulation, and determines the level of suppression imparted by the vaccination programme, as the efficacy (the effect of the vaccine on individuals) is fixed. Specifically, a vaccinated individual is only 50% as likely to become infected as an untreated individual for the same force of infection from contacts. In addition, if a vaccinated individual becomes infected, their contribution to the force of infection on contacts is reduced by 30% relative to what it would have been had they not been vaccinated. Our simulations occur over a time interval of only 250 days, so we neglect complex factors associated with viral evolution in the presence of imperfect vaccination for the present study [39].

2.1.1. Reproductive ratio

The reproductive ratio of the disease (R₀) is defined as the expected number of secondary cases produced by a typical infected individual introduced to a completely susceptible population. Epidemics cannot spread extensively if R₀ < 1, which defines the critical threshold of infectiousness above which epidemics are possible. In this work, we treat R₀ as a measure of the infectiousness of the disease in the absence of any mitigation efforts, which is an increasing function of the global infectivity multiplier κ (see the electronic supplementary material for transmission model details).

It is possible in principle to analytically determine R₀ as the dominant eigenvalue of the next-generation matrix accounting for the heterogeneous population structure (e.g. [40]). A related method is to estimate R₀ from an explicit contact network structure using the epidemic percolation network (EPN) approach [41]. However, the size and complexity of our agent-based model makes these rigorous methods intractable.

Instead, we apply stochastic sampling of index cases to estimate R₀ numerically. To calibrate between R₀ and explicit values of κ, we average over many (n ≈ 10⁴) micro-simulations, introducing a single randomly selected index case and counting the number of secondary infections produced between infection and recovery of that individual. In this calibration scheme, only the force of infection produced by the index case is taken into consideration. That is, secondary infections caused by the index case do not exert a force of infection, so that all cases counted can be unequivocally attributed to the index case chosen in a given instance.

Owing to biases introduced by uniform sampling of index cases, we modified the R₀ estimation procedure used by Cliff et al. [24] and Harding et al. [42] to account for the non-uniform probability of infection in different population cohorts as described by Germann et al. [9]. Specifically, we biased the selection of index cases based on age-stratified attack rates. This technique produces a much better estimate of R₀ because of the inhomogeneous population structure which makes school-aged children and their parents more likely to become infected during an epidemic. The details of these age-stratified attack rate and R₀ computations are included in electronic supplementary material, figure S3.

2.1.2. Pre-pandemic vaccination

The performance of pre-pandemic vaccination programmes is illustrated in figure 1, which shows that the low-efficacy pre-pandemic vaccine simulated here is not capable of providing substantial herd immunity for highly infectious pandemics (R₀ = 2.23; as a comparison, the R₀ value for the 2009 H1N1 pandemic strain was estimated at approx. 1.5 [43]). This limited population-level illness suppression is demonstrated by the lack of a pronounced threshold for attack rate as vaccine compliance increases. Electronic supplementary material, figure S4 contains more details on the sensitivity of the vaccination programme performance to different values of R₀ and compliance. These results show that, as expected, suppression through vaccination alone is possible if R₀ is sufficiently low. However, because of the persistent influx of new index cases in our simulation scenario, full eradication is not observed.

Figure 1.

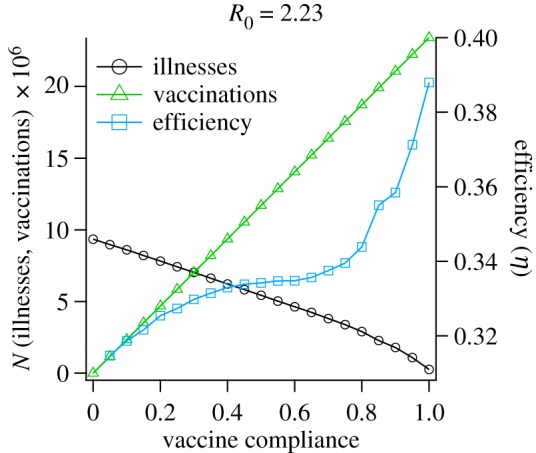
Performance of simulated pre-pandemic vaccination programmes, for different values of compliance. The left y-axis plots attack rate and number of vaccinations, while the right y-axis plots the efficiency of each treatment (suppressed illnesses per vaccination). The x-axis represents the proportion of the population vaccinated. For these simulations, the basic reproductive number was fixed (R₀ = 2.23), corresponding to a highly infectious pandemic strain. Symbols correspond to average values over 10 independent runs, the lines connecting them are guides to the eye.

To provide a rudimentary estimate of relative cost-effectiveness, we plot the ratio of illnesses prevented to vaccines delivered, which we refer to as the efficiency of the single-component mitigation strategy,

$${\eta }_i=\frac{I_o-I_i}{c_i},$$ 2.1

where I_o is the expected attack rate in the absence of intervention, I_i is the attack rate using the intervention programme i and c_i is the number of administrations of intervention programme i. If we define the suppression attributable to strategy i as σ_i = I_o − I_i, then the efficiency can be written simply as the ratio η_i = σ_i/c_i.

The efficiency is the average number of cases averted by each individual administration of the intervention programme (vaccines, in this case). If herd immunity effects are introduced as compliance increases, the efficiency should increase dramatically, followed by saturation and an eventual drop after passing the herd immunity threshold beyond which additional vaccinations are unnecessary.

Although pre-pandemic vaccination is not capable of completely mitigating the epidemic, figure 1 does show slight nonlinearity in the attack rate for values of vaccine compliance greater than ≈0.8, corresponding to a significant increase in the efficiency, which begins to noticeably increase as compliance exceeds $\approx 70\text{\%}$. This departure from linear behaviour indicates that the system is approaching the critical amount of suppression needed for containment. Based on this observation, it is reasonable to expect that the concomitant application of reactive policies with pre-pandemic vaccination could tip the scales in favour of containment, given sufficiently complete vaccine compliance. In our explorations of mixed intervention strategies, we intentionally place the system near this threshold by setting R₀ = 2.23 and vaccine compliance to 70% in order to investigate coupling of the combined strategies near the transition to containment.

2.2. Reactive strategies: targeted antiviral prophylaxis

In our study of reactive antiviral prophylaxis strategies, we investigated two different targeting programmes: geographic targeting, in which antivirals are distributed to the residential neighbourhoods of index cases, and contact targeting, in which the immediate contacts of index cases at work, school and home environments receive prophylaxis. In both targeting programmes, all ill individuals who seek medical services are treated with antivirals to alleviate symptoms, which partially reduces transmission strength from the treated individuals after a lag time of 1 day. If an ill individual seeks treatment and has contacts who are not already scheduled for prophylaxis, they will be designated as an index case and their contacts or neighbours will be scheduled for antiviral provision.

The delivery of antivirals occurs after a logistical delay time that we systematically vary in our study. Only a fraction of identified contacts actually take antivirals, which we interpret as an independent probability (the compliance rate). In real terms, compliance rates less than 1 could correspond to any combination of factors that limit the completeness of targeting, inhibit delivery of products or negatively influence people’s willingness to take the delivered pharmaceuticals.

An individual taking antivirals is less likely to contract influenza; if they do become infected, they are less infectious and only half as likely to express symptoms. Note that this effect of antivirals represents a countervailing factor that can have unfortunate population-scale effects on contagion spread, as asymptomatic individuals cannot be ascertained as index cases [44]. An infected individual treated for symptoms takes antivirals at a higher dosage for 5 days, while an individual receiving prophylaxis takes antivirals for 10 days (this is not modified if the person becomes ill while taking prophylaxis). We assume that the effects of antivirals cease after the dosage period ends.

Importantly, index case detection is not deterministic, and occurs only for symptomatic cases with a probability of 0.1 on each day of symptom expression (because of the distribution of illness duration in our model, this averages to an expected detection probability of ≈0.27). Imperfect index case detection is an essential aspect of our modelling framework, as it has been shown to dramatically alter the performance of simulated antiviral prophylaxis strategies in continuum models [45]. It is worth noting that, while our detection probability corresponds to a minority of cases and is low compared with that used in the work by McCaw et al. [45], it is close to the value ascertained from seroprevalence data after the first wave of the 2009 pandemic in the UK (if a 30% asymptomatic fraction is assumed) [46].

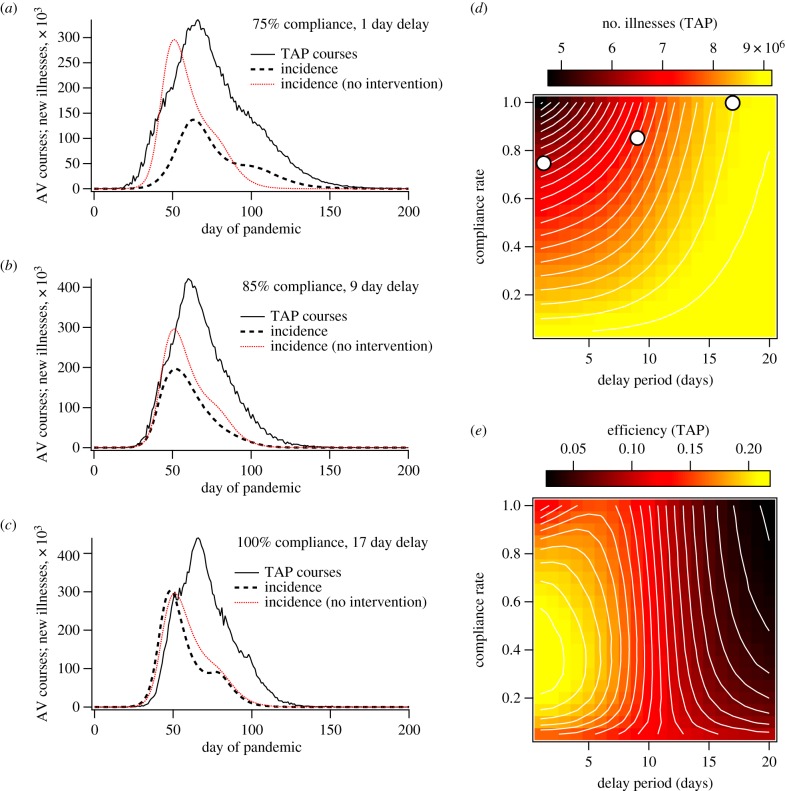
In accordance with our goal of investigating situations for which combined strategies are essential to pandemic suppression, we simulated the performance of these reactive programmes for the case of a highly infectious strain (R₀ = 2.23). Figure 2 and electronic supplementary material, figure S5 illustrate the behaviour of TAP and GTAP, respectively, as functions of the delay time between detection of index cases (from 1 to 20 days) and compliance rate within targeted groups (from 0% to 100%).

Figure 2.

Simulation results for contact-TAP with R₀ = 2.23 (without a pre-pandemic vaccination programme). (a–c) The incidence of new illnesses and antiviral (AV) courses deployed as functions of time for single simulation instances using (a) 75% compliance rate and a 1 day delay period between contact identification and prophylaxis, (b) 85% compliance and a 9 day delay, and (c) 100% compliance and a 17 day delay. For reference, the red curves illustrate the average incidence when no intervention method is used. The simulations that generated plots (a–c) used the same random number seed to control for stochastic initial conditions. Plots (d) and (e) demonstrate the attack rate and efficiency, respectively, as functions of compliance and delay period. The white circles in (d) mark the points of parameter space from which plots (a–c) were drawn.

2.3. Contact-targeted antiviral prophylaxis

Contact-targeting specifically focuses attention on those most likely to be in immediate danger of becoming infected. Therefore, under circumstances in which all cases are symptomatic, all index cases are ascertained, all contacts are identified, delivery of antivirals is immediate, the prophylaxis period is long compared with the epidemic generation time, and the efficacies of antivirals and vaccines are identical, the suppression due to prophylaxis will mimic exactly that of random pre-pandemic vaccination [30]. However, in the cases investigated here, every one of these conditions is relaxed, and the performance of targeted antivirals is difficult to predict a priori.

Figure 2a–c demonstrates the temporal behaviour of the pandemic TAP programme for selected sets of parameters. Comparison of these plots reveals several important results:

• —Figure 2a shows that, if the delay time is sufficiently short, the initial growth rate of the pandemic can be slowed, giving results that resemble those for pre-pandemic vaccination (with a later, smaller incidence peak).
• —Figure 2b demonstrates that the direct effect on the pandemic growth rate disappears as the delay time increases; however, the attack rate and peak incidence can still be suppressed significantly, suggesting effects on time scales longer than the single-generation events to which the TAP protocol is tailored.
• —Figure 2c shows that these ‘secondary’ effects are still delay-time dependent and vanish with long delay times, for which the deployment of antivirals has little effect, even for very high compliance rates.

The image plots in figure 2d,e show the attack rate and efficiency, respectively, as functions of compliance and delay time. They illustrate a conundrum: efficiency and suppression are not monotonically related, and the area with highest suppression does not demonstrate maximum efficiency. Instead, for short delay times, efficiency increases to a maximum near 40% compliance and then decreases monotonically as compliance and suppression both increase.

This is most likely because prophylaxis can slow the spread of the epidemic within localized pools of susceptible individuals, while still allowing the virus to survive. Once the prophylaxis period ends, resurgence of the virus through the treated communities can occur, and subsequent rounds of prophylaxis become necessary to prevent illnesses, leading to a substantial drop in efficiency. This phenomenon gets more prominent with higher compliance rates, for which ‘sub-critical’ intervention policies extend the time scale of epidemic spread more substantially, requiring more rounds of prophylaxis, each of which requires a large outlay of resources due to the high compliance rate.

The fact that total antiviral administration numbers exceed the total population over portions of parameter space confirms that this mechanism is occurring (see electronic supplementary material, figure S7 for plots of antiviral administration numbers). While a thorough quantitative analysis of local dynamics is planned for a future study, we provide a qualitative description in the electronic supplementary material. Specifically, high-resolution movies of disease spread through Australia are provided that correspond to the incidence plots shown in figure 2a. These are shown in electronic supplementary material, movies SM1 (no intervention) and SM3 (TAP).

When geographical targeting is implemented, suppression levels are higher, but efficiency drops off very rapidly for high compliance rates and suppression levels. GTAP requires prohibitively high numbers of antivirals for implementation in the programme described here. These results are detailed in electronic supplementary material, figure S5, which provides data on GTAP performance for comparison with the TAP data shown in figure 2. In addition, electronic supplementary material, movie SM4 illustrates the spatio-temporal spread of the virus when GTAP is implemented, corresponding to electronic supplementary material, figure S5a.

2.4. Coupled strategies

We now turn to the main subjects of this study, which are the performances and properties of mitigation strategies that combine pre-pandemic vaccination with reactive response measures (TAP or GTAP). In these scenarios, the pre-pandemic vaccine is applied as described above, followed by the introduction of the pandemic and a reactive programme of antiviral prophylaxis. The effects of the coupled pharmaceuticals are cumulative: if an individual is given both vaccine and antivirals the efficacies multiply as though the mechanisms act independently in parallel. While this approximation is likely to be an oversimplification of the complex behaviour of human immune response and antiviral enzyme inhibition, we consider it reasonable as the two classes of drugs have distinct mechanisms, and the acute activity of the pre-pandemic vaccine is considered stabilized before introduction of the antivirals.

Representative results of our simulations combining TAP and GTAP with pre-pandemic vaccination are shown in figure 3 and electronic supplementary material, figure S6, respectively.

Figure 3.

Simulation results for contact-TAP, in combination with pre-pandemic vaccination at 70% compliance. Plots (a–c) show antiviral (AV) course deployments and incidence of new illnesses as functions of time for selected TAP compliance rates and delay periods. The green traces in (a–c) correspond to the illness incidence for the case of 70% vaccine compliance. Plots (d) and (e) show attack rate and efficiency per course, respectively, as functions of TAP compliance rate and delay time. For (e), efficiency was computed as total illness suppression divided by the sum total of vaccinations and antiviral courses deployed. With the exception of those used to define the mitigation protocols, the simulation parameters used to generate these plots were the same as those used for figure 2 and electronic supplementary material, figure S5.

2.4.1. Pre-pandemic vaccination and contact-targeted antiviral prophylaxis

The combined programme of vaccination and TAP demonstrates some desirable features. Plots of illness incidence and antiviral applications as functions of time are shown in figure 3a–c, for varying values of compliance and delay time. For reference, these plots include incidence curves corresponding to the vaccination programme alone, so that the contribution of the TAP protocol is clearly demonstrated. These plots illustrate that the vaccination programme appears to enhance the effects of the reactive strategy:

• —Figure 3a shows that, for short response times, the suppression of epidemic growth rate and delay of peak timing already observed for the TAP protocol are amplified when TAP is carried out in concert with pre-pandemic vaccination. Not only is the effect greater for a delay time of 1 day, but suppression of initial growth is still observed when the delay time is extended to 9 days (figure 3b).
• —Figure 3c demonstrates that, while the suppression of initial growth rate vanishes for long delay times, the illness suppression attributable to TAP is still significant even with a long delay time of 17 days.

The image plots of attack rate and efficiency shown in figure 3d and 3e, respectively, demonstrate a marked departure from the behaviour of the reactive TAP strategy alone. The first significant difference is that the diminishing return on TAP compliance reverses for high compliance and short delay time, producing the desired coincidence of high suppression and efficiency. In addition, for compliance rates below about 60%, both attack rate and efficiency become almost independent of delay time. Both of these differences are positive in the sense that they improve both the ‘best case’ and ‘worst case’ scenarios with respect to delay time. That is, in a situation where logistical delay time is long, a sufficient compliance rate can still generate substantial suppression, with an achievable antiviral stockpile. On the other hand, if the response is fast, a high compliance rate can facilitate both high efficiency and high suppression.

If the delay time is long enough that first-generation effects are limited, the effect of TAP on epidemic peak timing vanishes. Examination of electronic supplementary material, figure S8a shows that this delay time threshold depends on compliance rate, indicating that TAP feeds positively into its own mechanism. That is, high TAP compliance lengthens the first-generation spreading rate, which opens a wider window of response times capable of acting on first-generation transmission events.

The benefits of coupling reactive strategies with pre-pandemic vaccination are not observed for the case of GTAP, which still suffers from the problem of over-distribution of antivirals. Even when applied to the vaccinated population, the strategy requires prohibitively large antiviral stockpiles, and no efficiency gains are observed for high compliance rates.

Even though GTAP distributes many more prophylaxis courses, it has a less pronounced effect on the initial spreading rate of the virus, which translates to an earlier epidemic peak than for TAP (with the same delay time and compliance rate). In addition, the rather modest effect of GTAP on spreading rate does not appear to couple with the slow down provided by pre-pandemic vaccination, while combining TAP with vaccination has a significant combined effect on spreading rate. This difference can only be explained as a result of the targeting method: the contact-targeted protocol is intended to act explicitly on first-generation spreading events, which will hinder the spread of the disease in space, despite the complex connectivity between geographical regions arising from human travel [24,47]. Because GTAP only targets interactions based on residential location, it has no direct pre-emptive effect on the spatial spread of the disease, and is perpetually ‘catching up’ with the virus. A full description of these results, including movies of disease spread during GTAP implementation, is given in electronic supplementary material, figure S6 and movies SM4, SM7 and SM8).

Careful comparison of the movies in the electronic supplementary material reveals a general trend with respect to reactive interventions: for the cases without reactive intervention the movies show smooth, mono-modal prevalence levels within local regions (electronic supplementary material, SM1 and SM2). However, for the scenarios including a reactive intervention (electronic supplementary material, SM3–SM8) we observe more drawn-out prevalence profiles, with locally noisy dynamics (particularly during the ‘tails’ of the epidemics).

2.5. Coupling benefit

Now that we have described the general results for individual and mixed strategies, we turn to a more nuanced analysis of the coupling between static and reactive interventions. To assess the benefits associated with coupling of the reactive prophylaxis strategies and the pre-pandemic vaccination programme, we begin by introducing a simple measure which we call the coupling benefit,

$${\beta }_{ij}={\sigma }_{ij}-({\sigma }_i+{\sigma }_j),$$ 2.2

where σ_ij is the illness suppression computed for the combined strategy, while σ_i and σ_j represent the suppression levels computed for each individual strategy separately. The measure β_ij can be interpreted as the quantitative benefit from combining the component strategies i and j, and allows us to tell whether or not the processes are mutually beneficial. It provides a naive quantification of whether or not ‘the whole is greater than the sum of the parts’, in terms of illness suppression.

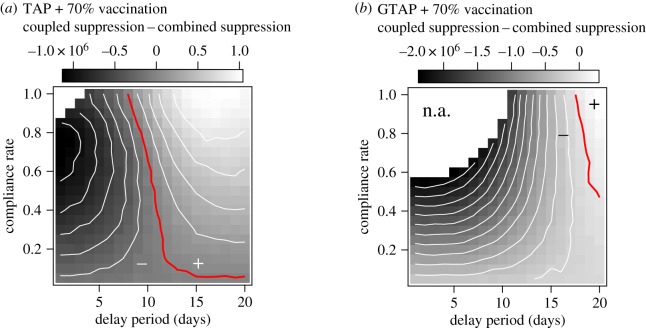
The coupling benefit results for TAP and GTAP combined with pre-pandemic vaccination are plotted in figure 4a and 4b, respectively. The most obvious result of this analysis is that, from a coupling perspective, GTAP does not mix well with pre-pandemic vaccination, while TAP demonstrates positive coupling benefit for large areas of parameter space. The benefits of combining TAP and vaccination are greatest for long delay times and high coverage. In this region, TAP alone has almost no effect on illness levels, because of a strong dependence of suppression on delay time (figure 2d). The positive coupling in this region is apparently due to the slower epidemic growth rate imparted by vaccination. The disease moves through the partially vaccinated population more slowly, allowing even a very late prophylaxis programme to provide protection.

Figure 4.

Image plots of the coupling benefit associated with combining TAP (a) and GTAP (b) with pre-pandemic vaccination at a compliance rate of 70% as functions of delay period and the compliance rate with the specified reactive protocol within targeted groups. Coupled suppression refers to the illness suppression provided by combining reactive antiviral prophylaxis and pre-pandemic vaccination, while combined suppression refers to the sum of the suppression provided by each component strategy taken individually. The blank areas (marked n.a. in (b)) define regions where the combined suppression is greater than the attack rate expected when no intervention is used and the coupling benefit does not provide an intuitive interpretation. The red contours correspond to coupling benefit values of 0, where the suppression provided by the combined strategy is simply the sum of the suppression provided by each separate method.

Interestingly, for the region of parameter space in which the mutual effects on epidemic growth rate are more pronounced (figure 3a), the coupling benefit in terms of attack rate suppression is at a minimum. This is somewhat intuitive in the sense that TAP by itself is reasonably effective in this region (though inefficient), driving down the coupling benefit according to equation (2.2), which depends only on absolute suppression levels. Furthermore, in a crucial region of this parameter space, characterized by high efficiency and low attack rates (figure 3d), the coupling benefit does not provide a useful intuition as the combined suppression (σ_i + σ_j) is larger than I_o, which points to the basic limitation that the sum of σ_i and σ_j is not an attainable quantity in practice. To further our practical understanding of these coupling effects over the whole parameter space, and to account for dose numbers, we must take a more nuanced approach. In the next section, we do this by computing the per-course illness suppression of each method within the combined strategy.

2.6. Component efficiency analysis

Simply comparing attack rates is not sufficient to gain an intuition regarding the coupling process. In order to understand how the component strategies affect one another, we introduce the component efficiency, which is a simple extension of the per-course suppression efficiency introduced in equation (2.1). We wish to quantify the efficiency of each strategy separately, when they are working together. To do so, we compute component efficiency as the average illness suppression attributable to each individual course of measure i included in the mixed protocol ij,

$${\eta }_{(i|ij)}=\frac{I_j-I_{ij}}{c_{(i|ij)}},$$ 2.3

where I_j is the attack rate computed for the mitigation strategy excluding measure i, I_ij is the attack rate computed for the coupled strategy incorporating both programmes i and j, and c_i|ij is the expected number of courses (i.e. vaccines or antiviral courses) of type i applied when the mixed strategy ij is in effect.

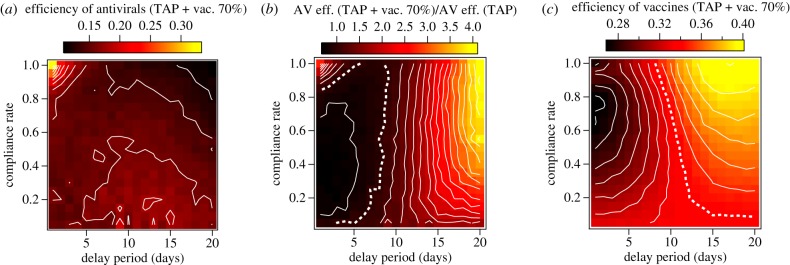
The results of component efficiency analysis for the combination of TAP and pre-pandemic vaccination are shown in figure 5. The efficiency attributable to antivirals is depicted in figure 5a. To quantify the relative increase in efficiency of antivirals when they are combined with vaccination, figure 5b plots the ratio of the TAP component efficiency to that of TAP alone (as plotted in figure 2d). Likewise, the component efficiency of pre-pandemic vaccination is shown in figure 5c, in which the white dotted contour corresponds to the efficiency of vaccination alone.

Figure 5.

Image plots demonstrating component efficiencies determined for the TAP protocol and pre-pandemic vaccination, when they are applied together. (a) The efficiency attributed to antivirals when they are combined with a 70% vaccination programme. (b) The ratio of the component efficiency of antivirals in the combined strategy and the raw efficiency of antivirals in the TAP protocol alone. The dotted white contour in (b) highlights a ratio of 1, where the combination of TAP with vaccination does not change the per-course suppression for antivirals. (c) Illustration of how vaccine efficiency scales with TAP compliance and delay period. The dotted white line highlights a component efficiency value of 0.34, the suppression per vaccine computed for 70% vaccination alone (figure 1).

Component efficiency analysis produces three notable results:

• (i)Vaccination increases the efficiency of antivirals for short delay times and high compliance. This coupling explains the favourable scaling of efficiency with compliance for the short delay times shown in figure 3e. Vaccination efficiency is actually reduced in this area of parameter space, as shown in figure 5c.
• (ii)The area of parameter space characterized by the largest positive coupling values in figure 4a demonstrates enhancement of both antiviral and vaccine efficiency, compared with their independent efficiencies.
• (iii)For fast delay times and compliance rates below approximately 80%, both antivirals and vaccines act with lower efficiencies together than they do separately.

To understand this further, we can express the component efficiency in terms of the coupling benefit,

$${\eta }_{i|ij}=[{\beta }_{ij}+{\sigma }_i]{[c_{i|ij}]}^{-1},$$ 2.4

in which σ_i is the suppression attributed to measure i applied by itself. It follows that, for the efficiency of an individual strategy to increase when combined with another (i.e. η_i|ij > η_i), the following inequality must be satisfied:

$${\beta }_{ij}+{\sigma }_i>{\eta }_i{c}_{i|ij},$$ 2.5

that is, the illness suppression of strategy i acting alone plus the benefit of coupling it with the other strategy must be greater than the linear prediction based on its per-course suppression when applied by itself. Note that for reactive strategies it is possible to have both a negative coupling benefit in terms of absolute illness suppression and an increase in per-course efficiency. On the other hand, for static intervention strategies this is not possible because c_i|ij = c_i, as specified by the homogenous compliance rate, and σ_i is a constant, so the component efficiency is a linear function of coupling benefit (this is clear when comparing figure 5c and figure 4b).

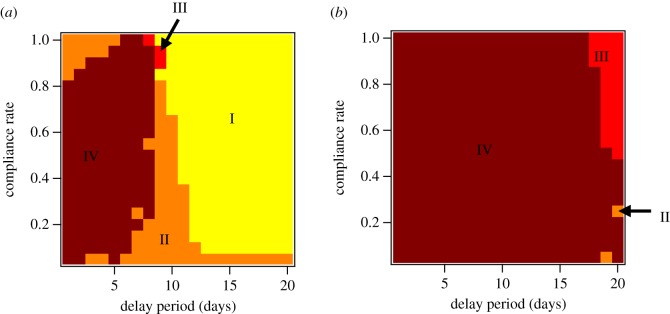
Using this framework, we can define four coupling regimes applicable to reactive strategies for which dose numbers are not constant and suppression is a function of our control parameters:

• —Regime I: [ η_i|ij > η_i ; β_ij > 0 ], in which total suppression is greater than the sum of the parts and per-course suppression increases due to coupling. This is the most favourable regime.
• —Regime II: [ η_i|ij > η_i ; β_ij < 0 ], in which total suppression is less than the sum of its parts, but per-course suppression is still enhanced because of coupling.
• —Regime III: [ η_i|ij < η_i ; β_ij > 0 ], where per-course efficiency is reduced through coupling, but the intervention measures in combination still suppress more illnesses than the sum of their individual contributions.
• —Regime IV: [ η_i|ij < η_i ; β_ij < 0 ], the least favourable regime, in which coupling benefit is negative and per-course suppression is reduced relative to its un-coupled value.

Figure 6 consolidates our understanding of the benefits and drawbacks of coupling antiviral prophylaxis with pre-pandemic vaccination. For the case of contact-targeted distribution (figure 6a), regime I dominates the parameter space, applying to almost all combinations of compliance rate for delay times above 10 days.

Figure 6.

Coupling regime diagrams for antiviral prophylaxis strategies coupled with 70% pre-pandemic vaccination. Regimes I–IV are shown for (a) contact-TAP and (b) GTAP.

Regime II is also prominent, showing that, over a majority of these scenarios, coupling with pre-pandemic vaccination increases the per-course illness suppression of antivirals. For the parts of parameter space in which antivirals alone provide significant benefits (i.e. for short delay times and moderate compliance), per-course efficiency decreases owing to its coupling with pre-pandemic vaccination. This is because coupling between TAP and pre-pandemic vaccination slows the time scale of disease spread substantially (figure 3a,b and electronic supplementary material, figure S8). While illness prevalence is lowered substantially as well, this lengthening of the disease ‘dwell time’ within targeted communities beyond the antiviral dosage period requires additional rounds of prophylaxis, leading to a decline in per-course illness suppression.

In the case of our geographical targeting technique (figure 6b), this effect leads to almost exclusively unfavourable coupling, with regime IV dominating the vast majority of parameter space. This occurs despite the much less pronounced effects of GTAP on the global time scale of disease spread. GTAP targets so many individuals for prophylaxis that the per-course efficiency plummets, even though suppression is substantial.

In the case of the TAP protocol, the dominance of regime I for delay times greater than 10 days deserves some further discussion. There are several factors that must be taken into account in order to explain the counterintuitive result that, in combination with vaccination, antivirals are relatively more efficient with longer delay times (figure 5b). Without a detailed assessment of disease transmission between the individuals and mixing groups in the model, and detailed quantification of the distribution and activity of antivirals, it is not possible to give a thorough analysis of the relevant effects, but we can still make conjecture on a likely explanation.

There are two time scales that are important with respect to the effectiveness of contact-TAP. The first is the time required for the disease to transmit between two subsequent generations, T₂. If the delay time for TAP, T_delay, is longer than T₂, then prophylaxis will not have the intended effect, and will only act incidentally on subsequent rounds of infection that happen to expose the same individuals originally targeted.

The second time scale of interest is the time required for a mixing group to effectively become immune from further introductions of the infection, T*. Assessment of T* would require an in-depth analysis of the simulation results that goes beyond the scope of this work. However, if this time scale T* is longer than T_delay plus the prophylaxis period T_p = 10d, then multiple rounds of prophylaxis will be required on the same targeted subpopulations, and the efficiency of TAP will suffer.

In short, if T_delay > T₂, then prophylaxis will not have the intended effect, and if T* > T_delay + T_p, then prophylaxis will not be efficient. Using these principles we can tentatively explain the dominance of regime I for long delay times as follows.

Figure 3c shows that vaccination has a significant effect on the initial growth rate of the disease, and should therefore increase T₂. However, the same figure also indicates that antiviral prophylaxis with T_delay > 10d does not add to the effect of vaccination on T₂, excluding the possibility that it is having the intended effect on first-generation spreading events. It is also clear that vaccination alone reduces the overall attack rate significantly while also drawing out the epidemic, which could reasonably correspond to a higher likelihood of multiple waves of infection through the same mixing groups. This leaves us to speculate that, in this regime of long delay times, TAP does not act directly on second-generation transmission events, but instead acts indirectly on subsequent waves of transmission. This could produce a reduction in T*, helping to prevent multiple rounds of prophylaxis, and facilitating an efficient TAP programme despite the long delay times.

To validate this conjecture, further analysis would be necessary to quantify the time scales of interest and elucidate the activity of antiviral prophylaxis when delay times are long compared with T₂.

3. Conclusion

To conclude, we conducted a study of pandemic influenza response strategies over a systematic sweep of compliance rates and response times and characterized the disease dynamics within a population of 23 million individual agents representing the Australian population. We then investigated the coupling of different prophylaxis strategies using analytical techniques that are likely to be applicable in other cases involving increasingly complex combinations of reactive intervention methods. Our desire was to decouple the component effects in an effort to understand the complexity underlying disease dynamics in the presence of reactive response methods that modulate contagion properties in space and time. We took initial steps to achieving this by introducing two simple measures to help elucidate how the respective effects combine to mitigate pandemic spread: the first of these was the coupling benefit, which quantifies the difference between illness suppression resulting from coupled strategies and the sum of their respective individual effects. The second was the component efficiency, which quantifies the per-course illness suppression of each component strategy in the combined approach, and allows us to establish to what degree the respective strategies amplify the effects of the others.

By examining these measures as functions of the average compliance rate and the delay time between index case detection and resource deployment, we show that cooperative effects can act on both the severity and time scale of disease spread, leading to nonlinear coupling of the combined methods and substantially widening the time window for effective application of reactive strategies. However, these beneficial effects are highly dependent on the type of contact targeting. While contact-targeted prophylaxis (TAP) performs well over a broad range of parameters, and demonstrates beneficial coupling with vaccination, GTAP performs with prohibitively low efficiency and does not couple well with vaccination.

Our results emphasize the wisdom, well established in the public health community, that pandemic intervention policy needs to take into account the logistical constraints on resource deployment, the expected levels of compliance and case severity [14,34]. Importantly, we identified regimes in which the use of TAP is beneficial and relatively efficient, even when logistical delays are significant and compliance is relatively low. Unfortunately, nowhere in our study did we identify what would be considered successful containment of the pathogen. Even in cases where suppression was very high, the disease still managed to spread between regions and eventually become widely distributed. Furthermore, the more successful our suppression plans, the more drawn-out the epidemic, lengthening the required logistical response to potentially untenable duration. The realistically ‘leaky’ nature of our response plans and the unavoidable problem of asymptomatic index cases are responsible for this divergence from the results of idealized models in which immunization is deterministic and the percolation behaviour of the system can be exploited to great (but apparently unrealistic) effect [8,48,49].

The real-world consequences of influenza pandemics demand data-rich, adaptable modelling approaches for assessments of intervention plans. The sobering nature of our results comes about as a result of realistic social structure, multi-scale mobility, heterogeneous interactions in various settings and logistical constraints, all of which must be taken into account to provide reasonable assessments of projected intervention effectiveness. The work we have presented here is a step forward in understanding the complex, dynamic landscape produced by epidemics and reactive intervention responses.

4. Methods

We performed our simulations using an extension of the AceMod (Australian Census-based Epidemic Model) platform, which was developed by Cliff and co-workers to simulate influenza dynamics in Australia [24,25]. It offers a discrete-time simulation of disease spread among a population of 23 406 335 agents stochastically generated according to distributions from the 2016 comprehensive Australian census. The AceMod platform can be characterized as an agent-based model which incorporates a fine-grained susceptible–exposed–infectious–recovered (SEIR) cycle. Individuals transition from the susceptible to exposed state upon stochastic transmission of the virus from their infected contacts, become ill for a period of several days over which they may transmit the disease to others, and eventually recover, after which they are immune to further infection. In addition to this basic model of influenza disease progression within infected individuals, the approach we take here is underpinned by three important elements:

• (i)An Australian-focused global pandemic scenario, where infected individuals arrive by air and the disease spreads via social mixing groups.
• (ii)A layered social mixing model based on comprehensive commuting data, school attendance data and local residential statistics.
• (iii)Implementation of proposed intervention strategies for containing the pandemic.

The electronic supplementary material, Methods section contains a detailed description of how transmission between agents is computed, and the exact functional form of our disease progression model can be found in the work by Cliff et al. [24].

We assume Australia is exposed to a widespread global pandemic caused by a new strain of influenza that emerged elsewhere. To capture this scenario, our seeding conditions follow the approach outlined by Germann et al. [9], with influenza being introduced continuously to residential areas within 50 km of international airports. This influx to each seeding region is proportional to the number of daily international passengers arriving at the corresponding airport, according to the Australian Bureau of Infrastructure, Transport and Regional Economics (BITRE) [50].

4.1. Social mixing model

The layered social mixing model over which the virus spreads comprises three components to approximate routine interactions between agents: the work, school and community layers. The community layer captures interactions within the home, household cluster and neighbourhood of each agent. Interactions at work or school can spread the disease between localities owing to travel patterns of commuters and students. A schematic of the model is illustrated in electronic supplementary material, figure S1. The spread of the pandemic occurs in alternating daytime and nighttime phases. During the daytime phase agents that attend work or school can interact outside of their local regions. At night, all agents may spread the disease locally.

4.2. Pandemic control measures

We have implemented three mitigation strategies. These include pre-pandemic vaccination and two targeted, dynamically applied antiviral prophylaxis methods. These dynamic strategies are: GTAP, and contact-TAP. In our algorithm, we implemented vaccination and antiviral administration as reductions to the context-dependent force of infection between infected and uninfected agents.

The dynamic interventions are triggered by detection of index cases. In geographical targeting, an index case is the first detected illness (symptomatic infection) in a neighbourhood that is not currently scheduled for intervention. In contact targeting, index cases occur when an ill individual is detected who has close contacts who are not scheduled for antiviral prophylaxis. For the purposes of contact targeting, interactions at home, work and school environments are considered ‘close’. Individuals can be subject to multiple rounds of targeted intervention if new index cases appear after the conclusion of previous rounds, each of which lasts 10 days.

Each new symptomatic infection has a fixed chance to be detected, simulating the individual seeking medical treatment and receiving a positive clinical diagnosis. Detection results in application of the chosen mitigation strategy to the detected individual after a period of 1 day. If the detected individual is determined to be an index case, the strategy is applied to the relevant sub-population of their contacts after a fixed delay time that we systematically vary in order to investigate the effect of logistical roll-out time on pandemic mitigation. The other free parameter we investigate is the average compliance rate, which describes the percentage of the targeted population that is treated during pandemic response. For example, given a compliance rate of 0.5, if a neighbourhood were targeted for GTAP, each of its residents (excluding the index case and any other previously detected cases that subsequently recovered) would have a 50% chance of being treated with antivirals. Agents who have previously become ill and recovered without illness detection occurring could be treated in subsequent rounds of mitigation.

The flow of events, from symptomatic infection of an index case to the end of a single round of intervention, is shown in electronic supplementary material, figure S2. The process begins with detection of an index case.

For the pre-pandemic vaccination strategy, each individual has an independent probability of being vaccinated prior to the onset of the pandemic equal to the vaccine compliance rate. For the dynamic strategies, the compliance rate is equal to the probability that an individual will be treated with the selected measures, given that they are targeted. In the case of mixed interventions, the treatment probabilities are evaluated independently for each applied measure.

Data accessibility

All data and source code can be made available upon request from the authors, subject to any restrictions placed upon release by The University of Sydney during the ongoing software disclosure process. AceMod is registered under The University of Sydney’s invention disclosure CDIP ref. 2019–123.

Authors' contributions

C.Z., K.M.F. and M.P. designed the research; K.M.F. and C.Z. wrote the software, performed the simulations and analysed the data; C.Z., N.H., K.M.F. and M.P. interpreted the data and wrote the manuscript.

Competing interests

We declare we have no competing interest.

Funding

This work was supported by the Australian Research Council Discovery Project (grant no. DP160102742).