Factors affecting optic nerve head biomechanics in a rat model of glaucoma

Abstract

Glaucoma is the leading cause of irreversible blindness and is characterized by the death of retinal ganglion cells, which carry vision information from the retina to the brain. Although it is well accepted that biomechanics is an important part of the glaucomatous disease process, the mechanisms by which biomechanical insult, usually due to elevated intraocular pressure (IOP), leads to retinal ganglion cell death are not understood. Rat models of glaucoma afford an opportunity for learning more about these mechanisms, but the biomechanics of the rat optic nerve head (ONH), a primary region of damage in glaucoma, are only just beginning to be characterized. In a previous study, we built finite-element models with individual-specific rat ONH geometries. Here, we developed a parametrized model of the rat ONH and used it to perform a sensitivity study to determine the influence that six geometric parameters and 13 tissue material properties have on rat optic nerve biomechanical strains due to IOP elevation. Strain magnitudes and patterns in the parametrized model generally matched those from individual-specific models, suggesting that the parametrized model sufficiently approximated rat ONH anatomy. Similar to previous studies in human eyes, we found that scleral properties were highly influential: the six parameters with highest influence on optic nerve strains were optic nerve stiffness, IOP, scleral thickness, the degree of alignment of scleral collagen fibres, scleral ground substance stiffness and the scleral collagen fibre uncrimping coefficient. We conclude that a parametrized modelling strategy is an efficient approach that allows insight into rat ONH biomechanics. Further, scleral properties are important influences on rat ONH biomechanics, and additional efforts should be made to better characterize rat scleral collagen fibre organization.

1. Background

Glaucoma is the leading cause of irreversible blindness, with an estimated 76 million cases worldwide [1]. Blindness in glaucoma is due to the dysfunction and loss of retinal ganglion cell axons, the conduits by which vision information is sent from the retina to the brain. Current therapies for glaucoma are all focused on lowering intraocular pressure (IOP), as elevated IOP is a causative risk factor for glaucomatous optic neuropathy. Unfortunately, these therapies are not always effective [2,3], and the development of novel therapies is made difficult by the current lack of understanding of glaucoma pathophysiology. In particular, it is not known how biomechanical insult to the optic nerve head (ONH), widely accepted as a key aspect of glaucoma pathophysiology [4,5], affects the apoptosis of retinal ganglion cells. Research to date indicates that the answer is highly complex; remodelling, alteration of cell behaviour, decrease in ONH blood flow and blockage of retinal ganglion cell axonal transport may all result from increased mechanical stress and strain in the ONH [5–7].

Rodent glaucoma models provide an opportunity to learn more about the role of biomechanics in glaucoma pathophysiology because of their low cost, ease of animal husbandry and low genetic variability between individuals when compared with non-human primates [7]. These characteristics make them appropriate for use in mechanistic studies requiring high numbers of subjects. Further, the rat has benefits for biomechanics studies over the mouse due to its larger eye size, which makes its tissues easier to handle for biomechanical testing. In addition, rat ocular hypertensive models present with important characteristics of human glaucoma, and rat models of both acute and chronic IOP elevation exist, allowing early and late events in the disease process to be studied [7–9].

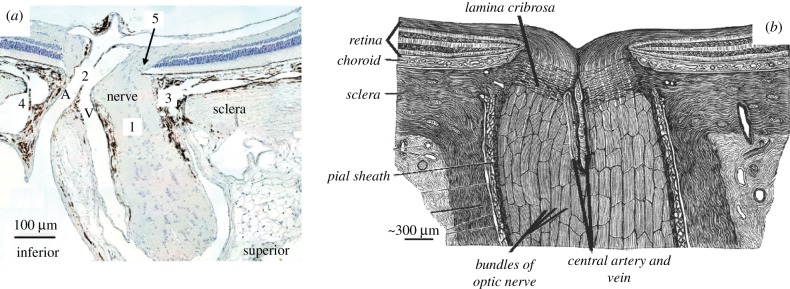
However, there are anatomical differences between the rat and human ONH that result in different ONH biomechanical environments [10,11]. Specifically, there are five key anatomical differences [7,12] that are expected to impact ONH biomechanics (figure 1), as follows. (1) The rat does not have a connective tissue lamina cribrosa within its scleral canal. (2) Rather than passing through the centre of the nerve at the level of the scleral canal as in the human, the central retinal artery (CRA) and vein (CRV) pass through the sclera on the inferior side of the nerve in the rat. (3) The rat contains a vascular plexus, referred to as the perineural vascular plexus, between the optic nerve and scleral canal wall (primarily on the superior side of the nerve). Thus, the scleral canal in the rat is sometimes referred to as the neurovascular scleral canal [12]. (4) An additional canal, the inferior arterial canal, inferior to the neurovascular scleral canal, exists in the rat sclera. The so-called scleral sling separates the inferior arterial canal from the neurovascular scleral canal, and the CRA (along with other vessels) passes through the inferior arterial canal. (5) Bruch's membrane (BM) extends towards the nerve axis from the superior side of the nerve in the rat, creating a superior BM ‘overhang’ around which retinal ganglion cell axons are forced to pass.

Figure 1.

Histologic section of the rat (a) and schematic drawing of the human (b) ONH. The anatomical differences between the two species are displayed, including five key differences of note (numbered 1–5) as described in the text. A, central retinal artery; V, central retinal vein. Adapted from The Journal of Biomechanical Engineering [10].

Our previous studies are the only ones that have focused on characterizing rat ONH biomechanics to date [10,11]. The goal of these studies was to determine stress and strain in individual-specific rat ONH geometries using computational modelling. However, individual-specific modelling is a time-intensive process, and thus cannot be used effectively to fully explore how anatomical variation affects ONH response to elevated IOP.

Therefore, the purpose of this study was to conduct a sensitivity analysis to determine how variation in tissue material properties and anatomical features affect rat ONH biomechanics. To do so, we developed a rat ONH finite-element model with parametrized geometry. Using Latin hypercube sampling (LHS), we varied six geometric parameters, 13 tissue material properties and IOP to create nearly 1200 rat ONH model variants. A partial rank correlation coefficient approach was used to rank the sensitivity of two outcome measures, namely 95th percentile first principal strain and 5th percentile third principal strain in the anterior optic nerve, to changes in the studied parameters. The results from this study will guide future rat ONH modelling studies and provide biomechanical context for interpreting results from rat glaucoma studies with the ultimate goal of understanding the role of biomechanical insult in retinal ganglion cell pathophysiology.

2. Methods

2.1. Model geometry

2.1.1. Approach overview

Sensitivity studies in which geometric parameters are varied are especially difficult because they require the generation and meshing of many model geometries. Thus, they are infeasible unless the process is automated. We therefore developed a custom Python script to build and mesh rat ONH geometries in Trelis (v. 16.5, Computational Simulation Software LLC, American Fork, UT, USA), given a set of geometric input parameters. Model geometry variants were generated by varying input parameters about a baseline model and were informed from measurements made on seven individual-specific rat ONH geometries used in a previous modelling study [11]. Unlike previous studies on the human ONH, we could not assume axisymmetry. Thus, to capture complex ONH tissue anatomy, we lofted volumes through tissue cross-sections represented by geometric primitives such as ellipses. Finally, a series of Boolean operations were used to produce the finalized geometry for each model.

2.1.2. Measurements

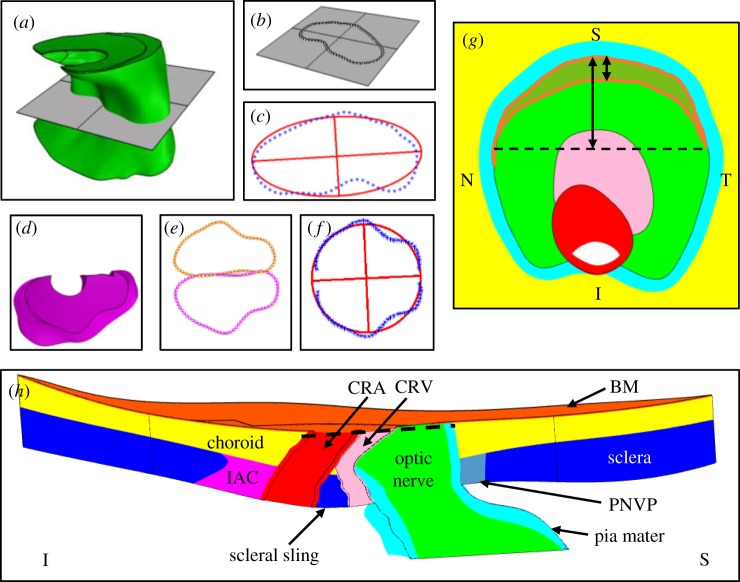
To obtain information needed for parametrized geometry development, we measured key tissues from seven previously developed, specimen-specific rat ONH model geometries, whose construction has been detailed elsewhere [11]. In brief, rat eyes were perfusion-fixed at approximately 10 mm Hg. Serial sections of the rat ONH were stained and imaged following an established three-dimensional (3D) histomorphometric technique [12–14]. Manual delineations were performed within digital 3D reconstructions to create point clouds of the ONH structures. Then, we used computer-aided design software (Rhino v. 5 SR 14, Robert McNeel and Associates, Seattle, WA, USA) to manually generate tissue volumes from these point clouds.

In the current study, we took measurements from these tissue volumes using Rhino and custom MATLAB (2017a; Mathworks, Natick, MA, USA) scripts, as described below. This provided the range of dimensions for ONH geometries in our sensitivity study. In the following, all surfaces are non-uniform-rational basis spline surfaces and all curves are Bezier curves.

The cross-sectional shapes of key tissues in the ONH were assessed at three reference surfaces: BM, the anterior scleral surface and the posterior scleral surface. Measured tissues included the optic nerve, the CRA and the CRV. Rhino was used to fit a curve to the intersection of a tissue boundary and a given reference surface. A group of 72 equally spaced points were placed along the curve length. A plane was fit through these points, and the intersection curve and the points were projected to the plane (figure 2). Using a script from the MATLAB file exchange [15], an ellipse was fit to the projected points. The centroid of the projected intersection curve, and the major and minor axes of the ellipse were recorded. The same process was repeated to assess several tissue ‘openings’: BM opening, the anterior scleral canal opening and the posterior scleral canal opening.

Figure 2.

Examples of measurements made on an individual-specific rat ONH geometry. (a–c) Ellipse fitting of the optic nerve cross-section at the posterior scleral canal opening plane. (a) The posterior scleral canal opening plane passing through the optic nerve. (b) Intersection curve with points overlaid. (c) Ellipse (red) fit through the points (blue). (d,e) Ellipse fitting of the inferior arterial canal cross-section at the anterior scleral surface. (d) Top-down (looking from anterior to posterior) view of the inferior arterial canal. (e) Cross-section points of the inferior arterial canal at the anterior scleral surface (magenta) and mirrored points (orange). (f) Ellipse fit through subsets of the inferior arterial canal cross-section points and mirrored points. (g) En face view of the optic nerve with BM hidden. The BM overhang region is outlined in orange. Arrows indicate measurements made to characterize the BM overhang. (h) Superior–inferior cut plane view of the entire individual-specific model for reference. The dashed line in (h) indicates the cut plane being viewed in (g). S, superior; I, inferior; N, nasal; T, temporal; BM, Bruch's membrane; CRA, central retinal artery; CRV, central retinal vein; IAC, inferior arterial canal; PNVP, perineural vascular plexus. Tissue colours: optic nerve (green), BM (orange), choroid (yellow), sclera (blue), pia mater (cyan), CRV (pink), CRA (red), perineural vascular plexus (grey), inferior arterial canal (magenta).

The measurement method described above was slightly modified in several instances. Specifically, the inferior arterial canal openings have shapes similar to semi-ellipses. Therefore, the projected points representing an inferior arterial canal opening shape were first mirrored about an axis coincident with the superior side of the projected inferior arterial canal opening curve, and then an ellipse was fit to these points (figure 2). Half of the resulting ellipse was taken as the shape of the given inferior arterial canal opening. Additionally, since the optic nerve boundary is not directly intersected by the sclera, the optic nerve cross-section was assessed by finding the intersection between the nerve boundary and a plane fit through each scleral canal opening boundary.

The CRV has two branches that emanate from the main lumen and travel in the inferior direction towards the inferior arterial canal across the anterior scleral surface. The CRV cross-section near the anterior scleral surface was always measured just posterior to these branches. To obtain information about the optic nerve posterior to the scleral surface, the posterior scleral canal opening plane was offset approximately 75 µm posterior to the posterior scleral canal opening, and this offset plane was then intersected with the nerve boundary. Finally, although the BM opening centroid was recorded as described above, we found that representing BM opening as an ellipse was problematic for meshing the resulting models because such models often had very thin regions (sliver geometries) on the temporal and nasal sides of the nerve, where the BM opening cross-sectional boundary intersected the nerve cross-sectional boundary at a very shallow angle. Therefore, we instead took measurements of the BM overhang, measuring the distance between the superior edge of the nerve cross-section and the inferior edge of the BM overhang along the superior–inferior axis (figure 2). We also found the locations of the points at the nasal and temporal sides of the nerve–BM cross-section at which the BM overhang ended.

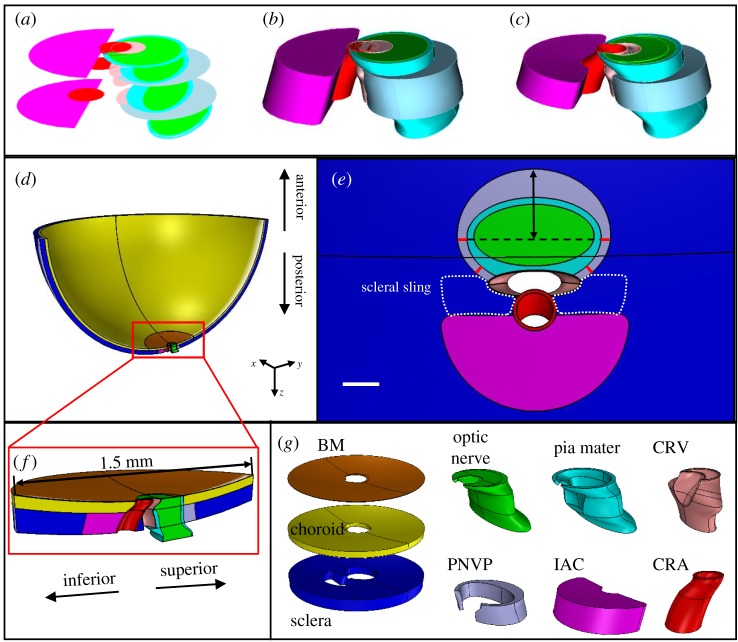
2.1.3. Generating the model geometry

We developed a custom Python script to generate and mesh rat ONH geometries using Trelis. The parametrized model consisted of the posterior eye, represented by a semi-spherical shell split into two regions: a peripheral region that extended to the eye equator and a peripapillary (near the ONH) region that contained the ONH and surrounding tissues. To be comparable with our previous modelling [11], the peripapillary region was a disc of 1.5 mm diameter. The peripheral region consisted of two layers, namely the choroid and the sclera, with the following dimensions derived from the literature: outer radius = 3.375 mm [16], sclera thickness = 0.105 mm and choroidal thickness = 0.055 mm [12]. The axis of the shell was aligned with the BM opening centroid and the z-axis, where the z-axis pointed in the posterior direction, the y-axis pointed in the superior direction and the x-axis pointed in the temporal direction. Although the model was fully 3D, we built it such that it was symmetric about the y–z plane (i.e. the superior–posterior plane). The following features were included in the peripapillary region of the model: BM, the choroid, the sclera, the optic nerve, the pia mater, the CRV, the CRA, the perineural vascular plexus and the inferior arterial canal.

We did not include retinal tissue in the model for several reasons. First, the digital reconstructions from which we obtained rat ONH geometry provided only incomplete information on retinal geometry, and it would have been very challenging to estimate the correct paths of the CRA and CRV within the retina. Second, the retina is very soft (i.e. has a low stiffness) and we did not expect it to significantly influence the biomechanical environment in the region of interest, namely optic nerve tissue at and posterior to the level of BM.

To generate the model geometry, the following strategy was used (figure 3). First, a hemispherical shell was generated and split into layers. Specifically, the peripheral region was split into two layers (the sclera and the choroid), while the peripapillary region was split into three layers: the sclera, the choroid and BM. Note that the choroidal thickness in the peripapillary region was equal to the peripheral choroid thickness minus the BM thickness. For example, choroidal thickness was 0.052 mm in the baseline model. For all other tissues, a series of cross-sectional shapes were generated based on average values from tissue cross-section measurements. Each tissue cross-section was placed such that its centroid lay on the y–z (superior–posterior) plane and the z location was approximately concurrent with the appropriate tissue surface. The y location was defined based on the measured x–y distance from the BM opening centroid. Once the entire set of cross-sections for a given tissue was correctly positioned, a loft operation was performed, resulting in an initial tissue volume. A series of Boolean operations between the volumes was then performed to produce the final model geometry. For example, the CRA volume was subtracted from the CRV volume and then the CRV lumen was subtracted from the CRV volume to produce the CRV wall. The thicknesses of the CRA wall, the CRV wall, the BM and the pia mater posterior to the sclera were set at 10, 3, 3, and 10 µm, respectively [10]. Lastly, the perineural vascular plexus filled the space between the pia mater and the scleral canal wall.

Figure 3.

Baseline model geometry. (a) Generating cross-section shapes for the optic nerve, pia mater, perineural vascular plexus (scleral canal opening), CRV, CRA and inferior arterial canal. (b) Initial lofts through the cross-sections. (c) Final volumes after Boolean operations. Minor differences in colour between (a–c) are due to limitations of the display software. (d) Superior–inferior cut view of the entire model. (e) En face view of tissues with all sections anterior and posterior to the sclera hidden. Red lines indicate where the perineural vascular plexus thickness was held constant. The double-headed arrow indicates the dimension of the perineural vascular plexus (scleral canal opening) that was varied in the sensitivity analysis. Dotted white line indicates approximate outline of the scleral sling. Scale bar is 100 µm. (f) Superior–inferior cut view of the peripapillary region of the model. (g) Final geometries of tissues within the peripapillary region. Tissues shown in g are not precisely to scale. All tissue colours are the same as in figure 2. BM, Bruch's membrane; PNVP, perineural vascular plexus; IAC, inferior arterial canal; CRV, central retinal vein; CRA, central retinal artery.

Several other modelling decisions are worth mentioning. First, we ensured that the space between the optic nerve and CRV was always filled with pia mater tissue. This was accomplished by editing the inferior half of the pia mater cross-section within the choroid and sclera to intersect with the CRV central axis. In addition, allowing the shape of the scleral canal openings, and thus the shape of the perineural vascular plexus, to vary often resulted in a poor-quality mesh. Therefore, we assumed that the thickness of the perineural vascular plexus tissue surrounding the inferior pia mater was always 25 µm, based on measurements we made (figure 3). However, the distance between the optic nerve centroid and superior scleral canal opening apex was still allowed to vary in the sensitivity analysis. In addition, as opposed to our individual-specific models [10], the CRV branches were not included in the CRV geometry. Finally, the shapes and sizes of the anterior (at the anterior sclera) and posterior (at the posterior sclera) inferior arterial canal openings were assumed to be equivalent, and the same assumption was made for the anterior scleral canal opening and posterior scleral canal opening.

2.2. Finite-element modelling details

2.2.1. Mesh

The model was meshed with a combination of four-node tetrahedral, six-node prism and eight-node hexahedral elements (electronic supplementary material, figure S2). Prism elements were used to mesh BM, and tetrahedral elements were used to mesh other tissues in the peripapillary region due to their complex shapes. The peripheral region was meshed with hexahedral elements. The peripheral region of the baseline model (see below) was meshed at approximately the same density (156 723 nodes) as was deemed sufficient by a mesh density study completed in our previous individual-specific models (175 000 nodes) [10,11]. Slightly fewer nodes were required because the parametrized model did not contain as much ‘sliver’ geometry as the individual-specific models, and because we chose not to include as much of the posterior nerve and pia mater in order to save computational resources. The peripheral shell was meshed with the same density (57 344 nodes) as the comparable region of the generic posterior eye model used in our previous study [11].

2.2.2. Loads and boundary conditions

We used the ‘relative displacement’ method to account for the effects of prestress in our models [17], since the measurements of ONH geometry were made from ONHs that had been perfusion-fixed at a non-zero IOP. As previously described [10,11], the pressures applied in the model (IOP, CRA blood pressure and CRV blood pressure) were ramped up in two steps. The first step brought the model to the stress state it would have experienced at perfusion fixation, i.e. IOP was increased from 0 to 10 mm Hg, CRV blood pressure was increased from 0 to 10 mm Hg and CRA blood pressure was increased from 0 to 40 mm Hg. The resulting state of the model was taken as the reference for all strain calculations. In the second loading step, CRA blood pressure was increased from 40 to 110 mm Hg, CRV blood pressure was increased from 10 to 30 mm Hg and the magnitude of IOP increase was varied in the sensitivity analysis.

Boundary conditions were applied to the farthest anterior surface of the peripheral model region (at the eye equator). All nodes on this surface were fixed in the z direction, nodes lying on the x–z plane were fixed in the y direction, and nodes lying on the y–z plane were fixed in the x direction (electronic supplementary material, figure S2). This had the effect of allowing nodes on this surface to move in the radial direction but not in the z or circumferential directions, i.e. to allow radial expansion of the equator, but no twisting or axial translation.

We did not apply boundary conditions to the distal optic nerve, i.e. it was unconstrained, similar to previous modelling studies on the human ONH. In vivo, there is slack in the nerve (except at extremes of ad/ab-duction [18–21], and thus we do not expect that the nerve itself will affect ONH strains when the eye is not at extremes of horizontal rotation.

2.2.3. Constraints

We used tied constraints to join the non-conforming meshes between the peripheral region and the peripapillary region at their interface. We also applied a sliding contact without friction between the inferior and superior surfaces within the CRV in case these surfaces interacted due to the bending of the CRA around the scleral sling. We note that we manually examined a subset of 10 models, picking those especially likely to incur contact due to a thin choroidal thickness. We only observed contact in one case. Therefore, we concluded that contact was not a common problem.

2.3. Tissue material models

The tissue material models for all tissues were the same as in our previous individual-specific modelling study [11]. Briefly, the sclera was represented as an isotropic matrix (Mooney–Rivlin solid) reinforced by collagen fibres [22]. The strain energy density function for the sclera was given by

$$W_{\mathrm{sclera}}=W_{\mathrm{gs}}+\hspace{0.17em}{W}_{\mathrm{fibre}},$$ 2.1

where W_gs is the contribution of the ground substance and W_fibre is the contribution of the collagen fibres based on the following relationships:

$$W_{\mathrm{gs}}=c_1(I_1-3)+c_2(I_2-3)+\frac{K}{2}{(\ln J)}^2$$ 2.2

and

$$W_{\mathrm{fibre}}={\int }_{{\theta }_p-\pi /2}^{{\theta }_p+\pi /2}P(\theta )F_2(\lambda [\theta ])\text{d}\theta ,$$ 2.3

where $c_1$ and $c_2$ are the first and second Mooney–Rivlin constants and control the ground substance stiffness, K is the ground substance bulk modulus, $I_1$ and $I_2$ are the first and second invariants of the right Cauchy–Green deformation tensor and J is the determinant of the deformation gradient tensor. In all models, we set c₂ = 0 MPa and K = 1 GPa to be consistent with previous work done on the monkey as well as our own work done on the rat [11,23]. Note that since collagen fibres do not provide resistance to compressive loads, all resistance to compression is provided by the ground substance. Thus, since $c_2=0$, $c_1$ plays a large role in dictating scleral compressive stiffness. $P(\theta )$ is the distribution function of the collagen fibres which lay within a defined material plane, and ${\theta }_p$ is the preferred fibre orientation. The material axes of the sclera were defined element by element such that all fibres lay tangent to the scleral surface, a value of ${\theta }_p=0^{\circ }$ resulted in a circumferential preferred fibre direction, and a value of ${\theta }_p={90}^{\circ }$ resulted in a meridional preferred fibre direction. We assumed that the fibre directions followed the semicircular von Mises fibre distribution which is given by

$$P(\theta )=\frac{1}{\pi I_0(k_f)}\text{exp}\left[k_f\cos (2(\theta -{\theta }_p))\right],$$ 2.4

where $I_0$ is the modified Bessel function of the first kind of order 0 and $k_f$ is the fibre concentration factor. Setting $k_f=0$ resulted in isotropic fibre orientation within the material plane and $k_f=\mathrm{\infty }$ resulted in all fibres being oriented along the preferred direction. In (2.3), $F_2(\lambda [\theta ])$ represents the response of the collagen fibres as defined by

$$F_2(\lambda )=\{\begin{array}{cc}0\hspace{0.17em}& \lambda \le 1\hspace{0.17em}\hspace{0.17em}\\ c_3({\text{e}}^{c_4(\lambda -1)}(\text{Ei}(c_4\lambda )-\text{Ei}(c_4))-\ln \lambda )\hspace{0.17em}\hspace{0.17em}& 1<\lambda <{\lambda }_m\end{array}$$ 2.5

where $c_3$ is the exponential fibre stress coefficient, $c_4$ is the fibre uncrimping coefficient, $\text{Ei}(\cdot )$ is the exponential integral function, $\lambda$ is the fibre stretch and ${\lambda }_m$ is the fibre stretch for straightened fibres. Since previous data showed that the rat sclera behaves nonlinearly in the IOP range of 3–30 mm Hg [24], we assumed that the collagen fibres never fully straightened (λ < λ_m).

All scleral tissue shared the same values of $c_1$ through $c_4$. However, the peripapillary sclera was subdivided into two regions: a peripapillary sclera region proper and a scleral sling region. This approach allowed us to specify fibre organization in a region-specific manner. In all model iterations, we set $k_f=0$ in the peripheral sclera and varied the common $k_f$ value that was shared by the peripapillary sclera and scleral sling. Within the peripapillary sclera proper, we set ${\theta }_p=0^{\circ }$, since our previous inverse modelling study had found that fibres in the peripapillary sclera were oriented circumferentially on average (electronic supplementary material, figure S3) [11]. Within the scleral sling, all fibres were oriented in the x direction (along the sling axis) based on a polarized light microscopy image kindly provided by Dr Ian Sigal as well as images from the literature [25].

All other tissues were modelled as isotropic Mooney–Rivlin solids. However, as was the case for the sclera ground substance, we set $c_2=0$, meaning that these tissues behaved as neo-Hookean solids. We used the Mooney–Rivlin formulation with $c_2=0$ rather than a neo-Hookean formulation because an uncoupled form of the Mooney–Rivlin strain energy density function is implemented in FEBio, making it more suitable for modelling near-incompressible behaviour than the neo-Hookean model, which uses a coupled strain energy density function [26]. In addition, when uncoupled strain energy density functions are used, FEBio implements a three-field element formulation in hexahedral elements which helps to prevent element locking [26,27]. To simplify comparison with previous work, the material parameters of the non-scleral tissues were converted from $c_1$ and K to Young's modulus, E, and Poisson's ratio, $\nu$. All were considered nearly incompressible ($\nu =0.49$) except for the perineural vascular plexus, inferior arterial canal and choroid, whose $\nu$ values were included as parameters in the sensitivity study (see below). All of their Young's moduli values, E, were also varied in the sensitivity study.

2.4. Sensitivity study

2.4.1. Parameters

We varied a combination of parameters dictating model geometry, tissue material properties and IOP in our sensitivity study (table 1). The baseline values for all parameters were selected either from our own data or to be consistent with values used in our previous individual-specific modelling studies, which in turn were taken from the literature [10,11]. The ranges of values were chosen to be consistent with previous sensitivity studies on human ONH biomechanics [28,29].

Table 1.

Sensitivity study parameter ranges. IOP, intraocular pressure; BM, Bruch's membrane; PNVP, perineural vascular plexus; SCO, scleral canal opening; IAC, inferior arterial canal.

name	units	baseline	low	high
choroid thickness	mm	0.055	0.044	0.066
sclera thickness	mm	0.105	0.084	0.126
SCO superior radius	mm	0.33	0.264	0.396
anterior pia thickness	mm	0.02	0.016	0.024
IAC opening area	mm2	0.107	0.064	0.150
eye radius	mm	3.375	2.7	4.05
IOP	mm Hg	25	20	30
sclera c1	MPa	0.035	0.014	0.056
sclera c3	MPa	0.0015	0.0006	0.0024
sclera c4		330	264	396
sclera kf		3.75	1.5	6
BM E	MPa	7	2.8	11.2
pia E	MPa	3	1.2	4.8
choroid E	MPa	0.1	0.04	0.16
PNVP E	MPa	0.1	0.04	0.16
IAC E	MPa	0.1	0.04	0.16
nerve E	MPa	0.03	0.012	0.048
PNVP v	MPa	0.445	0.4005	0.4895
choroid v	MPa	0.445	0.4005	0.4895
IAC v	MPa	0.445	0.4005	0.4895

In more detail, the baseline values of all geometry parameters were derived from our own measurements described above except for eye radius [16] and the thickness of the sclera and choroid [12], which were taken from the literature. All geometry parameters were varied by ±20% from their baseline value [28,29], except for inferior arterial canal opening area which was varied by ±40%, corresponding approximately to a ±20% variation in inferior arterial canal opening radius.

Baseline Young's modulus values for pia mater, optic nerve, CRA and CRV were selected from previous modelling studies on the human ONH [29–32]. For BM and the choroid, we assumed values from the literature [33–36]. We assumed that the perineural vascular plexus and tissue within the inferior arterial canal had the same material properties as the choroid, as they are all highly vascularized tissues. Scleral material properties were informed by our previous inverse finite-element modelling study on the rat sclera [11]. Note that only the scleral material properties were specific to the rat; all other tissue material property values from the literature were from other species.

All material properties were varied ±60% from baseline values [28] with the exception of values for $c_4$ and Poisson's ratio, $\nu$. The range for $c_4$ was chosen as ±20% because it appears in the exponent of the strain energy density function that dictates fibre behaviour. Thus, changes in this parameter had a proportionately larger effect than changes in other parameters [22,28]. We varied $\nu$ in tissues that are highly vascularized (e.g. perineural vascular plexus, inferior arterial canal and choroid [37]), i.e. contain a relatively large amount of blood compared to other tissues, and which thus may not adhere to the typical incompressibility assumption for soft tissues. To be consistent with previous studies [28,29], $\nu$ in these tissues was varied by ±10% about a baseline value of 0.445. The baseline values for sclera $c_1$, $c_3$, $c_4$ were near the average values retrieved in our previous inverse finite-element modelling study [11]. However, we chose to set the baseline $k_f$ value to be lower than the average for the peripapillary sclera obtained in that study. The peripapillary $k_f$ values from that study spanned a wide range, but we were most interested in how $k_f$ affected the ONH when varied from low alignment to moderate or high alignment. In addition, as discussed in more detail elsewhere [11], a previous study measuring fibre alignment in rat eyes using small angle light scattering reported much lower levels of alignment than was found by our inverse method [38]. Therefore, we picked a baseline $k_f$ value such that the range of $k_f$ would encompass values on the lower end of what was found by our inverse method. Lastly, IOP was varied from 20 to 30 mm Hg because in our experience, this range spans the range of IOP levels in brown Norway rats, considering both normal physiology and chronic experimentally induced ocular hypertension (glaucoma).

2.4.2. Latin hypercube sampling

LHS was chosen to explore the parameter space of the ONH model [39,40]. LHS is a stratified Monte Carlo sampling method designed to efficiently sample the entire range of each parameter. This is accomplished by dividing parameter ranges into a user-defined number of bins and randomly assigning parameter values within each bin. The user is also given the option to define the shape of the sampled probability distribution for each parameter. We assumed that all parameters followed uniform distributions [28] and divided parameter ranges into 50 bins. LHS iterations were completed until the standard deviation of both outcome measures (see below) converged. A small and unchanging value of each standard deviation implied that our outcome measure was stable (electronic supplementary material, figure S1). All simulations were run using the solver FEBio (v. 2.9.0) [26].

2.4.3. Outcome measures and parameter ranking

The computed strains for each element were weighted by element volume and mesh density to prevent biasing results. In brief, raw computed strains were weighted following a previously described method to determine the strain distribution in the tissue region and calculated the 95th, 50th and 5th percentiles weighted by element volume [41,42]. We assessed the 95th percentile first principal strain and 5th percentile third principal strain in the anterior optic nerve, defined as the nerve tissue anterior to the posterior scleral canal opening. We focused on these extreme values of strain because they are most likely to induce a mechanobiological response. However, the 95th and 5th percentile values were chosen rather than the 100th and 0th values in order to reduce the influence of numerical artefacts as well as avoid bias from very small regions that have little physiological significance [31,43].

To determine outcome measure sensitivity to parameter variation, a partial rank correlation coefficient (PRCC) approach was used [28]. Briefly, a correlation coefficient in the range −1 (strong inverse correlation) to 1 (strong positive correlation) was calculated for each outcome measure with respect to each parameter. The correlation magnitudes for each parameter were then ranked for our outcome measures: each parameter was assigned a rank from 1 (weakest correlation) to 20 (strongest correlation) with respect to each outcome measure. The ranks were summed across outcome measure and normalized by the highest possible value, i.e. by 40. The resulting ‘cumulative influence factor’ value represented the relative influence of each parameter on both outcome measures. The analysis also produces a p-value that gives the significance of correlation between each parameter and each output factor (table 2). We used a Bonferonni correction to account for multiple comparisons with 20 input parameters, i.e. the threshold significance level was $\alpha =0.05\hspace{0.17em}/20=0.0025$.

Table 2.

Significance (p-values) for correlations between input parameters and the two outcome measures, 95th percentile first principal strain and 5th percentile third principal strain. The threshold for significance was taken as 2.50 × 10⁻³ after Bonferroni's correction (see text). IOP, intraocular pressure, BM, Bruch's membrane; PNVP, perineural vascular plexus; SCO, scleral canal opening; IAC, inferior arterial canal.

parameter	95th percentile first principal strain	5th percentile third principal strain	parameter	95th percentile first principal strain	5th percentile third principal strain
nerve E	0.00a	0.00a	sclera c3	3.60 × 10−2	1.64 × 10−3a
IOP	0.00a	0.00a	choroid E	3.51 × 10−2	5.24 × 10−3
sclera thickness	5.24 × 10−147a	2.07 × 10−138a	choroid v	1.30 × 10−2	1.45 × 10−1
sclera kf	1.26 × 10−17a	1.01 × 10−22a	IAC opening area	7.75 × 10−2	5.17 × 10−2
sclera c1	1.38 × 10−10a	9.97 × 10−14a	SCO superior radius	1.21 × 10−3a	4.80 × 10−1
sclera c4	2.42 × 10−15a	7.38 × 10−13a	anterior pia thickness	3.77 × 10−2	1.53 × 10−1
pia E	5.11 × 10−4a	1.55 × 10−5a	PNVP E	6.71 × 10−1	6.28 × 10−5a
eye radius	3.59 × 10−8a	2.09 × 10−4a	BM E	5.06 × 10−1	4.37 × 10−1
choroid thickness	2.57 × 10−1	3.77 × 10−6a	IAC E	6.89 × 10−1	3.94 × 10−1
PNVP v	1.78 × 10−1	7.79 × 10−6a	IAC v	6.43 × 10−1	4.68 × 10−1

^aSignificant correlations.

3. Results

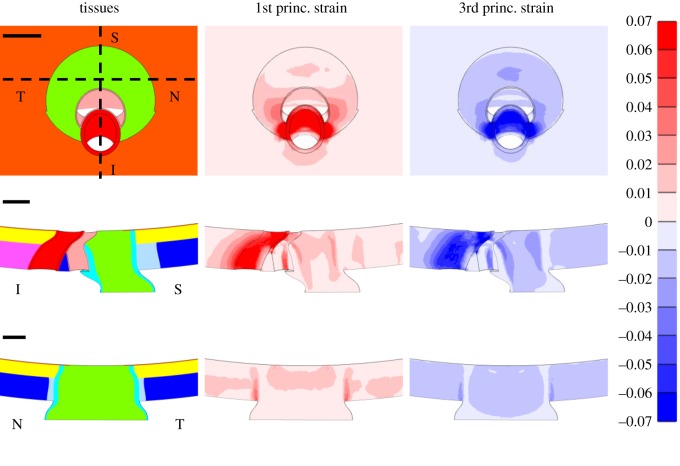
Across all models, the 95th percentile first principal strain values ranged from 1.7 to 7.6%, with a median of 2.5%, while the 5th percentile third principal strain values ranged from −1.5 to −8.2%, with a median of −2.9%. These models demonstrate a large range of strains experienced in the anterior optic nerve based on ONH, geometry, material properties and IOP. The baseline model, in which IOP was raised to 25 mm Hg, had a 95th percentile first principal strain of 2.4% and 5th percentile third principal strain of −2.8% (figure 4). In order to provide a better comparison with values from our individual-specific modelling study [11], we also solved the baseline model after applying an IOP of 30 mm Hg, resulting in a 95th percentile first principal strain of 3.0% and a 5th percentile third principal strain of −3.6%. The ranges observed in the individual-specific modelling study were 3.1–3.7% for 95th percentile first principal strain and −3.5% to −4.2% for 5th percentile third principal strain, and thus our parametrized models were generally consistent with individual-specific modelling results.

Figure 4.

First and third principal strains in the baseline model at an IOP of 25 mm Hg. The en face view (top row), superior (S)–inferior (I) slice (middle row) and nasal (N)–temporal (T) slice (bottom row) are shown. Scale bars shown in the left column are all 100 µm. The superior–inferior and nasal–temporal slices are indicated by the dashed lines in the en face view displaying the model tissues. Tissue colours are the same as in figure 2. The undeformed configuration is shown in all images to ensure that a consistent slice through the model is shown across columns.

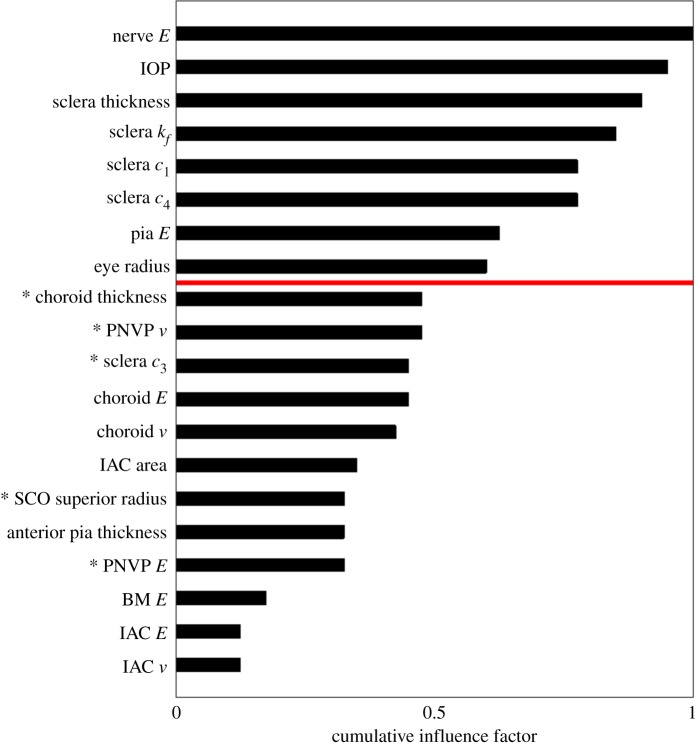
Within the baseline model, areas of high strain were observed along the inferior and superior sides of the nerve, with slightly higher strains in the inferior nerve (figure 4). The six parameters demonstrating the largest influence on optic nerve strains were, in ranked order: optic nerve stiffness, IOP, scleral thickness, sclera $k_f$, sclera $c_1$ and sclera $c_4$ (figure 5). These parameters, pia mater stiffness and eye radius were significantly correlated with both 95th percentile first principal strain and 5th percentile third principal strain. Choroidal thickness, perineural vascular plexus $\nu$, sclera $c_3$ and perineural vascular plexus stiffness were significantly correlated with 5th percentile third principal strain. Scleral canal opening superior radius was significantly correlated with 95th percentile first principal strain. The least influential parameters were scleral canal opening superior radius, anterior pia mater thickness, perineural vascular plexus stiffness, BM stiffness, inferior arterial canal stiffness and inferior arterial canal $\nu$.

Figure 5.

Tornado plot showing the cumulative influence factor for each parameter included in the sensitivity study. The cumulative influence factor represents the relative influence that each parameter had on our outcome measures: 95th percentile first principal strain and 5th percentile third principal strain. Parameters above the red line were significantly correlated, after Bonferroni's correction (see text), with both outcome measures. Parameters with (*) were significantly correlated with only one outcome measurement. IOP, intraocular pressure; BM, Bruch's membrane; PNVP, perineural vascular plexus; SCO, scleral canal opening; IAC, inferior arterial canal.

4. Discussion

We developed a parametrized model of the rat ONH and used it to investigate the influence of geometry and tissue material properties on rat optic nerve strains. Although sensitivity studies have been performed on the human ONH using parametrized models [28,29,44], the authors of those studies were able to take advantage of the near axisymmetric anatomy of the human ONH and build axisymmetric models. We overcame the difficulties introduced by the less-symmetric geometry of the rat ONH by automating a series of lofting and Boolean operations to construct our models.

We found that scleral properties were highly influential on rat optic nerve strain. Indeed, other than IOP and optic nerve stiffness, four of the six most influential parameters were features of the sclera: thickness, $k_f$, $c_1$ and $c_4$ (figure 5). Previous sensitivity studies on the human eye also found that scleral properties were some of the most influential parameters on ONH biomechanics [29,44,45]. However, it is interesting to note that the sclera parameter $c_3$ was much less influential. Since $c_1$ is the only term that affects scleral compressive stiffness and since $c_4$ is in the exponent term of the strain energy density function, it is not surprising that they are highly influential. Furthermore, previous studies have found that removing s-glycosaminoglycans from the sclera ground substance, which would likely correlate most with changes in $c_1$, had a substantial effect on scleral biomechanical behaviour [46,47]. This is consistent with our findings. However, what was surprising was that sclera $c_1$ and $c_4$ were so much more influential than sclera $c_3$. This result is likely because we accounted for preload, i.e. we evaluated strains occurring due to increases in IOP from a reference state in which IOP was 10 mm Hg. The parameter $c_4$ becomes more dominant in the strain energy density function as stress increases and collagen fibres experience greater stretch. In other words, by focusing on strains referenced to an IOP of 10 mm Hg, we did not include IOP levels in which $c_3$ might have dominated scleral tensile stiffness, and therefore likely would have had higher influence on optic nerve strains.

The high influence of the scleral $k_f$ parameter is not unexpected, but nonetheless is important to note. Highly detailed information about scleral fibre organization is starting to become available [48,49], but data for the rat are still inadequate for precise modelling. A previous study using small angle light scattering provided an important first step for quantifying regional rat scleral fibre direction and degree of alignment, but the results were highly variable from rat to rat [38]. Our previous inverse modelling study on the rat sclera also returned highly variable fibre directions and alignment values [11]. The results shown here indicate the importance of applying new technologies to quantify fibre organization in the rat sclera to inform future modelling attempts. In addition, as $c_4$ is meant to model the uncrimping rate of collagen fibres, fibre crimp data should also be gathered.

The strain patterns viewed in the baseline model were very similar to those seen in the individual-specific models of our previous study that were assigned circumferential peripapillary collagen fibres [11]. In the baseline model, strain concentrations along the inferior and superior sides of the nerve were more pronounced than along the temporal and nasal sides, and the highest strains occurred in the inferior nerve. The pattern of high inferior strain is likely due to the presence of the central retinal vessels and inferior arterial canal on the inferior side of the nerve. These vessels and canal create a ‘weak spot’ in the sclera, which results in higher inferior nerve strains. In addition, as with the individual-specific models, the optic nerve experienced more compressive strain than tensile strain. Strain magnitudes were also similar, with the range of values in this study containing those observed in the individual-specific modelling study. In addition, the baseline model strain magnitudes at 30 mm Hg for 95th percentile first principal strain and 5th percentile third principal strain were just below and within the individual-specific ranges, respectively. These similarities suggest that we effectively represented the rat ONH geometry with the parametrized model. This could be more rigorously confirmed by quantifying regional strains in the individual-specific and parametrized models; however, this would be difficult due to the way the rat optic nerve cross-sectional shape changes as it passes posteriorly through the BM, choroid and sclera.

The data from the current study indicate that strain patterns in the rat ONH can be effectively represented using the parametrized model (or possibly a slightly improved version as discussed below). This has an important implication: use of parametrized models will decrease or potentially even eliminate the need for highly labour-intensive individual-specific modelling, requiring manual delineation of tissue boundaries by 3D point clouds [10]. Instead, ‘near’-individual-specific modelling based on measurements of histology or non-invasive ONH imaging could be carried out within rat glaucoma studies with high numbers of animal subjects. More specifically, we mean that the parametrized modelling approach would be used to generate a geometry informed directly by key measurements on a given eye. The resulting model would not match the in vivo anatomy as precisely as a geometry derived from 3D point clouds; hence, the term ‘near’-individual-specific. Such an approach would allow ONH damage or cell response patterns from a rat eye to be directly compared with strain patterns from matching finite-element models. This type of study would be extremely powerful for determining how specific forms of biomechanical insult result lead to specific types of damage or cellular responses in the ONH.

The relatively high influence of the choroidal and pia mater stiffnesses make these tissues good targets for future studies aimed at determining rat ONH material properties. However, the geometry of the parametrized model from this study may need to be refined to confirm the importance of the choroidal stiffness. For simplicity, the choroid was modelled as having a constant thickness throughout the entire posterior eye, which likely resulted in overestimating its average thickness. Unlike scleral and pia mater stiffnesses, increased choroid stiffness resulted in increased optic nerve strains. Like the sclera, the pia mater is reinforced with collagen fibres [39,40], so efforts should be made to quantify their organization and stiffness in the rat. Such stiffness properties will be quite challenging to assess since the rat pia mater is very difficult to isolate.

Of the parameters at the bottom of the influence rankings, only anterior pia mater thickness was surprising. We had hypothesized that pia mater properties would be highly influential in the rat because the rat optic nerve is surrounded by pia mater tissue as far anterior as BM, whereas the pia mater in the human terminates at the posterior sclera. On the other hand, it is helpful to know that perineural vascular plexus stiffness, stiffness of tissue within the inferior arterial canal and BM stiffness are not highly influential, as they would be extremely difficult to access in order to measure their material properties. Of course, as discussed in the Limitations section, this conclusion assumes that we chose good ranges within which to vary these parameters.

5. Limitations

Perhaps the greatest limitation of this study is that, like other many finite-element efforts, the results from these models have not been validated. It may be possible to do so as non-invasive imaging, such as optical coherence tomography, improves, but even still will be extremely challenging.

As in our previous individual-specific modelling work [10,11], another major limitation of this study is our lack of knowledge about the material properties in the rat ONH. In one sense, this lack of knowledge made the current study highly worthwhile because it allowed us to identify first priorities for future tissue characterization studies. Nevertheless, this lack of knowledge may have affected the results. For example, incorrect material property baseline values or ranges can bias sensitivity study results, e.g. specifying unrealistically wide ranges for a parameter can artificially increase its cumulative influence factor. In addition, although our model was definitely an improvement from one in which the sclera was represented as a neo-Hookean material, the sclera was here represented as having only a single layer of collagen fibres, and as only having three subregions with unique fibre directions: peripheral sclera, peripapillary sclera proper and the scleral sling. In reality, the sclera likely has multiple layers of fibres, and differing fibre organization by layer and location [48,50]. Lastly, as tissues that were ranked as being highly and moderately influential, the pia mater and choroid should be modelled differently. Specifically, we recommend that the pia mater be represented with a fibre-reinforced material model; unfortunately, the best way to represent choroidal properties is unclear.

Even though the parametrized models successfully recreated the overall strain patterns observed in the individual-specific modelling study, there were also limitations with the parametrized geometries. Although parametrized models such as ours can never perfectly represent true anatomy, there are some aspects of the current model that could be improved while maintaining the ability to automatically generate ONH geometries. The most important of these is the assumption of constant thickness for the sclera. In addition, we informed the scleral thickness in this model with measurements that were taken in and near the peripapillary sclera [12]. Future work should include a sclera that, at the very least, varies in thickness with distance from the ONH and incorporates measurements of thickness from the peripheral sclera. As mentioned, the same improvements should be made to the choroid.

We chose to quantify strains within the anterior optic nerve, defined as the nerve tissue between the BM surface and the posterior scleral surface. This meant that the region within which we quantified strains varied with choroidal and scleral thicknesses, which may have artificially increased the influence of these parameters. However, a similar situation would have occurred had we picked an absolute distance from BM within which to quantify strains. Therefore, we chose to use the current analysis method since we were most interested in strain values within and anterior to the scleral canal, the region where glaucomatous damage occurs [7,51].

We also acknowledge that using linear tetrahedral elements during these simulations was a limitation due to the risk of locking in near-incompressibility. To determine if locking was a significant issue in the present work, we ran additional simulations using a nodal integration approach for tetrahedral elements, established by Gee et al. and implemented into FEBio specifically to avoid locking with linear tetrahedral elements [26,52]. Simulations conducted with this approach produced strains that were indistinguishable from those obtained using the default integration approach. Further, we did not observe any signs of element locking in either set of simulations. Thus, we do not believe that locking affected our results, including the overall ranking of the most influential parameters in the rat ONH.

Constraints should be added to the anterior faces of the CRA and CRV. In most models, the CRA (and adjacent CRV wall) ‘bends’ around the scleral sling towards the superior CRV wall. This causes high strains in the small areas of the anterior–inferior nerve (not the main strain concentration seen in the superior–inferior slice view) that are adjacent to the CRA, as can be seen in the en face view (figure 4). It was for this reason that we chose not to consider CRA stiffness, CRV stiffness or blood pressure in this study, since we were concerned that varying these properties may have resulted in numerical convergence issues. These factors could be considered in future studies after constraints are added to the anterior vessels' surfaces to prevent unrealistic deformations from happening.

6. Conclusion

We developed a parametrized finite-element model of the rat ONH and used it to carry out a sensitivity study evaluating the influence of six geometric parameters, 13 material properties and IOP on optic nerve strains. The patterns and magnitudes coincided well with those observed in our previous study using individual-specific geometries, including the pattern that the highest strains occurred in the inferior optic nerve. After optic nerve stiffness and IOP, the most influential parameters were those that specified scleral thickness, degree of scleral fibre alignment, scleral fibre stiffness and scleral ground substance stiffness. Thus, effort should be made to determine more accurate values for these properties. The results from this study can be used to inform future modelling studies, as well as studies aimed at determining rat ONH tissue material properties. In addition, an improved version of this parametrized model could potentially be used to generate near-individual-specific rat ONH finite-element models in rat glaucoma studies in order to learn more about how patterns of biomechanical insult result in damage and influence cell behaviour in glaucoma.

Data accessibility

We have included relevant data in the electronic supplementary material.

Authors' contributions

S.A.S. designed the study, made all measurements, wrote all modelling code, wrote data analysis code, performed all modelling simulations, performed all data analysis and drafted the manuscript. A.J.F. advised on Latin hypercube sampling strategy, wrote data analysis code and drafted the manuscript. C.R.E. designed the study and drafted the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the National Institutes of Health (grant nos. R01 EY025286 (C.R.E.), T32 EY007092 (S.A.S.), F31 EY028832 (S.A.S.)), Georgia Research Alliance (C.R.E.) and the Department of Veterans Affairs RR&D Service Career Development Award (grant no. RX002342; A.J.F.).