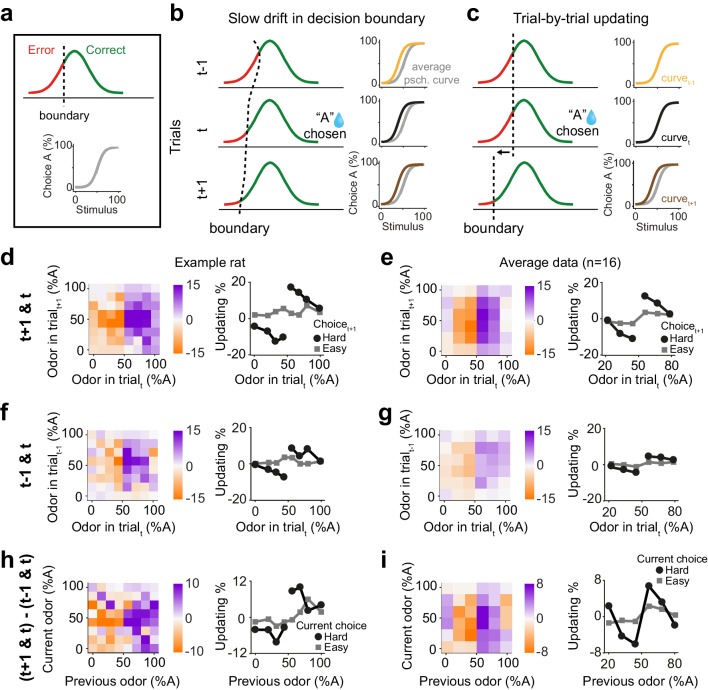
Figure 2. Choice updating is not due to slow and nonspecific drift in response bias.
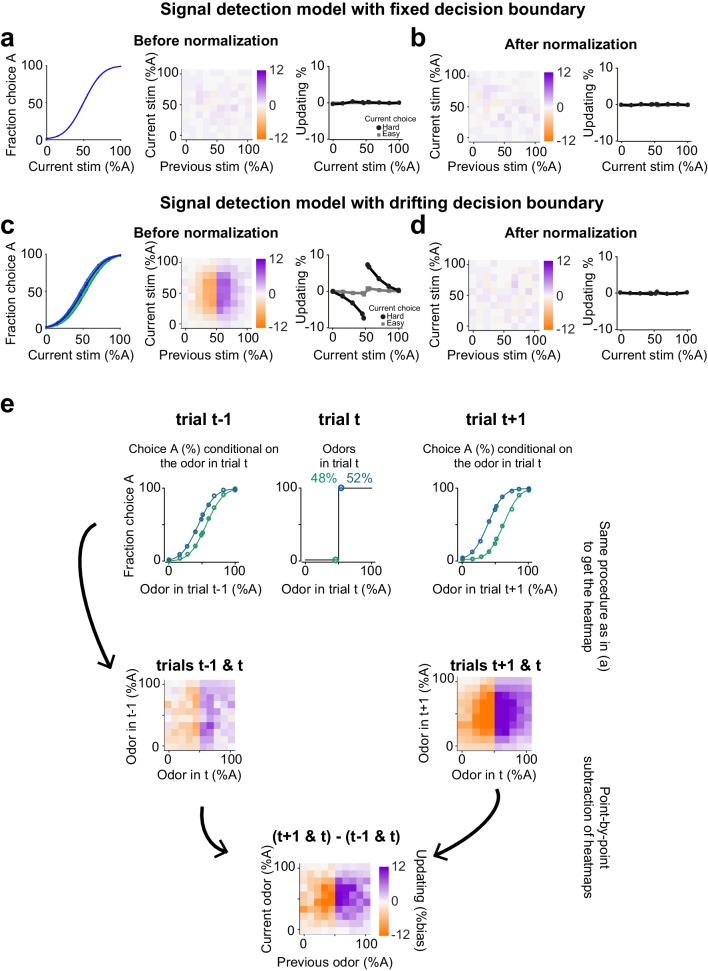
(a) Signal detection theory-inspired schematic of task performance. The psychometric curve illustrates the average choice behavior. (b) Slow non-specific drift in choice bias, visualized here as drift in the decision boundary, could lead to shift in psychometric curves which persisted for several trials and was not specific to stimulus and outcome of the previous trial. This global bias effect is cancelled when subtracting the psychometric curve of trialt-1 (orange) from trialt+1 (brown). (c) Trial-by-trial updating of decision boundary shifts psychometric curves depending on the outcome and perceptual difficulty of the preceding trial. Subtracting psychometric curves does not cancel this effect. (d) Choice bias of the example rat following a rewarded trial. (e) Similar to d but for population. (f) Choice bias of the example rat in one trial prior to current trial, reflecting global nonspecific bias visualized in b. (g) Similar to f but for population. (h) Subtracting choice bias in trialt-1 from trialt+1 reveals the trial-by-trial choice updating in the example rat. (i) Similar to h but for the population. See Figure 2—figure supplement 1 for details of the normalization procedure.