Fig. 1. The magnetic interactions and Hamiltonian of PbCuTe₂O₆.

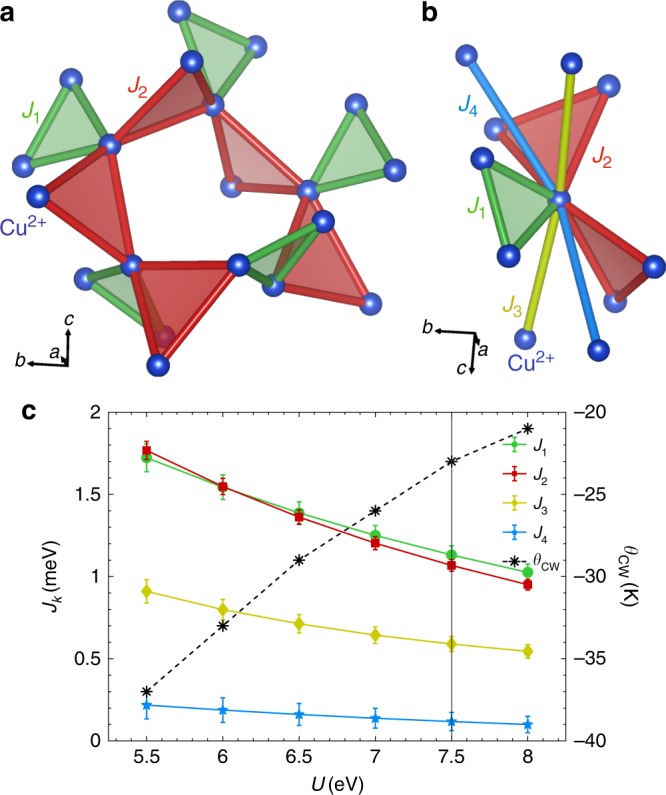
a The magnetic structure drawn from the crystallographically equivalent magnetic $S=\frac{1}{2}$ Cu²⁺ ions considering only the 1st and 2nd nearest-neighbour interactions J₁ and J₂ respectively. J₁ forms isolated equilateral triangles whereas J₂ leads to a three-dimensional network of corner-sharing triangles also known as the hyperkagome lattice. Here, the triangles on the outer Cu²⁺ ions are dropped for simplicity. The 3rd and 4th neighbour couplings J₃ and J₄, respectively, are also included in b and couple the Cu²⁺ ions into chains. The chains formed by J₃ run parallel to the cubic a–c axes while the chains due to J₄ follow the body diagonals. PbCuTe₂O₆ crystallises in cubic symmetry with space group P4₁32 and the Cu²⁺ ions occupy a single Wyckoff site²⁶. The graph in c shows the strengths of the four nearest-neighbour interactions as a function of Cu²⁺ onsite interaction U calculated by density functional theory (coloured symbols, left hand axis). These calculations were performed with the full potential local orbital (FPLO) basis set³¹, and the generalised gradient approximation functional⁴²; the coupling constants were then determined by fitting to the Hamiltonian in Eq. (1). The error bars indicate statistical errors of the fit. The Curie-Weiss temperature was calculated for each set of exchange constants using ${\theta }_{\mathrm{CW}}=-\frac{S\left(S+1\right)}{3k_b}{\sum }_{k=1}^4{z}_k{J}_k$ (for single-counting of bonds) where z_k is the coordination number of the $J_k^{\mathrm{th}}$ interaction (black stars, right hand axis). All the interactions are antiferromagnetic and they have the ratio $J_1:J_2:J_3:J_4\approx 1:1:0.5:0.1$. J₁ and J₂ are approximately equal, and much stronger than J₃ and J₄. Together, J₁ and J₂ result in the hyper-hyperkagome lattice where each magnetic ion participates in three corner-sharing triangles forming closed loops of 4 spins and 6 spins (compared to two triangles and 10-spin loops in the hyperkagome lattice).