Fig. 9.

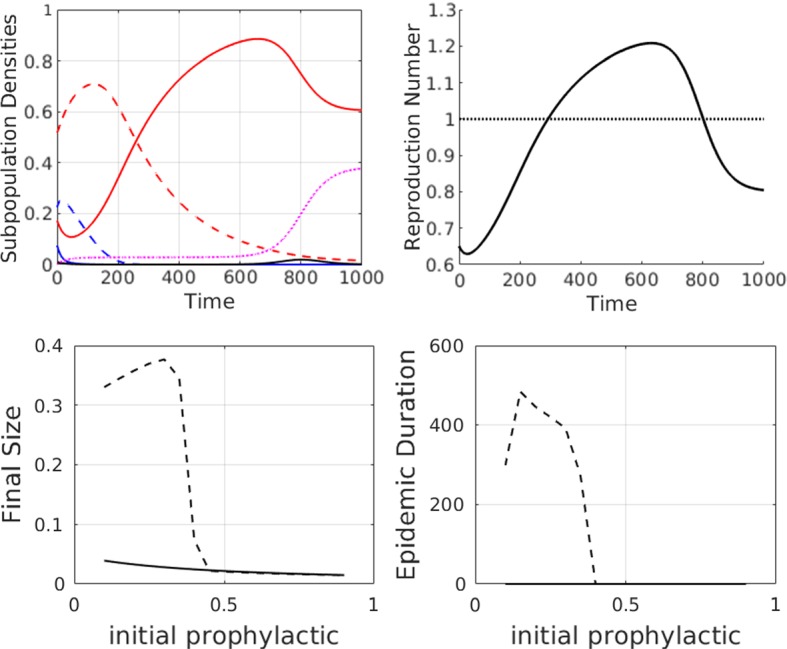
First row: simulations to show how opinion dynamics can delay the onset of an epidemic, as compared to the simple SIR case with a single susceptible population $S=S_2$. Parameter values are at the defaults as given in Table 2 except ${\beta }_0=0.131$. Colour legend for the top left subplot: red curves are $S_2$ (solid) and $S_1$ (dashed). Blue curves are $S_{-2}$ (solid) and $S_{-1}$ (dashed). Black and purple curves are I(t) and R(t), respectively. Numerical solutions are shown for the full model with fixed-order saturating influence. Susceptible attitudes are initially distributed as a “non-prophylactic majority” where $S_{-2}=S_{-1}=0.15$, $S_2=S_1=0.345$, and $I(0)=0.01$. The effective reproduction number, $\mathcal{R}(t)$, is shown in the top right subplot. The horizontal line indicates the epidemic threshold above which $\dot{I}(t)>0$. Second row: summary data plots showing how the final size, peak size, and duration of the epidemic vary as a function of the initial population proportion that is more prophylactic ($S_{-2}+S_{-1}$). Dashed line: full model with fixed- order saturating influence and solid line: SIR model with distribution of susceptibles but no interactions (${\omega }_0=0$). Note that epidemic duration is zero for all initial distribution of susceptibles if there is no interaction between susceptible groups (Color figure online)