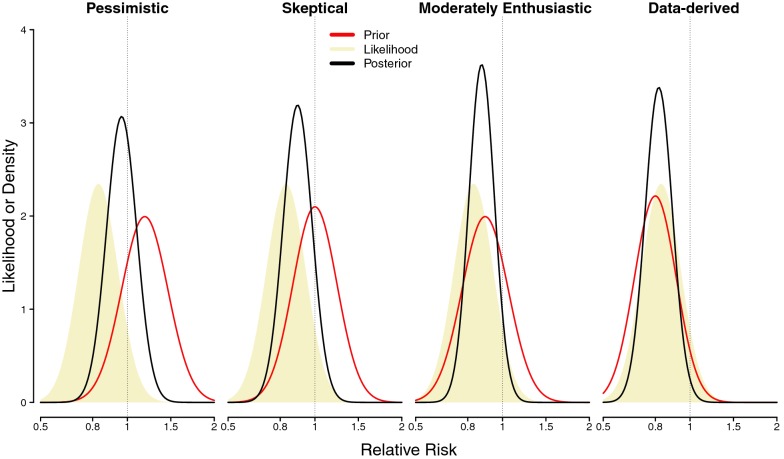
Fig. 2.

Depiction of a hypothetical Bayesian trial analysis using four different prior probability distributions. To conduct a Bayesian trial analysis, researchers must first select (ideally a priori) “priors,” (shown in red in the figure). Priors are meant to reflect the range of potential effect distributions that are expected before starting a trial. These priors are combined with the observed treatment effect in the trial (referred to as the likelihood function; indicated by the light brown shading). A Bayesian trial analysis typically uses a range of prior distributions, but the likelihood function is constant as it reflects the actual data observed in the trial. Each prior distribution is statistically combined with the likelihood function to create the Bayesian treatment effect estimate (i.e., posterior probability) distribution (outlined in black). As shown, the Bayesian treatment effect estimates may vary considerably based on the selected prior. There are several possible methods for choosing priors including (i) using results of observational studies, trials, or meta-analyses, (ii) eliciting expert opinion, or (iii) using a range of hypothetical distributions that assume very skeptical to enthusiastic effect distributions. The selection of priors is a critically important step in Bayesian trial analysis, and interested readers are directed to a recent technical tutorial [64], and the Bayesian re-analyses of the EOLIA [67] and ANDROMEDA-SHOCK trials [68] for guidance on prior selection and execution of a Bayesian analysis