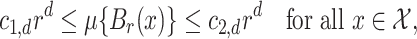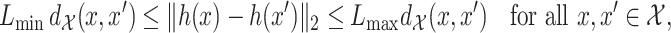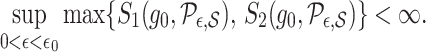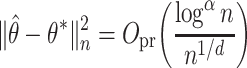Summary
The fused lasso, also known as total-variation denoising, is a locally adaptive function estimator over a regular grid of design points. In this article, we extend the fused lasso to settings in which the points do not occur on a regular grid, leading to a method for nonparametric regression. This approach, which we call the 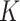 -nearest-neighbours fused lasso, involves computing the
-nearest-neighbours fused lasso, involves computing the 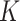 -nearest-neighbours graph of the design points and then performing the fused lasso over this graph. We show that this procedure has a number of theoretical advantages over competing methods: specifically, it inherits local adaptivity from its connection to the fused lasso, and it inherits manifold adaptivity from its connection to the
-nearest-neighbours graph of the design points and then performing the fused lasso over this graph. We show that this procedure has a number of theoretical advantages over competing methods: specifically, it inherits local adaptivity from its connection to the fused lasso, and it inherits manifold adaptivity from its connection to the 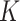 -nearest-neighbours approach. In a simulation study and an application to flu data, we show that excellent results are obtained. For completeness, we also study an estimator that makes use of an
-nearest-neighbours approach. In a simulation study and an application to flu data, we show that excellent results are obtained. For completeness, we also study an estimator that makes use of an 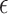 -graph rather than a
-graph rather than a 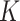 -nearest-neighbours graph and contrast it with the
-nearest-neighbours graph and contrast it with the 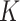 -nearest-neighbours fused lasso.
-nearest-neighbours fused lasso.
Keywords: Fused lasso, Local adaptivity, Manifold adaptivity, Nonparametric regression, Total variation
1. Introduction
This article considers the nonparametric regression setting in which we have  observations,
observations, 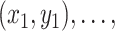
 , of the pair of random variables
, of the pair of random variables 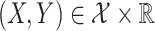 , where
, where 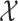 is a metric space with metric
is a metric space with metric 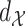 . We assume that the model
. We assume that the model
 |
(1) |
holds, where 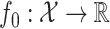 is an unknown function that we wish to estimate. This problem arises in many settings, including demographic applications (Petersen et al., 2016a; Sadhanala & Tibshirani, 2018), environmental data analysis (Hengl et al., 2007), image processing (Rudin et al., 1992) and causal inference (Wager & Athey, 2018).
is an unknown function that we wish to estimate. This problem arises in many settings, including demographic applications (Petersen et al., 2016a; Sadhanala & Tibshirani, 2018), environmental data analysis (Hengl et al., 2007), image processing (Rudin et al., 1992) and causal inference (Wager & Athey, 2018).
A substantial body of work has dealt with estimating the function  in (1) at the observations
in (1) at the observations 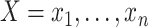 , i.e., denoising, as well as at other values of the random variable
, i.e., denoising, as well as at other values of the random variable 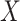 , i.e., prediction. This includes the seminal papers by Duchon (1977), Breiman et al. (1984) and Friedman (1991), as well as more recent work by Petersen et al. (2016a,b)and Sadhanala & Tibshirani (2018). A number of previous papers have focused in particular on manifold adaptivity, i.e., adapting to the dimensionality of the data; these include work on local polynomial regression by Bickel & Li (2007) and Cheng & Wu (2013),
, i.e., prediction. This includes the seminal papers by Duchon (1977), Breiman et al. (1984) and Friedman (1991), as well as more recent work by Petersen et al. (2016a,b)and Sadhanala & Tibshirani (2018). A number of previous papers have focused in particular on manifold adaptivity, i.e., adapting to the dimensionality of the data; these include work on local polynomial regression by Bickel & Li (2007) and Cheng & Wu (2013), 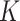 -nearest-neighbours regression by Kpotufe (2011), Gaussian processes by Yang & Tokdar (2015) and Yang & Dunson (2016), and tree-based estimators such as those in Kpotufe (2009) and Kpotufe & Dasgupta (2012). We refer the reader to Györfi et al. (2006) for a detailed survey of other classical nonparametric regression methods. The vast majority of these methods perform well in function classes with variation controlled uniformly throughout the domain, such as Lipschitz and
-nearest-neighbours regression by Kpotufe (2011), Gaussian processes by Yang & Tokdar (2015) and Yang & Dunson (2016), and tree-based estimators such as those in Kpotufe (2009) and Kpotufe & Dasgupta (2012). We refer the reader to Györfi et al. (2006) for a detailed survey of other classical nonparametric regression methods. The vast majority of these methods perform well in function classes with variation controlled uniformly throughout the domain, such as Lipschitz and  Sobolev classes. Donoho & Johnstone (1998) and Härdle et al. (2012) generalized this setting by considering functions of bounded variation and Besov classes. In this article, we focus on piecewise-Lipschitz and bounded-variation functions, as these classes can have functions with nonsmooth regions as well as smooth regions (Wang et al., 2016).
Sobolev classes. Donoho & Johnstone (1998) and Härdle et al. (2012) generalized this setting by considering functions of bounded variation and Besov classes. In this article, we focus on piecewise-Lipschitz and bounded-variation functions, as these classes can have functions with nonsmooth regions as well as smooth regions (Wang et al., 2016).
Recently, interest has focused on so-called trend filtering (Kim et al., 2009), which seeks to estimate 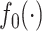 under the assumption that its discrete derivatives are sparse, in a setting in which one has access to an unweighted graph that quantifies the pairwise relationships between the
under the assumption that its discrete derivatives are sparse, in a setting in which one has access to an unweighted graph that quantifies the pairwise relationships between the 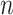 observations. In particular, the fused lasso, also known as zeroth-order trend filtering or total variation denoising (Rudin et al., 1992; Mammen & van de Geer, 1997; Tibshirani et al., 2005; Wang et al., 2016), solves the optimization problem
observations. In particular, the fused lasso, also known as zeroth-order trend filtering or total variation denoising (Rudin et al., 1992; Mammen & van de Geer, 1997; Tibshirani et al., 2005; Wang et al., 2016), solves the optimization problem
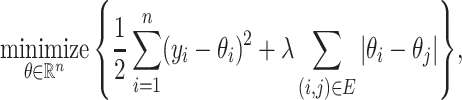 |
(2) |
where 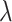 is a nonnegative tuning parameter and
is a nonnegative tuning parameter and 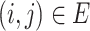 if and only if there is an edge between the
if and only if there is an edge between the 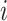 th and
th and 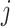 th observations in the underlying graph. Then
th observations in the underlying graph. Then  . Computational aspects of the fused lasso have been studied extensively in the case of chain graphs (Davies & Kovac, 2001; Johnson, 2013; Barbero & Sra, 2017) and for general graphs (Chambolle & Darbon, 2009; Hoefling, 2010; Chambolle & Pock, 2011; Tibshirani & Taylor, 2011; Landrieu & Obozinski, 2016). Furthermore, the fused lasso is known to have excellent theoretical properties. In one dimension, Mammen & van de Geer (1997) and Tibshirani (2014) showed that the fused lasso attains nearly minimax rates in mean squared error for estimating functions of bounded variation. More recently, also in one dimension, Guntuboyina et al. (2018) and Lin et al. (2017) independently proved that the fused lasso is nearly minimax under the assumption that
. Computational aspects of the fused lasso have been studied extensively in the case of chain graphs (Davies & Kovac, 2001; Johnson, 2013; Barbero & Sra, 2017) and for general graphs (Chambolle & Darbon, 2009; Hoefling, 2010; Chambolle & Pock, 2011; Tibshirani & Taylor, 2011; Landrieu & Obozinski, 2016). Furthermore, the fused lasso is known to have excellent theoretical properties. In one dimension, Mammen & van de Geer (1997) and Tibshirani (2014) showed that the fused lasso attains nearly minimax rates in mean squared error for estimating functions of bounded variation. More recently, also in one dimension, Guntuboyina et al. (2018) and Lin et al. (2017) independently proved that the fused lasso is nearly minimax under the assumption that  is piecewise constant. In grid graphs, Hutter & Rigollet (2016) and Sadhanala et al. (2016, 2017) proved minimax results for the fused lasso when estimating signals of interest in applications of image denoising. In more general graph structures, Padilla et al. (2018) showed that the fused lasso is consistent for denoising problems, provided that the underlying signal has total variation along the graph which when divided by
is piecewise constant. In grid graphs, Hutter & Rigollet (2016) and Sadhanala et al. (2016, 2017) proved minimax results for the fused lasso when estimating signals of interest in applications of image denoising. In more general graph structures, Padilla et al. (2018) showed that the fused lasso is consistent for denoising problems, provided that the underlying signal has total variation along the graph which when divided by  goes to zero. Other graph models that have been studied in the literature include tree graphs in Ortelli & van de Geer (2018) and Padilla et al. (2018), and star and Erdős-Rényi graphs in Hutter & Rigollet (2016).
goes to zero. Other graph models that have been studied in the literature include tree graphs in Ortelli & van de Geer (2018) and Padilla et al. (2018), and star and Erdős-Rényi graphs in Hutter & Rigollet (2016).
In this paper, we extend the utility of the fused lasso approach by combining it with the 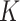 -nearest-neighbours, or
-nearest-neighbours, or 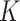 -NN, procedure. The
-NN, procedure. The 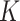 -NN has been well-studied from theoretical (Stone, 1977; Alamgir et al., 2014; Chaudhuri & Dasgupta, 2014; Von Luxburg et al., 2014), methodological (Dasgupta, 2012; Dasgupta & Kpotufe, 2014; Kontorovich et al., 2016; Singh & Póczos, 2016) and algorithmic (Friedman et al., 1977; Zhang et al., 2012; Dasgupta & Sinha, 2013) perspectives. One key feature of
-NN has been well-studied from theoretical (Stone, 1977; Alamgir et al., 2014; Chaudhuri & Dasgupta, 2014; Von Luxburg et al., 2014), methodological (Dasgupta, 2012; Dasgupta & Kpotufe, 2014; Kontorovich et al., 2016; Singh & Póczos, 2016) and algorithmic (Friedman et al., 1977; Zhang et al., 2012; Dasgupta & Sinha, 2013) perspectives. One key feature of 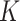 -NN methods is that they automatically have a finer resolution in regions with a higher density of design points; this is particularly consequential when the underlying density is highly nonuniform. We study the extreme case in which the data are supported over multiple manifolds of mixed intrinsic dimension. An estimator that adapts to this setting is said to achieve manifold adaptivity.
-NN methods is that they automatically have a finer resolution in regions with a higher density of design points; this is particularly consequential when the underlying density is highly nonuniform. We study the extreme case in which the data are supported over multiple manifolds of mixed intrinsic dimension. An estimator that adapts to this setting is said to achieve manifold adaptivity.
We exploit recent theoretical developments in the fused lasso and the 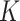 -NN procedure to derive a single approach that inherits the advantages of both methods. In greater detail, we extend the fused lasso to the general nonparametric setting of (1) by performing a two-step procedure.
-NN procedure to derive a single approach that inherits the advantages of both methods. In greater detail, we extend the fused lasso to the general nonparametric setting of (1) by performing a two-step procedure.
Step 1. We construct a 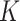 -NN graph by placing an edge between each observation and the
-NN graph by placing an edge between each observation and the  observations to which it is closest in terms of the metric
observations to which it is closest in terms of the metric 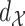 .
.
Step 2. We apply the fused lasso to this 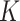 -NN graph.
-NN graph.
The resulting 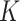 -NN fused lasso estimator appeared in the context of image processing in Elmoataz et al. (2008) and Ferradans et al. (2014), and more recently in an application of graph trend filtering in Wang et al. (2016). The present article is the first to study its theoretical properties. We also consider a variant obtained by replacing the
-NN fused lasso estimator appeared in the context of image processing in Elmoataz et al. (2008) and Ferradans et al. (2014), and more recently in an application of graph trend filtering in Wang et al. (2016). The present article is the first to study its theoretical properties. We also consider a variant obtained by replacing the  -NN graph in Step 1 with an
-NN graph in Step 1 with an 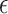 -nearest-neighbour,
-nearest-neighbour, 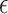 -NN, graph, which contains an edge between
-NN, graph, which contains an edge between 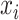 and
and 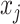 only if
only if 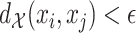 .
.
The main contributions of this paper are the following.
(i) Local adaptivity. We show that provided 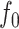 has bounded variation and satisfies an additional condition that generalizes piecewise-Lipschitz continuity, then the mean squared errors of both the
has bounded variation and satisfies an additional condition that generalizes piecewise-Lipschitz continuity, then the mean squared errors of both the 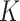 -NN fused lasso estimator and the
-NN fused lasso estimator and the 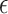 -NN fused lasso estimator scale like
-NN fused lasso estimator scale like 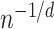 , ignoring logarithmic factors; here,
, ignoring logarithmic factors; here, 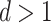 is the dimension of
is the dimension of 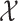 . In fact, this matches the minimax rate for estimating a two-dimensional Lipschitz function (Györfi et al., 2006), but over a much wider function class.
. In fact, this matches the minimax rate for estimating a two-dimensional Lipschitz function (Györfi et al., 2006), but over a much wider function class.
(ii) Manifold adaptivity. Suppose that the covariates are independent and identically distributed samples from a mixture model  , where
, where  are unknown bounded densities and the weights
are unknown bounded densities and the weights 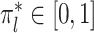 satisfy
satisfy 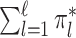 = 1. Suppose further that for
= 1. Suppose further that for 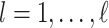 , the support
, the support 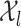 of
of 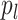 is homeomorphic to
is homeomorphic to 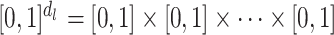 , where
, where 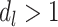 is the intrinsic dimension of
is the intrinsic dimension of 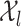 . We show that under mild conditions, if the restriction of
. We show that under mild conditions, if the restriction of  to
to 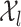 is a function of bounded variation, then the
is a function of bounded variation, then the 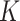 -NN fused lasso estimator attains the rate
-NN fused lasso estimator attains the rate 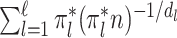 . For intuition about this rate, observe that
. For intuition about this rate, observe that 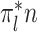 is the expected number of samples from the
is the expected number of samples from the 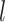 th component, and hence
th component, and hence 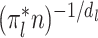 is the expected rate for the
is the expected rate for the 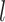 th component. Therefore, our rate is the weighted average of the expected rates for the different components.
th component. Therefore, our rate is the weighted average of the expected rates for the different components.
2. Methodology
2.1. The 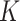 -NN and
-NN and 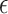 -NN fused lasso estimators
-NN fused lasso estimators
Both the 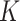 -NN and the
-NN and the 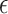 -NN fused lasso approaches are simple two-step procedures. The first step involves constructing a graph on the
-NN fused lasso approaches are simple two-step procedures. The first step involves constructing a graph on the 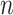 observations. The
observations. The 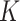 -NN graph,
-NN graph,  , has vertex set
, has vertex set 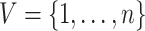 , and its edge set
, and its edge set  contains the pair
contains the pair 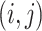 if and only if
if and only if 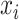 is among the
is among the 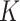 nearest neighbors of
nearest neighbors of 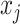 , with respect to the metric
, with respect to the metric  , and vice versa. By contrast, for the
, and vice versa. By contrast, for the 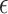 -graph
-graph 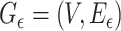 , the pair
, the pair 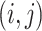 is in
is in  if and only if
if and only if 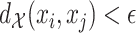 .
.
After constructing the graph, the fused lasso is applied to 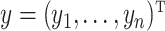 over the graph
over the graph  (either
(either  or
or  ). We can rewrite the fused lasso optimization problem (2) as
). We can rewrite the fused lasso optimization problem (2) as
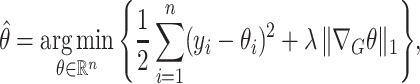 |
(3) |
where 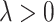 is a tuning parameter and
is a tuning parameter and  is an oriented incidence matrix of
is an oriented incidence matrix of 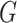 ; each row of
; each row of 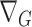 corresponds to an edge in
corresponds to an edge in 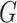 . For instance, if the
. For instance, if the  th edge in
th edge in 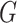 connects the
connects the 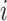 th and
th and  th observations, then
th observations, then
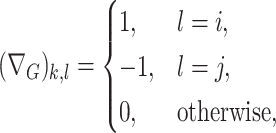 |
and so 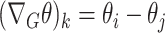 . This definition of
. This definition of  implicitly assumes an ordering of the nodes and edges, which may be chosen arbitrarily without loss of generality. In this paper we mostly focus on the setting where
implicitly assumes an ordering of the nodes and edges, which may be chosen arbitrarily without loss of generality. In this paper we mostly focus on the setting where 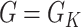 is the
is the 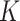 -NN graph. We also include an analysis of the
-NN graph. We also include an analysis of the 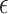 -graph, which results from taking
-graph, which results from taking 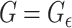 , as a point of contrast.
, as a point of contrast.
Given the estimator 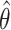 defined in (3), we predict the response at a new observation
defined in (3), we predict the response at a new observation 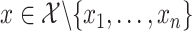 according to
according to
 |
(4) |
In the case of  -NN fused lasso, we take
-NN fused lasso, we take  , where
, where 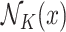 is the set of
is the set of  nearest neighbours of
nearest neighbours of  in the training data. For the
in the training data. For the  -NN fused lasso, we take
-NN fused lasso, we take 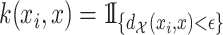 . Given a set
. Given a set  ,
, 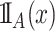 is the indicator function that equals
is the indicator function that equals 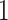 if
if 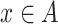 and
and  otherwise. For the
otherwise. For the  -NN fused lasso estimator, the prediction rule in (4) may not be well-defined if all the training points are farther than
-NN fused lasso estimator, the prediction rule in (4) may not be well-defined if all the training points are farther than  from
from 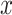 . When that is the case, we set
. When that is the case, we set  to equal the fitted value of the nearest training point.
to equal the fitted value of the nearest training point.
We construct the 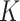 -NN and
-NN and 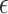 -NN graphs using standard Matlab functions such as knnsearch and bsxfun; this results in a computational complexity of
-NN graphs using standard Matlab functions such as knnsearch and bsxfun; this results in a computational complexity of 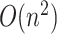 . We solve the fused lasso with the parametric max-flow algorithm of Chambolle & Darbon (2009). The procedure is in practice much faster than its worst-case complexity of
. We solve the fused lasso with the parametric max-flow algorithm of Chambolle & Darbon (2009). The procedure is in practice much faster than its worst-case complexity of 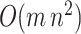 , where
, where 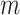 is the number of edges in the graph (Boykov & Kolmogorov, 2004; Chambolle & Darbon, 2009).
is the number of edges in the graph (Boykov & Kolmogorov, 2004; Chambolle & Darbon, 2009).
In 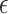 -NN and
-NN and 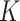 -NN, the values of
-NN, the values of  and
and 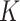 directly affect the sparsity of the graphs and hence the computational performance of the fused lasso estimators. Corollary 3.23 in Miller et al. (1997) provides an upper bound on the maximum degree of arbitrary
directly affect the sparsity of the graphs and hence the computational performance of the fused lasso estimators. Corollary 3.23 in Miller et al. (1997) provides an upper bound on the maximum degree of arbitrary  -NN graphs in
-NN graphs in  .
.
2.2. Example
To illustrate the main advantages of the 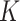 -NN fused lasso, we construct a simple example. The ability to adapt to the local smoothness of the regression function will be referred to as local adaptivity, and the ability to adapt to the density of the design points will be referred to as manifold adaptivity. The performance gains of the
-NN fused lasso, we construct a simple example. The ability to adapt to the local smoothness of the regression function will be referred to as local adaptivity, and the ability to adapt to the density of the design points will be referred to as manifold adaptivity. The performance gains of the 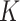 -NN fused lasso are most pronounced when these two effects happen in concert, i.e., when the regression function is less smooth where design points are denser. These properties are manifested in the following example.
-NN fused lasso are most pronounced when these two effects happen in concert, i.e., when the regression function is less smooth where design points are denser. These properties are manifested in the following example.
We generate 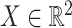 according to the probability density function
according to the probability density function
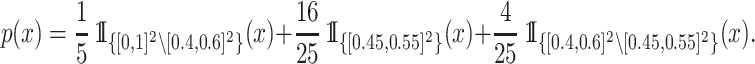 |
(5) |
Thus,  concentrates 64% of its mass in the small interval
concentrates 64% of its mass in the small interval  and 80% of its mass in
and 80% of its mass in 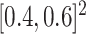 . Figure 1(a) displays a heatmap of
. Figure 1(a) displays a heatmap of 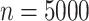 observations drawn from (5).
observations drawn from (5).
Figure 1.
(a) Heatmap of 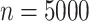 draws from (5). (b)
draws from (5). (b) 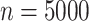 samples generated as in (1), with independent and identically distributed
samples generated as in (1), with independent and identically distributed  ,
, 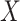 having probability density function as in (5), and
having probability density function as in (5), and  as given in (6); the vertical axis corresponds to
as given in (6); the vertical axis corresponds to 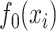 and the other two axes display the two covariates.
and the other two axes display the two covariates.
We define 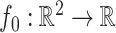 in (1) to be the piecewise-constant function
in (1) to be the piecewise-constant function
 |
(6) |
We then generate 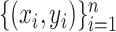 with
with 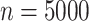 from (1); the regression function is displayed in Fig. 1(b). This simulation study has the following characteristics: the function
from (1); the regression function is displayed in Fig. 1(b). This simulation study has the following characteristics: the function 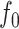 in (6) is not Lipschitz, but does have low total variation; and the probability density function
in (6) is not Lipschitz, but does have low total variation; and the probability density function 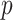 is nonuniform with higher density in the region where
is nonuniform with higher density in the region where  is less smooth.
is less smooth.
We compared the following methods in this example:
(i)
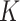 -NN fused lasso, with the number of neighbours set to
-NN fused lasso, with the number of neighbours set to 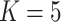 and the tuning parameter
and the tuning parameter 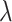 chosen to minimize the average mean squared error over 100 Monte Carlo replicates;
chosen to minimize the average mean squared error over 100 Monte Carlo replicates;(ii) classification and regression trees, CART (Breiman et al., 1984), with the complexity parameter chosen to minimize the average mean squared error over 100 Monte Carlo replicates;
(iii)
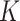 -NN regression (see, e.g., Stone, 1977), with the number of neighbours
-NN regression (see, e.g., Stone, 1977), with the number of neighbours 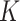 set to minimize the average mean squared error over 100 Monte Carlo replicates.
set to minimize the average mean squared error over 100 Monte Carlo replicates.
The estimated regression functions resulting from these three approaches are displayed in Fig. 2. We see that the 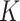 -NN fused lasso can adapt to low-density and high-density regions of the distribution of covariates, as well as to the local structure of the regression function. By contrast, the method of Breiman et al. (1984) displays some artifacts due to the binary splits that make up the decision tree, and
-NN fused lasso can adapt to low-density and high-density regions of the distribution of covariates, as well as to the local structure of the regression function. By contrast, the method of Breiman et al. (1984) displays some artifacts due to the binary splits that make up the decision tree, and 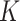 -NN regression undersmooths in large areas of the domain.
-NN regression undersmooths in large areas of the domain.
Figure 2.
(a) The function 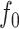 in (6), evaluated on an evenly spaced grid of size
in (6), evaluated on an evenly spaced grid of size 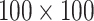 in
in 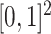 ; (b) the estimate of
; (b) the estimate of 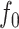 obtained via the
obtained via the 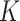 -NN fused lasso; (c) the estimate of
-NN fused lasso; (c) the estimate of 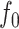 obtained via CART; (d) the estimate of
obtained via CART; (d) the estimate of 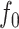 obtained via
obtained via  -NN regression.
-NN regression.
In practice, we anticipate that the 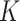 -NN fused lasso will outperform its competitors when the data are highly concentrated around a low-dimensional manifold, and the regression function is nonsmooth in that region, as in the above example. In our theoretical analysis, we will consider the special case in which the data lie precisely on a low-dimensional manifold or a mixture of low-dimensional manifolds.
-NN fused lasso will outperform its competitors when the data are highly concentrated around a low-dimensional manifold, and the regression function is nonsmooth in that region, as in the above example. In our theoretical analysis, we will consider the special case in which the data lie precisely on a low-dimensional manifold or a mixture of low-dimensional manifolds.
3. Local adaptivity of the 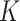 -NN and
-NN and  -NN fused lasso approaches
-NN fused lasso approaches
3.1. Assumptions
We assume that in (1) the elements of  are independent and identically distributed zero-mean sub-Gaussian random variables:
are independent and identically distributed zero-mean sub-Gaussian random variables:
 |
(7) |
for some positive constants  and
and 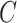 . Furthermore, we assume that
. Furthermore, we assume that  is independent of
is independent of 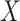 .
.
In addition, for a set  with
with  a metric space, we write
a metric space, we write 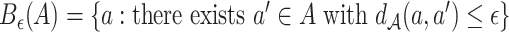 . Let
. Let 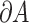 denote the boundary of the set
denote the boundary of the set 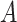 . The mean squared error of
. The mean squared error of 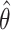 is defined as
is defined as 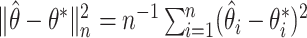 . The Euclidean norm of a vector
. The Euclidean norm of a vector  is denoted by
is denoted by 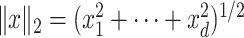 . For
. For 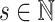 , write
, write  . In the covariate space
. In the covariate space 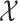 , we consider the Borel
, we consider the Borel 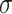 -algebra
-algebra 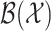 induced by the metric
induced by the metric 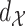 . Let
. Let  be a measure on
be a measure on 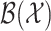 . We complement the model in (1) by assuming that the covariates independently satisfy
. We complement the model in (1) by assuming that the covariates independently satisfy 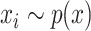 . Thus,
. Thus, 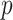 is the probability density function of the distribution of the
is the probability density function of the distribution of the 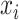 with respect to the measure space
with respect to the measure space 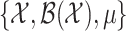 . Note that
. Note that 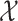 can be a manifold of dimension
can be a manifold of dimension 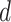 in a space of much higher dimension.
in a space of much higher dimension.
We begin by stating assumptions on the distribution of the covariates  and on the metric space
and on the metric space  . In the theoretical results in Györfi et al. (2006, §3), it is assumed that
. In the theoretical results in Györfi et al. (2006, §3), it is assumed that 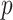 is the probability density function of the uniform distribution on
is the probability density function of the uniform distribution on  . In this section we will require only that
. In this section we will require only that 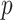 be bounded above and below. This condition appeared in the framework for studying
be bounded above and below. This condition appeared in the framework for studying 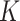 -NN graphs in Von Luxburg et al. (2014) and in the work on density quantization by Alamgir et al. (2014).
-NN graphs in Von Luxburg et al. (2014) and in the work on density quantization by Alamgir et al. (2014).
Assumption 1.
The density
satisfies
for all
, where
.
Although we do not require that 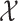 be a Euclidean space, we do require that balls in
be a Euclidean space, we do require that balls in  have volume, with respect to
have volume, with respect to 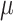 , that behaves similarly to the Lebesgue measure of balls in
, that behaves similarly to the Lebesgue measure of balls in  . This is expressed in the next assumption, which appeared as part of the definition of a valid region in Von Luxburg et al. (2014, Definition 2).
. This is expressed in the next assumption, which appeared as part of the definition of a valid region in Von Luxburg et al. (2014, Definition 2).
Assumption 2.
The base measure
in
satisfies
for all
, where
,
and
are positive constants and
is the intrinsic dimension of
.
Next, we make an assumption about the topology of the space 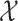 . We require that the space have no holes and be topologically equivalent to
. We require that the space have no holes and be topologically equivalent to  , in the sense that there exists a continuous bijection between
, in the sense that there exists a continuous bijection between  and
and  .
.
Assumption 3.
There exists a homeomorphism
, i.e., a continuous bijection with a continuous inverse, such that
for some positive constants
and
, where
is the intrinsic dimension of
.
Assumptions 2 and 3 immediately hold if we take 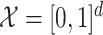 , with
, with 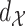 the Euclidean distance,
the Euclidean distance, 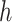 the identity mapping in
the identity mapping in  , and
, and 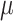 the Lebesgue measure in
the Lebesgue measure in  . A metric space
. A metric space 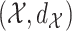 that satisfies Assumption 3 is a special case of a differential manifold; the intuition is that the space
that satisfies Assumption 3 is a special case of a differential manifold; the intuition is that the space 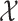 is a chart of the atlas for this differential manifold.
is a chart of the atlas for this differential manifold.
In Assumptions 2 and 3 we assume 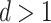 , since local adaptivity in nonparametric regression is well understood in one dimension. For example, see Tibshirani (2014), Wang et al. (2016), Guntuboyina et al. (2018) and references therein.
, since local adaptivity in nonparametric regression is well understood in one dimension. For example, see Tibshirani (2014), Wang et al. (2016), Guntuboyina et al. (2018) and references therein.
We now state conditions on the regression function 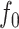 defined in (1). The first assumption simply requires bounded variation of the composition of the regression function with the homeomorphism
defined in (1). The first assumption simply requires bounded variation of the composition of the regression function with the homeomorphism  from Assumption 3.
from Assumption 3.
Assumption 4.
The function
has bounded variation, i.e.,
, and is also bounded. Here
is the interior of
, and
is the class of functions in
of bounded variation. We refer the reader to the Supplementary Material for the explicit construction of the
class. The function
was defined in Assumption 3.
If 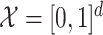 and
and 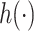 is the identity function in
is the identity function in 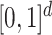 , then Assumption 4 simply says that
, then Assumption 4 simply says that  has bounded variation. However, to allow for more general scenarios, the condition is stated in terms of the function
has bounded variation. However, to allow for more general scenarios, the condition is stated in terms of the function  which has domain in the unit box, whereas the domain of
which has domain in the unit box, whereas the domain of 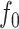 is the more general set
is the more general set 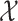 .
.
We now recall the definition of a piecewise-Lipschitz function, which induces a much larger class than the set of Lipschitz functions, as it allows for discontinuities.
Definition 1.
Let
. We say that a bounded function
is piecewise Lipschitz if there exists a set
that has the following properties.
(i) The set
has Lebesgue measure zero.
(ii) For some constants
, we have that
for all
.
(iii) There exists a positive constant
such that if
and
belong to the same connected component of
, then
.
Roughly speaking, Definition 1 says that 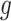 is piecewise Lipschitz if there exists a small set
is piecewise Lipschitz if there exists a small set 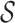 that partitions
that partitions 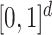 in such a way that
in such a way that 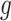 is Lipschitz within each connected component of the partition. Theorem 2.2.1 in Ziemer (2012) implies that if
is Lipschitz within each connected component of the partition. Theorem 2.2.1 in Ziemer (2012) implies that if 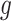 is piecewise Lipschitz, then
is piecewise Lipschitz, then 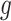 has bounded variation on any open set within a connected component.
has bounded variation on any open set within a connected component.
Theorem 1 will require Assumption 5, which is a milder condition on 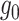 than piecewise Lipschitz continuity. We now define some notation that is needed in order to introduce Assumption 5.
than piecewise Lipschitz continuity. We now define some notation that is needed in order to introduce Assumption 5.
For 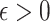 small enough, we denote by
small enough, we denote by 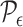 a rectangular partition of
a rectangular partition of 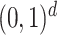 induced by
induced by 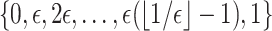 , so that all the elements of
, so that all the elements of 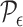 have volume of order
have volume of order 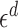 . Define
. Define 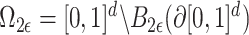 . Then, for a set
. Then, for a set  , define
, define
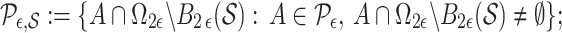 |
this is the partition induced in 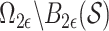 by the grid
by the grid 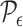 .
.
For a function  with domain
with domain  , define
, define
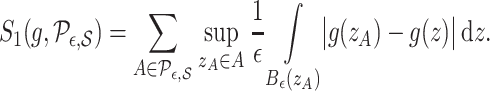 |
(8) |
If 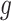 is piecewise Lipschitz, then
is piecewise Lipschitz, then  is bounded; see the Supplementary Material.
is bounded; see the Supplementary Material.
Next, define
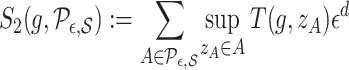 |
(9) |
with
 |
(10) |
where 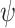 is a test function; see the Supplementary Material. Thus (9) is the summation, over evenly sized rectangles of volume
is a test function; see the Supplementary Material. Thus (9) is the summation, over evenly sized rectangles of volume 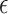 that intersect
that intersect 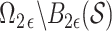 , of the supremum values of the function in (10). The latter, for a function
, of the supremum values of the function in (10). The latter, for a function 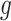 , can be thought as the average Lipschitz constant near
, can be thought as the average Lipschitz constant near 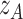 , see the expression within curly braces in (10), weighted by the derivative of a test function. The scaling factor
, see the expression within curly braces in (10), weighted by the derivative of a test function. The scaling factor 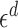 in (10) arises because the integral is taken over a set of measure proportional to
in (10) arises because the integral is taken over a set of measure proportional to 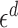 .
.
As with 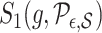 , one can verify that if
, one can verify that if 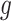 is a piecewise-Lipschitz function, then
is a piecewise-Lipschitz function, then 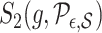 is bounded.
is bounded.
We now make use of (8) and (9) to state our next condition on 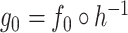 . This next condition is milder than assuming that
. This next condition is milder than assuming that 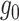 is piecewise Lipschitz; see Definition 1.
is piecewise Lipschitz; see Definition 1.
Assumption 5.
Let
. There exists a set
that has the following properties.
(i) The set
has Lebesgue measure zero.
(ii) For some constants
, we have that
for all
.
(iii) The summations
and
are bounded:
We refer the reader to the Supplementary Material for a discussion on Assumptions 4 and 5. In particular, we present an example illustrating that the class of piecewise-Lipschitz functions is, in general, different from the class of functions for which Assumptions 4 and 5 hold. However, both classes contain the class of Lipschitz functions, which is obtained by taking  in Definition 1.
in Definition 1.
3.2. Results
Letting  , we express the mean squared errors of the
, we express the mean squared errors of the 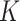 -NN fused lasso and the
-NN fused lasso and the 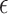 -NN fused lasso in terms of the total variation of
-NN fused lasso in terms of the total variation of 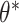 with respect to the
with respect to the 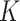 -NN and
-NN and  -NN graphs.
-NN graphs.
Theorem 1.
Let
for some
. Then under Assumptions 1–3, with an appropriate choice of the tuning parameter
, the
-NN fused lasso estimator
satisfies
This upper bound also holds for the
-NN fused lasso estimator with
if we replace
by
and make an appropriate choice of
.
Clearly, the upper bound in Theorem 1 is a function of  or
or  for the
for the 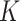 -NN or
-NN or 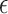 -NN graph, respectively. For the grid graph considered in Sadhanala et al. (2016),
-NN graph, respectively. For the grid graph considered in Sadhanala et al. (2016),  , leading to the rate
, leading to the rate 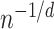 . However, for a general graph, there is no a priori reason to expect that
. However, for a general graph, there is no a priori reason to expect that 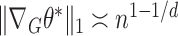 . Our next result shows that
. Our next result shows that 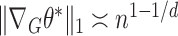 for
for 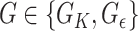 , under the assumptions discussed in § 3.1.
, under the assumptions discussed in § 3.1.
Theorem 2.
Under Assumptions 1–5 or under Assumptions 1–3 and piecewise Lipschitz continuity of
, if
for some
, then for an appropriate choice of the tuning parameter
, the
-NN fused lasso estimator defined in (3) satisfies
(11) with
. Moreover, under Assumptions 1–3 and piecewise Lipschitz continuity of
,
defined in (4) with the
-NN fused lasso estimator satisfies
(12) Furthermore, under the same assumptions, (11) and (12) hold for the
-NN fused lasso estimator with
.
Theorem 2 indicates that under Assumptions 1–5 or under Assumptions 1–3 and piecewise Lipschitz continuity of  , both the
, both the  -NN fused lasso and the
-NN fused lasso and the 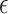 -NN fused lasso estimators attain a convergence rate of
-NN fused lasso estimators attain a convergence rate of  , ignoring logarithmic terms. Importantly, Theorem 3.2 of Györfi et al. (2006) shows that in the two-dimensional setting, this rate is actually minimax for estimation of Lipschitz-continuous functions when the design points are uniformly drawn from
, ignoring logarithmic terms. Importantly, Theorem 3.2 of Györfi et al. (2006) shows that in the two-dimensional setting, this rate is actually minimax for estimation of Lipschitz-continuous functions when the design points are uniformly drawn from 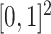 . Thus, when
. Thus, when 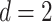 , both the
, both the 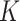 -NN fused lasso and the
-NN fused lasso and the 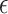 -NN fused lasso are minimax for estimating functions in the class implied by Assumptions 1–5, and also in the class of piecewise-Lipschitz functions implied by Assumptions 1–3 and Definition 1. In higher dimensions (
-NN fused lasso are minimax for estimating functions in the class implied by Assumptions 1–5, and also in the class of piecewise-Lipschitz functions implied by Assumptions 1–3 and Definition 1. In higher dimensions ( ), by the lower bound in Castro et al. (2005, Proposition 2), we can conclude that both estimators attain nearly minimax rates for estimating piecewise-Lipschitz functions, whereas it is unknown whether the same is true under Assumptions 1–5. A different method, similar in spirit to the method of Breiman et al. (1984), was introduced in Castro et al. (2005, Appendix E). Castro et al. (2005) showed that this approach is also nearly minimax for estimating elements in the class of piecewise-Lipschitz functions, although is unclear whether a computationally feasible implementation of their algorithm is available.
), by the lower bound in Castro et al. (2005, Proposition 2), we can conclude that both estimators attain nearly minimax rates for estimating piecewise-Lipschitz functions, whereas it is unknown whether the same is true under Assumptions 1–5. A different method, similar in spirit to the method of Breiman et al. (1984), was introduced in Castro et al. (2005, Appendix E). Castro et al. (2005) showed that this approach is also nearly minimax for estimating elements in the class of piecewise-Lipschitz functions, although is unclear whether a computationally feasible implementation of their algorithm is available.
We see from Theorem 2 that both of the fused lasso estimators are locally adaptive, in the sense that they can adapt to the form of the function 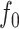 . Specifically, these estimators do not require knowledge of the set
. Specifically, these estimators do not require knowledge of the set 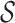 in Assumption 5 or Definition 1. This is similar in spirit to the one-dimensional fused lasso, which does not require knowledge of the breakpoints when estimating a piecewise-Lipschitz function.
in Assumption 5 or Definition 1. This is similar in spirit to the one-dimensional fused lasso, which does not require knowledge of the breakpoints when estimating a piecewise-Lipschitz function.
There is, however, an important difference in the applicability of Theorem 2 to the 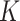 -NN fused lasso and to the
-NN fused lasso and to the 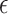 -NN fused lasso. To attain the rate in Theorem 2, the
-NN fused lasso. To attain the rate in Theorem 2, the 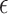 -NN fused lasso requires knowledge of the dimension
-NN fused lasso requires knowledge of the dimension 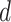 , since this quantity appears in the rate of decay of
, since this quantity appears in the rate of decay of 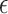 ; but in practice the value of
; but in practice the value of 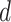 may not be clear. For instance, suppose that
may not be clear. For instance, suppose that 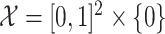 ; this is a subset of
; this is a subset of  , but it is homeomorphic to
, but it is homeomorphic to 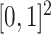 , so
, so 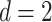 . If
. If 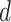 is unknown, then it can be challenging to choose
is unknown, then it can be challenging to choose 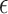 for the
for the 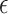 -NN fused lasso. By contrast, the choice of
-NN fused lasso. By contrast, the choice of 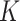 in the
in the 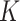 -NN fused lasso involves only the sample size
-NN fused lasso involves only the sample size 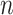 . Consequently, local adaptivity of the
. Consequently, local adaptivity of the  -NN fused lasso may be much easier to achieve in practice.
-NN fused lasso may be much easier to achieve in practice.
4. Manifold adaptivity of the 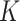 -NN fused lasso
-NN fused lasso
In this section, we allow the observations 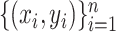 to be drawn from a mixture distribution in which each mixture component satisfies the assumptions in § 3. Under these assumptions, we show that the
to be drawn from a mixture distribution in which each mixture component satisfies the assumptions in § 3. Under these assumptions, we show that the 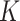 -NN fused lasso estimator can still achieve a desirable rate.
-NN fused lasso estimator can still achieve a desirable rate.
We assume
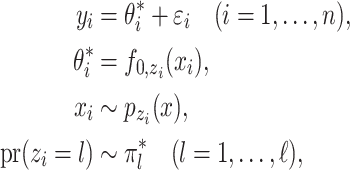 |
(13) |
where 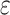 satisfies (7),
satisfies (7), 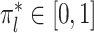 with
with 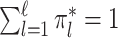 ,
,  is a density with support
is a density with support 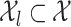 ,
, 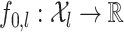 , and
, and 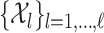 is a collection of subsets of
is a collection of subsets of  . For simplicity, we will assume that
. For simplicity, we will assume that 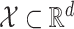 for some
for some 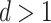 and that
and that  is the Euclidean distance. In (13), the observed data are
is the Euclidean distance. In (13), the observed data are 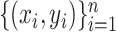 . The remaining ingredients in (13) are either latent or unknown.
. The remaining ingredients in (13) are either latent or unknown.
We further assume that each set 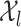 is homeomorphic to a Euclidean box of dimension depending on
is homeomorphic to a Euclidean box of dimension depending on  , as follows.
, as follows.
Assumption 6.
For
, the set
satisfies Assumptions 1–3 with metric given by
, dimension
, and
equal to some measure
. In addition, the following hold.
such that the set
satisfies
for any small enough
(14) .
such that for any
, either
or
(15) for all
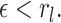
The constraints implied by Assumption 6 are very natural. Inequality (14) states that the intersections of the manifolds  are small. To put this into perspective, if the extrinsic space (
are small. To put this into perspective, if the extrinsic space ( ) were
) were  with Lebesgue measure, then balls of radius of
with Lebesgue measure, then balls of radius of 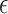 would have measure
would have measure 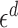 , which is less than
, which is less than 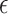 for all
for all  , and the set
, and the set  would have measure that scales like
would have measure that scales like 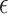 , which is the same scaling as in (14). Furthermore, (15) holds if
, which is the same scaling as in (14). Furthermore, (15) holds if  are compact and convex subsets of
are compact and convex subsets of  whose interiors are disjoint.
whose interiors are disjoint.
We are now ready to extend Theorem 2 to the framework described in this section.
Theorem 3.
Suppose the data are generated as in (13) and that Assumption 6 holds. Suppose also that the functions
either satisfy Assumptions 4 and 5 or are piecewise Lipschitz in the domain
. Then for an appropriate choice of the tuning parameter
, the
-NN fused lasso estimator defined in (3) satisfies
provided that
and
for some constants
, where
is a polynomial function. Here, the
are allowed to change with
.
When  for all
for all 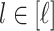 in Theorem 3, we obtain, ignoring logarithmic factors, the rate
in Theorem 3, we obtain, ignoring logarithmic factors, the rate 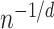 , which is minimax when the functions
, which is minimax when the functions 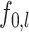 are piecewise Lipschitz. The rate is also minimax when
are piecewise Lipschitz. The rate is also minimax when  and the functions
and the functions 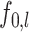 satisfy Assumptions 4 and 5. In addition, our rates can be compared with those in the existing literature on manifold adaptivity. Specifically, when
satisfy Assumptions 4 and 5. In addition, our rates can be compared with those in the existing literature on manifold adaptivity. Specifically, when 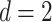 , the rate
, the rate 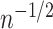 is attained by local polynomial regression (Bickel & Li, 2007) and Gaussian process regression (Yang & Dunson, 2016) for the class of differentiable functions with bounded partial derivatives, and by
is attained by local polynomial regression (Bickel & Li, 2007) and Gaussian process regression (Yang & Dunson, 2016) for the class of differentiable functions with bounded partial derivatives, and by 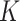 -NN regression for Lipschitz functions (Kpotufe, 2011). In higher dimensions, the methods of Bickel & Li (2007), Yang & Dunson (2016) and Kpotufe (2011) attain better rates than
-NN regression for Lipschitz functions (Kpotufe, 2011). In higher dimensions, the methods of Bickel & Li (2007), Yang & Dunson (2016) and Kpotufe (2011) attain better rates than 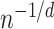 on smaller classes of functions that do not allow for discontinuities.
on smaller classes of functions that do not allow for discontinuities.
Finally, we refer the reader to the Supplementary Material for an example suggesting that the 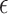 -NN fused lasso estimator may not be manifold adaptive.
-NN fused lasso estimator may not be manifold adaptive.
5. Experiments
5.1. Simulated data
Throughout this section, we take 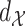 to be Euclidean distance. We compare the following approaches:
to be Euclidean distance. We compare the following approaches:
(i) the
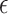 -NN fused lasso, with
-NN fused lasso, with 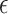 held fixed and
held fixed and 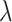 treated as a tuning parameter;
treated as a tuning parameter;(ii) the
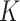 -NN fused lasso, with
-NN fused lasso, with 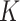 held fixed and
held fixed and 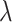 treated as a tuning parameter;
treated as a tuning parameter;(iii) CART (Breiman et al., 1984), implemented in the R (R Development Core Team, 2020) package rpart, with the complexity parameter treated as a tuning parameter;
(iv) multivariate adaptive regression splines, mars (Friedman, 1991), implemented in the R package earth, with the penalty parameter treated as a tuning parameter;
(v) random forests, RF (Breiman, 2001), implemented in the R package randomForest, with the number of trees fixed at 800 and with the minimum size of each terminal node treated as a tuning parameter;
(vi)
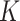 -NN regression (e.g., Stone, 1977), implemented in Matlab using the function knnsearch, with
-NN regression (e.g., Stone, 1977), implemented in Matlab using the function knnsearch, with 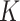 treated as a tuning parameter.
treated as a tuning parameter.
We evaluate each method’s performance in terms of the mean squared error, as defined in § 3.1. Specifically, we apply each method to 150 Monte Carlo datasets with a range of tuning parameter values. For each method, we then identify the tuning parameter value that leads to the smallest average mean squared error over the 150 datasets. We refer to this smallest average mean squared error as the optimized mean squared error in what follows.
In our first two scenarios we consider 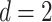 covariates and let the sample size
covariates and let the sample size  vary.
vary.
Scenario 1. The function 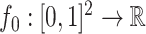 is piecewise constant,
is piecewise constant,
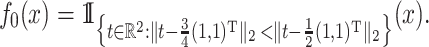 |
The covariates are drawn from a uniform distribution on 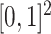 . The data are generated as in (1) with
. The data are generated as in (1) with 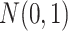 errors.
errors.
Scenario 2. The function  is as in (6), with generative density for
is as in (6), with generative density for 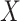 as in (5). The data are generated as in (1) with
as in (5). The data are generated as in (1) with  errors.
errors.
Data generated under Scenario 1 are displayed in Fig. 3(a). Data generated under Scenario 2 are displayed in Fig. 1(b).
Figure 3.
(a) Scatterplot of data generated under Scenario 1; the vertical axis displays 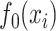 and the other two axes display the two covariates. (b) Optimized mean squared error, MSE, averaged over 150 Monte Carlo simulations, of competing methods under Scenario 1; here
and the other two axes display the two covariates. (b) Optimized mean squared error, MSE, averaged over 150 Monte Carlo simulations, of competing methods under Scenario 1; here  and
and 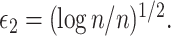 (c) Computational time, in seconds for Scenario 1, averaged over 150 Monte Carlo simulations. (d) Optimized mean squared error, averaged over 150 Monte Carlo simulations, of competing methods under Scenario 2. The methods under comparison are MARS (green solid line and asterisks), CART (red dashed line and plus signs),
(c) Computational time, in seconds for Scenario 1, averaged over 150 Monte Carlo simulations. (d) Optimized mean squared error, averaged over 150 Monte Carlo simulations, of competing methods under Scenario 2. The methods under comparison are MARS (green solid line and asterisks), CART (red dashed line and plus signs),  -NN (olive dashed line and crosses), 3-NN fused lasso (blue dashed line and downward-pointing triangles), 4-NN fused lasso (blue dashed line and upward-pointing triangles), 5-NN fused lasso (blue dashed line and rightward-pointing triangles),
-NN (olive dashed line and crosses), 3-NN fused lasso (blue dashed line and downward-pointing triangles), 4-NN fused lasso (blue dashed line and upward-pointing triangles), 5-NN fused lasso (blue dashed line and rightward-pointing triangles),  -NN fused lasso (purple dashed line and squares),
-NN fused lasso (purple dashed line and squares), 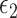 -NN fused lasso (purple dashed line and stars), and RF (gold dashed line and diamonds).
-NN fused lasso (purple dashed line and stars), and RF (gold dashed line and diamonds).
Figure 3(b) and (d) display the optimized mean squared error as a function of the sample size for Scenarios 1 and 2, respectively. The 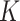 -NN fused lasso gives the best results in both scenarios. The
-NN fused lasso gives the best results in both scenarios. The 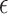 -NN fused lasso performs a little worse than
-NN fused lasso performs a little worse than 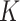 -NN fused lasso in Scenario 1, and very poorly in Scenario 2; the results are not shown.
-NN fused lasso in Scenario 1, and very poorly in Scenario 2; the results are not shown.
Timing results for all approaches under Scenario 1 are given in Fig. 3(c). For all methods, the times reported are averaged over a range of tuning parameter values. For instance, for the 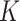 -NN fused lasso, we fix
-NN fused lasso, we fix 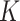 and compute the time for different choices of
and compute the time for different choices of  ; we then report the average of those times.
; we then report the average of those times.
For the next two scenarios, we consider 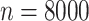 and values of
and values of 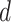 in
in 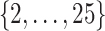 .
.
Scenario 3. The function 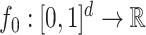 is defined as
is defined as
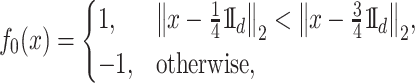 |
and the density  is uniform in
is uniform in 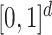 . The data are generated as in (1) with independent
. The data are generated as in (1) with independent 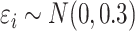 .
.
Scenario 4. The function 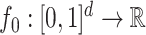 is defined as
is defined as
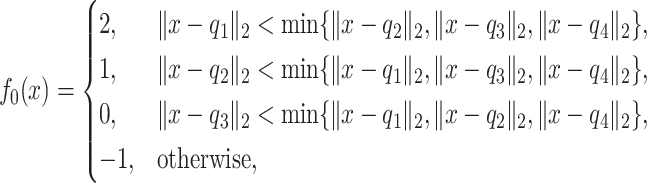 |
where 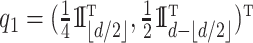 ,
, 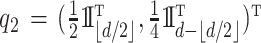 ,
,  and
and 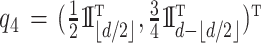 . Once again, the generative density for
. Once again, the generative density for 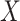 is uniform in
is uniform in 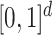 . The data are generated as in (1) with independent
. The data are generated as in (1) with independent 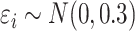 .
.
The optimized mean squared error for each approach is displayed in Fig. 4. When 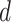 is small, most methods perform well; however, as
is small, most methods perform well; however, as 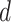 increases, the performance of the competing methods quickly deteriorates, whereas the
increases, the performance of the competing methods quickly deteriorates, whereas the 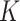 -NN fused lasso continues to perform well.
-NN fused lasso continues to perform well.
Figure 4.
Optimized mean squared error (MSE), averaged over 150 Monte Carlo simulations, for (a) Scenario 3 and (b) Scenario 4. In both scenarios, 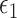 is chosen to be the largest value such that the total number of edges in the graph
is chosen to be the largest value such that the total number of edges in the graph  is at most 50 000. The methods under comparison are MARS (green solid line and asterisks), CART (red dashed line and plus signs),
is at most 50 000. The methods under comparison are MARS (green solid line and asterisks), CART (red dashed line and plus signs), 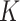 -NN (olive dashed line and crosses), 3-NN fused lasso (blue dashed line and downward-pointing triangles), 4-NN fused lasso (blue dashed line and upward-pointing triangles), 5-NN fused lasso (blue dashed line and rightward-pointing triangles),
-NN (olive dashed line and crosses), 3-NN fused lasso (blue dashed line and downward-pointing triangles), 4-NN fused lasso (blue dashed line and upward-pointing triangles), 5-NN fused lasso (blue dashed line and rightward-pointing triangles),  -NN fused lasso (purple dashed line and squares), and RF (gold dashed line and diamonds).
-NN fused lasso (purple dashed line and squares), and RF (gold dashed line and diamonds).
5.2. Flu data
The data consist of flu activity and atmospheric conditions between 1 January 2003 and 31 December 2009 in different cities across the U.S. state of Texas. Our data-use agreement does not permit dissemination of the flu activity data, which come from medical records. The atmospheric conditions, which include temperature and air quality, can be obtained directly from http://wonder.cdc.gov/. Using the number of flu-related doctor’s office visits as the dependent variable, we fit a separate nonparametric regression model to each of 24 cities; each day is treated as a separate observation, so that the number of samples is 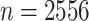 in each city. Five independent variables are included in the regression: maximum and average observed concentrations of particulate matter, maximum and minimum temperatures, and day of the year. All variables are scaled to lie in
in each city. Five independent variables are included in the regression: maximum and average observed concentrations of particulate matter, maximum and minimum temperatures, and day of the year. All variables are scaled to lie in 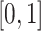 . We performed 50 75%/25% splits of the data into a training set and a test set. All models were fitted on the training data, using five-fold cross-validation to select tuning parameter values. Then prediction performance was evaluated on the test set.
. We performed 50 75%/25% splits of the data into a training set and a test set. All models were fitted on the training data, using five-fold cross-validation to select tuning parameter values. Then prediction performance was evaluated on the test set.
We apply the 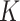 -NN fused lasso with
-NN fused lasso with 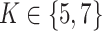 and the
and the 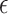 -NN fused lasso with
-NN fused lasso with 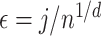 for
for 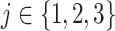 , which is motivated by Theorem 2, and with larger choices of
, which is motivated by Theorem 2, and with larger choices of 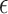 , leading to worse performance. We also fit neural networks (Hagan et al., 1996; implemented in Matlab using the functions newfit and train), thin plate splines (tps, Duchon, 1977; implemented using the R package fields), and MARS, CART and RF as described in § 5.1.
, leading to worse performance. We also fit neural networks (Hagan et al., 1996; implemented in Matlab using the functions newfit and train), thin plate splines (tps, Duchon, 1977; implemented using the R package fields), and MARS, CART and RF as described in § 5.1.
The average test set prediction error across the 50 test sets is displayed in Fig. 5. It can be seen that the 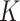 -NN fused lasso and the
-NN fused lasso and the 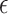 -NN fused lasso have the best performances. In particular, the
-NN fused lasso have the best performances. In particular, the 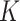 -NN fused lasso performs best in 13 out the 24 cities, and second best in 6 cities. In 8 of the 24 cities, the
-NN fused lasso performs best in 13 out the 24 cities, and second best in 6 cities. In 8 of the 24 cities, the 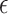 -NN fused lasso performs best.
-NN fused lasso performs best.
Figure 5.
Results for the flu data; the normalized prediction error was obtained by dividing each method’s test set prediction error by the test set prediction error of the 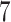 -NN fused lasso. The methods under comparison are the 5-NN fused lasso (dark blue), neural networks (olive green),
-NN fused lasso. The methods under comparison are the 5-NN fused lasso (dark blue), neural networks (olive green), 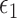 -NN fused lasso (purple),
-NN fused lasso (purple), 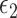 -NN fused lasso (light pink),
-NN fused lasso (light pink),  -NN fused lasso (dark pink), CART (red), MARS (green), TPS (dark grey), RF (gold) and 7-NN fused lasso (light blue).
-NN fused lasso (dark pink), CART (red), MARS (green), TPS (dark grey), RF (gold) and 7-NN fused lasso (light blue).
We contend that the 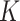 -NN fused lasso achieves superior performance because it adapts to heterogeneity in the density of design points
-NN fused lasso achieves superior performance because it adapts to heterogeneity in the density of design points  , i.e., manifold adaptivity, and adapts to heterogeneity in the smoothness of the regression function
, i.e., manifold adaptivity, and adapts to heterogeneity in the smoothness of the regression function  , i.e., local adaptivity. In our theoretical results, we have substantiated this contention through prediction error rate bounds for a large class of regression functions of heterogeneous smoothness and a large class of underlying measures with heterogeneous intrinsic dimensionality. Our experiments demonstrate that these theoretical advantages translate into practical performance gains.
, i.e., local adaptivity. In our theoretical results, we have substantiated this contention through prediction error rate bounds for a large class of regression functions of heterogeneous smoothness and a large class of underlying measures with heterogeneous intrinsic dimensionality. Our experiments demonstrate that these theoretical advantages translate into practical performance gains.
Supplementary Material
Acknowledgement
Sharpnack was partially supported by the U.S. National Science Foundation. Witten was partially supported by the U.S. National Institutes of Health, a National Science Foundation CAREER Award, and a Simons Investigator Award in Mathematical Modeling of Living Systems.
References
- Alamgir, M., Lugosi, G. & Luxburg, U. (2014). Density-preserving quantization with application to graph downsampling. Proc. Mach. Learn. Res. 35, 543–59. Proceedings of the 27th Annual Conference on Learning Theory. [Google Scholar]
- Barbero, Á. & Sra, S. (2017). Modular proximal optimization for multidimensional total-variation regularization. arXiv: 1411.0589v3. [Google Scholar]
- Bickel, P. J. & Li, B. (2007). Local polynomial regression on unknown manifolds In Complex Datasets and Inverse Problems. Beachwood, Ohio: Institute of Mathematical Statistics, pp. 177–86. [Google Scholar]
- Boykov, Y. & Kolmogorov, V. (2004). An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision. IEEE Trans. Pat. Anal. Mach. Intel. 26, 1124–37. [DOI] [PubMed] [Google Scholar]
- Breiman, L. (2001). Random forests. Mach. Learn. 45, 5–32. [Google Scholar]
- Breiman, L., Friedman, J., Stone, C. J. & Olshen, R. A. (1984). Classification and Regression Trees. Boca Raton, Florida: CRC Press. [Google Scholar]
- Castro, R. M., Willett, R. & Nowak, R. (2005). Faster rates in regression via active learning. In Proc. 18th Int. Conf. Neural Information Processing Systems. pp. 179–86. [Google Scholar]
- Chambolle, A. & Darbon, J. (2009). On total variation minimization and surface evolution using parametric maximum flows. Int. J. Comp. Vis. 84, 288–307. [Google Scholar]
- Chambolle, A. & Pock, T. (2011). A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imag. Vis. 40, 120–45. [Google Scholar]
- Chaudhuri, K. & Dasgupta, S. (2014). Rates of convergence for nearest neighbor classification. In Proc. 27th Int. Conf. Neural Information Processing Systems (NIPS’14), vol. 2 Cambridge, Massachusetts: MIT Press, pp. 3437–45. [Google Scholar]
- Cheng, M.-Y. & Wu, H.-T. (2013). Local linear regression on manifolds and its geometric interpretation. J. Am. Statist. Assoc. 108, 1421–34. [Google Scholar]
- Dasgupta, S. (2012). Consistency of nearest neighbor classification under selective sampling. Proc. Mach. Learn. Res. 23, 18.1–15. Proceedings of the 25th Annual Conference on Learning Theory. [Google Scholar]
- Dasgupta, S. & Kpotufe, S. (2014). Optimal rates for k-NN density and mode estimation. In Advances in Neural Information Processing Systems 27 (NIPS’14). San Diego, California: Neural Information Processing Systems Foundation, pp. 2555–63. [Google Scholar]
- Dasgupta, S. & Sinha, K. (2013). Randomized partition trees for exact nearest neighbor search. JMLR Workshop Conf. Proc. 30, 317–37. [Google Scholar]
- Davies, P. L. & Kovac, A. (2001). Local extremes, runs, strings and multiresolution. Ann. Statist. 29, 1–65. [Google Scholar]
- Donoho, D. L. & Johnstone, I. M. (1998). Minimax estimation via wavelet shrinkage. Ann. Statist. 26, 879–921. [Google Scholar]
- Duchon, J. (1977). Splines minimizing rotation-invariant semi-norms in Sobolev spaces. In Constructive Theory of Functions of Several Variables. Berlin: Springer, pp. 85–100. [Google Scholar]
- Elmoataz, A., Lezoray, O. & Bougleux, S. (2008). Nonlocal discrete regularization on weighted graphs: A framework for image and manifold processing. IEEE Trans. Image Proces. 17, 1047–60. [DOI] [PubMed] [Google Scholar]
- Ferradans, S., Papadakis, N., Peyré, G. & Aujol, J.-F. (2014). Regularized discrete optimal transport. SIAM J. Imag. Sci. 7, 1853–82. [Google Scholar]
- Friedman, J. H. (1991). Multivariate adaptive regression splines. Ann. Statist. 19, 1–67. [Google Scholar]
- Friedman, J. H., Bentley, J. L. & Finkel, R. A. (1977). An algorithm for finding best matches in logarithmic expected time. ACM Trans. Math. Software 3, 209–26. [Google Scholar]
- Guntuboyina, A., Lieu, D., Chatterjee, S. & Sen, B. (2018). Adaptive risk bounds in univariate total variation and trend filtering. arXiv: 1702.05113v2. [Google Scholar]
- Györfi, L., Kohler, M., Krzyzak, A. & Walk, H. (2006). A Distribution-Free Theory of Nonparametric Regression. New York: Springer. [Google Scholar]
- Hagan, M. T., Demuth, H. B., Beale, M. H. & De Jesús, O. (1996). Neural Network Design. Boston: PWS Publishing Co. [Google Scholar]
- Härdle, W., Kerkyacharian, G., Picard, D. & Tsybakov, A. (2012). Wavelets, Approximation, and Statistical Applications, vol. 129 of Lecture Notes in Statistics. New York: Springer. [Google Scholar]
- Hengl, T., Heuvelink, G. B. & Rossiter, D. G. (2007). About regression-kriging: From equations to case studies. Comp. Geosci. 33, 1301–15. [Google Scholar]
- Hoefling, H. (2010). A path algorithm for the fused lasso signal approximator. J. Comp. Graph. Statist. 19, 984–1006. [Google Scholar]
- Hutter, J.-C. & Rigollet, P. (2016). Optimal rates for total variation denoising. Proc. Mach. Learn. Res. 29, 1115–46. 29th Annual Conference on Learning Theory. [Google Scholar]
- Johnson, N. (2013). A dynamic programming algorithm for the fused lasso and l0-segmentation. J. Comp. Graph. Statist. 22, 246–60. [Google Scholar]
-
Kim, S.-J., Koh, K., Boyd, S. & Gorinevsky, D. (2009).
 trend filtering. SIAM Rev. 51, 339–60. [Google Scholar]
trend filtering. SIAM Rev. 51, 339–60. [Google Scholar] - Kontorovich, A., Sabato, S. & Urner, R. (2016). Active nearest-neighbor learning in metric spaces. In Proc. 30th Int. Conf. Neural Information Processing Systems (NIPS’16). New York: Curran Associates, pp. 856–64. [Google Scholar]
- Kpotufe, S. (2009). Escaping the curse of dimensionality with a tree-based regressor. arXiv: 0902.3453. [Google Scholar]
-
Kpotufe, S. (2011).
 -NN regression adapts to local intrinsic dimension. In Proc. 24th Int. Conf. Neural Information Processing Systems (NIPS’11). New York: Curran Associates, pp. 729–37. [Google Scholar]
-NN regression adapts to local intrinsic dimension. In Proc. 24th Int. Conf. Neural Information Processing Systems (NIPS’11). New York: Curran Associates, pp. 729–37. [Google Scholar] - Kpotufe, S. & Dasgupta, S. (2012). A tree-based regressor that adapts to intrinsic dimension. J. Comp. Syst. Sci. 78, 1496–515. [Google Scholar]
- Landrieu, L. & Obozinski, G. (2016). Cut pursuit: Fast algorithms to learn piecewise constant functions on general weighted graphs. In Proc. 19th International Conference on Artificial Intelligence and Statistics, vol. 51, 1384–93. Cadiz, Spain: PMLR. [Google Scholar]
- Lin, K., Sharpnack, J. L., Rinaldo, A. & Tibshirani, R. J. (2017). A sharp error analysis for the fused lasso, with application to approximate changepoint screening. In Proc. 31st Int. Conf. Neural Information Processing Systems (NIPS’17). New York: Curran Associates, pp. 6887–96. [Google Scholar]
- Mammen, E. & van de Geer, S. (1997). Locally adaptive regression splines. Ann. Statist. 25, 387–413. [Google Scholar]
- Miller, G. L., Teng, S.-H., Thurston, W. & Vavasis, S. A. (1997). Separators for sphere-packings and nearest neighbor graphs. J. Assoc. Comp. Mach 44, 1–29. [Google Scholar]
- Ortelli, F. & van de Geer, S. (2018). On the total variation regularized estimator over a class of tree graphs. Electron. J. Statist. 12, 4517–70. [Google Scholar]
- Padilla, O. H. M., Scott, J. G., Sharpnack, J. & Tibshirani, R. J. (2018). The DFS fused lasso: Linear-time denoising over general graphs. J. Comp. Graph. Statist. 18, 1–36. [Google Scholar]
- Petersen, A., Simon, N. & Witten, D. (2016a). Convex regression with interpretable sharp partitions. J. Comp. Graph. Statist. 17, 3240–70. [PMC free article] [PubMed] [Google Scholar]
- Petersen, A., Witten, D. & Simon, N. (2016b). Fused lasso additive model. J. Comp. Graph. Statist. 25, 1005–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria: ISBN 3-900051-07-0. http://www.R-project.org. [Google Scholar]
- Rudin, L., Osher, S. & Faterni, E. (1992). Nonlinear total variation based noise removal algorithms. Physica D 60, 259–68. [Google Scholar]
- Sadhanala, V. & Tibshirani, R. J. (2018). Additive models with trend filtering. arXiv: 1702.05037v4. [Google Scholar]
- Sadhanala, V., Wang, Y.-X., Sharpnack, J. L. & Tibshirani, R. J. (2017). Higher-order total variation classes on grids: Minimax theory and trend filtering methods. In Proc. 31st Int. Conf. Neural Information Processing Systems (NIPS’17). New York: Curran Associates, pp. 5796–806. [Google Scholar]
- Sadhanala, V., Wang, Y.-X. & Tibshirani, R. J. (2016). Total variation classes beyond 1d: Minimax rates, and the limitations of linear smoothers. In Proc. 30th Int. Conf. Neural Information Processing Systems (NIPS’16). New York: Curran Associates, pp. 3513–21. [Google Scholar]
- Singh, S. & Póczos, B. (2016). Analysis of k-nearest neighbor distances with application to entropy estimation. arXiv: 1603.08578v2. [Google Scholar]
- Stone, C. J. (1977). Consistent nonparametric regression. Ann. Statist. 5, 595–620. [Google Scholar]
- Tibshirani, R., Saunders, M., Rosset, S., Zhu, J. & Knight, K. (2005). Sparsity and smoothness via the fused lasso. J. R. Statist. Soc. B67, 91–108. [Google Scholar]
- Tibshirani, R. J. (2014). Adaptive piecewise polynomial estimation via trend filtering. Ann. Statist. 42, 285–323. [Google Scholar]
- Tibshirani, R. J. & Taylor, J. (2011). The solution path of the generalized lasso. Ann. Statist. 39, 1335–71. [Google Scholar]
- Von Luxburg, U., Radl, A. & Hein, M. (2014). Hitting and commute times in large graphs are often misleading. J. Mach. Learn. Res. 15, 1751–98. [Google Scholar]
- Wager, S. & Athey, S. (2018). Estimation and inference of heterogeneous treatment effects using random forests. J. Am. Statist. Assoc. 113, 1228–42. [Google Scholar]
- Wang, Y.-X., Sharpnack, J., Smola, A. & Tibshirani, R. J. (2016). Trend filtering on graphs. J. Mach. Learn. Res. 17, 1–41. [Google Scholar]
- Yang, Y. & Dunson, D. B. (2016). Bayesian manifold regression. Ann. Statist. 44, 876–905. [Google Scholar]
- Yang, Y. & Tokdar, S. T. (2015). Minimax-optimal nonparametric regression in high dimensions. Ann. Statist. 43, 652–74. [Google Scholar]
- Zhang, C., Li, F. & Jestes, J. (2012). Efficient parallel kNN joins for large data in MapReduce. In Proc. 15th Int. Conf. Extending Database Technology. New York: Assocation of Computing Machinery, pp. 38–49. [Google Scholar]
- Ziemer, W. P. (2012). Weakly Differentiable Functions: Sobolev Spaces and Functions of Bounded Variation. New York: Springer. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.