Abstract
Large macromolecules, including proteins and their complexes, very often adopt multiple conformations. Some of them can be seen experimentally, for example with x-ray crystallography or cryo-electron microscopy. This structural heterogeneity is not occasional and is frequently linked with specific biological function. Thus, the accurate description of macromolecular conformational transitions is crucial for understanding fundamental mechanisms of life’s machinery. We report on a real-time method to predict such transitions by extrapolating from instantaneous eigen motions, computed using the normal mode analysis, to a series of twists. We demonstrate the applicability of our approach to the prediction of a wide range of motions, including large collective opening-closing transitions and conformational changes induced by partner binding. We also highlight particularly difficult cases of very small transitions between crystal and solution structures. Our method guarantees preservation of the protein structure during the transition and allows accessing conformations that are unreachable with classical normal mode analysis. We provide practical solutions to describe localized motions with a few low-frequency modes and to relax some geometrical constraints along the predicted transitions. This work opens the way to the systematic description of protein motions, whatever their degree of collectivity. Our method is freely available as a part of the NOn-Linear rigid Block (NOLB) package.
Significance
Proteins perform their biological functions by changing their shapes and interacting with each other. Getting access to their motions is challenging. In this work, we present a method generating plausible physics-based protein motions and conformations. We model a protein as a network of atoms connected by springs and deform it along the least-energy directions. Our main contribution is to perform the deformations in a nonlinear way through a series of twists. This allows us to produce a wide range of motions, some of them previously inaccessible, and to preserve the structure of the protein during the motion. We are able to simulate the opening or closing of a protein and the changes it undergoes to adapt to a partner.
Introduction
Large macromolecules, including proteins and their complexes, are intrinsically flexible, and this flexibility is often linked with their function. A molecule in solution can be viewed as a structurally heterogeneous ensemble, in which a finite number of conformational states (e.g., active-inactive, bound-unbound) may become stable under certain conditions to perform specific tasks. Identifying the molecular states relevant to protein functioning is necessary for our understanding of biological processes. Moreover, targeting protein functional motions bears a great potential to control and modulate proteins’ activities and interactions in physiopathological contexts.
Structural heterogeneity can be probed by various experimental techniques. These include x-ray crystallography, cryo-electron microscopy (cryo-EM), NMR, small-angle scattering, and many others (1). The two first methods allow obtaining large macromolecular structures at high resolution. Whereas x-ray crystallography captures single stable states, cryo-EM allows for observing conformational ensembles in solution. The resolution attained by cryo-EM is very often lower than that of x-ray structures, mainly because of the structural heterogeneity of the measured samples. However, the ongoing revolution in cryo-EM instrumentation (2) has supplied an exponentially growing body of near-atomic resolution structures. These techniques provide valuable insights on proteins’ functioning and interactions with their environment. Nevertheless, experimental protein structure determination remains a time consuming and costly process. The systematic description of the variety of shapes a protein adopts under particular environmental conditions, upon post-translational modifications, and/or partner binding still remains out of reach. Hence, there is a need for computational tools able to efficiently and accurately predict functionally relevant protein conformations and macromolecular motions in general.
Several decades ago, Hayward and Gõ (3) observed that large-scale protein dynamics can be described with a set of just a few collective coordinates, accessible through the normal mode analysis (NMA). Thus, the latter provides an efficient way for reducing the dimensionality of the initial system and allows to study conformational transitions in proteins and their complexes. This has motivated the development of NMA-based tools for multiple biological applications, including flexible fitting of atomistic structures into cryo-EM maps (4, 5, 6, 7, 8, 9, 10, 11) or one-dimensional scattering profiles (12), prediction of crystallographic temperature factors (13,14), generation of structural ensembles for cross-docking (15,16), prediction of protein hinge regions (17,18), flexible docking (19, 20, 21, 22), refinement of crystallographic structures (23,24) and docking solutions (25, 26, 27), and many others. The suitability of the NMA to model conformational dynamics varies widely depending on the system studied and on the type of motions involved (28). The NMA was shown to better describe highly collective motions compared to localized deformations (29).
Atomistic molecular dynamics (MD) simulations represent an alternative to the NMA. They provide a practical tool to describe the structural heterogeneity around an equilibrium state and the flexibility exhibited by solvent-exposed small regions, such as loops. For instance, MD-based sampling has been applied to model the conformational diversity embedded in localized regions of cryo-EM maps (30). In addition, the concept of collective coordinates has been extended to MD (31, 32, 33), which as a result, have been applied to the study of free energy changes between different conformational states, and rare-event dynamics (34). Nevertheless, MD simulations are much more costly than the NMA, and the characterization of conformational transitions on a large scale with the former still remains computationally prohibitive.
In this work, we present an efficient real-time method to predict biomolecular transitions involving a wide range of motions, from local deformations (e.g., of a small loop) to highly collective domain motions. It relies on the nonlinear rigid block (NOLB) NMA (35). NOLB extends the classical NMA to describe nonlinear motions. Specifically, it extrapolates motions computed from instantaneous linear and angular velocities to large amplitudes. The resulting molecular motion is represented as a series of rigid block twists. We apply this nonlinear extrapolation to a combination of a few low-frequency normal modes to approximate conformational transitions. Importantly, our approach is conceptually simple and explores the conformational space in the Cartesian coordinate system. The nonlinearity of the computed motions allows a better approximation of experimentally observed transitions.
So far, the computation of nonlinear transitions using the NMA formalism has only been possible by cutting them in small steps and recomputing the normal modes at each step and/or by performing the NMA in the internal coordinate system (11,36, 37, 38). On average, the internal coordinate NMA requires a smaller number of modes than the classical Cartesian coordinate NMA to describe large structural transitions (36) and better predicts transitions upon protein docking (38). Working with internal coordinates also allows for large dimensionality reduction through variable selection and model simplification (36,39, 40, 41, 42, 43). Despite these advantages, internal coordinate NMA implies solving the generalized eigenvalue problem and dealing with necessarily dense interaction matrices. This makes it computationally costly and prevents its application on a large scale. Moreover, small changes in the internal coordinates may result in very large overall structural changes, which makes the approach less amenable to conformational space exploration because it generates instability in the solution.
To demonstrate the advantages of the method reported here, we assess structural transitions computed with the classical linear normal modes, the Cartesian nonlinear normal modes, and an iterative scheme in which the nonlinear modes are updated while progressing to the target state. For this purpose, we composed three test benchmarks of proteins exhibiting various types of structural transitions. The first test case presents examples of large domain motions, in which “open” and “closed” conformations can be clearly identified (11). The second one is comprised of proteins changing their conformation upon binding to other proteins (44). The third one contains test cases from the Cryo-EM 2015/2016 Model Challenge, in which the transition takes place between a crystal form and a conformation in solution (45). We find that the classical linear NMA behaves well on the first set, in which the motions are mostly collective, but is not suited to describe the more localized deformations and very small transitions exhibited by the two other sets. We show that our Cartesian nonlinear approach systematically obtains better transitions compared to the linear one. Indeed, the final predicted structures are closer to the experimentally known targets and display less distortions. The improvement is particularly significant on changes associated to partner binding. Also, the transitions are stereochemically correct as highlighted by high Procheck (46) G-factors along the transitions. Moreover, structures along the transitions approach several experimentally validated intermediate states. We further demonstrate the usefulness of nonlinearity and mode updating to extend the applicability of the NMA to localized and disruptive motions. We also show that if the target structure is unknown and the amplitudes of the deformations along each mode are sampled randomly, there is still a sufficiently high success rate to predict the transition. Last but not least, our approach is very computationally and memory efficient. It is implemented as a fully automated tool available at https://team.inria.fr/nano-d/software/nolb-normal-modes/.
Our results allow for revisiting the NMA-based description of biomolecular transitions. They pave the way to the systematic targeting and modulation of protein-protein interactions.
Materials and Methods
Outline of the method
Protein shapes and motions are governed by a multitude of interatomic forces, resulting from intra- and intermolecular interactions. Despite this high complexity, many functional motions can be approximated by a few low-frequency modes characteristic of the protein’s geometrical shape (29,47,48). To compute these modes, we represent the protein as an elastic network (Fig. 1, top panel on the left), in which each node stands for an atom, and two nodes i and j are connected by a spring whenever the distance dij between the corresponding atoms is smaller than a cutoff value, typically 5 Å. The normal modes are obtained by diagonalizing the mass-weighted Hessian matrix of the potential energy of this network. To reduce the dimensionality of this diagonalization problem, we consider each protein residue as a rigid block, according to the rotation translation blocks (RTB) approach (49,50) (Fig. 1, middle panel on the left). With this coarse-grained representation, the computed normal modes are composed of instantaneous linear velocities and instantaneous angular velocities , defining translations and rotations for each block/residue.
Figure 1.
Principle of the method. Left: the three main ingredients of the method are depicted: the elastic network model, the rotation translation blocks (RTB) projection, and the nonlinear extrapolation of motions. The protein is represented as an elastic network (on top), in which all the atom pairs within a certain cutoff distance are connected with harmonic springs. Coarse graining is achieved by replacing each protein residue by a rigid block (in the middle). The color code indicates the one-to-one correspondence between residues (on the left) and blocks (on the right). Each block has six degrees of freedom, three for rotation and three for translation. At each step of the transition, each residue/block undergoes a screw (twist) motion (at the bottom) defined from the instantaneous linear and angular velocities and obtained by the NMA. The initial and final atomic positions are denoted as A and , respectively. O is the origin of the coordinate system, and is the residue’s center of mass. Right: shown are examples of nonlinear transitions computed for coagulation factor VIIa upon binding to tissue factor. The intermediate structures in orange were determined from the normal modes of the known unbound structure (PDB:1qfk:HL, in gray). Those in red were further obtained by updating the normal modes three times. The final predicted structure (in opaque) is 1.3 Å from the known bound structure (PDB: 1fak:HL). To see this figure in color, go online.
A straightforward way to compute normal mode guided structural transitions is to calculate instantaneous displacements of each atom in a residue and then linearly extrapolate these up to a given amplitude a. However, at large amplitudes, this will distort interatomic distances and produce unrealistic molecular conformations. To circumvent this problem, we apply a nonlinear extrapolation (Fig. 1, bottom panel on the left), in which each residue undergoes a screw (or a twist) motion. Specifically, the linear velocity is decomposed in two terms, namely , which is collinear to , and , which is orthogonal to . We further represent the pair of and as a pure rotation around a new center . Hence, instead of rotating about the axis defined by passing through its center of mass, each residue is rotated about the new axis defined by passing through and translated only in the direction of . This nonlinear extrapolation guarantees the preservation of the stereochemical properties of the protein structure subject to the motion.
Our method computes normal mode-guided nonlinear conformational transitions, starting from an experimentally determined structure or a high-quality three-dimensional model. Specifically, normal modes are computed from the starting structure, which is then deformed along a selection of these modes up to a given amount of conformational deviation (Fig. 1, right panel). The simulated conformational change can be potentially very large (several tens of Å). The algorithm may be run in an iterative mode, in which the normal modes are recomputed on intermediate conformations. This allows modifying the topology of the network representing the structure and going further away from the starting structure (Fig. 1, right panel, compare orange and red conformations). The method guarantees producing plausible physics-based motions and conformations.
Data sets
The first test set is comprised of structures from the iMod benchmark (43) prepared by Chacón and colleagues. It was recently used to assess three coarse-grained elastic network model-based flexible fitting methods (51). It contains 23 proteins, each given in “open” and “closed” conformations, and represents a wide variety of macromolecular motions, mostly hinge motions, but also shear and other complex motions. The structures were extracted from the molecular motions database MolMovDB (52). All of them have less than 3% Ramachandran outliers (as computed by the MolProbity program (53)) and do not have any broken chain or missing atom. The average root mean-square deviation (RMSD) for this set is 5.1 ± 3.0 Å.
For the second test set, we have chosen some examples from the Protein-Protein Docking Benchmark v5 (44). This benchmark contains 230 protein complexes with at least one of the partners solved in both bound (complexed) and unbound (free) states. All structures have a resolution better than 3.25 Å, and some of them contain more than one chain. We extracted 95 proteins with Cα RMSD between the two states above 2 Å. This test set is well suited for assessing the range of the applicability of flexible docking methods (54). We should also mention that some of the structure pairs can be classified as open-closed pairs. The average displacement for this test set is 4.0 ± 3.9 Å.
For the third test set, we have selected seven cases from the Cryo-EM 2015/2016 Model Challenge (45). The initial set was comprised of eight cases, but we decided not to consider one of them, namely the 70S ribosome. The selected cases are listed in Table S1. Each one of them comprises one or several starting structures solved by x-ray crystallography and one or several target structures corresponding to a Model Challenge map. In one case (γ-secretase), we did not find homologous x-ray structures for the starting state and used several cryo-EM structures instead. The map resolutions range from 2.2 to 4.3 Å. The average Cα RMSD displacement between the two states is 2.6 ± 3.2 Å.
NMA theory
Let us consider a molecular system with N atoms at an equilibrium position . Let be the potential energy of the molecular system. Let us also introduce , a small time-dependent displacement of the system around q0. The potential energy V in the vicinity of q0 can thus be given by its quadratic approximation, which allows for analytically solving the Newton’s equation of motion:
| (1) |
where M is the diagonal mass matrix, and H is the Hessian matrix of the potential energy V evaluated at the equilibrium position q0. We then compute the square matrix of eigenvectors L and the diagonal matrix of eigenvalues Λ of the mass-weighted Hessian Hw = M−1/2HM−1/2,
| (2) |
Let us now introduce , a projection of q into the eigenspace of Hw, and (λi)i=0..3N, the diagonal values in Λ. Then, left multiplying Eq. 1 by LTM1/2 gives the following system of uncoupled equations:
| (3) |
which can be solved analytically. We will refer to the columns of the M−1/2L matrix as Cartesian linear normal modes. We should specifically mention that these normal modes are not generally orthogonal, unless all the masses in M are equal to each other.
The RTB projection method
Many methods have been proposed to reduce the dimensionality of the NMA diagonalization problem. For example, Noguti and Gõ (39) and Levitt et al. (40) and later, Ma et al. (42), Mendez and Bastolla (36), and Chacón et al. (43) explored the NMA approach in internal coordinates. However, an orthogonal idea of reducing the dimensionality of the original system by coarse graining its representation has gained much more popularity. One of the first coarse-graining methods was the RTB approach introduced by Durand et al. (49) and further developed by Tama et al. (50) and Li and Cui (55). In this method, individual or several consecutive residues are considered as rigid blocks that can only exhibit rotational and translational motions (49,50). The transition from the RTB coordinate system, consisting of n rigid blocks with 6n degrees of freedom (DOFs) to the all-atom coordinate system with 3N DOFs is performed by an orthogonal projection matrix , whose detailed form can be found elsewhere (35). We will only mention that this projection matrix is obtained by writing down the conservation laws of the linear and the angular momentum for a rigid block in mass-weighted coordinates (49).
The normal modes are then computed by the diagonalization of the RTB-projected mass-weighted Hessian,
| (4) |
where is the matrix composed of the RTB normal modes with the corresponding diagonal eigenvalue matrix . The all-atom normal modes Lw (in mass-weighted coordinates) are then obtained as a projection of the RTB normal modes , according to
| (5) |
The NOLB method
Molecular vibrations in a multidimensional harmonic oscillator are all uncoupled and can be found by solving Eq. 3. Diagonalization of the RTB-projected mass-weighted Hessian gives a set of eigenvectors that are composed of instantaneous linear velocities and instantaneous angular velocities of individual rigid blocks. For a rigid block with mass Mb and inertia tensor I, we first compute these in non-mass-weighted coordinates as follows:
| (6) |
Then, given a deformation amplitude a, the translational increment in the rigid block’s position and the angular increment in its orientation can be computed as
| (7) |
where the rigid block’s rotation is described with a unit axis passing through its center of mass and an angle ϕ. Finally, we rewrite the increment in the rigid block’s position as a sum of two orthogonal vectors,
| (8) |
where is orthogonal to , and is collinear to . We then represent the -related motion as a pure rotation about a new center , given as
| (9) |
such that the final rigid block’s positions is expressed through the initial positions as
| (10) |
where is the rotation matrix describing rigid block’s rotation about an axis by an angle . More details can be found in the original NOLB publication (35). It is easy to demonstrate that this is the only type of rigid-body motion that conserves the original kinetic energy. Indeed, using the parallel axis theorem, it is readily seen that the initial energy contribution of linear velocity is transformed into equivalent contribution from the angular velocity. As it has been noted by Juan Cortés from the Laboratory for Analysis and Architecture of Systems (LAAS-CNRS) in a private communication, the presented theory can also be formulated in terms of screw algebra, in which a screw is a six-dimensional vector constructed from a pair of three-dimensional vectors and linear and angular velocities.
Linear structural transitions
Let us assume we know two conformations of the same molecular system and the correspondence between their atoms. The latter can be robustly deduced from sequence alignment if the two systems are composed of not fully identical proteins. Let us also assume we are given the displacement vector between the two conformations after their optimal rigid superposition. It is easy to demonstrate that in this case, the center of masses of the two conformations match. We can now find the minimal RMSD between the two conformations, if one of them is allowed to deform along its M lowest normal modes , which are not necessarily orthonormal, as
| (11) |
where N is the number of atoms in the system, I is the identity matrix, and a are the optimal amplitudes of linear deformations given as
| (12) |
If the normal modes L are orthonormal (which happens if the mass matrix in Eq. 3 is identity), the above equation simplifies to
| (13) |
It can be readily seen that if all the 3N modes are activated, the matrix L becomes square, LLT turns into an identity, and the RMSD reduces to zero.
Nonlinear structural transitions
The NOLB method produces nonlinear deformations. Therefore, Eq. 11 would not be exact in this case. However, given the displacement vector between the two conformations as in the previous case, we can still construct a deterministic deformation trajectory and compute the corresponding RMSD. We should specifically mention that rotation operators do not commute, and thus, the result of applying two rotations will generally depend on the order of these operators. Therefore, to make the method deterministic, when combining several modes, we always order them from the lowest to the highest frequencies. This choice is dictated by the fact that slower modes result in larger amplitudes of thermal fluctuations.
To produce a nonlinear deformation toward the target structure, we use an iterative procedure (see Algorithm 1 in Supporting Materials and Methods). At each step of the iteration, we approximate the amplitudes of the nonlinear deformation by the analytically computed linear amplitudes using Eq. 12. This approximation will not be valid at large deformation amplitudes a. Therefore, if the RMSD computed for the linear approximation (Eq. 11) is larger than a certain threshold (we have chosen 0.1 Å), we split the deformation into smaller pieces. Each piece is computed based on the values of the linear amplitudes scaled in such a way that the total linear RMSD of the deformation equals to the threshold value of 0.1 Å. We terminate the algorithm when the maximal number of iterations is exceeded (100 by default) or if the relative deformation becomes smaller than a tolerance of 1e − 6. This algorithm can be iterated multiple times, the elastic network model being updated and the normal modes recomputed at each iteration (see Algorithm 2 in Supporting Materials and Methods). On-the-fly normal mode recomputation has been previously proposed in the context of cryo-EM fitting and morphing applications (11,37,43).
Our nonlinear model and the way we assess the predicted transitions naturally overcome the limitations of classical NMA schemes highlighted in Jernigan et al. (56,57) when the transition involves a substantial protein domain rotation.
Nonlinear random sampling
If one of the two conformations is not known, which is the case in many practical applications, the NOLB method samples the conformational space around the known structure up to a given RMSD. In this case, the amplitudes of the selected modes are chosen randomly (22). To test whether such random exploration could be useful to recapitulate functional states, we implemented a simulation protocol producing 10,000 conformations (see Algorithm 3 in Supporting Materials and Methods). In this protocol, the starting structure is first deformed along its three slowest modes; then, the modes are recomputed, and the new starting structures are deformed along their 10 slowest modes. An intermediate step with five modes is added in case of large deformations (>4.5 Å). The biggest part of the displacement is accomplished in the first step. Keeping the number of modes very small (3) at this step allows for limiting the combinatorics of the conformational search.
Potential function
Classical NMA methods can use any potential function, provided that it corresponds to the equilibrium position of the molecular system. Some recent developments can also assume nonequilibrium state of the initial system (10). In our method, we use an all-atom anisotropic network model (58,59), in which the initial structure is always at equilibrium. The all-atom anisotropic network model has the following potential function,
| (14) |
where dij is the distance between the ith and the jth atoms, is the reference distance between these atoms, as found in the original structure, γ is the spring constant, and Rc is a cutoff distance, typically between 3.5 and 15 Å. By default, we let this value to 5 Å. However, if there are loosely connected structural fragments in the system, it makes sense to increase this value to 10 Å or even more. The Hessian matrix corresponding to this potential function is composed of the following blocks (58, 59, 60):
| (15) |
where xij = xi − xj, yij = yi − yj, and zij = zi − zj. To rapidly compute this matrix, we use an efficient neighbor search algorithm (61).
Assessment of the transitions
Transition coverage
To assess the ability of NOLB to reach the target structure by deforming the starting structure along its lowest normal modes, we compute the transition coverage, expressed as
| (16) |
where RMSDi is the initial RMSD between the starting and target structures, and RMSDf is the deviation between the final structure obtained from the computed transition and the target structure. The coverage varies between 0 (null prediction) and 1 (perfect prediction).
To assess the ability of NOLB to recapitulate known intermediate structures, we computed the improvement score described in (62) and expressed as
| (17) |
where S, I, and T are the starting, intermediate, and target structures, respectively, and Pj is the jth conformation predicted by NOLB. In the best-case scenario, one of the conformations predicted by NOLB is identical to the known intermediate structure, leading to an improvement of 100%. In the worst-case scenario, all conformations predicted by NOLB are further away from the intermediate than the starting and target structures, leading to a negative value.
Collectivity
Collective motions can be characterized by their collectivity κ, which is proportional to the exponential of the information entropy (63). The collectivity of a transition between two structures of a molecule with N atoms can be computed (29) as
| (18) |
where qi are scaled Cartesian displacements of individual atoms, , with the normalization factor α taken such that . Nκ gives an effective number of nonzero displacements . Thus, κ is confined to the interval {1/N;1}. If κ = 1, then the corresponding transition is maximally collective and has all the displacements identical, which happens for rigid-body motions, for example. In the limit of an extremely localized motion, in which only one single atom is affected, κ is minimal and equals to 1/N. In a similar way, one can estimate the degree of collectivity of a normal mode. For example, collectivity of the jth mode is given by the same equation above, provided that qi are now the scaled normal mode’s displacements,
| (19) |
RESULTS AND DISCUSSION
NOLB nonlinear transitions better predict a wide range of functional motions
We assessed the nonlinear transitions computed by NOLB against 132 pairs of experimentally determined structures displaying a wide range of biologically relevant conformational changes. The RMSD between the two structures ranges from 0.5 to 33 Å, and the motions involve up to 80% of the protein atoms. For each pair, we defined a starting structure and a target structure. For a subset of 23 pairs (open-closed set, see below), each structure alternatively played the role of the starting structure and the target structure, resulting in a total of 155 predicted transitions. The transitions were computed by deforming the starting structure along its lowest-frequency modes, with the mode amplitudes being inferred from the displacement between the starting and target structures (Materials and Methods, Eq. 13). This allows for obtaining the optimal (or close-to-optimal) transitions within our framework. Nevertheless, we should stress that the knowledge of the target structure is only used to determine the sense and extent of the deformation along each mode, not the modes themselves. Hence, our approach is markedly different from linear interpolation or other morphing approaches implemented in popular tools (37,64, 65, 66, 67, 68). We set the number of selected modes to 10 because it was shown to be sufficient to describe 90% of open-to-closed conformational transitions (43). Moreover, this allows for performing real-time calculations. To compute all transitions reported here, it took us less than 5 min with one iteration and ∼15 min with five iterations on a single CPU.
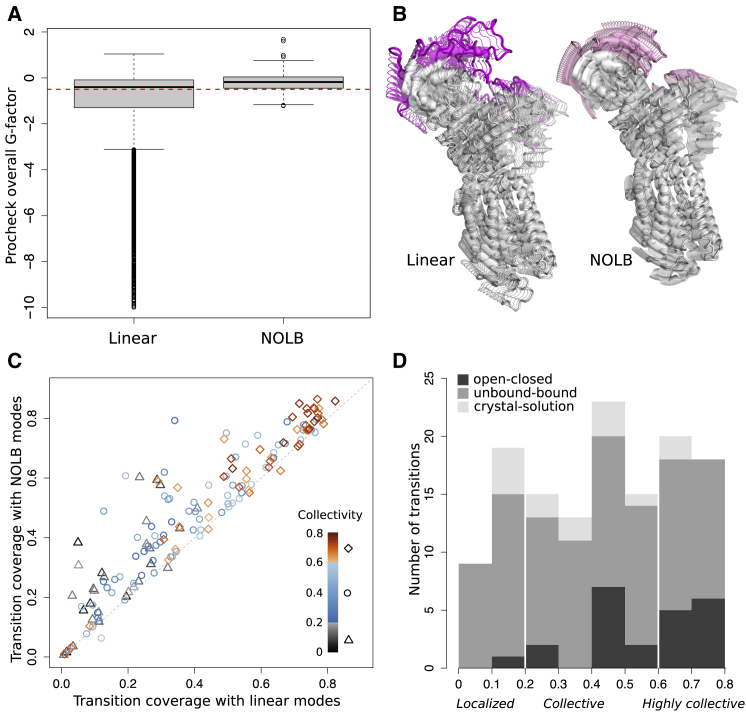
The quality of the conformations produced by NOLB was assessed by computing Procheck (46) G-factor (Fig. 2 A). A model resembling experimental structures deposited in the Protein Data Bank (PDB) should have a G-factor greater than −0.5 (red dotted line) and the higher the better. The vast majority of NOLB conformations are as good as an experimental structure. By comparison, the quality of the conformations produced by the classical linear extrapolation is much more variable, with a significant proportion displaying very low G-factors. Moreover, about three quarters of the predicted transitions are exclusively comprised of high-quality conformations when we use NOLB. This proportion drops to 21% when we use the classical linear extrapolation. Let us stress that seven (out of 155) transitions start from an experimental structure of poor quality (G-factor below −0.5). The better quality of the NOLB conformations can also be appreciated by directly looking at them and is particularly visible when dealing with large displacements. For instance, the calcium ATPase pump (PDB: 1su4-PDB: 1t5s) undergoes a large domain motion of 13.5 Å, taking place during active transport. Whereas the nonlinear transition computed by NOLB very well preserves the structure of the protein (Fig. 2 B, on the right, and see Video S1), the linear transition visibly distorts the cytoplasmic headpiece, where the closing motion takes place (Fig. 2 B, on the left, and see Video S2).
Figure 2.
Transition quality, coverage, and collectivity. (A) Shown is a comparison of the overall G-factors computed by Procheck on the conformations produced with the classical NMA (linear extrapolation) and with the NOLB method (nonlinear extrapolation). The distributions contain 7676 and 8769 conformations, respectively, corresponding to 155 transitions between 132 structure pairs (see text for details). (B) Shown is the closing of the calcium ATPase pump (PDB: 1su4-PDB: 1t5s). Conformations predicted by the classical NMA and by NOLB are shown on the left and the right, respectively. The residues undergoing the highest displacements are highlighted in color. (C) Shown is a comparison of the coverage achieved by the NOLB nonlinear modes with five iterations (y axis) versus the classical linear modes (x axis) for the 155 transitions. The colors indicate the degrees of collectivity of the experimental transitions. (D) Shown is a histogram of the collectivity degrees for all structure pairs from the three test sets. The transitions are labeled as localized (below 0.2), collective (between 0.2 and 0.6), and highly collective (above 0.6). To see this figure in color, go online.
The residues undergoing the highest displacements are highlighted in pink color and stick representation. This transition was produced using the command ”NOLB 1su4.pdb 1t5s.pdb -n 10 --nlin”.
The residues undergoing the highest displacements are highlighted in magenta color and stick representation. Please note unphysical scaling of the highlighted fragments with the progression of the transition. This transition was produced using the command ”NOLB 1su4.pdb 1t5s.pdb -n 10 --linear --trajectory -s 60”.
We also evaluated how close the final conformations produced by NOLB were to the target structures. For this, we computed the transition coverage (i.e., the relative RMSD between the initial and target structures explained by the predicted transition) (Materials and Methods, Eq. 16). To give an example, if the initial RMSD is of 5 Å, a prediction achieving a coverage of 70% will produce a final conformation 1.5 Å away from the target structure. On average, the NOLB predictions, computed with five iterations, covered 48% of the transitions. For comparison, the average coverage obtained with the classical linear modes was 40%. Moreover, the nonlinear predictions better approximated the transitions in 92% of the cases (Fig. 2 C). The superiority of the NOLB predictions was also found significant without any update of the modes along the transition (Fig. S1). Hence, beyond producing conformations with better stereochemical properties, the NOLB method also better exploits the information contained in the starting structure’s geometry to get closer to the target structure. The anticoagulation factor VIIa (Fig. 1, right panel, and Video S3) gives an illustrative example of a partner binding-associated large but localized transition (6.2 Å) that is clearly better described by NOLB. The transition involves a complex motion of an “arm” comprising ∼20% of the protein. The classical linear modes covered one third of the transition, producing a conformation 4.1 Å away from the target. The nonlinear NOLB normal modes achieved 44% coverage (Fig. 1, conformations in orange) and 79% after updating the modes three times (conformations in red). The final conformation is only 1.3 Å away from the target.
The starting and target structures are colored in grey and black, respectively. The part of the transition in orange is obtained from the normal modes computed on the starting structure. The part in red is obtained by updating the modes three times. This transition was produced using the command “NOLB 1fak_r_u.pdb 1fak_r_b.pdb -n 10 --nlin --nIter 3 -m”.
Noticeably, eight transitions are poorly predicted by classical NMA and by NOLB iterative scheme (coverage below 3.5%, see the points on the diagonal on Fig. 2 C). The majority of these cases (five out of eight) correspond to very small transitions (see also below). Visual inspection revealed that two of the remaining cases may be explained by ambiguities or errors in the experimental data (transitions involving the C-α only 4.2 Å resolution cryo-EM structure PDB: 3cau), and one case displays drastic rearrangements that linear and nonlinear normal modes fail to describe correctly. Let us stress that we did not observe any significant correlation between the transition coverage and the resolution of the starting and/or final structure(s) (Fig. S2).
NOLB extends the applicability of the NMA to localized motions
We collected the pairs of experimental structures from three benchmark sets designed for different practical applications, namely NMA, docking, and cryo-EM fitting. The first set comprises 23 proteins undergoing opening/closing motions. The vast majority of these transitions involve more than 40% of the protein atoms (Fig. 2 D, dark gray bars). They can be explained by a few low-frequency normal modes (typically 1–3) computed from the open form (Fig. 3 A, see bars in blue tones on the left). The second set contains 95 structural transitions associated with the binding of a protein partner. Such transitions are particularly challenging for protein docking applications (19,20,22,54,69,70). Indeed, they are often induced by the spatial proximity of the partner (induced-fit mechanism), which makes them very difficult to estimate starting only from the knowledge of the unbound state. This set includes a great variety of motions, from highly localized to highly collective ones (Fig. 2 D, medium gray bars). The transition coverage achieved by the classical linear normal modes is rather low (below 40%) for the majority of transitions (Fig. 3 B, see colored bars). The few transitions explained by the first three modes (see right part of the plot) involve more than 70% of the protein atoms and are all antibodies. The third set comprises 14 transitions between either a crystal structure and a solution structure solved by cryo-EM or between two cryo-EM solution structures (Table S1). Contrary to the other two sets, it is dominated by very small transitions, even below 1 Å (Fig. S3). The explanative power of the 10 first modes is very poor on this set (Fig. 3 C, left panel). Using 40 active modes significantly improves the coverage (Fig. 3 C, right panel). Nonetheless, the small transitions remain difficult to predict.
Figure 3.
Comparison of the transition coverages achieved on the three benchmark sets. The strips on top show Cα RMSD between the two known structures. The y axes show the transition coverage achieved by the 10 lowest-frequency linear normal modes (bars in blue tones), the NOLB nonlinear normal modes (in orange), and the NOLB nonlinear iterative scheme (in red). The x axes list the PDB codes, ordered according the NOLB normal mode predictions’ quality. (A) Open-to-closed (on the left) and closed-to-open (on the right) transitions are shown. (B) Unbound-to-bound transitions are shown. (C) Crystal-to-solution transitions are shown. The plot on the right shows the improvement of the predictions when increasing the number of active normal modes from 10 to 40. To see this figure in color, go online.
Overall, the ability of the classical NMA to predict transitions is largely determined by the transitions’ collectivity degrees (Fig. 2 C, see the color gradient along the x axis). Highly collective motions tend to be very well predicted, whereas localized motions tend to be poorly predicted, in agreement with previous works (29,36,57). We found that our nonlinear scheme permits to go beyond this observation and extends the applicability of the NMA. Indeed, the highest improvement of NOLB predictions over the classical NMA is observed for localized transitions, involving less than 20% of the protein atoms (Fig. 2 C, gray dots). The transition coverage is more than twice as big, on average, reaching a maximal value of 60% (vs. 40% for the linear normal modes). As illustrative examples, let us mention ephrin B4 receptor (PDB: 2hle:r), cysteine protease (PDB: 1pxv:r), actin (PDB: 1atn:r and PDB: 2btf:r), and rabex-5 VPS9 domain (PDB: 2ot3:l), which undergo localized motions upon binding to their partners (Fig. 3 B, see the location of the orange and red segments). Whereas the linear modes predict between 23 and 36% of their transitions, our nonlinear scheme predicts between 43 and 60% of them. The linear and nonlinear transitions predicted for actin are illustrated in Fig. 4 A (in blue and orange, see also Videos S4 and S5).
Figure 4.
Examples of predictions and random sampling assessment. (A and B) Shown is the superimposition of the predicted conformations (in color) onto the known starting (in gray) and target (in black) structures. The conformations in blue were produced by classical NMA, whereas those in other colors were produced by NOLB. The amplitude of the modes were either determined using the knowledge of the target state (on the left and in the middle) or randomly sampled (on the right, with colors matching (C)). (A) Shown is the transition of actin upon binding to DNase I (PDB: 1atn:r). The initial RMSD is 2.7 Å, and the motion involves 10% of the protein atoms. (B) Shown is the closing of the diaminopimelate dehydrogenase (PDB: 3dap–PDB: 1dap). The initial RMSD is 4.2 Å, and the motion involves about half of the protein atoms. (C) Shown are RMSDs computed between the 100 closest-to-target randomly sampled conformations and the target structure. In total, 10,000 conformations were generated for each protein. The proteins are split into two groups, depending on the type of transition. Within each group, they are ordered according to the RMSD between the starting and target structures, indicated by the colored dots. The x axis lists the PDB codes. To see this figure in color, go online.
The starting and target structures are colored in grey and black, respectively. The transition obtained with the classical linear modes is colored in blue. Please note the incorrect size of the loop that increases with the progression of the transition. This transition was produced using the command ”NOLB 1atn_r_u.pdb 1atn_r_b.pdb -n 10 --linear --trajectory -s 33”.
The starting and target structures are colored in grey and black, respectively. The transition obtained with NOLB nonlinear modes is colored in orange. This transition was produced using the command ”NOLB 1atn_r_u.pdb 1atn_r_b.pdb -n 10 --nlin -m”.
Updating of the modes allows for relaxing the elastic network’s constraints
The transitions predicted by the classical NMA strongly depend on the geometrical shape of the starting structure. This is particularly visible on the first test set, in which the closed-to-open transitions are significantly worse than the open-to-closed ones (compare the two plots in Fig. 3 A). Moreover, the number of transitions explained (at more than 40%) by the first three modes reduces from 18 to 8 upon starting from the closed structure. This effect was observed previously (29) and has a clear physical explanation connected to the limitations of the elastic network model. Indeed, the low-frequency modes are a consequence of the shape of the protein, and the shape of an open structure provides more information about its dynamical potential.
By recomputing the modes along the transition, our iterative scheme permits to overcome this limitation. Namely, it increases the coverage in the closed-to-open direction from 53 to 61%, on average (Fig. 3 A, see the location of the red segments on the right). This result can be explained by the fact that at each iteration, some elastic links are removed, alleviating some of the constraints that are exerted on the closed structure. As a consequence, the discrepancy between open-to-closed and closed-to-open predictions is largely reduced (compare the left and right plots). In four cases, namely the aspartate amino transferase (PDB: 9aat-PDB: 1ama), the maltodextrin binding protein (PDB: 1omp–PDB: 1anf), the alcohol dehydrogenase (PDB: 8adh–PDB: 2jhf), and the guanylate kinase (PDB: 1ex6–PDB: 1ex7), the coverage achieved in the two directions even becomes equivalent. The highest increase in coverage is obtained for the diaminopimelate dehydrogenase (PDB: 1dap–PDB: 3dap), from 31% without any update to 54% after one update (see Video S6).
The starting and target structures are colored in grey and black, respectively. The part of the transition in orange is obtained from the normal modes computed on the starting structure. The part in red is obtained by updating the modes five times. This transition was produced using the command ”NOLB 1dap.pdb 3dap.pdb -n 10 --nlin --nIter 5 -m”.
NOLB recapitulates known intermediates
Beyond stereochemical realism, we investigated whether the transitions predicted by NOLB could recapitulate known intermediate states. We selected four proteins undergoing large conformational transitions (6 Å) for which at least one intermediate structure is known (Fig. 5). Three of these proteins were previously studied in similar contexts (62,64). We recorded the RMSD from the experimental structures along the predicted transitions (Fig. 5, A–D) and quantified the extent to which these transitions spontaneously approached the known intermediate states by computing the improvement measure proposed in (62) (Materials and Methods, Eq. 17). It reflects the relative improvement of the predicted transition in recapitulating a given intermediate structure, compared to the starting and target structures.
Figure 5.
Prediction of transitions with known intermediates. (A) Bacterial ribose binding protein is shown. (B) Bacterial 5′-nucleotidase is shown. (C) Mammalian calcium ATPase pump is shown. (D and E) HSP90 homologs from bacteria (HTPG, PDB: 2ioq), yeast (HSP82, PDB: 2cg9), and mammals (GRP94, PDB: 2o1u) are shown. The transitions were predicted with five iterations of NOLB. (A–D) RMSD computed along the predicted transition with respect to some experimental structures is shown. The gray and red curves correspond to the starting and target structures, respectively, whereas the curves in blue tones correspond to intermediate structures. The dots indicate the predicted conformations being the closest to the intermediate states. (E) Shown is the superimposition of predicted conformations (in colored cartoons) onto experimental structures (in transparent gray surface) for HSP90. To see this figure in color, go online.
For the ribose binding protein, the NOLB transition allowed for reaching the two intermediate states and the target state with a deviation smaller than 1 Å (Fig. 5 A). The improvements are of 56 and 69% for the first and second intermediates, respectively. For the 5′-nucleotidase, NOLB produced conformations less than 2 Å away from the intermediate structures and covered 75% of the complete 9-Å transition (Fig. 5 B). The two intermediates are very similar, and the improvement is in the 54–57% range. For the calcium ATPase pump, we focused on the transition from the open E1-2Ca2+ state, with a splayed headpiece, to the closed headpiece ATP-bound E1-2Ca2+ state (Fig. 2 B). NOLB covered 76% of the transition, with a final RMSD to the target structure of 3.3 Å, and produced conformations ∼4 Å away from sarcolipin-bound E1-Mg2+ structures (Fig. 5 C). The latter might represent distorted intermediates due to the presence of sarcolipin, known to interfere with the transition by stabilizing the E1-Mg2+ state (71). This may explain the fact that the predicted conformations remain relatively distant from them, with improvement values of 19 and 26%.
Our last case study is that of the chaperone HSP90, which undergoes dramatic conformational changes upon binding to nucleotides. Many states have been characterized, but for some of them, only small angle x-ray scattering-based or electron microscopy-based low-resolution models are available. Here, we considered three crystallographic structures of HSP90 homologs, suggested to correspond to different steps in the conformational cycle of the chaperone (72). NOLB covers 63% of the transition from the starting open apo structure to the target closed ATP-bound structure and approaches a semiopen ADP-bound structure along the way (Fig. 5 D). The latter was suggested to represent an intermediate between the two others or a noncatalytic conformation (72). Although NOLB conformations remain relatively far from this structure (∼12 Å away), it is significantly closer than the two extreme structures, with an improvement of 29%. We should stress that this case is particularly challenging as the transition is of several tens of Å, and we are dealing with proteins coming from different organisms and sharing ∼40% sequence identity. Sequence divergence may be accompanied by local conformational rearrangements, increasing the RMSD. Visual inspection of the conformations shows a good match with the experimental structures (Fig. 5 E).
NOLB produces near-target conformations by random sampling
In the general case, the target is not known, and one has to sample the amplitudes of the modes. In most of the practical applications, however, the sampling is guided by additional information, which can be docking scores, small-angle scattering profiles, cryo-EM envelopes, cross-linking constraints, etc. To test whether this case could be dealt with in practice, we devised a conformational sampling strategy and applied it to a subset of 29 proteins from our data sets (Fig. 4). These proteins either display collective or highly collective transitions that are very well predicted (>70% coverage with NOLB) or localized motions poorly described by the linear modes (<30%) but well described by our iterative scheme (>40%). For each protein, we generated 10,000 conformations by progressively deforming the starting structure along its slowest normal modes using NOLB. The relative amplitudes of the modes were randomly sampled and fitted to a given RMSD. The simulation was decomposed into two or three steps, depending on the expected extent of the deformation (Materials and Methods). The first step performs most of the expected displacement using only the three slowest modes. For large transitions (4.5Å), an additional second step is performed using five modes and a smaller displacement. The final step consists of exploring the space around the previously generated conformations within 1 Å and exploiting all 10 slowest modes.
Depending on the protein, the simulation was able to produce conformations as close as 0.8–3 Å to the target structure (Fig. 4 C). Moreover, for a large majority of proteins (22 out of 29), the simulation produced several conformations with deviations smaller than 2 Å. The localized motions are more difficult to recapitulate than the collective ones (Fig. 4 C, compare left and right subpanels), but some generated conformations are still as close as 1.3–1.8 Å to the target. For instance, the closest-to-target conformation generated for actin (PDB: 1atn:r) deviates by 1.3 Å from the target (Fig. 4 A, green). This is better than the conformation produced by target-informed classical NMA (1.9 Å, blue) and only slightly worse than that produced by target-informed NOLB (1.1 Å, orange). For the collective transitions, there is a clear tendency for further away targets to be more difficult to reach (Fig. 4 C, see the correlation between the bars and dots color gradients). For example, in the case of carbon monoxide dehydrogenase (PDB: 1oao), the best conformation is found 2.9 Å away from the target state (Fig. 4 B, pink). This is ∼1.5 Å more than the conformations predicted using the knowledge of the target state (blue and orange). Nevertheless, we can see that the randomly sampled conformation superimposes well onto the target structure and recapitulates most of the transition. We performed four additional simulations replicates for each protein using different random seeds for sampling the modes’ amplitudes, and they produced similar results (Fig. S4).
CONCLUSION
This work revisits the formalism of normal modes and demonstrates its applicability to the previously inaccessible cases of localized motions. Specifically, it critically assesses the relevance of the NMA to the computation of various structural transitions in biological macromolecules. Our results challenge the long-standing belief that the lowest-frequency modes can only describe collective transitions. Indeed, we show that nonlinear normal modes can also approximate local deformations such as loop motions. Moreover, iterative recomputation of the normal modes relaxes constraints imposed by the geometry of the protein and allows for pushing the transitions even further. Another important advantage of our method is that the predicted conformations have a much better local geometry than those resulting from linear NMA perturbations. We demonstrated it by computing the quality of the transition intermediate states using the Procheck scores. We also showed that the predicted transitions recapitulate the known intermediate states solved experimentally and that we can predict the transitions by randomly sampling the amplitudes of the lowest normal modes.
Small structural changes, for example those present in the Cryo-EM 2015/2016 Model Challenge benchmark, still remain very difficult to predict with the NMA formalism. Indeed, in this case, adding nonlinearity and iterative computations did not improve the results significantly. Activating a much larger number of modes can help with approximating the transitions but at the expense of a significant computational cost. Indeed, the full diagonalization of the Hessian matrix scales as O(N3) with the number of degrees of freedom N. Therefore, it becomes preferable to use MD-based or other stochastic optimization techniques (i.e., simulated annealing), with the full range of degrees of freedom.
Our method is very CPU and memory efficient—it took us ∼9 min to compute the nonlinear structural transitions for all proteins from the PPDBv5 (460 in total) set on a desktop computer. This implies that the method can be applied on a very large scale. For instance, it can be used to model flexibility in docking calculations or to generate putative conformations that can be targeted by small molecules.
Author Contributions
A.H. developed the diagonalization scheme. S.G. proposed the twist method and coded the algorithm. E.L. performed the tests and plotted the figures. S.G. and E.L. wrote the manuscript. S.G. and E.L. contributed equally to this work.
Acknowledgments
This work was partially funded by a grant of the French national research agency (MASSIV project, ANR-17-CE12-0009).
Editor: Monika Fuxreiter.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.03.020.
Supporting Material
References
- 1.Berman H.M., Westbrook J., Bourne P.E. The protein data bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Callaway E. The revolution will not be crystallized: a new method sweeps through structural biology. Nature. 2015;525:172–174. doi: 10.1038/525172a. [DOI] [PubMed] [Google Scholar]
- 3.Hayward S., Go N. Collective variable description of native protein dynamics. Annu. Rev. Phys. Chem. 1995;46:223–250. doi: 10.1146/annurev.pc.46.100195.001255. [DOI] [PubMed] [Google Scholar]
- 4.Tama F., Miyashita O., Brooks C.L., III Normal mode based flexible fitting of high-resolution structure into low-resolution experimental data from cryo-EM. J. Struct. Biol. 2004;147:315–326. doi: 10.1016/j.jsb.2004.03.002. [DOI] [PubMed] [Google Scholar]
- 5.Tama F., Miyashita O., Brooks C.L., III Flexible multi-scale fitting of atomic structures into low-resolution electron density maps with elastic network normal mode analysis. J. Mol. Biol. 2004;337:985–999. doi: 10.1016/j.jmb.2004.01.048. [DOI] [PubMed] [Google Scholar]
- 6.Suhre K., Navaza J., Sanejouand Y.H. NORMA: a tool for flexible fitting of high-resolution protein structures into low-resolution electron-microscopy-derived density maps. Acta Crystallogr. D Biol. Crystallogr. 2006;62:1098–1100. doi: 10.1107/S090744490602244X. [DOI] [PubMed] [Google Scholar]
- 7.Schröder G.F., Brunger A.T., Levitt M. Combining efficient conformational sampling with a deformable elastic network model facilitates structure refinement at low resolution. Structure. 2007;15:1630–1641. doi: 10.1016/j.str.2007.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schröder G.F., Levitt M., Brunger A.T. Super-resolution biomolecular crystallography with low-resolution data. Nature. 2010;464:1218–1222. doi: 10.1038/nature08892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tan R.K., Devkota B., Harvey S.C. YUP.SCX: coaxing atomic models into medium resolution electron density maps. J. Struct. Biol. 2008;163:163–174. doi: 10.1016/j.jsb.2008.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zheng W. Accurate flexible fitting of high-resolution protein structures into cryo-electron microscopy maps using coarse-grained pseudo-energy minimization. Biophys. J. 2011;100:478–488. doi: 10.1016/j.bpj.2010.12.3680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lopéz-Blanco J.R., Chacón P. iMODFIT: efficient and robust flexible fitting based on vibrational analysis in internal coordinates. J. Struct. Biol. 2013;184:261–270. doi: 10.1016/j.jsb.2013.08.010. [DOI] [PubMed] [Google Scholar]
- 12.Gorba C., Miyashita O., Tama F. Normal-mode flexible fitting of high-resolution structure of biological molecules toward one-dimensional low-resolution data. Biophys. J. 2008;94:1589–1599. doi: 10.1529/biophysj.107.122218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kondrashov D.A., Van Wynsberghe A.W., Phillips G.N., Jr. Protein structural variation in computational models and crystallographic data. Structure. 2007;15:169–177. doi: 10.1016/j.str.2006.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhou L., Liu Q. Aligning experimental and theoretical anisotropic B-factors: water models, normal-mode analysis methods, and metrics. J. Phys. Chem. B. 2014;118:4069–4079. doi: 10.1021/jp4124327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cavasotto C.N., Kovacs J.A., Abagyan R.A. Representing receptor flexibility in ligand docking through relevant normal modes. J. Am. Chem. Soc. 2005;127:9632–9640. doi: 10.1021/ja042260c. [DOI] [PubMed] [Google Scholar]
- 16.Mustard D., Ritchie D.W. Docking essential dynamics eigenstructures. Proteins. 2005;60:269–274. doi: 10.1002/prot.20569. [DOI] [PubMed] [Google Scholar]
- 17.Emekli U., Schneidman-Duhovny D., Haliloglu T. HingeProt: automated prediction of hinges in protein structures. Proteins. 2008;70:1219–1227. doi: 10.1002/prot.21613. [DOI] [PubMed] [Google Scholar]
- 18.Schneidman-Duhovny D., Nussinov R., Wolfson H.J. Automatic prediction of protein interactions with large scale motion. Proteins. 2007;69:764–773. doi: 10.1002/prot.21759. [DOI] [PubMed] [Google Scholar]
- 19.Moal I.H., Bates P.A. SwarmDock and the use of normal modes in protein-protein docking. Int. J. Mol. Sci. 2010;11:3623–3648. doi: 10.3390/ijms11103623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fiorucci S., Zacharias M. Binding site prediction and improved scoring during flexible protein-protein docking with ATTRACT. Proteins. 2010;78:3131–3139. doi: 10.1002/prot.22808. [DOI] [PubMed] [Google Scholar]
- 21.May A., Zacharias M. Energy minimization in low-frequency normal modes to efficiently allow for global flexibility during systematic protein-protein docking. Proteins. 2008;70:794–809. doi: 10.1002/prot.21579. [DOI] [PubMed] [Google Scholar]
- 22.Neveu E., Popov P., Grudinin S. RapidRMSD: rapid determination of RMSDs corresponding to motions of flexible molecules. Bioinformatics. 2018;34:2757–2765. doi: 10.1093/bioinformatics/bty160. [DOI] [PubMed] [Google Scholar]
- 23.Delarue M., Dumas P. On the use of low-frequency normal modes to enforce collective movements in refining macromolecular structural models. Proc. Natl. Acad. Sci. USA. 2004;101:6957–6962. doi: 10.1073/pnas.0400301101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lindahl E., Azuara C., Delarue M. NOMAD-ref: visualization, deformation and refinement of macromolecular structures based on all-atom normal mode analysis. Nucleic Acids Res. 2006;34:W52–W56. doi: 10.1093/nar/gkl082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lindahl E., Delarue M. Refinement of docked protein-ligand and protein-DNA structures using low frequency normal mode amplitude optimization. Nucleic Acids Res. 2005;33:4496–4506. doi: 10.1093/nar/gki730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mashiach E., Nussinov R., Wolfson H.J. FiberDock: flexible induced-fit backbone refinement in molecular docking. Proteins. 2010;78:1503–1519. doi: 10.1002/prot.22668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Venkatraman V., Ritchie D.W. Flexible protein docking refinement using pose-dependent normal mode analysis. Proteins. 2012;80:2262–2274. doi: 10.1002/prot.24115. [DOI] [PubMed] [Google Scholar]
- 28.Ma J. Usefulness and limitations of normal mode analysis in modeling dynamics of biomolecular complexes. Structure. 2005;13:373–380. doi: 10.1016/j.str.2005.02.002. [DOI] [PubMed] [Google Scholar]
- 29.Tama F., Sanejouand Y.H. Conformational change of proteins arising from normal mode calculations. Protein Eng. 2001;14:1–6. doi: 10.1093/protein/14.1.1. [DOI] [PubMed] [Google Scholar]
- 30.Bonomi M., Pellarin R., Vendruscolo M. Simultaneous determination of protein structure and dynamics using cryo-electron microscopy. Biophys. J. 2018;114:1604–1613. doi: 10.1016/j.bpj.2018.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Amadei A., Linssen A.B., Berendsen H.J. Essential dynamics of proteins. Proteins. 1993;17:412–425. doi: 10.1002/prot.340170408. [DOI] [PubMed] [Google Scholar]
- 32.Stepanova M. Dynamics of essential collective motions in proteins: theory. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;76:051918. doi: 10.1103/PhysRevE.76.051918. [DOI] [PubMed] [Google Scholar]
- 33.Spiwok V., Lipovová P., Králová B. Metadynamics in essential coordinates: free energy simulation of conformational changes. J. Phys. Chem. B. 2007;111:3073–3076. doi: 10.1021/jp068587c. [DOI] [PubMed] [Google Scholar]
- 34.Fiorin G., Klein M.L., Hénin J. Using collective variables to drive molecular dynamics simulations. Mol. Phys. 2013;111:3345–3362. [Google Scholar]
- 35.Hoffmann A., Grudinin S. NOLB: nonlinear rigid block normal-mode analysis method. J. Chem. Theory Comput. 2017;13:2123–2134. doi: 10.1021/acs.jctc.7b00197. [DOI] [PubMed] [Google Scholar]
- 36.Mendez R., Bastolla U. Torsional network model: normal modes in torsion angle space better correlate with conformation changes in proteins. Phys. Rev. Lett. 2010;104:228103. doi: 10.1103/PhysRevLett.104.228103. [DOI] [PubMed] [Google Scholar]
- 37.López-Blanco J.R., Aliaga J.I., Chacón P. iMODS: internal coordinates normal mode analysis server. Nucleic Acids Res. 2014;42:W271–W276. doi: 10.1093/nar/gku339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Frezza E., Lavery R. Internal normal mode analysis (iNMA) applied to protein conformational flexibility. J. Chem. Theory Comput. 2015;11:5503–5512. doi: 10.1021/acs.jctc.5b00724. [DOI] [PubMed] [Google Scholar]
- 39.Noguti T., Gõ N. Dynamics of native globular proteins in terms of dihedral angles. J. Phys. Soc. Jpn. 1983;52:3283–3288. [Google Scholar]
- 40.Levitt M., Sander C., Stern P.S. Protein normal-mode dynamics: trypsin inhibitor, crambin, ribonuclease and lysozyme. J. Mol. Biol. 1985;181:423–447. doi: 10.1016/0022-2836(85)90230-x. [DOI] [PubMed] [Google Scholar]
- 41.Kamiya K., Sugawara Y., Umeyama H. Algorithm for normal mode analysis with general internal coordinates. J. Comput. Chem. 2003;24:826–841. doi: 10.1002/jcc.10247. [DOI] [PubMed] [Google Scholar]
- 42.Lu M., Poon B., Ma J. A new method for coarse-grained elastic normal-mode analysis. J. Chem. Theory Comput. 2006;2:464–471. doi: 10.1021/ct050307u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lopéz-Blanco J.R., Garzón J.I., Chacón P. iMod: multipurpose normal mode analysis in internal coordinates. Bioinformatics. 2011;27:2843–2850. doi: 10.1093/bioinformatics/btr497. [DOI] [PubMed] [Google Scholar]
- 44.Vreven T., Moal I.H., Weng Z. Updates to the integrated protein-protein interaction benchmarks: docking benchmark version 5 and affinity benchmark version 2. J. Mol. Biol. 2015;427:3031–3041. doi: 10.1016/j.jmb.2015.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lawson C., Kryshtafovych A., Sala R. 2018. CryoEM models and associated data submitted to the 2015/2016 EMDataBank model challenge. Zenodo. [DOI] [Google Scholar]
- 46.Laskowski R.A., MacArthur M.W., Thornton J.M. PROCHECK: a program to check the stereochemical quality of protein structures. J. Appl. Cryst. 1993;26:283–291. [Google Scholar]
- 47.Tirion M.M. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 1996;77:1905–1908. doi: 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
- 48.Krebs W.G., Alexandrov V., Gerstein M. Normal mode analysis of macromolecular motions in a database framework: developing mode concentration as a useful classifying statistic. Proteins. 2002;48:682–695. doi: 10.1002/prot.10168. [DOI] [PubMed] [Google Scholar]
- 49.Durand P., Trinquier G., Sanejouand Y.-H. A new approach for determining low-frequency normal modes in macromolecules. Biopolymers. 1994;34:759–771. [Google Scholar]
- 50.Tama F., Gadea F.X., Sanejouand Y.H. Building-block approach for determining low-frequency normal modes of macromolecules. Proteins. 2000;41:1–7. doi: 10.1002/1097-0134(20001001)41:1<1::aid-prot10>3.0.co;2-p. [DOI] [PubMed] [Google Scholar]
- 51.Tekpinar M. Flexible fitting to cryo-electron microscopy maps with coarse-grained elastic network models. Mol. Simulat. 2018;44:688–696. [Google Scholar]
- 52.Echols N., Milburn D., Gerstein M. MolMovDB: analysis and visualization of conformational change and structural flexibility. Nucleic Acids Res. 2003;31:478–482. doi: 10.1093/nar/gkg104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Chen V.B., Arendall W.B., III, Richardson D.C. MolProbity: all-atom structure validation for macromolecular crystallography. Acta Crystallogr. D Biol. Crystallogr. 2010;66:12–21. doi: 10.1107/S0907444909042073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Dobbins S.E., Lesk V.I., Sternberg M.J. Insights into protein flexibility: the relationship between normal modes and conformational change upon protein-protein docking. Proc. Natl. Acad. Sci. USA. 2008;105:10390–10395. doi: 10.1073/pnas.0802496105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Li G., Cui Q. A coarse-grained normal mode approach for macromolecules: an efficient implementation and application to Ca(2+)-ATPase. Biophys. J. 2002;83:2457–2474. doi: 10.1016/S0006-3495(02)75257-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Song G., Jernigan R.L. An enhanced elastic network model to represent the motions of domain-swapped proteins. Proteins. 2006;63:197–209. doi: 10.1002/prot.20836. [DOI] [PubMed] [Google Scholar]
- 57.Yang L., Song G., Jernigan R.L. How well can we understand large-scale protein motions using normal modes of elastic network models? Biophys. J. 2007;93:920–929. doi: 10.1529/biophysj.106.095927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Doruker P., Atilgan A.R., Bahar I. Dynamics of proteins predicted by molecular dynamics simulations and analytical approaches: application to alpha-amylase inhibitor. Proteins. 2000;40:512–524. [PubMed] [Google Scholar]
- 59.Atilgan A.R., Durell S.R., Bahar I. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 2001;80:505–515. doi: 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Bahar I., Lezon T.R., Shrivastava I.H. Normal mode analysis of biomolecular structures: functional mechanisms of membrane proteins. Chem. Rev. 2010;110:1463–1497. doi: 10.1021/cr900095e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Artemova S., Grudinin S., Redon S. A comparison of neighbor search algorithms for large rigid molecules. J. Comput. Chem. 2011;32:2865–2877. doi: 10.1002/jcc.21868. [DOI] [PubMed] [Google Scholar]
- 62.Weiss D.R., Levitt M. Can morphing methods predict intermediate structures? J. Mol. Biol. 2009;385:665–674. doi: 10.1016/j.jmb.2008.10.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Brüschweiler R. Collective protein dynamics and nuclear spin relaxation. J. Chem. Phys. 1995;102:3396–3403. [Google Scholar]
- 64.Orellana L., Yoluk O., Lindahl E. Prediction and validation of protein intermediate states from structurally rich ensembles and coarse-grained simulations. Nat. Commun. 2016;7:12575. doi: 10.1038/ncomms12575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Koehl P. Minimum action transition paths connecting minima on an energy surface. J. Chem. Phys. 2016;145:184111. doi: 10.1063/1.4966974. [DOI] [PubMed] [Google Scholar]
- 66.Franklin J., Koehl P., Delarue M. MinActionPath: maximum likelihood trajectory for large-scale structural transitions in a coarse-grained locally harmonic energy landscape. Nucleic Acids Res. 2007;35:W477–W482. doi: 10.1093/nar/gkm342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Miyashita O., Onuchic J.N., Wolynes P.G. Nonlinear elasticity, proteinquakes, and the energy landscapes of functional transitions in proteins. Proc. Natl. Acad. Sci. USA. 2003;100:12570–12575. doi: 10.1073/pnas.2135471100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Nguyen M.K., Jaillet L., Redon S. Generating conformational transition paths with low potential-energy barriers for proteins. J. Comput. Aided Mol. Des. 2018;32:853–867. doi: 10.1007/s10822-018-0137-7. [DOI] [PubMed] [Google Scholar]
- 69.Neveu E., Ritchie D.W., Grudinin S. PEPSI-dock: a detailed data-driven protein-protein interaction potential accelerated by polar Fourier correlation. Bioinformatics. 2016;32:i693–i701. doi: 10.1093/bioinformatics/btw443. [DOI] [PubMed] [Google Scholar]
- 70.Marsh J.A., Teichmann S.A., Forman-Kay J.D. Probing the diverse landscape of protein flexibility and binding. Curr. Opin. Struct. Biol. 2012;22:643–650. doi: 10.1016/j.sbi.2012.08.008. [DOI] [PubMed] [Google Scholar]
- 71.Toyoshima C., Iwasawa S., Inesi G. Crystal structures of the calcium pump and sarcolipin in the Mg2+-bound E1 state. Nature. 2013;495:260–264. doi: 10.1038/nature11899. [DOI] [PubMed] [Google Scholar]
- 72.Krukenberg K.A., Street T.O., Agard D.A. Conformational dynamics of the molecular chaperone Hsp90. Q. Rev. Biophys. 2011;44:229–255. doi: 10.1017/S0033583510000314. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The residues undergoing the highest displacements are highlighted in pink color and stick representation. This transition was produced using the command ”NOLB 1su4.pdb 1t5s.pdb -n 10 --nlin”.
The residues undergoing the highest displacements are highlighted in magenta color and stick representation. Please note unphysical scaling of the highlighted fragments with the progression of the transition. This transition was produced using the command ”NOLB 1su4.pdb 1t5s.pdb -n 10 --linear --trajectory -s 60”.
The starting and target structures are colored in grey and black, respectively. The part of the transition in orange is obtained from the normal modes computed on the starting structure. The part in red is obtained by updating the modes three times. This transition was produced using the command “NOLB 1fak_r_u.pdb 1fak_r_b.pdb -n 10 --nlin --nIter 3 -m”.
The starting and target structures are colored in grey and black, respectively. The transition obtained with the classical linear modes is colored in blue. Please note the incorrect size of the loop that increases with the progression of the transition. This transition was produced using the command ”NOLB 1atn_r_u.pdb 1atn_r_b.pdb -n 10 --linear --trajectory -s 33”.
The starting and target structures are colored in grey and black, respectively. The transition obtained with NOLB nonlinear modes is colored in orange. This transition was produced using the command ”NOLB 1atn_r_u.pdb 1atn_r_b.pdb -n 10 --nlin -m”.
The starting and target structures are colored in grey and black, respectively. The part of the transition in orange is obtained from the normal modes computed on the starting structure. The part in red is obtained by updating the modes five times. This transition was produced using the command ”NOLB 1dap.pdb 3dap.pdb -n 10 --nlin --nIter 5 -m”.