Maximum Entropy Optimized Force Field for Intrinsically Disordered Proteins

Abstract

Intrinsically disordered proteins (IDPs) constitute a significant fraction of eukaryotic proteomes. High-resolution characterization of IDP conformational ensembles can help elucidate their roles in a wide range of biological processes but remains challenging both experimentally and computationally. Here, we present a generic algorithm to improve the accuracy of coarse-grained IDP models using a diverse set of experimental measurements. It combines maximum entropy optimization and least squares regression to systematically adjust model parameters and improve the agreement between simulation and experiment. We successfully applied the algorithm to derive a transferable force field, which we term as MOFF, for de novo prediction of IDP structures. Statistical analysis of force field parameters reveals features of amino acid interactions not captured by potentials designed to work well for folded proteins. We anticipate its combination of efficiency and accuracy will make MOFF useful for studying the phase separation of IDPs, which drives the formation of various biological compartments.

Graphical Abstract

Introduction

The classical structure-function paradigm suggests that proteins must fold into unique three-dimensional conformations to perform their functions within the cell.^1,2 It has helped establish conceptual frameworks that are instrumental in understanding crucial biological features such as the enzymatic activity³ and protein evolution.⁴ However, recent evidence suggests that 30 to 40% of eukaryotic proteomes contain disordered regions that do not fold into defined tertiary structures.⁵ These so-called intrinsically disordered proteins (IDPs), instead, function with an ensemble of different conformations. They can promote liquid-liquid phase separation via multivalent interactions and are critical for the formation of cellular compartments such as stress granules, P granules, super-enhancers, and heterochromatin.^6–10 It has been argued that disorderness and multivalent interactions are indeed evolutionarily advantageous for performing increasingly more complicated tasks in higher-order organism.¹¹ An appreciation of this emerging disorder-function relationship for IDPs requires a detailed characterization of their structures and the set of physicochemical interactions that dictate their organization.^12–18

Though significant progress has been made, high-resolution structural characterization remains challenging for IDPs. In particular, traditional experimental techniques that found great success with folded proteins, such as X-Ray scattering and Cryo-electron microscopy, face difficulty in resolving the fuzzy conformation of IDPs.^19–21 The two popular techniques that are often used for studying IDPs are small-angle X-ray scattering (SAXS) and Förster resonance energy transfer (FRET).^22–25 Both are low-resolution approaches that fall short at providing detailed atomic structures. Recent developments in atomistic force fields have significantly improved the accuracy of all-atom computer simulations, rendering in silico prediction a promising approach to characterize the ensemble of IDP structures.^26–28 The computational cost associated with atomistic simulations, however, limits their application to single and small proteins.

For more efficient simulations of IDPs, numerous groups have developed coarse-grained protein models.^29–37 For example, the hydrophobicity scale model, introduced by Mittal and coworkers,^29–31 treats each residue as a single particle. Non-bonded interactions between the coarse-grained particles were parameterized based on amino acid hydrophobicity to reproduce protein radius of gyrations. The Thirumalai group adopted a self-organized polymer to model IDPs with two beads per amino acid.³⁴ Using the rescaled Betancourt-Thirumalai statistical potential³⁸ for amino acid interactions, they showed that the model can delineate the complex interplay between protein sequence and structure. Additionally, Papoian and coworkers generalized the associative memory, water-mediated, structure and energy model (AWSEM) model developed by the Wolynes group^36,39,40 for IDPs by reweighting the strength of secondary structure potentials and introducing a novel functional form to control protein size.³³ Finally, in the model, ABSINTH, introduced Pappu and coworkers, interactions between amino acids are modeled with atomistic detail and solvent effect is accounted for implicitly with a novel mean-field scheme.⁴¹ The expanded range of accessible timescales in these models is valuable for an exhaustive sampling of protein conformation and computing thermodynamic quantities.

Algorithms that can systematically parameterize coarse-grained models are of great interest and can further improve the accuracy of existing IDP models. Optimization methods based on the energy landscape theory,^42–46 which worked well for deriving force fields of globular proteins by maximizing the energy gap between folded and unfolded configurations,^47,48 are not applicable because IDPs, by definition, lack a unique folded structure. An alternative approach to further refine the accuracy of computational models for a specific protein is to incorporate additional experimental measurements.^49–51 For example, in Ref. 52, we demonstrated that a maximum entropy based algorithm can significantly improve the agreement between simulated and experimental small-angle X-ray scattering profiles by adding a linear biasing term to the model’s energy function. An obvious drawback of this algorithm is that it cannot be applied to proteins for which no experimental data is available.

In this paper, we generalize the maximum entropy algorithm introduced by us⁵² to parameterize a transferable force field for IDPs, which we term as maximum entropy optimized force field or MOFF. Instead of optimizing the energy gap as in folded proteins, the algorithm strives to reproduce the energy distribution for an ensemble of IDP configurations obtained from maximum entropy biasing. It involves iterations of maximum entropy optimization to derive biasing energies that reproduce experimental inputs, and least-squares fitting that converts the biasing energies into force field corrections. We demonstrate that MOFF is transferable and can be applied to predict protein structures de novo. Analysis of this force field further reveals amino acid interaction patterns not captured by statistical potentials that work well for folded proteins, explaining their lack of transferability for studying IDPs. As its quality can be continuously improved with the incorporation of more proteins and experimental measurements during parameterization, we anticipate MOFF to be useful for studying a wide range of problems related to IDPs.

Methods

Algorithm for force field parameterization

Numerous computational models and force fields have been proposed for IDPs, and they have provided molecular insight into a wide range of biological processes.^29–37 Parameters in these models were often derived with phenomenological approaches based on some biophysical properties and statistics of amino acids derived from folded proteins. Systematically improving upon them to provide a better characterization of IDPs remains non-trivial. In the following, we present an algorithm to refine IDP force fields for better agreement with experimental measurements. The hydrophobic scale (HPS) model introduced by Mittal and coworkers³⁰ was used as an example for illustration purposes, but the algorithm is general and can be directly applied to other force fields as well.

Our goal is to fine-tune force field parameters to improve the agreement between the simulated and experimental radius of gyrations (R_g) of IDPs. Here, we focus on R_g due to its availability for a broad set of proteins, but other experimental measurements can be incorporated as well. A promising approach for improving the agreement between simulation and experiment is to introduce maximum entropy biases to computational models.^49–51,53 The maximum entropy approach has gained wide popularity and been applied to a variety of problems due to its simplicity and fundamental connection to the information theory.^52,54–58 It suggests that for a given protein, to ensure that the R_g of simulated structures matches the experimental value, a linear bias should be added to the model Hamiltonian

$$U_{\text{ME}}(r)=U_{\text{HPS}}(r)+\alpha R_g(r),$$ (1)

where r represents protein configurations and U_HPS(r) is the energy function defined by the hydrophobicity scale model.³⁰

The maximum entropy approach can be applied to any protein and is guaranteed to reproduce experimental measurements. Its main drawback is that the resulting energy function is not transferable and a unique biasing energy αR_g(r) needs to be determined for every protein of interest. Such repeated parameterization can be cumbersome and becomes impractical for proteins with no experimental input. We introduce the maximum entropy optimized force field (MOFF) for transferable modeling of IDPs

$$U_{\text{MOFF}}(r)=U_{\text{HPS}}(r)+\sum _{I,J}{ϵ}_{IJ}{\mathcal{C}}_{IJ}(r)$$ (2)

where I and J indexes over different amino acid types. ${\mathcal{C}}_{IJ}(r)=\sum _{i\in I,j\in J}\mathcal{C}\left(r_{ij}\right)$ counts the number of contacts between amino acid types I and J within a protein configuration r. The contact function between a pair of amino acids i and j separated at a distance r_ij is defined as

$$\mathcal{C}\left(r_{ij}\right)=\frac{1}{2}\left(1+\text{tanh}\left[\eta \left(r_{\text{o}}-r_{ij}\right)\right]\right)$$ (3)

with r_o = 8 Å and η = 0.7 Å⁻¹. ϵ_IJ corresponds to the energetic cost for contact formation and their values will be derived from maximum entropy biases defined in Eq. 1 by solving the following set of linear equations

$$\sum _{I,J}{ϵ}_{IJ}{\mathcal{C}}_{IJ}\left(r_m\right)\equiv \alpha R_g\left(r_m\right)\text{\hspace{1em}for}m=1,\cdots ,M.$$ (4)

A total of M structures for a given protein can be used to provide a large set of variation of contacts for an efficient determination of the parameters.

To derive a transferable force field, however, several technical aspects need to be addressed. First, Eq. 4 needs to be generalized to include multiple proteins to ensure the transferability of ϵ_IJ. Second, there is an inherent conflict in Eq. 4, as the left and right side reaches 0 at different points. By definition, when there are no contacts, the left side of the equation is 0. However, in this limit, R_g is maximized, and the right side of the equation is at an extremum. We can resolve this apparent conflict by subtracting a reference point energy $\alpha R_g^{\text{exp}}$—the biasing energy at the experimental value—from both sides of the equation. This subtraction is justified by the realization that only energy differences are needed to reproduce the structural ensemble and the mean R_g, while the absolute energies are of no particular significance. Following Eq. 4, on the left hand side, we further converted the biasing energy into a linear combination of pair-wise contacts ${ϵ}_{IJ}{\mathcal{C}}_{IJ}^{n,\text{exp}}$. ${\mathcal{C}}_{IJ}^{\text{exp}}$ can be estimated using simulated protein structures with R_g values that are within 0.5 Å of the experimental measurement. The small deviation 0.5 Å was introduced to account for experimental error and to ensure statistical convergence with enough protein structures. Third, the quality of the force field depends on the assumption used in deriving Eq. 4 that the biasing energies can be approximated with a linear combination of pairwise contacts. The validity of this assumption may be poor, especially at large biasing energies. Accuracy of the linear approximation can be systematically improved by an iterative procedure in which we find maximum entropy biasing energies to the newly derived MOFF and use them to update force field parameters further. As the difference between model predictions and experimental measurements drops, the strength of the biasing energies will decrease, and the quality of the linear approximation will improve.

With all these factors accounted for, we solve the following equations iteratively to derive parameters for MOFF

$$\sum _{I,J}{ϵ}_{IJ}\left[{\mathcal{C}}_{IJ}\left(r_m^n\right)-{\mathcal{C}}_{IJ}^{n,\text{exp}}\right]\equiv {\alpha }_n\left[R_g\left(r_m^n\right)-R_g^{n,\text{exp}}\right],\text{\hspace{1em}for}m=1,\cdots ,M\text{and}n=1,\cdots ,N.$$ (5)

where n and m indexes over different proteins and the structures for a given protein. An illustration of the algorithm is provided in Figure 1.

Figure 1:

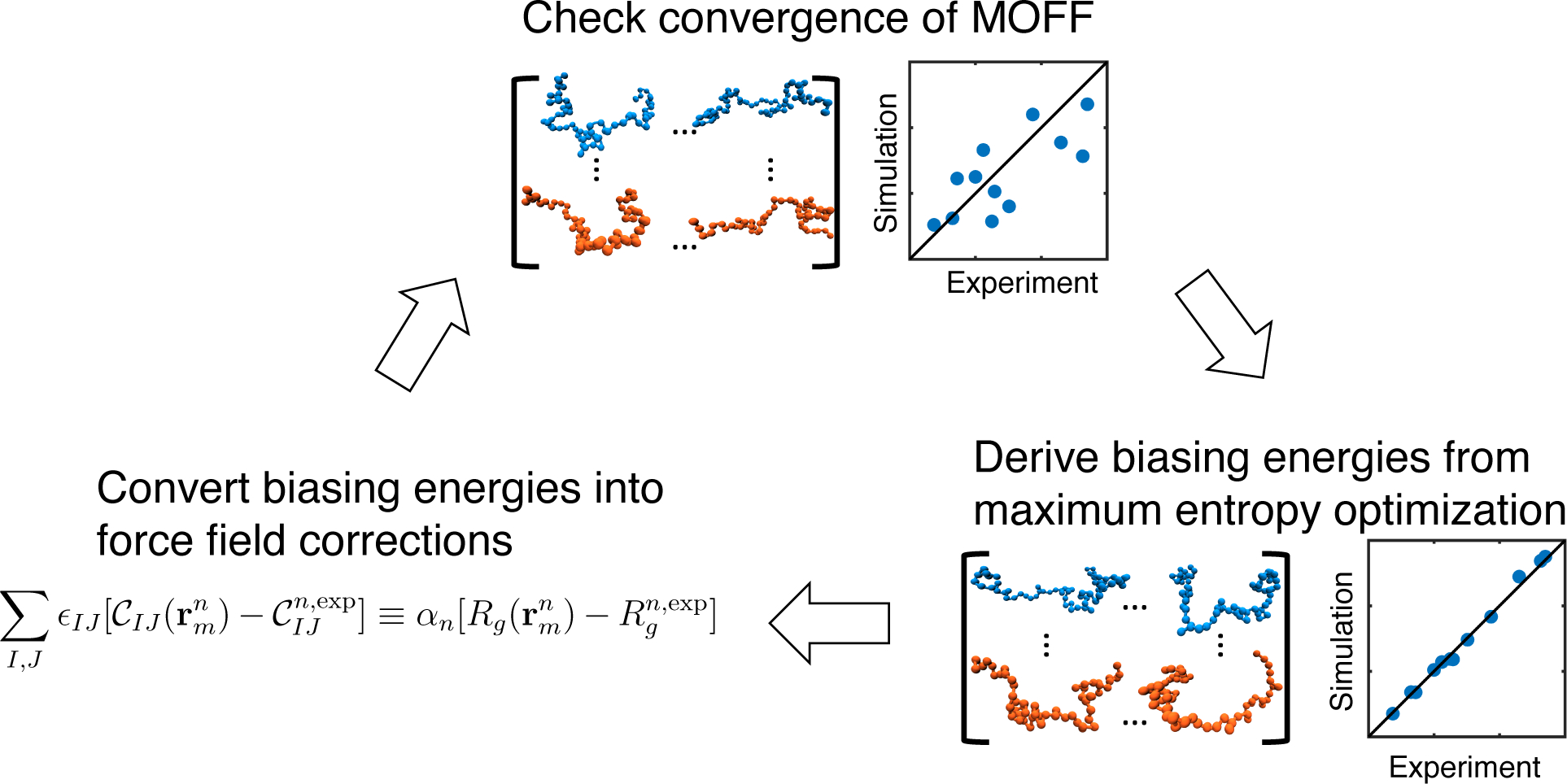
Illustration of the iterative algorithm for coarse grained force field optimization.

Solution to Eq. 5 can be found with least squares regression by recasting the equation in matrix form as

$$\mathit{ϵ}C\equiv R_{\mathit{g}},$$ (6)

where ϵ, C, and R_g are matrix versions of the contact energy, contact number, and bias energy respectively. We then solve for using least squares as

$$\mathit{ϵ}={\left(C^{T}C\right)}^{-1}{C}^T{R}_{\mathit{g}}.$$ (7)

To reduce statistical noise that originates from a finite sample of protein sequences and structures, we reconstructed C^T C with the largest 60% eigenvalues before calculating its inverse.

Hydrophobic scale model of IDP

As aforementioned, we used the hydrophobicity scale model as the starting point for our force field refinement.^29–31 Protein molecules in this model are described at the residue level, with one bead for each α-carbon. Interactions between amino acids were parameterized based on their hydrophobicity with a multiplicative scaling factor.

The energy function of this model consists of three terms and

$$U_{\text{HPS}}(r)=U_{\text{b}}(r)+U_{\text{e}}(r)+U_{\text{nb}}(r).$$ (8)

U_b(r) is the bonding energy between adjacent amino acids and is modeled using a harmonic potential with a spring constant of 10 kJ/mol/Ų and a bond length of 3.8 Å. U_e(r) corresponds to electrostatic interactions between charged residues modeled at the Debye-Hückle level. We used = 80 for the dielectric constant of water, and the ionic strength was set individually for each protein to match the corresponding experimental values (see Tables 1 and 2). Masses and charges of the amino acids can be found in Table S1.

Table 1:

List of proteins used for force field parameterization.

Protein	Sequence length	Ionic Strength (mM)	$R_g^{\text{exp}}\left(\text{nm}\right)$a	Experimental Method
CspTm83	67	42	1.37 (0.07)	FRET
IN83	60	50	2.25 (0.11)	FRET
ProTα-N83	112	42	2.87 (0.14)	FRET
ProTα-C83	129	42	3.70 (0.19)	FRET
R1563	114	128	1.72 (0.09)	FRET
R1763	100	128	2.29 (0.11)	FRET
hCyp63	167	85	2.00 (0.10)	FRET
Protein-L84	64	128	1.65 (0.10)	FRET
ACTR85	71	199	2.51 (0.13)	SAXS
hNHElcdt85	131	199	3.63 (0.18)	SAXS
sNase86	136	117	2.12 (0.10)	SAXS
α-synuclein87	140	156	3.3 (0.3)	FRET

^aValues in parentheses correspond to standard deviations.

Table 2:

List of proteins used for testing force field transferability.

Protein	Sequence length	Ionic Strength (mM)	$R_g^{\text{exp}}\left(\text{nm}\right)$	Experimental Method
An1688	185	0	4.44	SAXS
ERM TADn89	122	239	3.96	SAXS
Histatin-590	24	150	1.38	SAXS
Nucleoporin 15391	81	162	2.4	FRET
p5392	93	208	2.87	SAXS
SH4-UD93	85	217	2.9	SAXS

U_nb(r) describes nonbonded energies, and is the sum of the contact energies between all pairs of amino acids i and j separated at a distance r_ij, given by $U_{\text{nb}}(r)={\sum }_{ij}{V}_{nb}\left(r_{ij}\right)$. Instead of the Ashbaugh-Hatch functional,³⁰ we utilized a dampened step function with the following form

$$V_{\text{nb}}\left(r_{ij}\right)=\frac{{ϵ}_0}{r_{ij}^{12}}+{ϵ}_{IJ}^{\text{HPS}}\mathcal{C}\left(r_{ij}\right).$$ (9)

The first term with ϵ₀ = 1.67772 × 10⁷ kJ/mol Ź² accounts for excluded volume. ${ϵ}_{IJ}^{\text{HPS}}$ measures the strength of the pairwise contact energies and I and J correspond to the amino acid types of residue i and j. Parameters in $\mathcal{C}\left(r_{ij}\right)$ (Eq. 3) were chosen such that V_nb(r_ij) approximates the shape of the Lennard-Jones potential (see Figure S1). This new potential form separates out the repulsive core from specific amino acid interactions such that the model contact energies can be directly compared with the correction terms introduced in Eq. 2.

Details on computer simulations

At each iteration of the force field optimization algorithm (Figure 1), we carried out two set of replica exchange molecular dynamics simulations for each protein using U_MOFF(r) and U_ME(r), respectively. The amino acid contact energies in U_MOFF(r) were set as zero in the first iteration. We note that, except for the first iteration, U_ME(r) is defined differently from Eq. 1 and refers to the energy function that corrects the current version of MOFF, and

$$U_{\text{ME}}(r)=U_{\text{MOFF}}(r)+\alpha R_g(r).$$ (10)

The biasing strength α was fine tuned manually for each protein to ensure that the average R_g for simulated protein structures is within 0.5 Å of the experimental value.

All simulations were carried out using the GROMACS software package,⁶⁰ with the PLUMED plugin to incorporate biasing energies.⁶¹ Simulations were initialized from protein structures predicted by I-TASSER⁶² using the corresponding amino acid sequences. Each simulation trajectory consists of a total of six replicas with temperatures at 300K, 320K, 340K, 360K, 380K, and 400K, and swaps between replicas were attempted at every 100 steps. Langevin dynamics were used to control the temperature with a coupling constant of 1 ps. Proteins were placed inside cubic boxes with sides five times the maximum length of the protein. The trajectories lasted for 4 × 10⁷ steps with a timestep of 10 fs. The first 10⁷ steps were discarded as equilibration. We collected protein configurations at every 2000 steps for a total of 15,000 structures. Combining the two trajectories simulated with the two energy functions results in a total of 30,000 structures for each protein. To validate the convergence of our simulations, we repeated the simulations with U_MOFF(r) five times in the first and final iteration and did not observe statistically significant changes in the predicted R_g.

Results and Discussion

Illustration of force field parameterization with a single protein

To illustrate key concepts in the algorithm for force field optimization, we applied it to a single protein, R15. As shown in Figure 2A (blue line), U_HPS(r) overpredicts R_g with a mean of 2.23 nm compared to 1.72 nm determined by FRET.⁶³ We then carried out the maximum entropy optimization to derive U_ME(r), which succeeded in reproducing R_g as shown by the orange line. Finally, we derived a force field for this individual protein, U_R15(r), by solving Eq. 5 with 30,000 structures collected from the two simulations for U_HPS(r) and U_ME(r). As shown in green, the new force field predicts a mean R_g of 1.66 nm, which is in much better agreement with the experimental value than that predicted by U_HPS(r). Its variance also closely matches that from U_ME(r).

Figure 2:

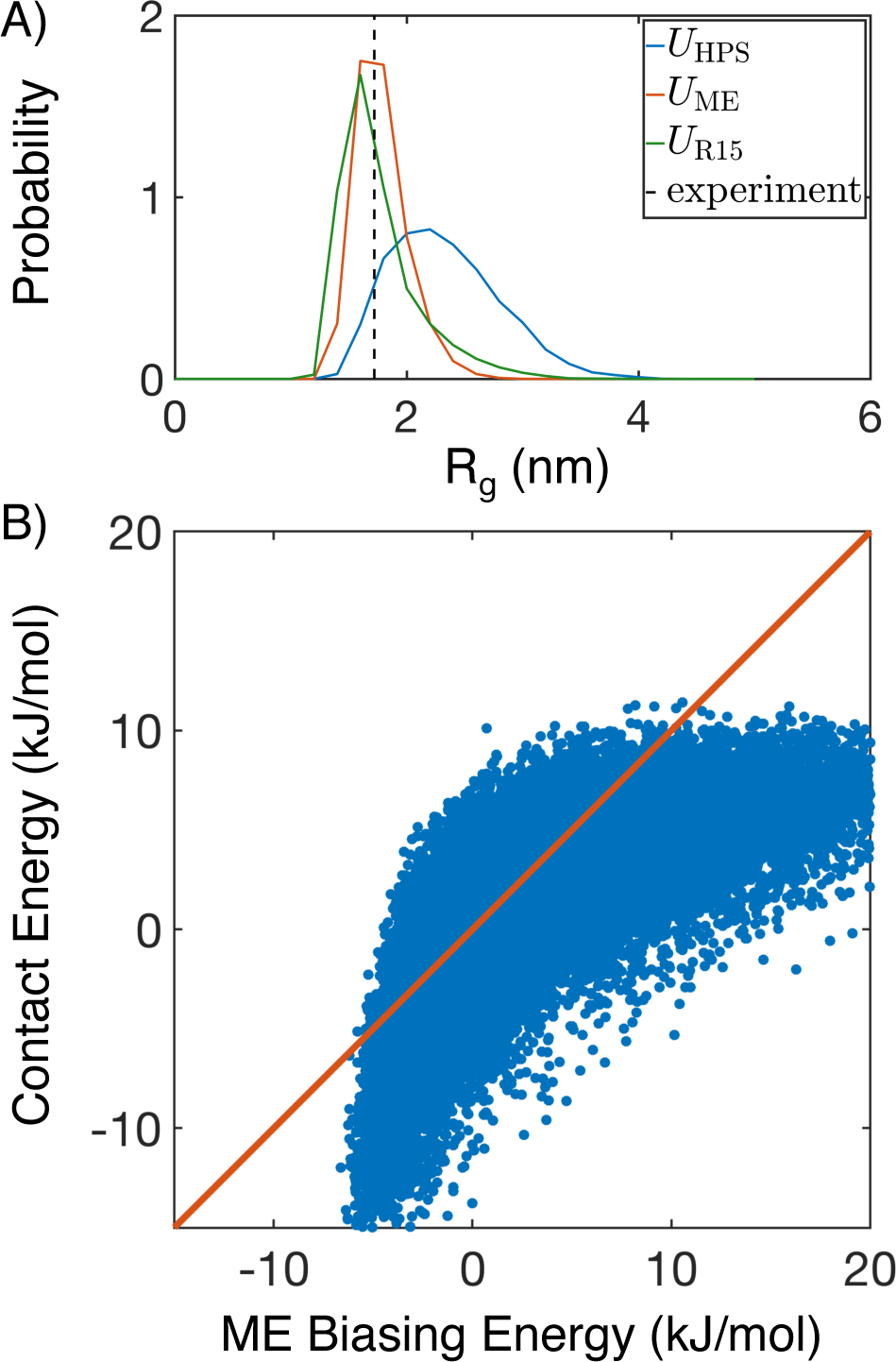
Illustration of the force field parameterization algorithm on a single protein, R15. (A) Comparison between the mean experimental value (black, dashed) for R_g and probability distributions obtained from simulating the hydrophobic scale model (U_HPS(r), blue), the maximum entropy optimized model (U_ME(r), orange), and MOFF for this specific protein (U_R15(r), green). (B) Correlation between contact energies obtained from linear fitting $\left(\sum _{I,J}{ϵ}_{IJ}\left[{\mathcal{C}}_{IJ}\left(r_m\right)-{\mathcal{C}}_{IJ}^{\text{exp}}\right]\right)$ and the original maximum entropy biasing energy $\left(\alpha \left[R_g\left(r_m\right)-R_g^{\text{exp}}\right]\right)$. The diagonal line (orange) is provided as a guide to the eye.

We then examined the accuracy of the linear approximation used in Eq. 5 by plotting the contact energies ${\sum }_{I,J}{ϵ}_{IJ}\left[{\mathcal{C}}_{IJ}\left(r_m\right)-{\mathcal{C}}_{IJ}^{\text{exp}}\right]$ against the bias energies $\alpha \left[R_g\left(r_m\right)-R_g^{\text{exp}}\right]$ for all the 30,000 structures in Figure 2B. Though the two energies are correlated, it is evident that the linear fit is not perfect, supporting the use of an iterative algorithm for further improvement. The observed oblong shape results from different physical limits on protein size and contacts. For example, fully collapsed structures have a well defined R_g value that further gives rise to a lower bound on the biasing energy (−6 kJ/mol). On the other hand, physical contacts between residues can vary substantially without changing protein size, leading to large variations in contact energies. Similarly, for expanded configurations, the contacts will disappear first before proteins become fully stretched to reach a maximum in R_g, resulting in the heterogeneity in biasing energies at a relatively constant contact energy of 10 kJ/mol.

We further applied U_R15(r) to other proteins as a test of its transferability. As shown in Figure S2, it performs worse than U_HPS(r) and tends to overcollapse the proteins. This is not too surprising as the interaction energies determined for a single protein are not guaranteed to provide a good description of IDPs in general.

Parameterization and validation of MOFF for IDPs

To parameterize a transferable force field capable of modeling IDP structures, we carried out the iterative optimization algorithm over a total of twelve disordered proteins studied in Ref. 30 (Table 1). As a quantitative evaluation of the force field performance, we define

$${\chi }^2=\sum _i{\left(\frac{R_{g,i}^{\text{sim}}-R_{g,i}^{\text{exp}}}{{\sigma }_i}\right)}^2$$ (11)

to measure the differences between simulated and experimental R_g. σ_i is the experimental standard deviation of R_g for protein i, and the sum is taken over all proteins from the training set.

A total of 15 iterations was performed to determine the final set of parameters for MOFF. As the iterations progress, χ² declined rapidly, starting at 23.67 and reaching 3.50 by the end (Figure 3A). R_g values predicted by the converged MOFF are shown in Figure 3B, along with the results from U_HPS(r). The significant improvement of MOFF over the hydrophobic scale model is encouraging and supports the usefulness of our iterative algorithm in developing more accurate protein force fields. Next, we evaluated the performance of MOFF on six additional proteins not included in our training set to test its transferability. These proteins were studied by Thirumalai and coworkers with a different model (Table 2).³⁴

Figure 3:

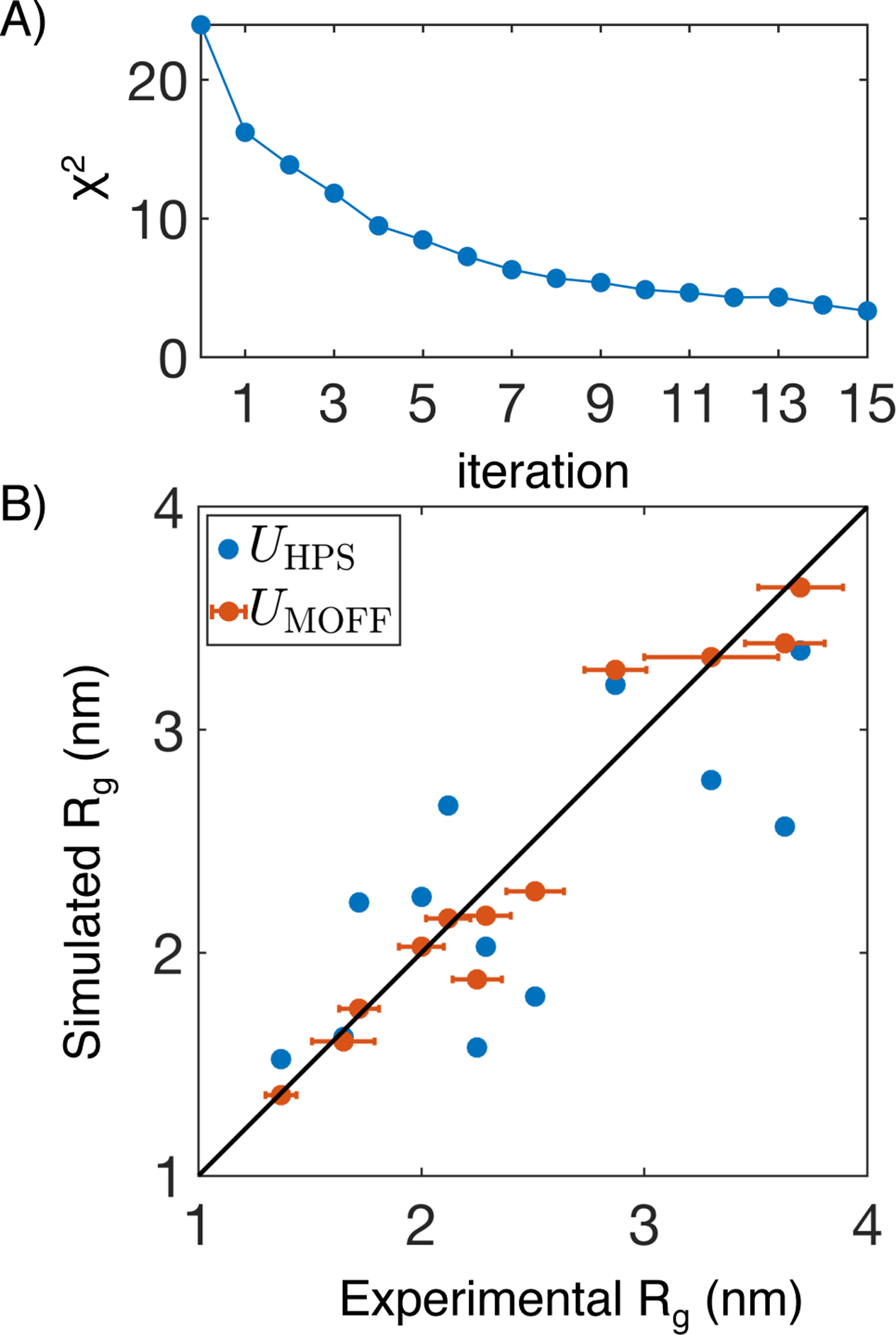
MOFF improves the prediction of R_g for proteins includes in the training set. (A) χ² that measures the normalized difference between simulated and experimental R_g values as a function of the number of iterations for force field optimization. (B) Comparison between experimental R_g and those predicted by the hydrophobic scale model (U_HPS(r), blue) and MOFF (U_MOFF(r), orange). Error bars represent experimental standard deviations. Simulation errors are comparable to the symbol size.

As shown in Figure 4, MOFF significantly improves the prediction accuracy for these new proteins as well. The total sum of absolute difference $\sum _i\left|R_g^{\text{sim}}-R_g^{\text{exp}}\right|$ drops from 5.51 to 2.30 nm when compared with predictions by the hydrophobic scale model. The monotonic decrease of this difference along MOFF optimization (see Figure S3) supports the absence of overfitting for force field parameterization. It’s worth noting that the improvement exhibits heterogeneity and the result on ERM TADn is the least satisfying, as highlighted by the arrow in Figure 4. Analysis of the underlying protein sequence shows that ERM TADn lacks polar, uncharged amino acids that are prevalent in most IDPs (Figure S4A). These amino acids constitute a much higher fraction of the training set and more successful portions of the test set. Similarly, large, apolar amino acids are less frequent in the training set than in ERM TADn. The increased levels of hydrophobic residues coupled with the decreased levels of hydrophilic ones likely explains the more collapsed configuration of ERM TADn. Therefore, MOFF is transferable, but performance can potentially be further improved with a larger training set.

Figure 4:

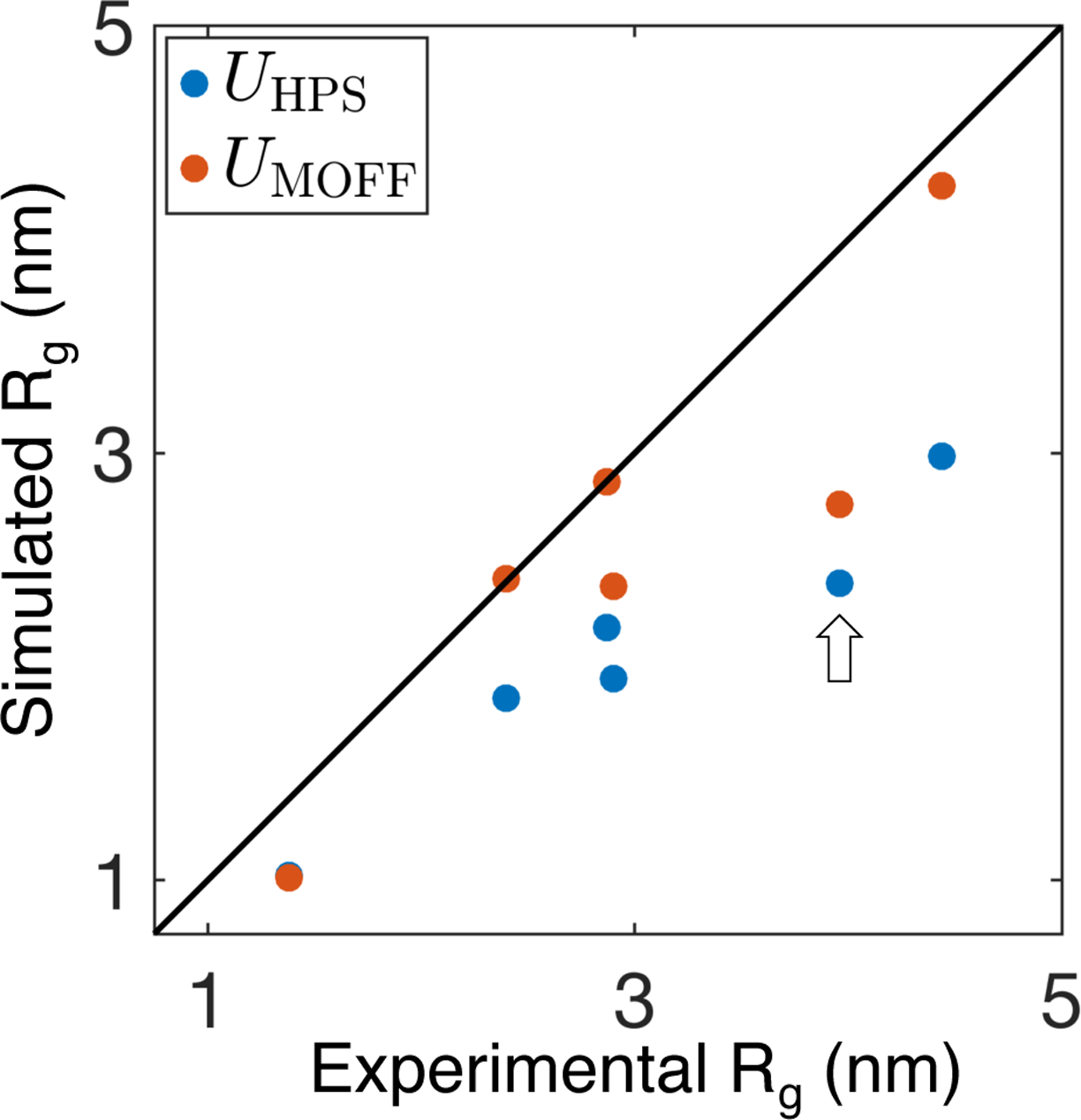
MOFF (orange) significantly improves over the hydrophobic scale model (blue) in predicting R_g for a test set of proteins not included in force field parameterization. The arrow highlights ERM TADn, which is discussed in the main text as a case where the improvement is less pronounced. Simulation errors are comparable to the symbol size.

Classification of amino acids based on MOFF interactions

Given the success of MOFF in predicting the size of IDPs, we wondered whether the derived interaction energies $\left({ϵ}_{IJ}+{ϵ}_{IJ}^{\text{HPS}}\right)$ could provide physical insight into protein folding. When compared with the hydrophobic scale model, we found that MOFF significantly increases the contact energy between hydrophilic residues (Figure 5 and Figure S5), and even makes some of these interactions purely repulsive. A more repulsive force field is necessary to rescue the overcollapse of protein configurations observed in the hydrophobic scale model. As hydrophilic residues are over-represented in IDPs and our training set (Figure S4B),^64–66 destabilizing the contacts among them is effective at expanding the configurations for most proteins.

Figure 5:

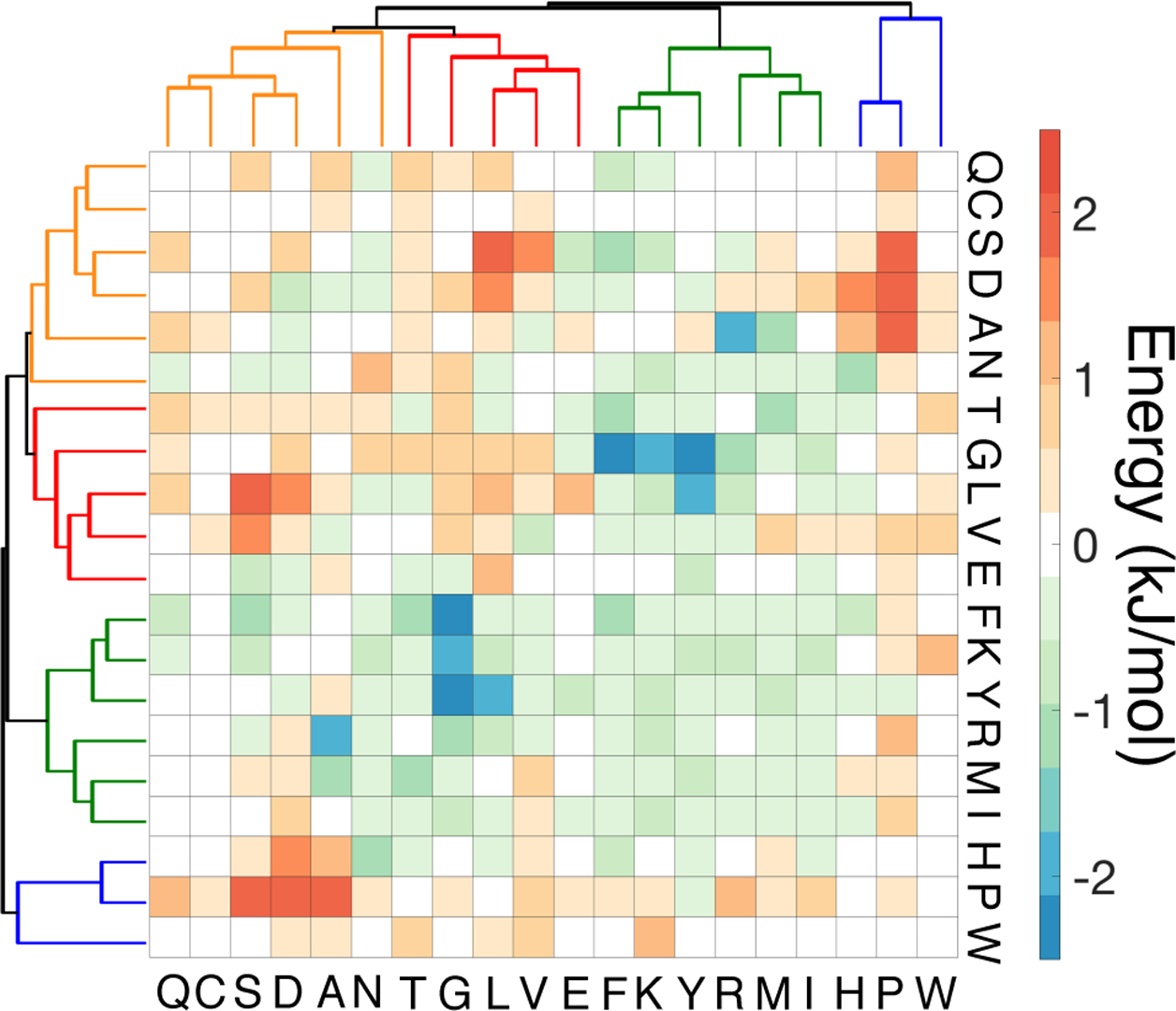
Hierarchical clustering of MOFF contact energies reveals the presence of four amino acid groups. The contact energies correspond to the sum of ϵ_IJ and ${ϵ}_{IJ}^{\text{HPS}}$ defined in Eqs. 2 and 9 respectively. The energies between residues are shown from red (most repulsive) to blue (most attractive). The four groups are displayed as orange (GLN, CYS, SER, ASP, ALA, ASN), red (GLU, THR, GLY, LEU, VAL), green (PHE, LYS, TYR, ARG, MET, ILE), and blue (HIS, PRO, TRP), respectively.

To further untangle the complexity of the MOFF interaction matrix, we performed a hierarchical clustering to group together amino acids that share similar interaction patterns. Towards that end, we assigned each amino acid with a 20-element vector that represents its interaction energy with other residues. Distances between amino acids were then defined using the correlation coefficients of corresponding vectors. After computing the proximity between amino acids, we grouped them into four clusters using the linkage function implemented in MATLAB.⁶⁷ As shown in Figure 5, hydrophilic and hydrophobic residues are generally separated from each other, partitioned into cluster 1–4 (orange and blue) and cluster 2–3 (red and green), respectively. We note that these four clusters differ from the amino acid groups derived from the analysis of the Miyazwa-Jernigan (MJ) potential that has been widely used for studying folded proteins.^68–70 As shown in Table 3, MJ groups clearly separate amino acids based on hydrophobicity, but the charged residues (GLU, ARG, and LYS) are assigned into the two primarily hydrophobic clusters 2–3 by MOFF. A possible explanation for the more scattered distribution of residues in MOFF clusters is that IDPs lack a well-defined hydrophobic core and adopt more extended conformations than well-folded proteins. The hydrophobic effect “learned” from IDP sequences, therefore, may be less prominent.

Table 3:

The five groups of amino acids derived from the Miyazwa-Jernigan potential.⁷⁰

Group	Amino Acids
Group 1	CYS MET PHE ILE LEU VAL TRP TYR
Group 2	ALA THR HIS
Group 3	GLY PRO
Group 4	ASP GLU
Group 5	SER ASN GLN ARG LYS

Next, we investigated whether this difference in amino acid clustering reflects a robust feature of IDPs or a result of statistical noise in parameterization. Towards that end, we introduced two new force fields denoted as U_MOFF4(r) and U_MJ5(r), respectively. These two force fields share the same mathematical expression as in Eq. 2, and they only differ in the amino acid clusters used in defining the second correction term. For U_MOFF4, we partitioned the 20 amino acids into the four MOFF clusters shown in Figure 5 and restricted corrections in contact energies (ϵ_IJ) to be identical for amino acids within the same cluster. Similarly, for U_MJ5, amino acids that fall into the same MJ group share the same force field corrections. We then followed the iterative procedure as before to derive force field parameters from the twelve training proteins. If the difference between the two amino acid groups is not significant but an artifact of the current optimization algorithm, we shall anticipate comparable performance from the two simplified models in simulating IDPs.

Remarkably, we found that U_MOFF4(r) essentially reproduces the success of the full model, despite its use of a much smaller number of parameters (10 compared to 210). As shown in Figures 6A and S6, U_MOFF4(r) describes the size of training proteins well, and the normalized difference between simulated and experimental R_g (χ²) decreases to 7.12 after 15 iterations. Furthermore, this new force field appears to be more transferable than our original one, and the absolute R_g difference for test proteins is 2.03 nm, smaller than 2.30 from U_MOFF(r) (Figure 6B). On the other hand, U_MJ5(r) performs significantly worse for both training and test proteins. The χ² plateaus around 15.64 after 15 iterations (Figures 6C and S6), and the R_g difference for test proteins is 4.03 nm (Figure 6D). Close examination of the simulated results for training proteins suggests that this force field loses the specificity required to adjust the size of individual proteins. Instead, it generally increases the size of each protein, regardless of how the initial force field performs.

Figure 6:

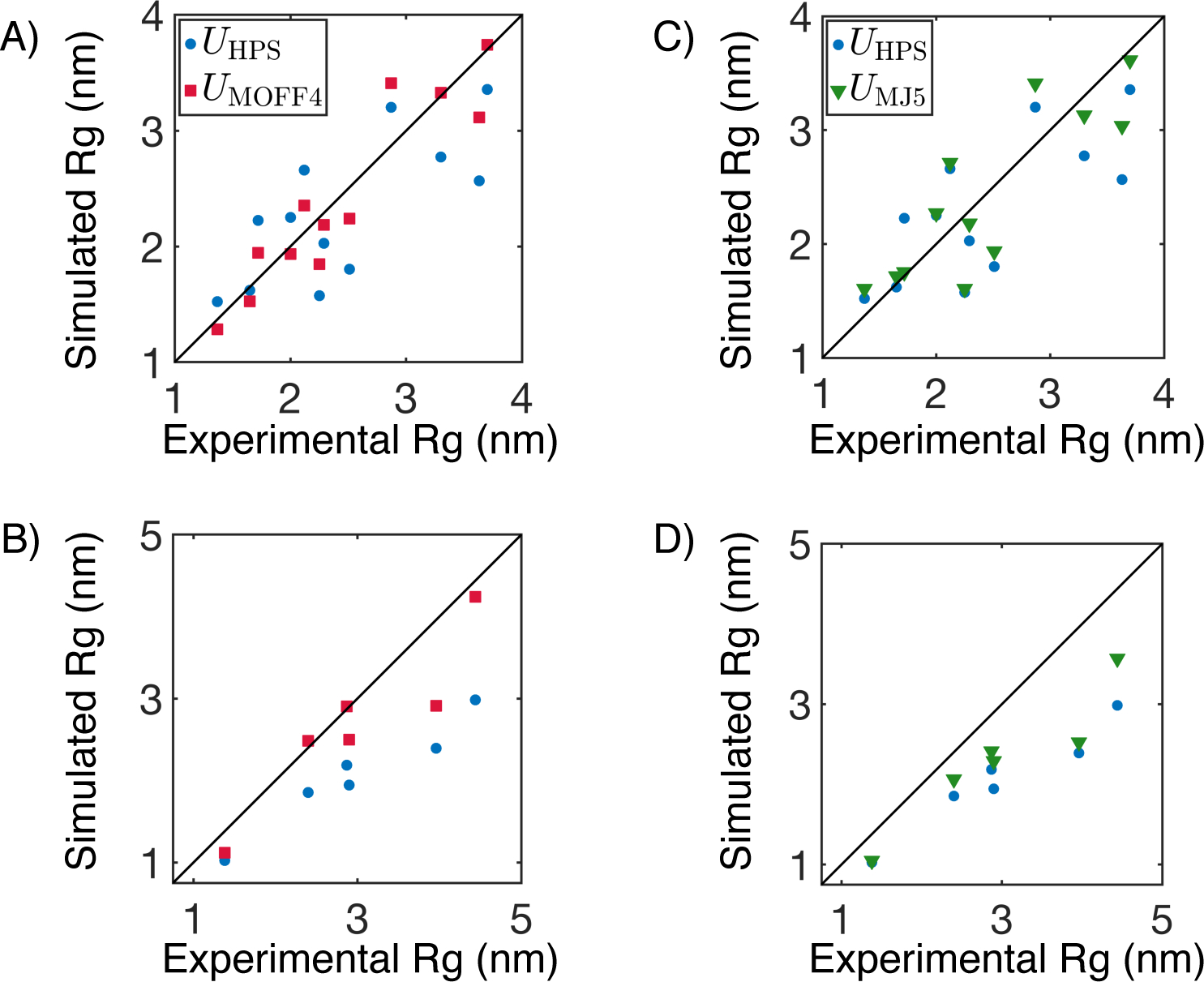
Comparison between the performance of two reduced models parameterized using amino acid clusters defined by MOFF (U_MOFF4) or MJ potential (U_MJ5). Simulated R_g on training and test proteins using U_MOFF4 are compared with experimental values in parts A and B, respectively. The corresponding results for U_MJ5 are shown in C and D. We also presented results from U_HPS in blue for reference. Simulation errors are comparable to the symbol size.

The vast difference in the performance of the two simplified models strongly supports the biological importance of the four groups defined by the MOFF energies. It also highlights the challenge for transferring models that work well with folded proteins to IDPs. We note that the presence of two different amino acid clustering schemes does not necessarily suggest the existence of two separate folding codes for disordered and globular proteins. Instead, it may indicate that the protein sequences used in parameterization are not broad enough to cover the whole spectrum of biological diversity. As the size of a protein is dictated by the subtle balance of several factors, including hydrophobic effect, water-mediated interactions, etc., a limited coverage of the sequence space may result in over- or under-emphasis of one mechanism versus the other. Optimizing parameters using both disordered and ordered sequences will be crucial to ensure the consistency and transferability of computational models across protein families.

Conclusions

We presented an algorithm for parameterizing the force field of coarse-grained models. It is most effective at refining existing force fields while other top-down^71,72 and bottom-up^73,74 approaches are potentially more appropriate for deriving new force fields from the scratch.

Our algorithm improves force field quality by introducing additional correction terms to reproduce experimental data. It, therefore, differs from many approaches that directly adjust force field parameters.^75,76 In particular, existing approaches often involve iterations of molecular dynamics simulations to compute ensemble averages and parameter fine tuning to improve the agreement between model and experiment. Modern force fields for protein molecules, especially those with atomistic details,^26–28 often involve more than hundreds of parameters. Fine tuning them is, therefore, a challenging numerical problem in a high-dimensional space, and many iterations will be needed to reach convergence. Our algorithm breaks this difficult parameter search problem into two steps consisting of maximum entropy optimization and least squares regression. Instead of directly adjusting parameters of the original force field, we introduce correction terms that can be defined independently from these parameters, effectively reducing the complexity of the optimization. For example, parameters in the maximum entropy optimization step share the same number as experimental constraints, which is often much smaller than those involved in defining the force field, and can be determined very efficiently. The second step does not involve molecular dynamics simulations and can be solved with negligible computational cost. In its current version, we used linear regression to fit maximum entropy biases for its simplicity of implementation. Non-linear fitting, however, can be adopted straightforwardly to improve the accuracy of the second step. A more accurate regression can potentially abolish the need of iteration used in the current algorithm, further reducing its computational cost.

We applied the algorithm to parameterize an IDP model using the radius of gyration for a set of proteins. The resulting force field, which we term as MOFF, succeeded in de novo structural prediction for disordered proteins. Further analysis of interaction energies from MOFF suggested a classification of amino acids that differs significantly from the five types defined by the MJ potential, a model that has found great success for studying folded proteins. We demonstrated that this difference is not a result of statistical noise in parameters and is critical for the success of MOFF in modeling IDPs. Given its accuracy and efficiency, we anticipate MOFF to be useful for elucidating sequence-specific features of IDPs that drive their phase separation and improving our understanding of the emerging disorder-function paradigm.

We note that the quality of the force field introduced here can be continuously improved. For example, due to the limited availability of experimental data, the number of proteins included in the training and test set is small. Increasing the size of the training set will, in general, lead to better force field accuracy and transferability. Furthermore, though we mainly used the radius of gyration derived from SAXS and FRET as constraints, the general framework for maximum entropy biasing makes the incorporation of data from other types of experiments such as nuclear magnetic resonance straightforward. Finally, experimental data are noisy and their interpretation is not always straightforward. Using more rigorous protocols to process experimental measurements^77–79 and accounting for errors in these data with a Bayesian optimization approach^80–82 are important future directions to further improve force field quality.

It is worth pointing out that while we restricted the discussion to disordered proteins, one can incorporate well-folded proteins into the training set for parameter optimization as well. Deriving a consistent force field for both disordered and globular proteins has been challenging. A simultaneous optimization for both folded and disordered proteins using the algorithm outlined here would be an exciting future direction. It may shed light on general principles of protein folding by resolving the difference in amino acid clustering derived from MOFF and MJ potential.