Absolute and Relative Knowledge of Ordinal Position on Implied Lists

Abstract

Does serial learning result in specific associations between pairs of items, or does it result in a cognitive map based on relations of all items? In 2 experiments, we trained human participants to learn various lists of photographic images. We then tested the participants on new lists of photographic images. These new lists were constructed by selecting only 1 image from each list learned during training. In Experiment 1, participants were trained to choose the earlier (experimenter defined) item when presented with adjacent pairs of items on each of 5 different 5-item lists. Participants were then tested on derived lists, in which each item retained its original ordinal position, even though each of the presented pairs was novel. Participants performed above chance on all of the derived lists. In Experiment 2, a different group of participants received the same training as those of Experiment 1, but the ordinal positions of items were systematically changed on each derived list. The response accuracy for Experiment 2 varied inversely with the degree to which an item’s original ordinal position was changed. These results can be explained by a model in which participants learned to make both positional inferences about the absolute rank of each stimulus, and transitive inferences about the relative ranks of pairs of stimuli. These inferences enhanced response accuracy when ordinal position was maintained, but not when it was changed. Our results demonstrate quantitatively that, in addition to item-item associations that participants acquire while learning a list of arbitrary items, they form a cognitive map that represents both experienced and inferred relationships.

“Serial learning” refers to the ability to learn an ordered list, and the relations between list items. Whether the information about serial order is an explicit, or implicit feature of the task, humans and animals are able to learn such lists. During explicit training of seral learning, subjects are required to respond to all of the items in the correct order, for example, A-B-C-D-E, to earn a reward. During implicit training of serial learning, subjects are presented only with pairs of items, and are required to respond to the first item in order to earn a reward. For example, if all the items in the correct order are ABCDE, then on AB trials, rewards are provided for responding to Item A; while on BC trials, rewards are provided for responding to Item B, and so forth.

In studies of transitive inference (TI), subjects are asked to choose between pairs of items, and rewarded for choosing whichever item comes first in a sequence of items previously ordered by the experimenter. Subjects are not informed anything about the task demands, and are never shown all of the items. Nevertheless, subjects learn to respond as though they have learned the relations between all of the items. When subjects are only trained on adjacent pairs of items (e.g., AB, BC, CD, and DE), they respond correctly to the earlier list item when provided subsequent novel pairings (e.g., BD). This suggests that experience with adjacent pairs of items of a list is sufficient to infer the relations among all possible item pairings of the same list. Such performance has been reported in a wide range of species (Jensen, 2017). Thus, adjacent pair training provides the bare minimum of information for which an entire ordering of items of a list can be derived.

The primary purpose of this study is to determine whether participants can acquire sufficient knowledge of an item’s ordinal position to support comparisons of items taken from separate training lists. It is known, for example, that, following training on adjacent pairs from two ordered lists (ABCDE and VWXYZ), one can respond correctly to the presented pairs BD and WY. What we do not know is how accurately they would respond to pairs BY or WD or, more generally, to pairs composed of items from which no two items came from the same training list.

We incorporated the method of “derived lists” (Chen, Swartz, & Terrace, 1997; Ebenholtz, 1972). Following training on items from five different training lists, five “derived lists” were created by selecting one item from each of the training lists. Therefore, all of the items in a derived list were equally familiar to the participants. However, the presentations of each pair of items for the derived lists were novel, because no two items in a derived list were from the same training list. The critical question was whether participants could consistently select the item with a lower rank.

Proposed Models of TI

Explanations of how subjects learn a TI task are varied. One possibility is that subjects form multiple pairwise associations between stimuli and their corresponding rates of reward (reviewed in Vasconcelos, 2008). Under such models, the only way to evaluate a novel pairing is to compare the experienced rates of reward for each item. This approach uses differential reward rates as a signal of list position. It can therefore make inferences about stimuli with differential rates of reward (such as always favoring the first item in a list, because it is rewarded 100% of the time it was selected in the past). However, for pairs that do not have differential reward rates (e.g., the pair BD, for which each stimulus has a 50% chance of earning a reward following training), the best the model can do is guess (Jensen, Muñoz, Alkan, Ferrera, & Terrace, 2015). Such models are also vulnerable to manipulations that manipulate experienced reward rate separately from the list ordering. Framed in terms of the model-based versus model-free dichotomy used in reinforcement learning and behavioral neuroscience (reviewed in Maia, 2009), one can say that recent experimental evidence does not favor a model-free approach to explaining TI (e.g., Lazareva & Wasserman, 2012) because merely keeping track of the expected value of each alternative without using a representative model does not explain the observed patterns of behavior.

Another view is that subjects form a representation of the items in sequence, in which each stimulus has a “position” relative to other stimuli (Terrace, 2012). According to this model-based view, feedback is not only used as a signal of expected reward, but also as evidence for updating a model of stimulus position. Because comparisons of position along a continuum are necessarily transitive, this model predicts robust TI in a wide variety of settings, including those that manipulate rate of reward independently of stimulus position. Experimental results confirm that TI is resilient to such manipulations. This has been presented as evidence that a representation of stimulus position gives a more comprehensive account of TI performance than model-free learning (Jensen, Alkan, Ferrera, & Terrace, 2019). Support for this view has also been reported in comparative neuroscience (e.g., Brunamonti et al., 2016).

Other mechanisms for making relative judgments have also been proposed. Ranking of stimuli and related phenomena could arise from propositional coding (Banks & Flora, 1977) or from the linguistic application of formal logic (Clark, 1969). The difficulty in evaluating these models is that, in general, they do not make clear predictions about specific paradigms. That makes it difficult to evaluate whether a given result is consist with such a theory (Gazes, Chee, & Hampton, 2012). Also, an extensive literature on TI in animals (reviewed by Jensen, 2017) showed that neither linguistic aptitude nor formal logic is needed. Indeed, complex cognitive processes such as these can, in some cases, be computationally implemented without recourse to semantic coding, such as “naming” items or reasoning about their positions using propositional logic (Cueva & Wei, 2018; Kumaran, 2012). At the same time, much of this literature, especially experiments in which subjects are only trained on adjacent pairs, cannot explain performance by associative or reward-expectation models, because there are many circumstances in which the models predict chance performance, but human and animal performance exceeds chance. As new computational models proliferate, it is important to probe the contents of cognitive representations to determine which models resemble actual behavior and which do not.

Some models of serial learning, particularly those developed to explain performance under the immediate serial recall (ISR) task (e.g., Henson, 1999), emphasize the relative character of serial inferences, relating the location of each stimulus to some landmark. Because the ISR task has a temporal structure with a clear start and end to the list, it makes sense to ask whether performance can be explained as a function of time since the start (primacy) or time prior to the end (recency). Under this approach, the first and list items can be seen as temporal “landmarks” against which other list positions might be judged. However, this approach does not translate well to TI tasks. A well-controlled TI task randomizes the order in which stimuli are presented, and all stimuli are presented many times during training. Because each stimulus appears at a uniform rate throughout training, no stimulus displays temporal primacy, or recency, over any other stimulus. Under TI tasks, time cannot be the basis for labeling certain stimuli as landmarks, or for judging a distance between stimuli. By contrast, a representation of stimulus position is akin to a spatial map than a temporal duration, which would treat each stimulus as its own landmark relative to other elements in the list. This approach provides a good account of TI performance in monkeys and humans (Jensen et al., 2015).

What remains unclear is whether the relative positions of stimuli in one list translate in any way to other lists. Consider again a case in which a participant has learned that A > B > C > D > E and V > W > X > Y > Z, and are then queried about the relationship between B and Y. The position of “A” in a representation of ABCDE may make it preferable to B, but there is no logical relation between A and Y. Relative position within a list provides no indication that B > Y, unless the additional assumption is made that the position of A is comparable to that of V. If participants routinely select B over Y, we can conclude that a heuristic based strictly on within-list landmarks cannot be responsible for their performance. In order for landmarks to generalize (i.e., a landmark for “start of the list”), it is necessary to make the assumption that stimuli with a rank of 1 in two different lists are somehow comparable.

Relative Versus Absolute Comparisons

The absolute minimal representational framework that supports TI is one based on relative position or value. Given only that A > B and B > C, one may infer using transitivity that A > C but no further inferences about the values of A, B, and C are possible. Under Stevens’ (1946) system of classification, such comparisons require only an ordinal measurement scale. Introducing the comparison that D > E provides no clues about how either D or E relate to A, B, and C. In this respect, TI can be accomplished on the basis of relative comparisons of stimuli alone. In order to explain the manner in which participants respond to new combinations of stimuli, these relative comparisons (i.e., comparisons using only an ordinal scale of measurement) are not sufficient.

We propose a form of inference that we call positional inference, in order to explain performance given knowledge of orders of items across different lists (derived or otherwise). Positional inference incorporates the additional assumption that knowledge of an item’s position within one list generalizes to knowledge of the same item’s position within other derived lists (e.g., Merritt & Terrace, 2011). This corresponds to the assumption that the rank of a stimulus is represented in absolute terms, using an interval scale of measurement, and not simply relative to the other training stimuli. It follows that the degree to which performance is improved or degraded for pairs in derived lists depends on whether an item’s ordinal position is maintained or changed, and that this can be used to infer the content of serial knowledge. If subjects routinely make positional inferences, their performance will provide clues about the representations that encode the positions of each list item and the ability to compare those positions. Computationally, this could be implemented using a cognitive map, in which the processes that underpin the judgments are spatial (Abrahamse, van Dijck, Majerus, & Fias, 2014; Jensen et al., 2015). Use of such cognitive maps has been associated with activity in the hippocampus and the ventral medial prefrontal cortex (Tse et al., 2011).

If TI training results in knowledge of relative position, items that are further apart in a list should be easier to discriminate. That hypothesis is supported by a symbolic distance effect (SDE), whereby response accuracy increases as a function of the distance between items (D’Amato & Colombo, 1990; Moyer & Landauer, 1967). Although semantic models have sought in the past to explain symbolic distance effects (e.g., Banks & Flora, 1977), spatial models not only predict SDEs, but also predict the relative size of those effects. If stimuli are represented within a cognitive map at roughly even intervals and with some location uncertainty, then the probability of an error should shrink by a relevant unit measure as the distance between stimuli grows (and thus the overlap between the two estimates of position shrinks). When studies have examined performance among novel pairs, spatial models of item position consistently predict error rates (Jensen, Altschul, Danly, & Terrace, 2013; Jensen et al., 2015).

We will use “absolute” serial knowledge to refer to an encoding framework in which the positions of stimuli in many different training lists share the same underlying continuum that can be described using an interval scale. In the list ABCDE, the stimulus C has a position that corresponds to the third rank, independent of the positions of other stimuli. Similarly, in the list FGHIJ, the stimulus G has a position that corresponds to the second rank. If participants are rewarded for choosing the item of lower rank, than on the basis of position alone (i.e., by way of a positional inference), participants should infer that G > C, even if they have not previously seen G and C paired with one another. By contrast, we define “relative” serial knowledge to consist of comparisons that are based on the transitive property of serial ordering: that a participant who has learned that B > C and C > D should infer that B > D because ordinal rank is transitive.

Absolute and relative knowledge can both contribute to accurate performance on a novel trial. Given the above lists, if training consisted only of adjacent pairs from each of the training lists, then the inference that G > D involves both a positional inference based on absolute knowledge (that G has a rank of 2 and D has a rank of 4) and a transitive inference based on relational knowledge (that Rank 2 > Rank 4, even though those ranks were not directly compared during training).

In Experiment 1, we trained human participants to learn the order of a list of photographic stimuli by presenting adjacent pairs of items drawn from five different five-item training lists. Participants were then tested on all pairs (both adjacent and nonadjacent) of items from five different five-item derived lists. In these derived lists, each item was selected from a different training list, with the constraint that the ordinal positions of all items on the derived lists were maintained. Thus, for Experiment 1, the positions of items that were learned during training sessions retained their ordinal positions during testing sessions (A from List 1 is still the correct response when paired with B from List 3, etc.). The manipulation in Experiment 1 is not a change in the list orderings (as the absolute position of each stimulus remains unchanged), but of the list elements. Thus, each derived list consists of items that were never been directly compared during training. Because the pairs presented at test were all novel, knowledge of their ordinal position during training was the only basis for responding correctly to such pairs during test. Participants’ performance allowed us to map the contents of the resulting serial representation.

In Experiment 2, the ordinal positions of items during training and testing differed to varying degrees. A different group of participants were trained on adjacent pairs of items drawn from the same five 5-item lists as used in Experiment 1. However, participants were tested on lists in which the ordering of items was systematically changed. Reliance on positional inference should result in decreased accuracy as a function of the degree to which the ordinal positions were systematically changed. For example, accuracy should be higher in response to pairs drawn from the derived list A₂B₅C₄D₁E₃ than the accuracy to pairs drawn from the derived list B₃C₁D₂A₄E₅, because the former retains the ordering learned during training, while the latter disrupts that ordering somewhat (each list is identified by a numerical subscript). Furthermore, performance for the list B₃C₁D₂A₄E₅ should in turn be better than performance for the list A₁E₄C₅D₃B₂, because the former ordering has more pairs in common with the training order than the latter ordering.

Experiment 1: Derived Lists With Maintained Ordinal Positions

Our first experiment builds systematically on the findings of two earlier studies that investigated knowledge of relative position (Chen et al., 1997; Merritt & Terrace, 2011). The aim was to determine if participants could transfer their knowledge of an item’s ordinal position to derived lists when the original ordinal item positions were maintained.

Method

Participants.

Participants were 35 college undergraduates (21 female, 14 male) who earned course credit. The experiment was approved by Columbia University’s Institutional Review Board (protocol AAAA7861), conforming to the guidelines for human research set forth by the American Psychological Association.

Apparatus.

Participants performed the experiment on a personal computer (a factory-standard iMac MB953LL/A with 8Gb of RAM), with responses made via a mouse-and-cursor interface. The task was programmed in JavaScript (making use of the Node and Express modules) and run in the Google Chrome web browser, set to full-screen mode. The relevant task code is included in the online supplemental materials.

Procedure.

All participants first completed a training procedure, which introduced them to five lists, each composed of five different items (photographic images). Hereafter, we will denote the list position using a letter. For example, ABCDE is a five-item list, where each letter denotes a different item. The identity of the list from which it was drawn is indicated with a numerical subscript. For example, the items in the first list were A₁B₁C₁D₁E₁, where A₁ denotes this list’s first item and E₁ denotes its last item. Similarly, B₄ denotes the second item in the fourth list (see Figure 1). Importantly, list order does not refer to the temporal order in which stimuli are presented. Stimulus A has a lower ordinal rank but, as described below, that is not relevant to whether it is the first stimulus that participants see.

Figure 1.

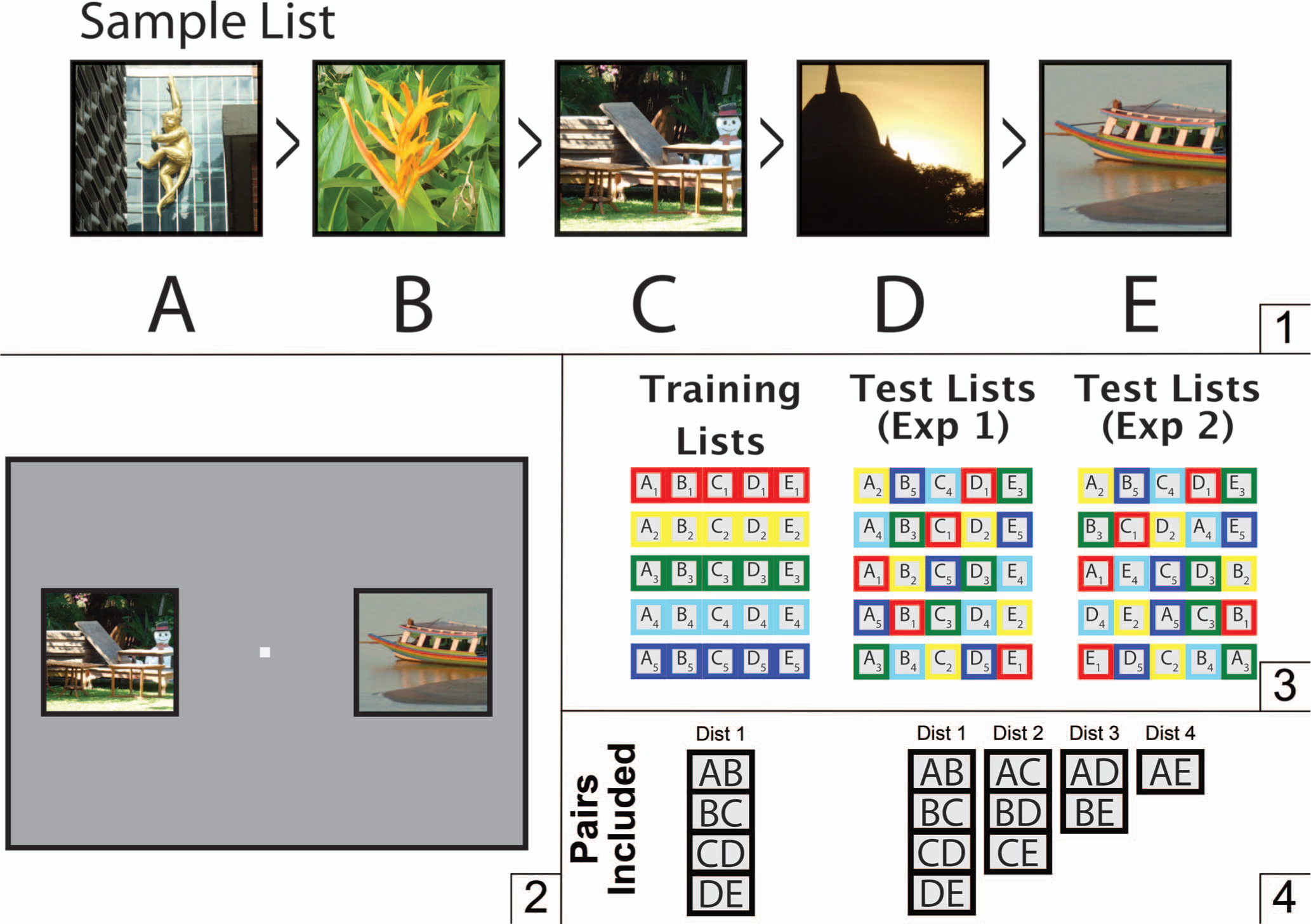
Procedure for TI with derived lists. (1) Example of a five-item list. The images used in each list were chosen at random from a large database of stock photos, and followed no organizational schemes. (2) Example of what is seen by participants. Only two stimuli were ever visible at a time on the monitor. In this case, the pair CE is being presented. (3) During training, participants were presented only with pairs of items that were adjacent to each other in a list. During testing, new lists were derived by “recombining” the pairs of items to be presented such that each testing list consisted of pairings of items that were novel to the participant. (4) Examples of the symbolic distance effect (SDE). Items with a symbolic distance of 1 (Dist 1) are the items that are adjacent to each other in a list, while the larger the spatial distance of the items in a list, the larger the SDE (Dist 2–4). See the online article for the color version of this figure.

Participants did not know the name of the study at the outset or its purpose. It was simply designated by an experimental number (“Experiment 1”). Each participant was given the following verbal instructions: “Use the mouse to click on images. Each response is either correct or incorrect. Correct responses are indicated by a green check mark appearing on the screen, whereas incorrect responses are indicated by the appearance of a red cross. Try to make as many correct responses as possible.” Participants were assured, via their consent form, that the experiment was not expected to pose any physical or emotional risks. No further information was provided about the nature of the study until data collection was complete, and the instructions gave no indication was provided that the images had any kind of ordering until participants were debriefed.

All tasks were structured such that each configuration of a pair of items was presented once, before that configuration was presented a second time. For example, if only the adjacent pairs of items in list ABCDE were presented, then a “set” of trials would consist of one presentation each of AB, BA, BC, CB, CD, DC, DE, and ED, in a randomized order. Randomization and counterbalancing were important to prevent participants from responding to patterns of when and where stimuli were presented, that is, to prevent participants from exploiting spatial and temporal cues. Such patterns could potentially undermine the objective of training the implied list order.

These steps ensured that pairs of items were presented in a uniform fashion throughout each session, such that the nth presentation of each stimulus arrangement appeared before the (n + 1)th presentation of any pairing appeared. Feedback at the end of each trial was the only information that could be used to infer list order.

During each trial, participants were presented with one pair of adjacent stimuli. They had to select one stimulus to proceed to the next trial. There was no time limit. Selecting the item with an earlier list position was always the correct option, while selecting the other item was always incorrect. Thus, given the pair B₁C₁, selecting B₁ would be correct and selecting C₁ would be incorrect. Because the images were arbitrary, subjects had to infer both the task requirements and the list order by trial and error. Throughout the experiment, trials advanced at a consistent rate, and aside from the presentation of stimuli, no further cues (e.g., an extra delay) signaled when participants began a new phase of training. No verbal instructions aside from those already described above were given. Participants did not interact with the experimenter again until the end of the experiment.

Training consisted of 10 blocks of 32 trials (and thus 320 trials total) on each of the following lists:

• List 1:

  A₁B₁C₁D₁E₁

• List 2:

  A₂B₂C₂D₂E₂

• List 3:

  A₃B₃C₃D₃E₃

• List 4:

  A₄B₄C₄D₄E₄

• List 5:

  A₅B₅C₅D₅E₅

During the first block, participants were only presented with adjacent pairs from the first list (A₁B₁, B₁C₁, C₁D₁, and D₁E₁). The presentation of each pair of images was counterbalanced (e.g., A₁ was equally likely to appear on the left of the screen vs. on the right) to avoid spatial confounds. Thus, counting the counterbalanced pairings, each stimulus pairing was shown eight times during Block 1.

Blocks 2 through 5 proceeded in an identical fashion, using stimuli from Lists 2 through 5. Finally, during Blocks 6 through 10, participants were reexposed to the five training lists, this time beginning with List 5, then List 4, and so on, such that List 1 was retrained in Block 10. Hereafter, Blocks 1 through 5 will be collectively referred to as “first training,” because they made use of photographic stimuli that were novel at the outset of each block. By contrast, Blocks 6 through 10 were composed of the same photographic stimuli as those of initial training. These blocks will hereafter be referred to as “second training,” because the participants were presumed to be familiar with the stimuli throughout this phase.

Testing of derived lists began at the end of second training (that is, on Trial 321). Participants were not provided any signal or cue to indicate that training had ended and testing had begun. During testing, participants were presented with five derived lists, which were composed by selecting one item from each of the training lists. In each instance, the ordinal position of the item that was selected was maintained (cf. Figure 1).

• List 6:

  A₂B₅C₄D₁E₃

• List 7:

  A₄B₃C₁D₂E₅

• List 8:

  A₁B₂C₅D₃E₄

• List 9:

  A₅B₁C₃D₄E₂

• List 10:

  A₃B₄C₂D₅E₁

During each testing block, all 10 possible stimulus pairs, composed of both adjacent and nonadjacent pairs of items, were presented. All of these pairs of items were derived from Lists 1–5, as denoted by the item subscripts. Thus, during Block 1 of testing, participants were presented with the pairs A₂B₅, A₂C₄, A₂D₁, A₂E₃, B₅C₄, B₅D₁, B₅E₃, C₄D₁, C₄E₃, and D₁E₃. As during training, the presentations of these pairs were counterbalanced for stimulus position, and correct responses were indicated by the appearance of a green check mark. Incorrect responses were indicated by the appearance of a red cross. Each pair was presented four times during each block. Each of these derived lists used one stimulus from each of the training lists, ensuring that all 10 stimulus pairings for each derived list was novel at the start of Experiment 1. Each testing block was 40 trials long. Accordingly, the testing phase of Experiment 1 consisted of 200 trials.

Analysis.

To characterize performance during training, we fit a multilevel logistic regression. Parameters were fit using the Stan language (Carpenter et al., 2017), which allowed us to obtain posterior distributions for our model parameters using a variety of Hamiltonian Monte Carlo sampler called the No-⋃-Turn Sampler (Hoffman & Gelman, 2014). This approach offers clear advantages over other popular MCMC samplers (such as BUGS and JAGS), particularly when the posterior distribution has both high dimensionality and nontrivial covariance. The details of our analysis, including the script that implemented the model, are provided in the online supplemental materials. This approach allowed us to fit models describing population parameters and to obtain estimates and corresponding uncertainties for individual participant parameters.

During training, the probability of a correct response for each participant was governed by the logistic function:

$$p(\mathit{\text{Correct}})={\left(1+\text{exp}\left(-\left({\beta }_{\varnothing }+{\widehat{a}}_t\cdot t\right)\right)\right)}^{-1}$$ (1)

Here, β_Ø is an intercept that represents performance at “trial zero” (t = 0) whereas β_t is a slope term that represents the learning rate over successive trials, t. Parameters for first training and second training were estimated independently. All participants’ parameter values of β_Ø and β_t were presumed to be drawn from a population distribution that was simultaneously estimated. Because Experiments 1 and 2 both used the same training procedure, data from the training sessions of both experiments were pooled to obtain better overall estimates.

The symbolic distance effect (SDE) of serial learning suggests that response accuracy increases as a function of the spatial distance between items. Because symbolic distance was potentially a covariate of interest, a more complicated logistic model was used, following the logic of Jensen, Altschul, Danly, and Terrace (2013) and fit using the Stan language:

$$p(\mathit{\text{Correct}})={\left(1+\text{exp}\left(-\left({\beta }_{\varnothing }+{\beta }_t\cdot t+{\beta }_D\cdot D+{\beta }_{Dt}\cdot D\cdot t\right)\right)\right)}^{-1}$$ (2)

Here, D denotes the “centered” symbolic distance between stimulus pairs. Because the smallest symbolic distance is one and the largest is four, each pair was assigned a value of its symbolic distance, minus 2.5. Thus, although the symbolic distance of A₂B₅ was one, it was encoded as a value of D=1.5 in the model, whereas A₂E₃ was encoded as a value of D = 1.5. This ensured that both β_D (the contribution of symbolic distance to the intercept) and β_Dt (the contribution of the symbolic distance to the slope) as uncorrelated as possible with the overall parameters for the slope and intercept. Equation 2 was only used to model the test data, since the training phase had no variation in symbolic distance.

Results

Participants learned all of the training lists and responded accurately on all of the derived lists (Figures 2 and 3). In addition, a symbolic distance effect was immediately evident during testing (Figures 3 and 4).

Figure 2.

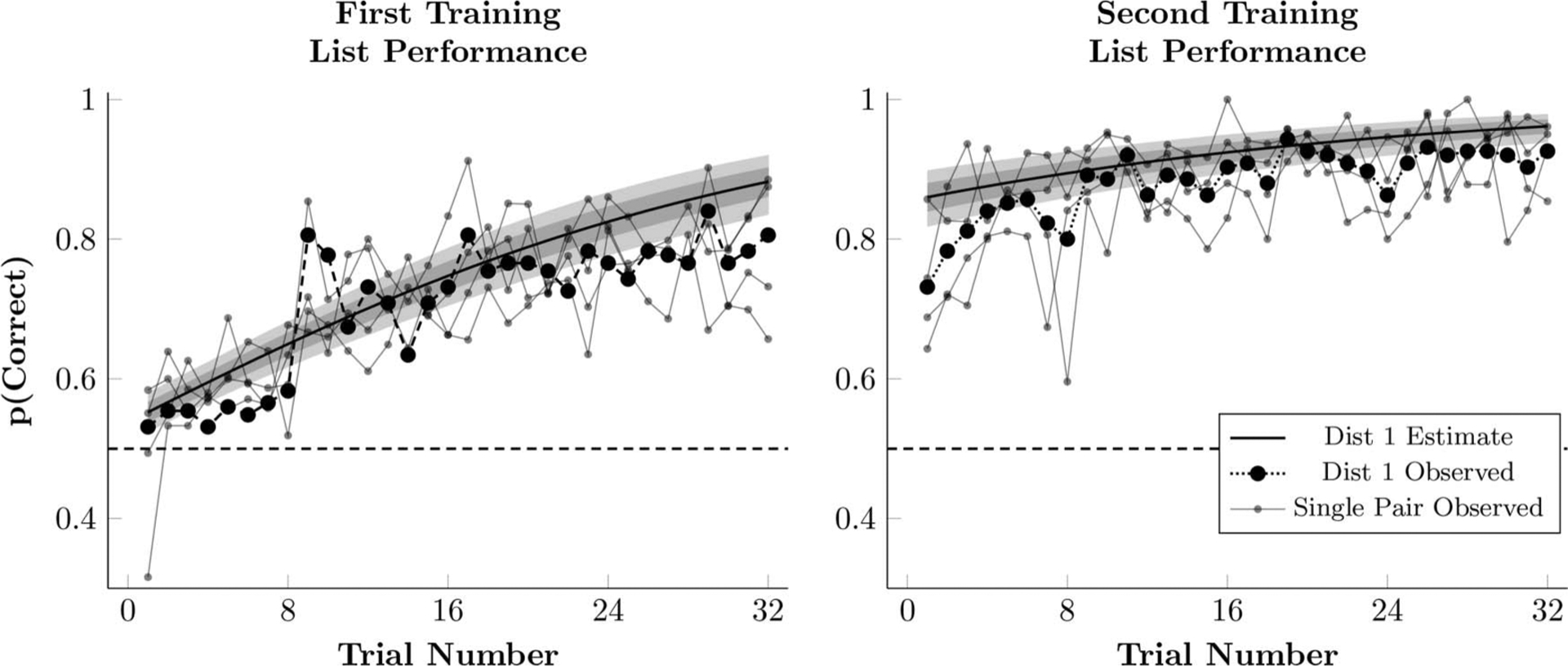
Observed proportion of correct responses during first and second training in Experiment 1 (black points), as well as the estimated performance of a participant whose logistic regression parameters (Equation 1) are the respective posterior population means. This estimate also includes the 80% credible interval (dark shaded region) and 99% credible interval (light shaded region) for the estimates performance. Also plotted are the empirical means for each of the four adjacent pairs, AB, BC, CD, and DE (small gray points). Estimated performance takes participants from both experiments into account, because both experienced the same training procedure.

Figure 3.

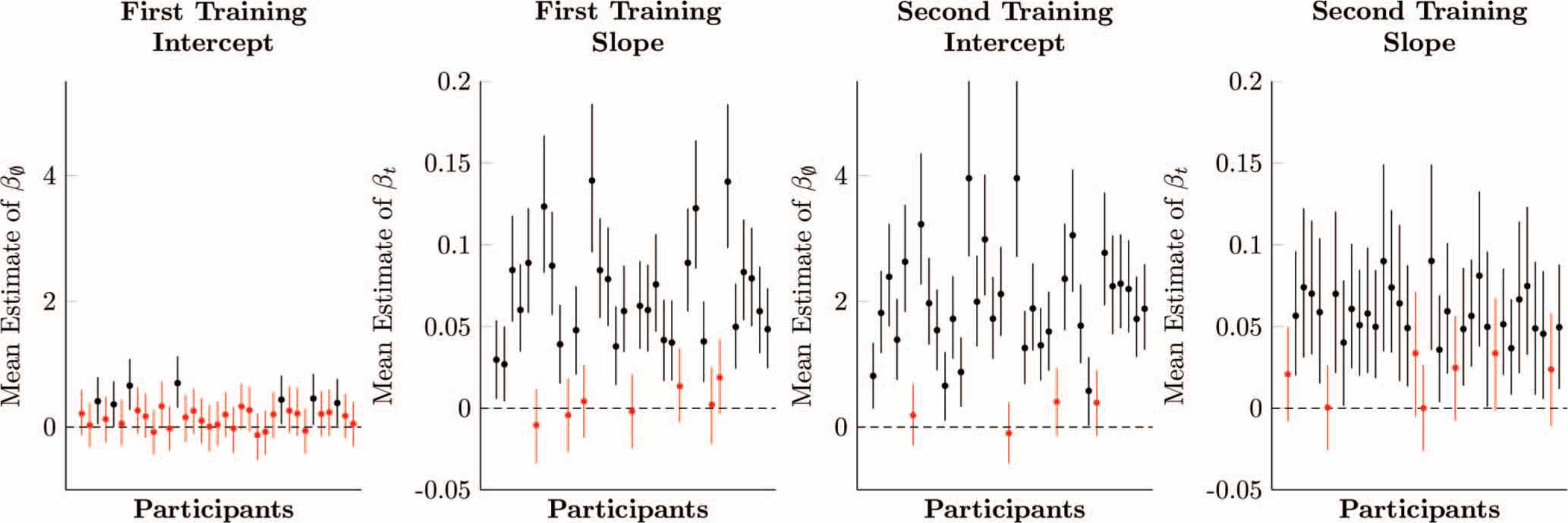
Estimates of logistic regression parameters for each participant, based on multilevel models, of first training (left column) and second training (right column) in Experiment 1. Whiskers on each estimate denote its 95% posterior credible interval. Estimates in red include zero within their credible intervals, whereas estimates in black do not. See the online article for the color version of this figure.

Figure 4.

Observed proportion of correct responses in Experiment 1, as well as the estimated performance of a participant whose logistic regression parameters (Equation 2) are the respective posterior population means. This estimate also includes the 80% credible interval (dark shaded region) and 99% credible interval (light shaded region) for the estimates performance. See the online article for the color version of this figure.

Figure 2 plots the observed proportion of correct responses, averaged across lists, along with the estimated response accuracy during the first and second training sessions of a hypothetical mean participant for each trial. Plotted are the observed frequencies (black points) and the estimated performance (solid lines) of all the participants.

Although response accuracy began at chance during first training, it increased steadily as training progressed. Also shown in Figure 2 (gray points), are accuracies for the four adjacent pairs, AB, BC, CD, and DE. These estimates are noisy (as they are based on less data) and are included to show that each of the four adjacent pairs was learned by the end of the first training block. Additionally, differences between the adjacent pairs, while detectable, were generally small (AB and DE were a bit more accurate than BC and CD overall).

Figure 2 also plots the estimated response accuracy of a hypothetical mean participant, given the model parameters in Equation 1. This estimated performance only gives an approximate sense of performance. The poor fit during the first training may reflect an increase in accuracy on Trial 9 because of a shift in the intercept. The elevated accuracy on Trial 9 does not appear to be a fluke. Based on a bootstrapped analysis, the gap between Trials 8 and 9 does not appear to be the result of the same underlying rate of correct responses (p < .0001; see the online supplemental materials for details).

Figure 3 plots the participant-level parameter estimates for the intercept (left) and slope (center left) during first training. Only seven out of 35 participants had intercepts whose 95% credible interval excluded zero, suggesting that most participants began at chance levels. However, 28 participants had slopes whose 95% credible interval excluded zero. With both parameters taken into consideration, 28 participants were responding above chance by the end of first training (based on 95% credible intervals).

Figure 3 also plots the parameter estimates for the intercept (center right) and slope (right) for participants during second training. Thirty-one out of 35 participants had intercepts whose 95% credible intervals excluded zero. Twenty-eight out of 35 participants had slopes whose credible intervals excluded zero, but some of these participants had nonzero intercepts. Taking both parameters into account, 33 participants were responding above chance by the end of second training (based on 95% credible intervals).

Figure 4 shows evidence of a symbolic distance effect immediately after training on derived lists began. The observed proportion of correct responses, averaged across lists, are shown for each symbolic distance (black = SD 1, red = SD 2, blue = SD 3, green = SD 4) during training on derived lists. These data provide evidence of both transitive and positional inferences. This is also borne out by the estimated response accuracy of a hypothetical mean participant, given the model parameters in Equation 2. On the first trial, a symbolic distance effect was evident (65% response accuracy for SD 1, 75% accuracy for SD 2, 82% accuracy for SD 3, and 88% accuracy for SD 4), despite those stimuli having never been previously paired.

Figure 5 shows parameter estimates (with 95% credible intervals) for each participant. 31 of the 35 participants had intercepts whose credible interval excluded zero, and thus performed above chance overall for the first test pair (without taking symbolic distance into consideration). Furthermore, 32 participants had a positive slope. When both parameters are taken into account, 33 participants were responding above chance overall by the 40th trial of each derived list.

Figure 5.

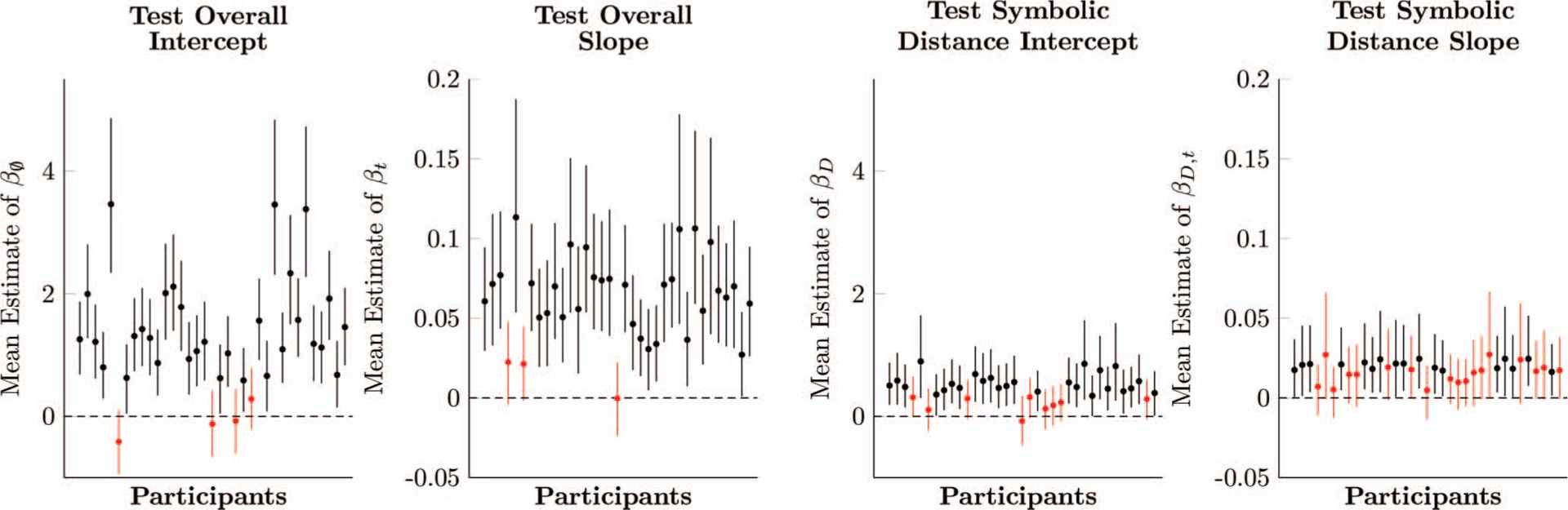
Estimates of logistic regression parameters for each participant in Experiment 1, based on multilevel models. Whiskers on each estimate denote its 95% posterior credible interval. Estimates in red include zero within their credible intervals, whereas estimates in black do not. See the online article for the color version of this figure.

Fewer participants showed a clear symbolic distance effect on the first trial. Only 26 participants had a symbolic distance intercept modifier β_D that excluded zero from its 95% credible interval, and only 17 had a slope modifier that excluded zero. When both modifiers were taken into account, the same 33 participants who responded above chance also showed a distance effect by the 40th trial of each list.

Discussion

Most participants successfully transferred their knowledge of ordinal position from training to testing on derived lists for which ordinal position was maintained. This was shown by greater than chance accuracy on the first trials of novel pairings during test and by the values of the intercept parameters β_Ø, which were consistently greater than zero.

Additionally, most participants displayed a SDE during their first exposure to all pairs, as evidenced by β_D parameters greater than zero. The symbolic distance effect is often interpreted as evidence of transitive inference, as it suggests that stimuli are arranged along a continuum (Jensen et al., 2015). With derived lists, however, it is also necessary to assume the transitive inference account is only possible if paired with an additional positional inference. Otherwise, there is no logically necessary relationship between items from different lists, say, B₁ and D₂.

Although participants’ performance reliably improved over the course of the test phase (as demonstrated by the slope parameter β_t), the results were more equivocal regarding the effect of symbolic distance on learning rate (as shown by the small values of β_Dt). Despite being small (with many participant-level credible intervals overlapping with zero), the overall trend was for participants to display slopes greater than zero. These results were obtained after only 320 trials. This suggests that, in a larger sample, there may be a differential rate of learning that depends on distance that is independent of the distance effect commonly observed on the first trial. It also seems reasonable to assume that the size of these effects would have been even more pronounced had participants received additional training.

Experiment 2: Derived Lists With Changed Ordinal Positions

The design of Experiment 2 was similar to that of Experiment 1, but in Experiment 2, the ordinal position of items was changed for four of the five derived lists. Given five 5-item lists, there are 120 possible permutations of those item positions, far too many to test exhaustively, especially within-subjects. Consequently, we selected a fixed set of representative permutations for the derived lists in Experiment 2. In one case, the order was maintained from training to test, as in Experiment 1. In another, the derived list had the ordinal positions of items entirely reversed relative to training. The remaining three lists changed the ordinal positions of items to intermediate degrees relative to training.

Method

Participants and apparatus.

Participants in Experiment 2 were 77 college undergraduates (47 female, 30 male), who used the same apparatus, received the same instructions, and were subject to the same oversight as those in Experiment 1.

Procedure.

Participants first completed the same training procedure as those in Experiment 1: Training consisted of presenting adjacent pairs of items for 10 blocks of 32 trials (and thus 320 trials total) on each of the five lists. Following this, five new lists were derived and used for testing. Participants were not provided any signal to indicate that training had ended and testing had begun. As in Experiment 1, feedback for correct and incorrect responses was provided during the training and testing sessions.

As in Experiment 1, each new list used for testing in Experiment 2 was derived by recombining items from the lists used during training. However, in Experiment 2, only one of the five derived lists maintained an item’s ordinal positions. Some of the ordinal positions were not maintained on the remaining four lists. The degree to which an item’s position was changed was specified by the number of adjacent transpositions needed to get from the original ordinal position used during training to the new ordinal position in the testing list. We refer to these changes in the absolute ordinal positions as “transposition distance,” or TD.

• List 6:

  A₂B₅C₄D₁E₃ (transposition distance = 0)

• List 7:

  B₃C₁D₂A₄E₅ (transposition distance = 3)

• List 8:

  A₁E₄C₅D₃B₂ (transposition distance = 5)

• List 9:

  D₄E₂A₅C₃B₁ (transposition distance = 7)

• List 10:

  E₁D₅C₂B₄A₃ (transposition distance = 10)

Thus, if pair E₁D₅ from List 10 was presented in this experiment, a green check appeared on the screen if the participant chose the item, E₁, because List 10 consists of a complete reversal of the order implied during training, and thus E₁ has a lower rank than D₅ in this list.

As in Experiment 1, the letter in this notation denotes the position of the stimulus during training (i.e., every “A” was in the first list position during training), whereas the numerical subscript denotes which training list the stimulus came from (e.g., A₄ refers to the first item in the fourth training list). The lists above represent the testing order of the derived lists. Thus, in List 7, four of the items (B, C, D, and A) are in different list positions at test than they were during training.

The degree to which item order in each derived list was changed can be measured by the number of adjacent item transpositions needed to get from the original ordinal order to the new ordinal order. Going from ABCDE to BACDE requires one transposition (A ↔ B). The more transpositions one needs to get from the training order to the testing order, the less the testing order is said to resemble the training order. This count of transpositions will hereafter be denoted by “transposition distance” or TD. Transposition distance has been formally studied as the “Jaro-Winkler distance” (Jaro, 1989). For example, List 7 requires at least three transpositions (A ↔ B, then A ↔ C, then A ↔ D). Thus, its TD is 3. However, to get from the training order to List 9 requires at least seven transpositions (C ↔ D, then B ↔ D, then A ↔ D, then C ↔ E, then B ↔ E, then A ↔ E, then B ↔ C), and so its TD is 7.

TD also represents the number of item pairs whose ordering was inconsistent with the order implied by the positions of the items during training. For example, List 7 has three pairs of items that are inconsistent with the orderings learned during training (BA, CA, and DA). Hence, TD = 3 for that list. The other seven pairs in List 7 were consistent with the orderings learned during training (BD, CD, etc.). List 9, however, had seven item pairs that were inconsistent with orderings learned during training (DA, DC, DB, EA, EC, EB, and CB), and so is TD = 7. List 10 represented the maximum possible transposition distance: a full reversal of the original ordering of positions of items, in which the order of all 10 pairs had was inconsistent with training.

Rather than present these lists in a fixed sequence for all participants, each participant experienced them in a randomized order. Thus, while one participant may have tested on List 6 first, another may have instead begun with List 9.

Because changes in ordinal position were expected to disrupt performance, the amount of testing time for each list was doubled. For each list, each of the 10 possible pairs of items was presented eight times (or four times per counterbalanced screen arrangement).

To avoid imposing assumptions on the parameter estimation, each of the five lists was allowed to have its own set of parameters from Equation 2. Thus, each participant had 20 parameters (β_Ø, β_t, β_D, β_Dt, all for each of five lists). These were presumed to covary at the population level, so they were simultaneously estimated. Details are provided in the online supplemental materials.

Results

Performance for the derived lists with changed ordinal positions varied inversely with the degree of transposition distance. As in Experiment 1, participants were able to learn the ordinal positions of items of all five lists presented during training (see Figure 6). The Stan language was used to fit a multilevel model to training data from participants. We also compared the performance of a hypothetical “average participant” from this model with the observed average response accuracy across Experiment 2’s 77 participants. As in Figure 2, the accuracy of the four adjacent pairs is included to show that each of these was well-learned, and that differences in performance between each of the adjacent pairs was generally small.

Figure 6.

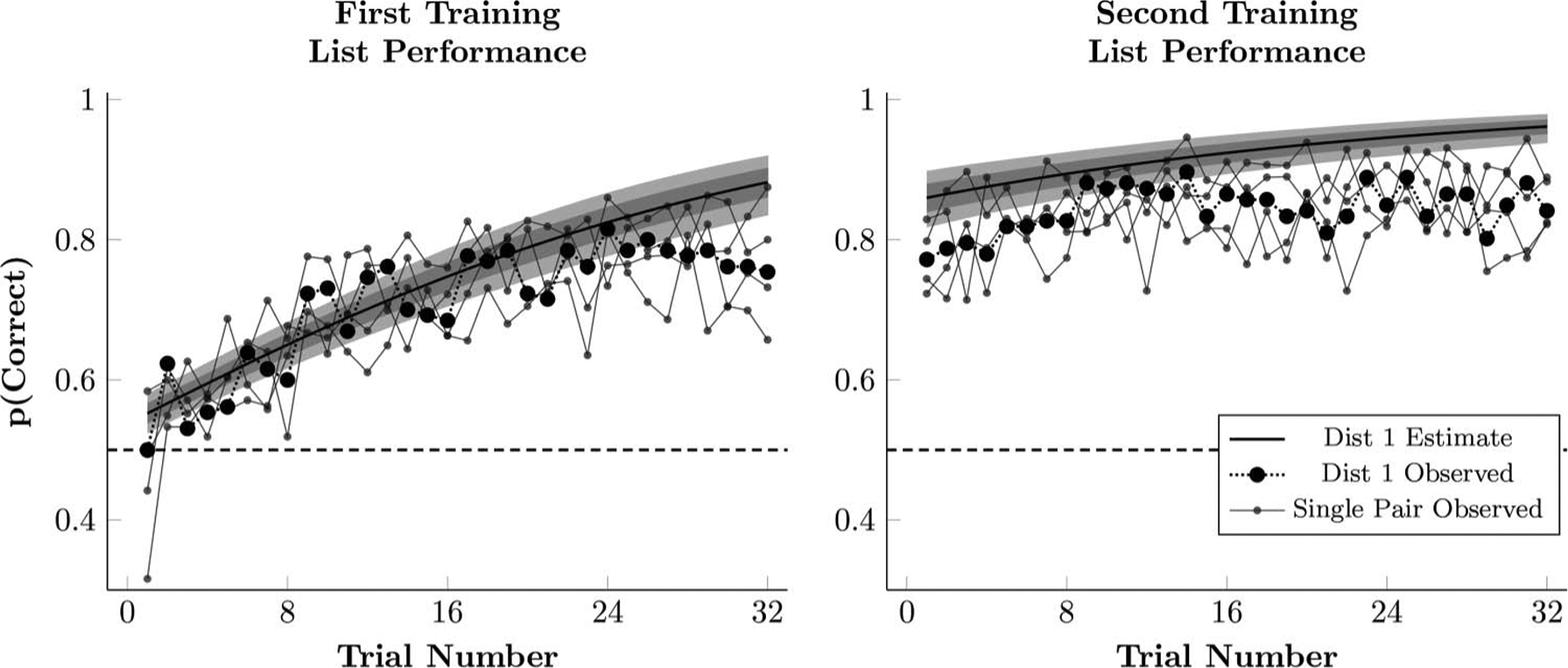
Observed proportion of correct responses during first and second training in Experiment 2 (black points), as well as the estimated performance of a participant whose logistic regression parameters (Equation 1) are the respective posterior population means. This estimate also includes the 80% credible interval (dark shaded region) and 99% credible interval (light shaded region) for the estimates performance. Also plotted are the empirical means for each of the four adjacent pairs, AB, BC, CD, and DE (small gray points).

Figure 7 shows the participant-level parameter estimates for the slope and intercept during first training. Only 18 out of 77 participants had intercepts whose 95% credible interval excluded zero, suggesting that the accuracy of most participants began at chance. Additionally, 58 participants had slopes whose 95% credible interval excluded zero. With both parameters taken into consideration, 58 participants were responding above chance by the end of first training (based on 95% credible intervals). During second training, 59 participants had intercepts whose 95% credible interval excluded zero, and 50 had slopes that excluded zero. Taking both parameters into account, 62 participants exceeded chance by the end of second training.

Figure 7.

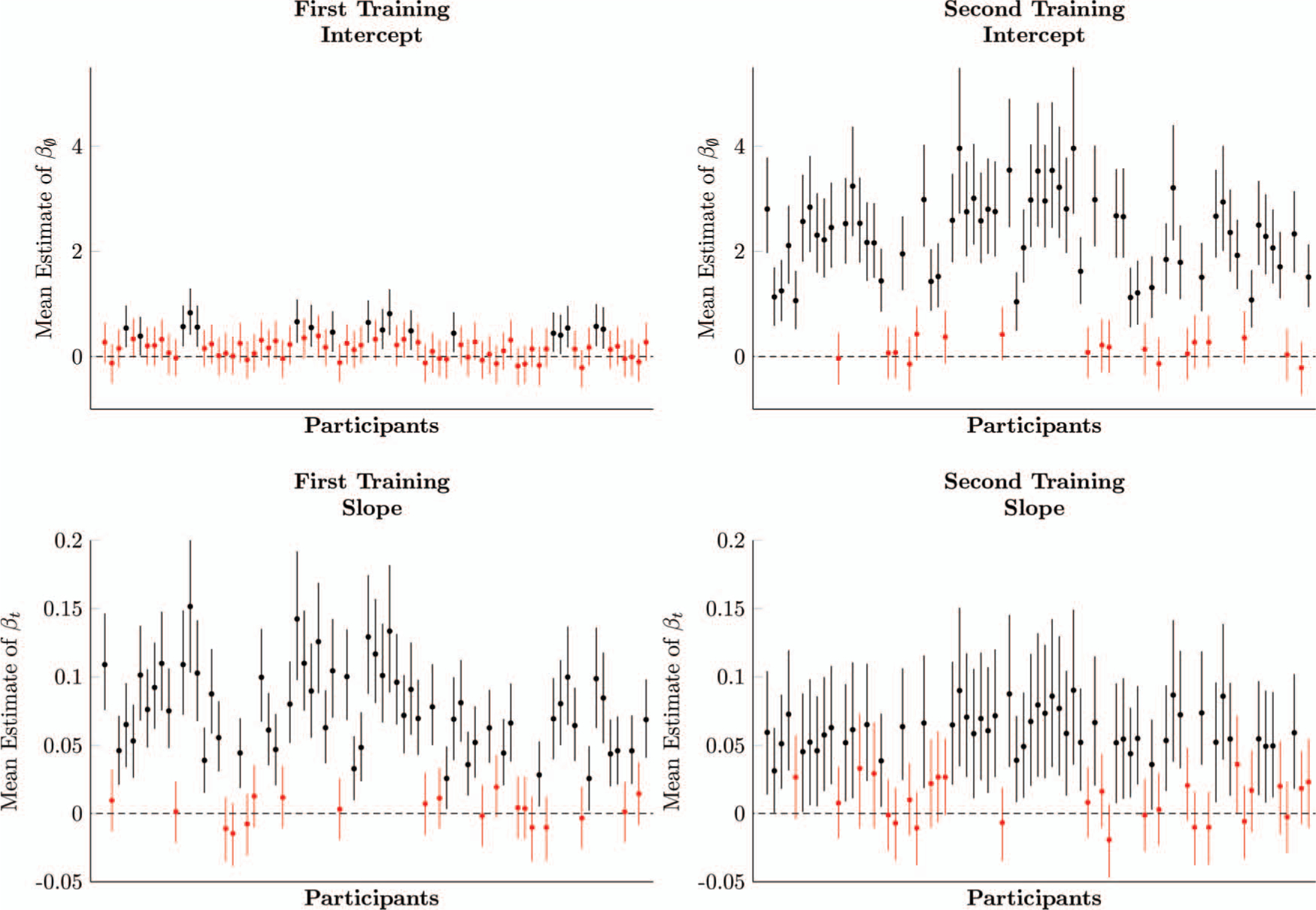
Estimates of logistic regression parameters for each participant, based on multilevel models, of first training (left column) and second training (right column) in Experiment 2. Whiskers on each estimate denote its 95% posterior credible interval. Estimates in red include zero within their credible intervals, whereas estimates in black do not. See the online article for the color version of this figure.

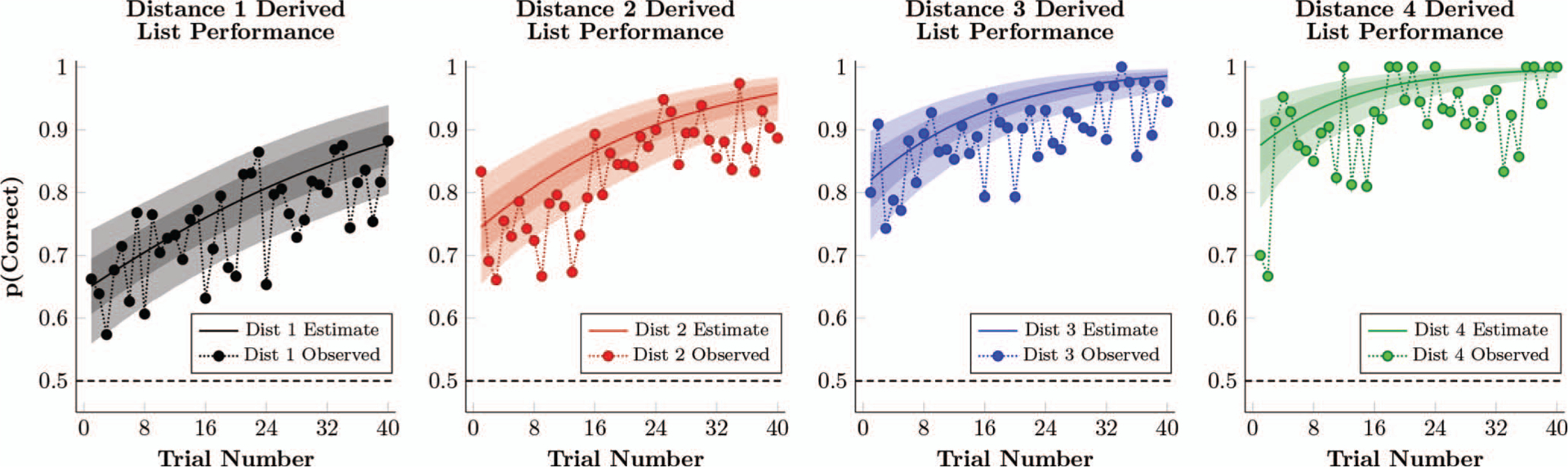
Figure 8 shows the estimated response accuracy of a hypothetical mean participant, in which the model parameters in Equation 2 were fit to each of the five derived lists. Response accuracy is clearly above chance for TD = 0, but decreases as the transposition distance increases. For TD = 10, initial performance appears to be at, or even slightly below chance, with no evidence of a symbolic distance effect.

Figure 8.

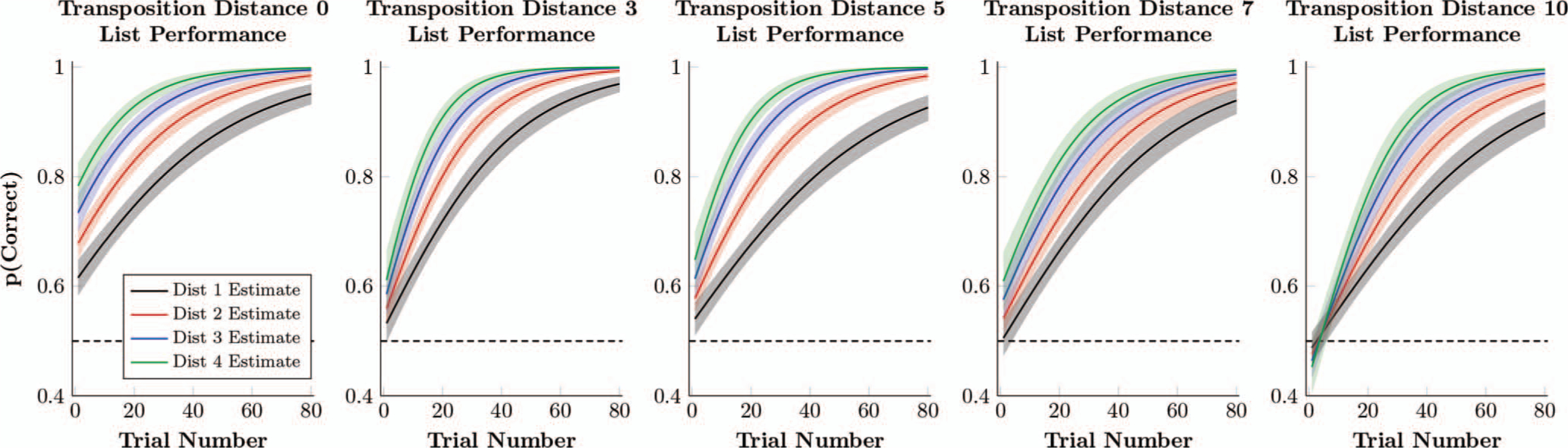
Estimated proportion of correct responses by a hypothetical participant whose logistic regression parameters (Equation 2) are the respective posterior population means. This estimate also includes the 80% credible interval (dark shaded region) and 99% credible interval (light shaded region) for the estimates performance. Performance is separated by symbolic distance (D = 1 in black, D = 2 in red, D = 3 in blue, D = 4 in green). See the online article for the color version of this figure.

Figure 9 uses violin plots (Hintze & Nelson, 1998) to depict both uncertainty about the population mean (white densities) and the joint uncertainty of the participant-level parameters (gray densities). Additionally, the means of each participant’s estimates are plotted as gray points to the right of each plot. Overall, no clear pattern emerged among the overall slopes or the slope’s interaction with symbolic distance—all participants seemed to be learning at similar rates, regardless of the ordering of the derived list. However, effects were evident in both the overall intercept parameter and in the symbolic distance parameter. The estimate of β_Ø of most participants began above chance in the TD = 0 condition but grew closer to chance as the number of transpositions increased. The symbolic distance effect on the intercept was also least ambiguous in the TD = 0 case, but was very uncertain overall and increasingly overlapped with zero for TD > 0.

Figure 9.

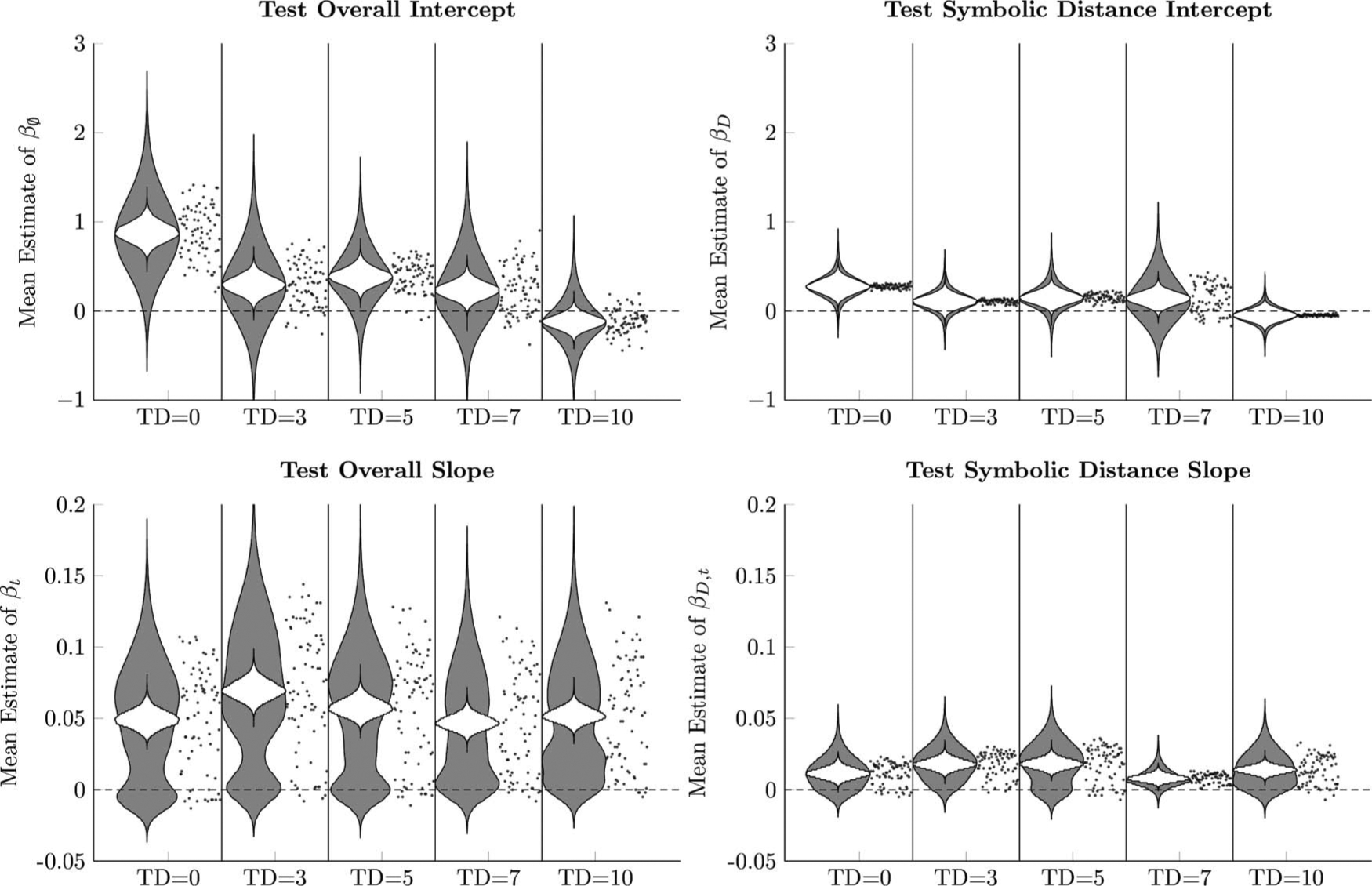
Logistic regression parameters (Equation 2) in Experiment 2 for each of the five transposition distances that participants experienced. White violin plots represent posterior distributions for the population means of logistic regression parameters (Equation 2) in Experiment 2. Gray violin plots represent the posteriors of individual means, taken jointly across all participants. Points to the right of each pair of violin plots represent the mean parameter estimates for each participant.

In Figure 9, each symbolic distance reflects both pairs that were transposed and those that were not. To identify why performance is reduced, Equation 1 was fit for every pair in every list separately, with each list receiving its own multilevel model. Figure 10 depicts the means and uncertainties for each of these posterior parameter estimates (i.e., Equation 1, as applied to each of the pairs in isolation from one another), with pairs transposed at test marked in gray. The mean parameters for each symbolic distance in the TD = 0 case provide a baseline and are denoted as a horizontal dashed line. Parameters lower than the dashed lines indicate that performance was disrupted by the transposition.

Figure 10.

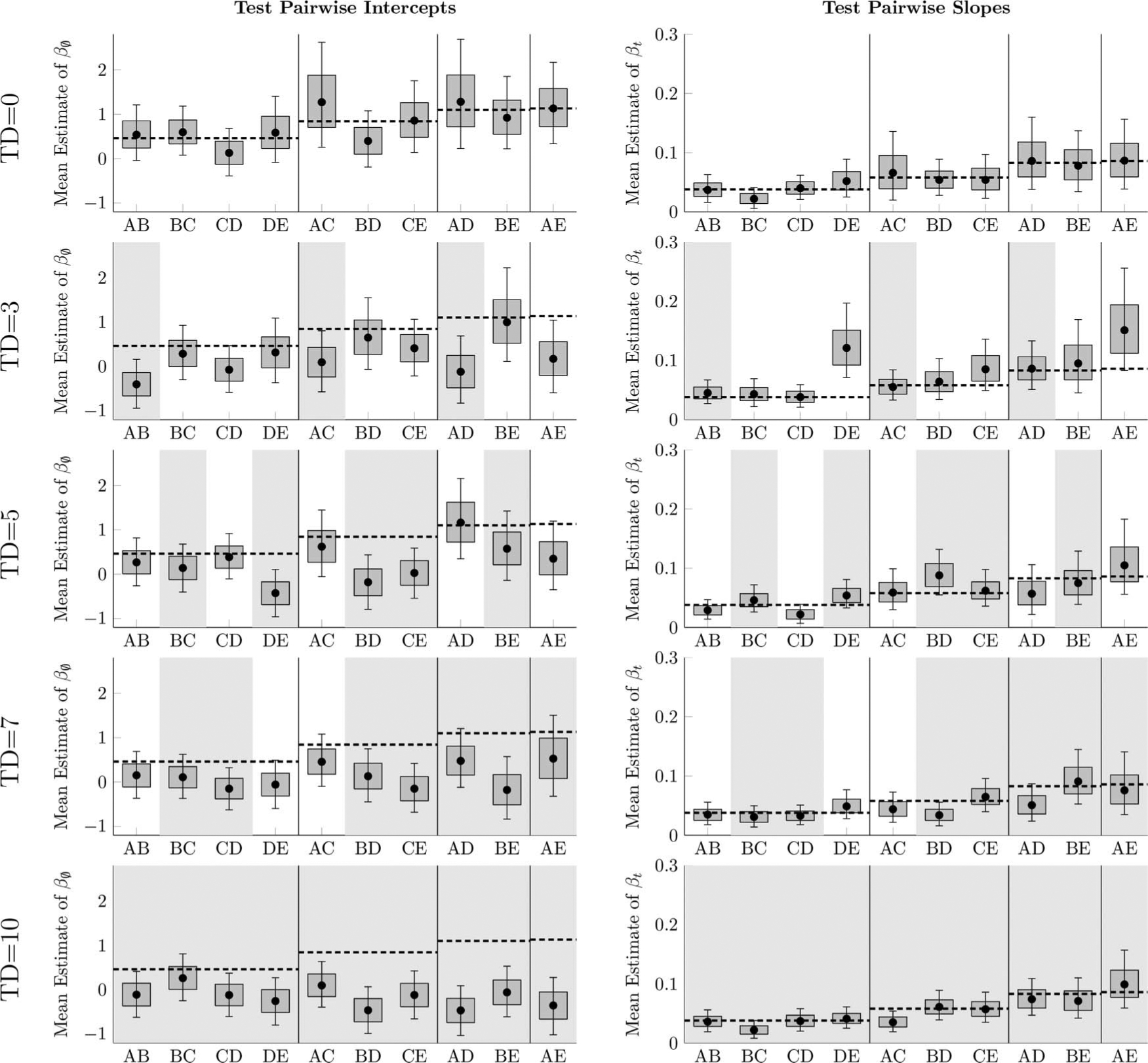
Means of logistic regression parameters (Equation 1) in Experiment 2, fit for each stimulus pairing in each transposition distance condition. Boxes represent the 80% posterior credible interval, whereas whiskers represent the 99% posterior credible interval. Stimulus pairs with a light gray background (e.g., AB for TD = 3) are pairs whose order was reversed at test from the order implied during training. Horizontal dashed lines are means for pairs of a particular symbolic distance in the condition TD = 0, to help indicate which parameters in the permuted conditions differed from the maintained condition.

Of the intercepts for the transposed pairs in the TD > 0 conditions, 80% (20/25) excluded the baseline from their 99% credible intervals, as compared with only 7% (1/15) of maintained pairs. When evaluated on the basis of the 80% credible interval, 96% (24/25) of transposed pair intercepts excluded the baseline, as compared to 46% (7/15) of maintained pairs. It therefore seems clear that initial performance was impaired by participants making positional and transitive inferences using the list orders learned in training.

By contrast, no such effects were visible among slopes. Only 16% (4/25) of slopes for transposed pairs had posterior distributions that excluded the baseline from their 99% credible interval, as compared with 6% (1/15) of maintained pairs. Based on the 80% credible interval, only 24% (6/25) of transposed pairs had posterior distributions that excluded the baseline, as compared with 40% (6/15) of maintained pairs. Thus, participants did not demonstrate an overall inability to learn the ordinal positions of items of the transposed pairs relative to those of the maintained pairs.

Discussion

As shown by the values of β_Ø in Figure 10, performance was most impaired on pairs whose orders are incongruous with those experienced during training. This is consistent with the hypothesis that participants rely on a positional inference to identify the correct response when tested with novel derived pairs.

Because every stimulus pairing is novel at test, knowledge of absolute position is needed to make correct inferences. That knowledge allows participants to infer the correct response to novel pairs. But because evidence of distance effects was also obtained from these pairs, participants also appeared to be making relative inferences. In addition, impaired performance on pairs whose ordering has changed during testing demonstrates the limitations of positional inference heuristics.

It is possible to elaborate our model by devising an omnibus model that fits data from all five phases and which uses transposition distance as a covariate. Figure 9 suggests that TD would have a roughly linear effect on the intercept terms and no effect on the slope terms in such a model. We have elected not to perform that type of analysis for two reasons. First, it is not clear that such an effect would be consistently linear. Of the 11 possible values of TD (from 0 to 10), we only tested five. It’s entirely possible that the correct pattern could be a sigmoid, or that TD = 0 and TD = 10 are “special” and intermediate values are roughly equivalent. Second, we have only tested one of a large number of possible list permutations for each TD, and it may turn out that two permutations that have identical transpositions distances (e.g., EABCD and BAEDC) would yield consistently different performance.

It is also notable that, in the complete list reversal (with a transposition distance of 10) performance is very close to chance, rather than being reliably below chance. This suggests that, although the positional inference facilitates congruous derived pairs, participants are willing to abandon their prior positional knowledge in favor of a trial and error strategy. Furthermore, once the testing phase began, the learning rate displayed for all permuted derived lists was similar. It appears, therefore, that positional inferences facilitate learning when participants are correct, but are rapidly disregarded in favor of a clean slate if they do not give rise to reliable results.

This experiment also provides a test of Henson’s (1999) proposal that using the start and end of the list as landmarks should be sufficient to support serial inference. Henson’s (1999) argument can be seen as a partial model of positional inference: one in which absolute serial knowledge is only encoded for terminal items, and other items have their positions evaluated strictly in terms of relative position. If Henson’s (1999) approach were correct, we would expect to see systematic disruption in the event that the terminal items change their position. We would also expect nonterminal items to be difficult to compare to one another without their original terminal items as points of reference. What we instead see (particularly in Figure 10) is that pairs whose ordering was unchanged tend to have accuracies that are similar to performance on a TD = 0 derived list. In other words, only the stimuli whose rank changes have their performance disrupted. This suggests to us that, in Henson’s (1999) sense, every stimulus is its own landmark (i.e., has its position represented in absolute terms). This makes serial learning uniformly robust against changes in ordering in a way that a start-and-end landmark model is not.

Transposition distance, which was an independent variable in this experiment, should not be confused with “transposition errors,” a dependent variable that is often reported in studies of short-term memory (STM; Henson, 1999). The literature on transposition errors focuses on positional knowledge in ISR tasks, which report positional learning with respect to the first and last list items as anchors, leading to higher error rates for the middle list items (Fischer-Baum & McCloskey, 2015). Significantly, those studies do not report all item-to-item relations that would facilitate inferences about novel pairs.

The similarity in positional learning in studies of working memory and our experiments should not obscure an important difference in our procedures. Serial knowledge in a TI task is only implied by feedback. The task offers no other temporal or spatial cues on which to base judgments. By contrast, ISR tasks deliberately introduce temporal cues. We consider it unlikely that the differences in performance that we report in this study depend on processes probed by ISR tasks, in which transposition errors occur in lists that are not well-learned. In TI using derived lists with a scrambled order, errors occur because the list has been learned—that is, because participants have had the time to encode the position of each stimulus, and that positional information is then undermined by the reorganization of the list. Positional inferences are generally useful because ordered lists do not generally change their ordering dramatically. Scrambling the derived lists, as we have done, demonstrates the limits of this heuristic.

A closer analogy can be made to Paivio, Philipchalk, and Rowe (1975) observation that nonverbal factors might influence comparison of objects in long-term memory. The idea is that “item rank” in ordered lists is an abstract property of the stimulus that is learned during training and that it can be used to make judgments of order.

General Discussion

“What is learned during serial learning?” is a classic question that has preoccupied psychologists for more than 100 years (Ebbinghaus, 1885/1913). In the case of the latter, Lashley (1951) showed how such knowledge can be organized hierarchically. This question has been studied in many contexts, such as rote learning in animals (Terrace, 1984, 2005), learning lists of nonsense syllables (Bugelski, 1950; Howard & Kahana, 2002), and sentence production (Acheson & MacDonald, 2009; Chomsky, 1959). Whether performance can be adequately explained by associative mechanisms or, in addition, needs to be explained by invoking a cognitive representation of each item’s position remains a controversial question.

This study is one of the few that addresses ordinal knowledge of list items by varying the order of list items in derived lists (cf. Chen et al., 1997; Ebenholtz, 1972). In two experiments, one in which the ordinal position of items on an original list was maintained (Experiment 1), and one in which it was varied (Experiment 2), participants responded to novel pairs based on prior knowledge of both the relative and absolute positions of items in the original training lists. As shown in Figure 10, response accuracy to novel pairs for derived lists varied inversely with transposition distance. It was lowest to those pairs whose relative order was reversed.

In both of our experiments, we gave participants minimal verbal instructions, essentially nothing more than instructing them to “use the mouse to click on images and try to make correct responses.” Participants nevertheless had little difficulty performing the task.

It should be clear that our participants used two different forms of inference: positional and transitive. Even under the assumption that stimuli belong to ordered lists, and that their relative positions should therefore display transitivity, there is no logical reason that a stimulus that was in the first position on one training list should have an earlier position than one in the last position of a different list. For example, the cardinal numbers “123”, and the numbers “789”, are each ordered lists, but despite being the first in its list, “7” has a greater value than 1, 2, or 3. Without knowledge of cardinal numbers, a participant wouldn’t know the relation between the symbols on a “123” list and those on a “789” list. Nevertheless, participants in both experiments used absolute knowledge to respond to test items in derived lists. That is why “positional inference” is needed to explain their performance.

In addition, participants reliably displayed a symbolic distance effect for derived lists: The greater the spatial gap between list positions, the higher the response accuracy. Whereas positional inferences depend on absolute list position, the SDE suggests that inferences are based on relative list positions, which have classically been referred to as “transitive inferences.” It should be noted, however, that these inferences display transitivity of inferred absolute positions. In both experiments, each pair was entirely novel. Only one item on each derived came from a particular training list.

Inference as a Consequence of Representation

Our interpretation of these results is that performance reflects the manner in which ordered lists were represented. The SDE, which is commonly observed in experiments of serial learning, can be explained by a representation of an item’s position along a spatial continuum with built-in uncertainty. According to this view, the increasing error observed in proximate pairs, is the result of overlap between the uncertain distributions representing item positions (Jensen et al., 2015, 2019).

Our results are also consistent with fuzzy encoding along a spatial continuum. In new lists, items are presumed to retain their position on the continuum, even when paired with new items. Thus, our results support the belief that humans employ unified mental representations during TI (Acuna, Sanes, & Donoghue, 2002). We therefore propose that a single cognitive representation, which is both continuous and probabilistic, produces both positional and transitive inferences. This proposal is similar to the spatial coding model of lexical processing suggested by Davis (2010), albeit in a nonlinguistic context. In both models, coding of an item’s position is subject to a degree of uncertainty, especially those items that lack contextual clues.

Few previous experiments have tested performance for entire derived lists. Ebenholtz (1972) trained human participants using lists composed of 10 nonsense syllables, and tested them using two derived lists, composed of five items from the original list and five novel stimuli. For the first list, the stimuli retained their original ordinal positions, and were rapidly learned by the participants. For the second list, in which ordinal position of the retained items was changed, participants learned more slowly. Ebenholtz (1972) concluded that the first list was learned more rapidly because subjects could rely on knowledge of ordinal position, which was maintained.

The experiment performed by Chen, Swartz, and Terrace (1997), the derived list method was slightly expanded. They trained monkeys on four lists, each consisting of four arbitrarily selected items using the simultaneous chaining paradigm (reviewed by Terrace, 2005). This paradigm displays all list items during each trial, with no differential feedback provided following each response. By design, simultaneous chain performance cannot be accounted for by associative learning theories, making this procedure useful for contrasting an associative account from one depending on ordinal knowledge. After learning the original lists, monkeys were tested on four derived lists. Each derived list drew one item from each of the four training lists, resulting in combinations of items that were equally unfamiliar to the monkeys. Two of the derived lists maintained the item positions used in training. On the other two, list positions of all of the items were changed. Acquisition of the derived lists was almost immediate for the maintained lists but it was substantially slower for the changed lists. These results are consistent with those reported by Ebenholtz (1972).

Rather than using simultaneous chains, the current study presented only pairs of stimuli on each trial. This approach has been used extensively in the study of transitive inference in humans and animals (Burt, 1911; Jensen, 2017; Zeithamova, Schlichting, & Preston, 2012). McGonigle and Chalmers (1977) performed the first experiment in which TI was demonstrated in animals (monkeys). That experiment demonstrated that serial learning by pairwise presentation could be achieved by trial and error alone in animals with no capacity for language. Studies with young children (Bryant & Trabasso, 1971; Chalmers & McGonigle, 1984) demonstrated that human performance is similar to an animal’s following TI training in which there are no verbal instructions.

Because of symbolic distance effects, larger spatial differences are more easily discriminated than smaller differences. Thus, pairs that are more distantly separated are easier to discriminate than closer pairs. In addition to extensive evidence for SDEs in traditional TI designs (Jensen, 2017), we observed SDEs in derived lists as well. A possible explanation of these SDEs is that list items are represented on a spatial continuum. Items more distantly related overlap more than closely space items (Jensen et al., 2015; Terrace, 2012).

Representations based on a spatial continuum could provide an explanation for both transitive and positional inferences for derived lists. Suppose a participant learns two ordered lists, A₁B₁ … and A₂B₂ … When participants consistently respond that A₁ > B₂, they cannot be doing so on the logical basis that A₁ > B₁ and A₂ > B₂. Participants must instead be making an additional assumption, based on the absolute ordinal position of the items during training. Our results suggest that it is a combination of knowledge of absolute and relative position that produces above-chance performance and rapid acquisition of derived lists that maintained an item’s original position.

Observing that positional inferences are being used by participants does not, in itself, reveal what the underlying substrate for such inferences might be. For example, one possibility is that participants identify certain stimuli as “end markers” and encode the positions of other items relative to those markers (e.g., Henson, 1999). Superficially, this account explains the “terminal item effect” that is routinely observed in transitive inference, such that, for any given symbolic distance, performance is often highest among terminal items, and is lowest for middle items (Jensen, 2017). The difficulty with this account is that it depends on some way of unambiguously identifying which items are end markers. In ISR tasks, terminal items are self-evident from temporal cues, by virtue of a stimulus appearing at the start or end of a list. In TI, however, the only clue that an item is terminal is its relative rate of reward (100% for the first item, 0% for the last item), which cannot be judged from any single presentation.

Relational end-marker theories are particularly ill-suited to the manipulations we performed in Experiment 2, in which every list with a changed stimulus order involved changing the rank of one or both terminal items. If serial learning depended mainly on terminal landmarks, changing the rank of a terminal item should sweep the rug out from under the model, leading to decreased performance on most or all item pairs (depending on how nonterminal items relate to terminal items in the model). However, Figure 10 shows a decrease in accuracy in pairs that include an item whose ordinal position had been moved. Rather than a theory that is relative to end markers, such a result is more consistent with a theory in which every list item is encoded relative to every other list item. One way in which Henson’s (1999) landmark proposal could be made compatible with our proposal would be to assume that every item in the list is a landmark (i.e., as having an encoded position), and for every item to be subject to relative judgments. Where Henson’s (1999) model tries to identify stimuli as either absolute or relative, we argue that every stimulus position is evaluated with respect to its absolute and relative position.

Another approach is to interpret our results in terms of “analogical inference” (Gross & Greene, 2007). Under their procedure, participants learned an ordering task by trial and error using a training list, and then were asked to infer the order of items in a novel testing list. If participants carried their task representation of the ordering rule from one list to another, they could be considered to solve the testing list “by analogy” to the rule established by the training list, doing so implicitly. In this sense, “analogical inference” is broadly defined, and not necessarily limited to serial learning. We would agree that transfer of serial learning between training and derived lists (or, indeed, from one serial learning task to another, as in Jensen et al., 2013) is broadly “analogical” in the sense described by Gross and Greene (2007), as an implicit and automatic carryover of a task representation from one set of stimuli to the next. Positional and transitive inference, however, should instead be considered features of the way in which serial order is represented, and display specific properties (like distance effects) which provide information about those representations. Put another way, all demonstrations of TI via transfer tests are, at least to some degree, consistent with the idea of implicit analogical inference; however, analogical inference is too general to make specific predictions about serial learning performance; those require an understanding of how serial knowledge itself is represented.

Our results are difficult to explain by theories of reward association from the tradition of behavior analysis (reviewed by Vasconcelos, 2008). In their most basic form, theories of this type assume that participants make retrospective evaluations of the expected value associated with each stimulus, and then make comparisons of those value estimates to guide future choices. Such theories cannot account for transitive inference (specifically, for B > D preference in five-item lists) when only adjacent pairs are trained, because the stimuli B, C, and D all have equal expected values. Jensen, Muñoz, Alkan, Ferrera, and Terrace (2015) demonstrate this inability to perform TI via simulation. Jensen et al. (2019) further demonstrate that expected reward value cannot account for TI performance by varying reward magnitude directly.

To counter this criticism, more elaborate associative models have been used to explain results that appear to provide evidence of TI, notably the “value transfer model” (VTM; Wynne, 1995). Under this model, the associative value of each stimulus is “contagious,” and transfers some of its luster (or lack thereof) to the stimuli with which it is paired. Because A has an expected value of 100%, VTM proposes that the expected value for B should be somewhat greater than that of C or D because B has been paired with A in the past. Likewise, the expected value for D should be diminished somewhat because of its association with E (which, in a five-item list, is never rewarded). This contagion then propagates from item to item toward the center of each list.

In many respects, VTM can be thought of as an associative version of Henson’s (1999) cognitive model. Both rely on terminal items having a special status, and both then construct a representation of list order relative to those items. If anything, VTM appears to be a more plausible account than Henson’s (1999) model, because it allows for evaluations of all items relative to one another by the mechanism of retrospective expected value. However, such models have two shortcomings. First, behavior differs from VTM’s predictions under manipulations of the relative frequency (Jensen, 2017; Lazareva & Wasserman, 2012) and relative reward size (Jensen et al., 2019). Second, in Experiment 2, VTM makes a strong prediction that pairs with reversed orders should begin below chance, not at chance (as shown by the intercept terms in Figure 10). VTM’s downfall is its rigidity in the face of variations on the classic TI paradigm. By contrast, a cognitive-spatial approach affords enough flexibility to account for our results and those reported in the literature.

Although spatial models of serial learning show great promise, it is still difficult to account for the literature on “list-linking” effects in rhesus macaques (Treichler & Raghanti, 2010; Treichler & Van Tilburg, 1996) in terms of positional inferences. Suppose two lists, ABCDE and FGHIJ are both trained, followed by training on the “linking pair” EF. When list linking succeeds, correct inferences are subsequently made about pairs from the combined list ABCDEFGHIJ, such as favoring D in the pair DG. This constitutes a correct transitive inference, but is not the response expected from a positional inference (because “G” had a rank of 2 during training, and “D” had a rank of 4 during training). Given training on two lists, Treichler and Raghanti (2010) report that subjects appear to make erroneous positional inferences during testing when no linking pairs are trained, but make correct choices when linking pairs are included. This further suggests that, insofar as participants make assumptions about the absolute positions of items, they only do so provisionally, and are prepared to discard those assumptions if contrary information is made available. However, although list linking places important constraints on which models of serial learning may be viable, its effects have only been reported in monkeys. As such, demonstrations of list linking need to be replicated by other labs, and with other species. It is also not presently known whether human participants would link lists in the same fashion.

One limitation of the current study is the absence of information on long-term retention of the serial representations we proposed. The retention of serial representations over time (e.g., after a 24-hr period) is well-established (Terrace, 2012), but it is not clear whether subjects are able to make both positional and transitive inferences after such delays. This constitutes an interesting future direction that would build on the present results.

Another future direction is to explore the effects of item transpositions on lists of different length. Merritt and Terrace (2011) report evidence consistent with positional inference, but did so only in cases that preserved the list ordering. By building derived lists that differ in their length from those experienced in training and also manipulating the list ordering, it will be possible to make much stronger claims about the nature of the information that is encoded during training.

Implementations of Positional Inference

In part because of the difficulties inherent in proposing a coherent algorithm for cognitive models like Henson’s (1999) end-marker proposal, recent results depend instead on a kind of cognitive map that can be plausibly implemented in neural systems. In some cases, these are directly motivated by neuroimaging (e.g., Abrahamse et al., 2014), whereas others are justified more in terms of their computational properties (e.g., Cueva & Wei, 2018). Even limiting such models to those that instantiate a spatial continuum, there are still many candidates to choose from (reviewed by Kumaran, 2012). One family of plausible models has, as its core feature, some form of overlap between items with similar characteristics, and therefore takes into account the context of that change in a temporal or spatial fashion within a list of items. The most prominent example is the “temporal context model” (TCM; Howard & Kahana, 2002; Polyn & Kahana, 2008), which modifies its representation during information encoding using a “context layer,” in effect creating a gradient of similarity. Although originally intended for free-recall tasks (Kahana, 1996), TCM is flexible with regards to implementation of the context layer. Consequently, it is not a great stretch to imagine that TCM could be used to evaluate spatial distance, rather than temporal proximity.

An alternative account of the development of position and distance effects relies on generalization that arises during retrieval. The REMERGE model (Kumaran & McClelland, 2012) implements a neural network with separate layers representing individual stimuli (the “feature” layer) and pairs of stimuli (the “context layer”). When novel pairings are presented during the testing phase of a TI task, information propagates through the network to indirectly associate items on the basis of their shared contexts. This effectively implements a “configural model” (Couvillon & Bitter-man, 1992) as a neural network. For example, when the pair BD is first seen, activity flows back and forth from node to node, associating B and D along the following series of links: B ↔ BC ↔ C ↔ CD ↔ D. This approach has two important limitations, however. The first is that the simulated results described by Kumaran and McClelland (2012) make use of a neural network that is given the ordering of the adjacent pairs a priori, rather than having to learn them from feedback. As such, it has not yet been demonstrated to be able to learn list orderings from scratch. Second, such models treat each stimulus as unique unless given additional information. Given two stimuli B₁ and C₂ that belong to different training lists, no path through the network connects them unless the network is told that the pair B₁C₁ (from the first training list) and B₂C₂ (from the second training list) represent the “same context.” With no path through the network to connect B₁ and C₂, REMERGE cannot use its generalization mechanism to infer their relationship.

Computational proposals such as TCM and REMERGE are sometimes framed in the context of episodic memory. Although transitive inference is evidently ubiquitous among vertebrates (Jensen, 2017), there is still debate over whether nonhuman or nonprimate vertebrates possess episodic memories (Dere, Kart-Teke, Huston, & De Souza Silva, 2006). Another way in which these models are discussed, however, is in terms of how spatial and temporal information is processed (e.g., in the hippocampus), without necessarily invoking episodic memory. Until a consensus is reached about how the brain processes episodic memories t, if at all, in nonhuman animals, we prefer to interpret these neural networks as candidate models for spatial/temporal computation in the brain. Given the similarities between human and nonhuman performance on other serial tasks (Terrace, 2012), tasks that rely on various forms of inference about serial order provide a rich source of evidence not only for the cognitive mechanisms in human inference, but for evolutionary precursors of those faculties that are shared with other species. Once computational models of serial learning are developed that are able to give a good accounting of the results we have reported in this study, those models will provide a potential window into those memory mechanisms that we share with other vertebrate animals.