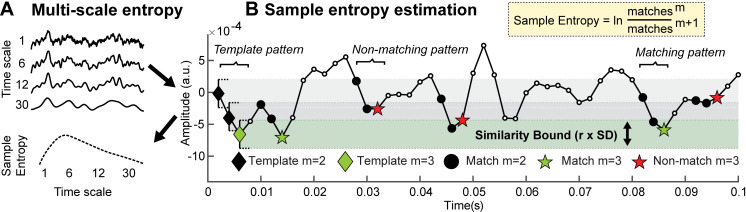
Fig 1. Traditional MSE estimation procedure.
(A) Multi-scale entropy is an extension of sample entropy, an information-theoretic metric intended to describe the temporal irregularity of time series data. To estimate entropy for different time scales, the original signal is traditionally ‘coarse-grained’ using low-pass filters, followed by the calculation of the sample entropy. (B) Sample entropy estimation procedure. Sample entropy measures the conditional probability that two amplitude patterns of sequence length m (here, 2) remain similar (or matching) when the next sample m + 1 is included in the sequence. Hence, sample entropy increases with temporal irregularity, i.e., with the number of m-length patterns that do not remain similar at length m+1 (non-matches). To discretize temporal patterns from continuous amplitudes, similarity bounds (defined as a proportion r, here .5, of the signal’s standard deviation [SD]) define amplitude ranges around each sample in a given template sequence, within which matching samples are identified in the rest of the time series. These are indicated by horizontal grey and green bars around the first three template samples. This procedure is applied to each template sequence in time, and the pattern counts are summed to estimate the signal’s entropy. The exemplary time series is a selected empirical EEG signal that was 40-Hz high-pass filtered with a 6th order Butterworth filter.