Figure 2.

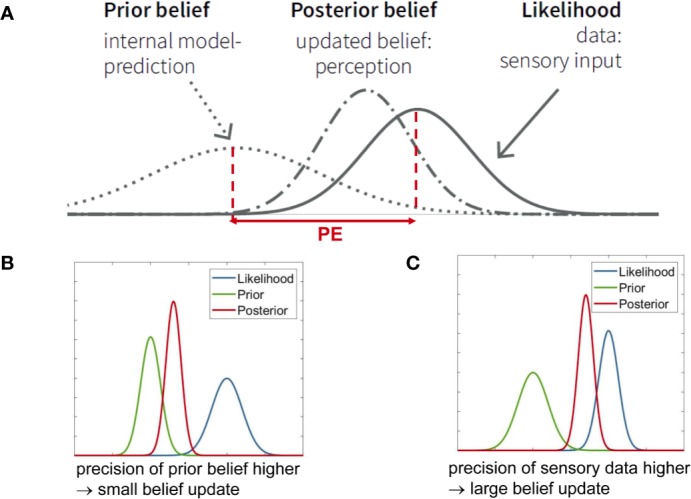
(A) Graphical summary of Bayes’ theorem (see Eq. 1) for the case of Gaussian probability distributions. It illustrates that the posterior represents a compromise between prior and likelihood, depending on their relative precision. PE is the abbreviation for “prediction error.” To revisit the example from Figure 1B, let us consider perception of temperature. The actually perceived temperature (posterior belief) is a compromise between the expected or predicted temperature (prior) and the sensory input (likelihood). The posterior belief can also be understood as updating the prior belief, where the magnitude of the belief update depends on the prediction error (PE) and the relative precisions (inverse variance) of the prior and the likelihood. In this example, the precision of sensory input (likelihood) is higher, therefore the posterior is closer to the likelihood. This panel is adapted from Figure 2 in Haker et al. (82), with permission. (B) When the precision of the prior belief is higher than the precision of the data (likelihood), a small belief update results, i.e., the posterior stays close to the prior. (C) When the precision of the data (likelihood) is higher than the precision of the prior belief, a large belief update results, i.e., the posterior moves more strongly towards the data.