Abstract
The spatial organization of cardiac muscle tissue exhibits a complex structure on multiple length scales, from the sarcomeric unit to the whole organ. Here we demonstrate a multi-scale three-dimensional imaging (3d) approach with three levels of magnification, based on synchrotron X-ray phase contrast tomography. Whole mouse hearts are scanned in an undulator beam, which is first focused and then broadened by divergence. Regions-of-interest of the hearts are scanned in parallel beam as well as a biopsy by magnified cone beam geometry using a X-ray waveguide optic. Data is analyzed in terms of orientation, anisotropy and the sarcomeric periodicity via a local Fourier transformation.
1. Introduction
The contractile function of the heart relies on an intricate structure spanning multiple length scales: starting with the molecular scales of the myosin motors and the actomyosin assembly, the formation of the sarcomeric units and myofibrils, to the cellular scale of single cardiomyocytes, arrangement of myocyte chains embedded in connective tissue, all the way to the aggregation of cardiomyocyte chains forming a complex cardiac mesh and finally the scale of the entire organ [1]. While the macroscopic architecture of heart muscle is known for more than hundred years from classical anatomy and histology, the detailed three-dimensional (3d) arrangement of muscle cells and myofibrils cannot be reconstructed from histology alone, due to the invasive nature of sectioning [2]. Different models for the description of cardiac architecture are therefore still under intensive debate [3,4]. With recent advances in medical imaging techniques, most notably magnetic resonance imaging (MRI) and ultrasound, the 3d structure of the heart can now even be imaged dynamically, however, not at a resolution to resolve the complete network down to the level of a single muscle cell [5,6].
With the advent of phase-contrast micro-CT and improvements in data acquisition and reconstruction, it has now become possible to characterize the entire heart with voxel sizes in the range of a few micrometers using synchrotron radiation [7–12], or even laboratory x-ray sources [13]. These results indicate that the heart is a complex 3d mesh of aggregated cardiomyocytes with a supporting fibrous matrix [1,4]. In contrast to conventional x-ray imaging which is based on absorption and shows little contrast for heart tissue in the absence of heavy metal staining [14–16], phase contrast tomography exploits the intrinsic density variations within the tissue. These small spatial variations of electron density determine the real-valued decrement of the x-ray refractive index , which is from 1 up to 3 orders of magnitude larger (depending on tissue composition and wavelength ) than its imaginary part which accounts for absorption. Phase-contrast x-ray imaging can hence visualize even small features down to cellular and sub-cellular scale for heart tissue biopsies [17]. At the same time, molecular structures of acto-myosin networks can be probed in thin heart sections by scanning diffraction with micro- and nano-focused beams [18,19], also in combination with coherent imaging and correlative super-resolution microscopy [20,21]. However, the acquisition time and dose of scanning diffraction would be prohibitive for 3d imaging of the whole heart, making it preferable to use full-field illumination and phase contrast CT to study the arrangement of cardiomyocytes within the heart.
While the orientation, degree of filament alignment and thickness of individual muscle bundles in the whole organ can be roughly estimated by sub-volume based algorithms also for laboratory CT data, the contrast and resolution are insufficient to make accurate statements about single myofibrils [8,13,22].
In this work, we present a multi-scale approach to phase contrast CT of heart tissue, combining whole heart overview scans of voxel size µm with region-of-interest (ROI) scans acquired at voxel size nm, and even nm by means of cone beam magnification. In a proof-of-concept experiment involving three levels of magnification we probe unstained fixed hearts of wild type mouse, comparing paraffin and ethanol embedding. To preserve image sharpness and to obtain quantitative density reconstructions, we use iterative phase phase retrieval algorithms [23,24], which do not follow the conventional linearization schemes. These algorithms either work at large Fresnel number and linearize the contrast in terms of the defocus distance [25,26] or use linearization of the optical properties of the sample [27]. We then use reconstructed 3d data to characterize the structural orientation and degree of alignment of the heart tissue by an algorithm based on the local structure tensor [13,22]. In order to extract the sarcomeric periodicity from the high-resolution data, a local Fourier-analysis of the electron density was used [13].
We implement this approach by an illumination scheme based on three different configurations of the Göttingen Instrument for Nano-Imaging with X-Rays (GINIX). The different configurations allow to image field of views (FOVs) with a range from several mm to a few hundred micrometer and are characterized by the profile of their wave front. For overview scans of the heart with high photon flux, we introduce a configuration based on the illumination of a pair of Kirkpatrick-Baez mirrors (KB). This setup enables to capture a FOV of about 77 with an effective pixel size of 3.25 µm. Higher resolution was achieved by illumination of the sample using the natural divergence of the undulator in a parallel beam (PB) geometry. With this configuration for ROIs with a size of about 1.61.4 were probed with high photon flux and an effective pixel size of 650 nm. In order to resolve the sarcomeric structure of the heart tissue, the cone beam geometry of a waveguide (WG) illumination was used. This configuration, with a scalable geometric magnification , enables high-resolution scans of a biopsy punch with an FOV of few hundred µ and an effective pixel size of less than 200 nm.
2. Experimental approach
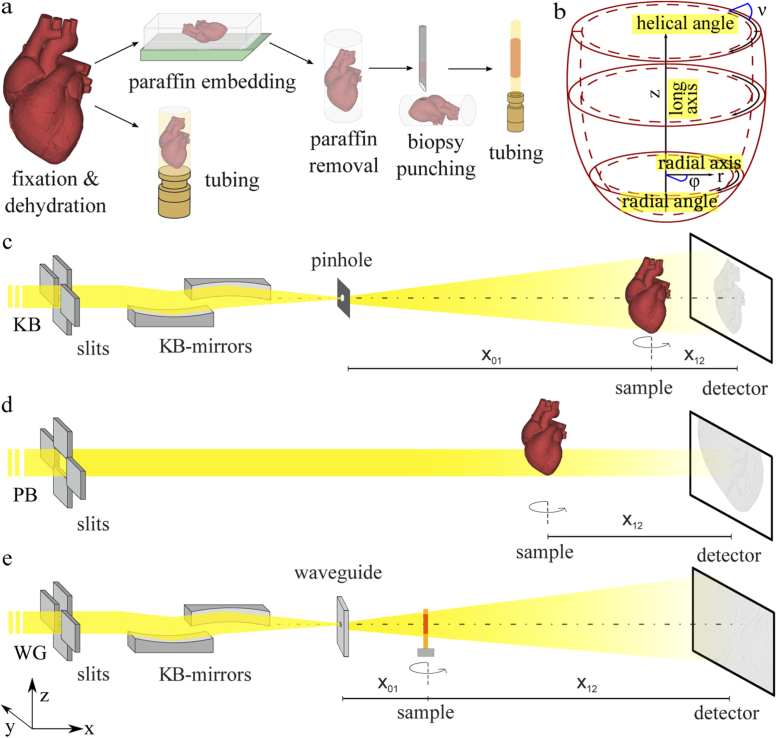
The goal of this work is to study the structure of murine heart tissue on multiple length scales from the level of the whole organ down to the (sub-cellular) sarcomeric level. This requires a very particular experimental approach involving different optical schemes for the illumination with synchrotron radiation, as detailed below. The corresponding sample preparation and the experimental setup are sketched in Fig. 1. While the whole heart scan with FOV µm as well as the ROI scan with FOV 1 µm were acquired on an entire unsliced paraffin-embedded mouse heart, the high-resolution data set with FOV nm was recorded from a mm biopsy obtained from the paraffin block after the first two scans. For comparison, an ethanol-embedded heart was also scanned at large FOV and intermediate FOV.
Fig. 1.
(a) Schematic visualization of the sample preparation. Explanted hearts were fixed in 4% formaldehyde solution, and dehydrated in an increasing series of ethanol. One heart was stored in ethanol and the second organ was embedded in paraffin. Excess paraffin was removed with a scalpel. For high-resolution measurements, a biopsy was taken and placed in a polyimide tube. (b) Sketch of the coordinate cylindrical system for the description of the structural characterization. The long axis z is positioned in the center of the left ventricle and structural orientation can be parameterized by the radial plane defined by and and the helical angle . (c) Experimental setup with KB illumination for overview scans with an FOV of several . The beam is focused by a pair of KB mirrors and cleaned by a pinhole with a diameter of 3 µm. The sample tower is placed at distance . Projections are taken at distance behind the sample. (d) Experimental setup with parallel beam illumination for ROI scan with an FOV of about 1 . Projections are taken with a microscope detection system at distance . (e) Experimental setup with waveguide illumination for high resolution scans of tissue biopsies with an FOV of a few hundred µm. Due to the cone beam geometry, the magnification can be scaled by the source-sample distance . Projections are taken at distance behind the sample.
Sample preparation: Freshly explanted hearts from two male 16 weeks old wildtype C57BL/6 mice were fixed in 4% formaldehyde solution for 24 hours. The fixed hearts were then dehydrated in an increasing series of ethanol. In order to determine structural differences depending on sample preparation, the first organ was stored in 100% ethanol solution and the second organ was washed in 100% xylene solution and embedded in paraffin. To decrease x-ray absorption, excess paraffin was removed with a scalpel. For high-resolution measurements, a biopsy with a diameter of 1 mm was taken and mounted in a polyimide tube. The structural orientation was analyzed and described in the coordinate system shown in Fig. 1(b).
Synchrotron instrument: Data were acquired at the Göttingen Instrument for Nano-Imaging with X-Rays (GINIX) at the P10 beamline of the PETRA III storage ring at DESY (Hamburg, Germany). The endstation is dedicated to coherent nano-diffraction with focused undulator radiation, and in particular high-resolution holographic imaging using KB-waveguide compound optics [28,29]. As a full-field technique it is ideally suited for tomography of extended samples such as biological tissue [30]. The m long undulator (U29) creates an x-ray source of about 85 µm 14 µm (FWHM, horizontal vertical) with a divergence of 28 µrad × 3.7 µrad (1, h v). For the scans at large and intermediate FOV, a photon energy of keV was chosen by a double crystal Si(111) monochromator. For the high-resolution scan on the heart biopsy, the energy was changed to keV to increase interactions between wavefront and sample. The GINIX endstation is located about 87 m behind the source. For x-ray tomography this endstation can be operated in three different geometries which enable different resolutions and a multi-scale analysis, covering samples sizes with an FOV ranging from several down to a few µ } . The different configurations are characterized by their illumination optics and wavefront:
-
1.
Kirkpatrick-Baez mirror (KB) illumination: Configuration for overview scans with high photon flux and an effective pixel size of 3.25 µm and FOV of about 87 .
-
2.
Parallel beam (PB) illumination: Configuration for the region of interest (ROI) scans with high photon flux enabling an effective pixel size of 650 nm and an FOV of about 1.61.4 .
-
3.
Waveguide (WG) illumination: Setup with a scalable geometric magnification for high-resolution scans with an FOV of a few hundred µ and an effective pixel size of less than 200 nm.
A sketch of the different geometries is shown in Fig. 1(b)-d. The three experimental setups, the acquisition and the handling of the data is described in more detail below.
2.1. KB illumination
Since the natural divergence of the undulator beam is too small in order to reach a sufficiently large beam size to cover entire mouse heart even at m, the beam is focused by a pair of KB mirrors. The KB focus then serves as a secondary source with a much higher divergence and hence a beam size which is easily adjusted by the defocus position. Since the KB reflectivity is about 95% , this scheme almost preserves the full flux impinging onto the mirrors with 400 µm active area (entrance pupil). In this work, the spot size in the KB focus was about nm nm (FWHM, h v), as measured by waveguide scans through the focus. The size of the illumination area is then simply given by divergence of the KB beam, which is about 2.0 mrad 1.3 mrad and the defocus distance m yielding FOV = 10.2 mm 6.6 mm (). The height deviation from the ideal elliptic profile and residual roughness of the KB mirror surface result in a pronounced pattern of vertical and horizontal stripes in the illumination wavefront, which impedes the empty beam correction [31–34]. In order to smoothen the wavefront and to remove these high-spatial frequency contributions, a pinhole with a diameter of 3 µm (tungsten, thickness 300 µm) was placed in the KB-focus. The pinhole acts as a spacial filter in reciprocal space and smooths the intensity variations in the detector plane.
The sample was mounted on a sample stage (SmarAct GmbH) at distance cm upstream from the detector plane. For the alignment of the sample respective to the axis of rotation, two compact linear piezo positioners are used on top of the rotation stage. The rotation axis was aligned with respect to the illumination using an -translation below the rotation. Furthermore, the whole stage was mounted on an aluminum plate which could be manually tilted by four adjustable screws to align the tomographic nick angle. Projections were recorded using an imaging system (Optique Peter) equipped with a 50 µm LuAG scintillator and an objective revolver (2x, 4x or 10x) coupled to a sCMOS camera (PCO edge 5.5, 2560 2160 pixels) with a physical pixel size µm. The detector stage is also described in the Fig. 7.
The geometry of the KB-illumination has a low geometric magnification with , but enables a relatively large FOV. Using the 2x objective resulting in an effective pixel size of 3.25 µm, projections of a whole mouse heart can be acquired in a single scan. For tomographic reconstruction, 2001 projections over 180 degrees with an acquisition time of 1 s were recorded. Additionally, 100 empty projections were acquired before and after each tomographic scan. All acquisition parameters are given in Table 1.
Table 1. Data acquisition parameters for the three different geometries: (KB) broadened beam after focusing by KB-mirrors for whole organ, (PB) Parallel beam, (WG) waveguide setup for holo-tomography at high geometric magnification.
| illumination | KB | PB | WG |
|---|---|---|---|
| photon energy (keV) | 13.8 | 13.8 | 8 |
| source-sample-dist. (m) | 5.06 | 88 | 0.12 |
| sample-detector-dist. (m) | 0.34 | 0.22 | 4.98 |
| effective pixel size (µm) | 3.25 | 0.65 | 0.1675 |
| field-of-view () | 8 7 | 1.6 1.4 | 0.42 0.36 |
| acquisition time (s) | 1 | 0.035 | 1 |
| number of projections | 2001 | 1500 | 1500 |
| number of flats | 200 | 150 | 50 |
The spatial filtering of the illumination wavefront by the pinhole facilitates empty beam division without strong artifacts. Only some impurities of the scintillator occasionally led to overexposed and saturated pixels, which were removed by a median filter. However, small variations in the empty-beam divided near-field pattern remain since the illumination shifts slightly between the time of recording of the image and empty beam, respectively. To account for this, a suitable empty beam was generated for each projection by a linear combination of empty beam basis functions, generated by principal component analysis (PCA) from the pre- or post-recorded stream of empty beam patterns. The processing of the projections acquired at the KB configuration is also shown in Fig. 8.
2.2. Parallel beam illumination
For ROI scans with higher resolution, the second configuration sketched in Fig. 1 was used. The sample tower is roughly in the same location as for the high resolution KB-waveguide configuration (configuration # 3, see below), but the KB is moved out by a few millimeters to use the primary beam without focusing. With slits fully opened, the beam size (FWHM) as defined by the divergence is about 5.8 mm 0.77 mm (h v) at the position of the endstation about 88 m behind the undulator source. In the vertical directions, all beamline slits are opened to exploit the natural beam size of the undulator beam at the position of the endstation; the horizontal slits were adjusted to fill the detector. The sample was placed on a completely motorized tomography stage with an air bearing rotation stage (UPR-160 Air, Micos, Germany). Due to the accuracy and reproducibility of the rotation, it is possible to acquire projections in a continuous scan, i.e. projections with a short acquisition time are taken while the sample is rotated continuously. For the data shown here, projections were recorded with the microscope camera system described above with a 10x objective at distance cm behind the sample. In this work, we focused especially on the area near the apex of the heart. Over 180 degrees 1500 projections with an acquisition time of 0.035 s were acquired. In continuous scan mode, the acquisition time for one tomogram was 75 s. Before each tomography scan, empty projections were taken.
Due to the high stability of the illumination, it was not necessary to correct the flat field by a PCA approach. The flat field was computed by a median of all recorded empty projections. The processing of the projections acquired within parallel beam geometry is illustrated in the top row of Fig. 9.
2.3. Waveguide illumination
For imaging of the cardiac tissue with sub-cellular resolution, a biopsy of the heart tissue near the apex was taken from the previously scanned heart and investigated by holographic tomography using the cone beam geometry with WG illumination, i.e. configuration # 3 (see Fig. 1(e)). In this geometry, a waveguide is positioned in the focus of the KB mirrors. X-rays are coupled into the waveguide channel which acts as a spatial and coherence filter, similar to the pinhole of the KB setup but with a lateral confinement of nm. Therefore, no artifacts from preceding optical components are visible and the empty beam intensity profile is smooth and Gaussian shaped. The small secondary source size at the exit of the waveguide and the high coherence of the WG illumination enables high geometric magnification which can be scaled by changing the source sample distance . Projections were recorded with a sCMOS Camera (2560 2160 pixel) with 15 µm Gadox scintillator and a physical pixel size of 6.5 µm (Andor). The biopsy was scanned with an effective pixel size of 167.5 nm, 1500 projections over 180 degrees, and acquisition time of 1 s.
The flat field was created by the PCA analysis explained above. Additionally, the low frequency intensity variations of the background were corrected by Gaussian filtering. The processing of the projections acquired with in WG geometry is also illustrated in in the bottom row of Fig. 9.
2.4. Phase retrieval and tomographic reconstruction
For all projections, recorded at the three different configurations of the endstation, phase retrieval was performed after the empty beam correction. To this end, we first inspected data by linearized phase retrieval according to the contrast transfer function (CTF) algorithm. To this, the approximation of a homogeneous object was used, specifying the phase distribution in the object plane by
| (1) |
with natural units for the (squared) spatial frequencies, measured intensities in the detector plane , ratio of imaginary and real part of the refractive index , and a frequency-dependent regularization parameter . The results of the CTF then served as an initial guess for subsequent iterative phase retrieval based on a nonlinear Tikhonov approach, which does not require the assumption of a weakly varying phase. Further, additional object constraints such as range constraints for the phase shift can be included [35]. The method can be regarded as a nonlinear generalization of CTF phase retrieval, and for a weakly phase-shifting sample (linear approximation) without further constraints, both approaches yield exactly the same result. The minimization of the Tikhonov-functional is implemented by a gradient-descent method with adaptive step sizes [35].
The parameters of the phase retrieval were selected manually, optimizing contrast for tissue and paraffin. They are shown in Table 2. If anomalous refraction effects can be neglected (far from absorption edges), the phase shift in the sample exit plane is directly proportional to the projected electron density . Hence, if the phase shift is with respect to the beam passing at the side of the object in air, the projected electron density can be obtained. For ROI tomography, the density values correspond to excess electron density with respect to the (average) medium defined by the object, i.e. it can be both positive and negative. Further complications arise from the fact that phase retrieval of inline holography is often hampered at small spatial frequencies. The retrieved electron density must therefore be interpreted with caution and should in most cases be regarded as an effective excess density. Nevertheless, it is instructive to express the obtained values in terms of electrons per unit volume. After reconstruction by the inverse Randon transform, we therefore compute the local electron density from the phase shift induced by each voxel length as
| (2) |
with wavelength and classical electron radius. For the tomographic reconstruction of the volumes the Astra toolbox with filtered back projection was used [36,37]. Additionally, ring removal (wavelet and additive ring removal) was performed following [35,38].
Table 2. Parameters of the phase retrieval using the nonlinear-Tikhonov approach of the CTF.
| illumination | KB | PB | WG |
|---|---|---|---|
| Fresnel number | 0.3240 | 0.0216 | 0.0015 |
| ratio | 1/35 | 1/35 | 1/80 |
| 3 | |||
| 0.1 | 0.05 | 0.2 | |
| maximal phase shift | 0 | 0 | 0 |
| maximal number of iterations | 100 | 100 | 100 |
3. 3d heart structure on different length scales
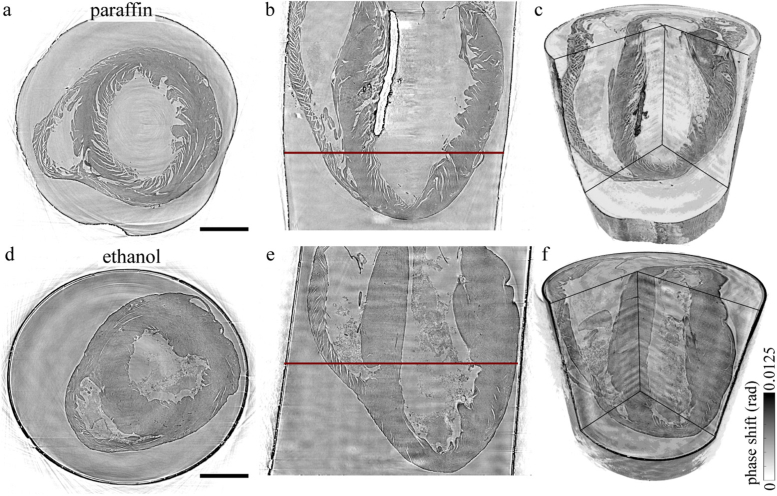
Figure 2 shows the tomographic reconstruction of the whole heart scans acquired with the KB illumination. In the top row, the reconstructed volume of the paraffin-embedded heart is depicted, and in the bottom row the reconstruction of the heart stored in ethanol. For both preparations, a transverse, a sagital slice and a rendering of the reconstructed volume are displayed. In terms of data quality (i.e. quality of phase retrieval and tomographic reconstruction), the paraffin-embedded sample exhibits less low frequency artifacts, which appear especially in the sagital slice Fig. 2(e) of the reconstruction of the heart in ethanol solution. This can be attributed to the better performance of the PCA analysis for the empty field correction. There were fewer variations in the illumination during the recording of the solid embedded heart, and also slight movements of the liquid embedded sample may have occurred. Note that motion artifacts are to be expected if the heart is not mounted tightly inside the tube, or if bubbles form due to the energy transfer from the radiation [39]. Furthermore, the fact that the x-ray absorption of the ethanol is higher and causes a higher difference between the empty illumination profile and the respective projection may have had an influence. However, whole heart phase contrast tomography in this configuration is possible for paraffin and liquid embedded hearts, showing a way to scan large tissues exceeding the natural beam width with brilliant undulator radiation and at small acquisition time.
Fig. 2.
Three-dimensional structure of the murine hearts acquired with the KB illumination. The top row: tomographic reconstruction of the paraffin-embedded heart, bottom row: tomographic reconstruction of the heart in 100% ethanol solution. From left to right a transverse and a sagital slice of the reconstructed volume and a volume rendering of the samples is shown for both sample preparations. The reconstruction of the paraffin-embedded sample yields fewer artifacts, due to a more stable flat field correction. However, the cardiac structure of the heart in 100% ethanol solution is better conserved. Scale bar: 1 mm.
With this configuration the influence of sample preparation on the integrity of the specimen was analyzed. The overall structure of the heart tissue can be well identified for both preparations, however, with differences characteristic for sample preparation. By comparing the tomographic results of both reconstructions shown in Fig. 2, there is no noteworthy difference in the size of the hearts. However, differences in data quality and in preservation of the cardiac structures were observed. The signal-to-noise (SNR) was determined for the given slices of both preparations by
| (3) |
with the difference of the mean intensities of tissue and surrounding medium in a ROI of 100100 px and the standard derivation of the intensities in the medium . For paraffin embedding a SNR of 8.3 and for storage in 100% ethanol solution a SNR of 4.2 was determined. The tissue is significantly more homogeneous for the case of liquid embedding, while paraffin embedding results in pronounced fissures and ruptures between single muscle bundles. The fact that the integrity of the cardiac tissue is better preserved by the ethanol fixation could be explained based on changes associated with washing in xylene and subsequent exposure of the tissue to heat during the transfer to the liquid paraffin. This standard procedure can result in a removal of lipids and fatty acids which might contribute to increased spacing within the myofibrils. Furthermore, the small air bubbles in the ventricle, which can be identified as the dark region in the left ventricle (LV) in the volume rendering in Fig. 2(c), cause scattering and lead to artifacts in the phase reconstruction near the bubble. At the same time, tissue in paraffin offers higher contrast for single muscle bundles and allow a better identification of the myocyte orientation. The ethanol-embedded heart with almost no visible ruptures in the myocardium and a larger amount of erythrocytes in the ventricles is more challenging in view of the CT measurement, but cardiac structures are still clearly revealed, in line with literature results at 20 keV [12]. Altogether, this geometry was well suited to acquire a fast overview scan of the whole heart with a resolution below 10 µm.
To resolve smaller tissue structures, the hearts were scanned with the configuration using PB illumination. For these measurements no further preparation of the sample was necessary. The ROIs were identified based on the overview scans. For the paraffin-embedded sample, a biopsy near the apex was taken and analyzed using the WG configuration with cone beam geometry.
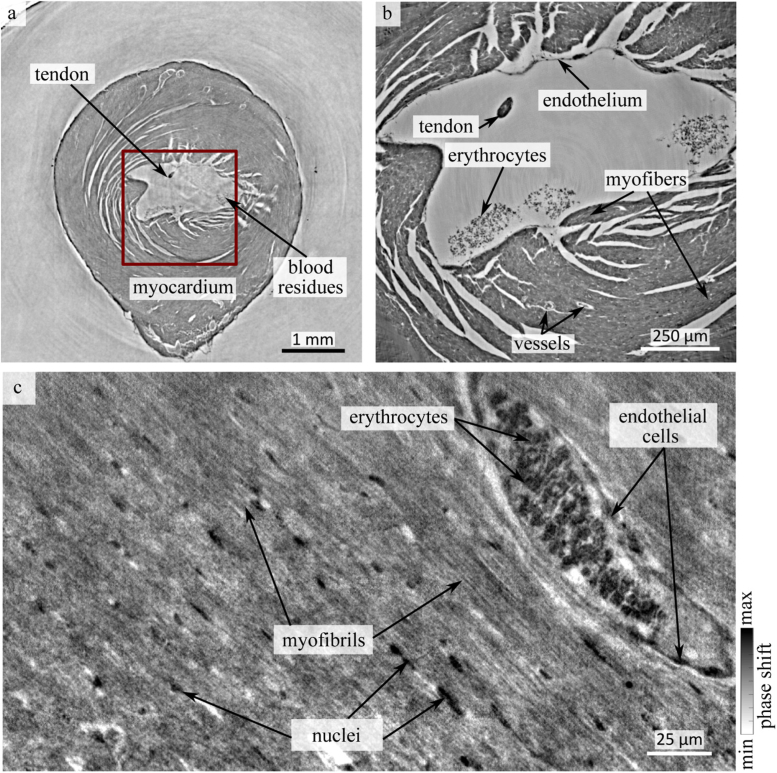
Figure 3 shows the results of the tomographic reconstructions for the paraffin-embedded heart, based on the three different modalities of the beamline setup. In Fig. 3(a), a slice near the apex of the heart from the overview scan is shown. Besides the myocardium and some ruptures along the bundles of myocytes, the single cell layers of endo- and epicardium as well as some blood residues and a tendon within the left ventricle were identified. The red box indicates the area in which a ROI scan was recorded with PB illumination. The corresponding slice is shown in Fig. 3(b). In this scan, more details of the tissue structure were resolved. For instance, a small vessel, most likely an an oblique section of a venule, containing erythrocytes with a wall that is lined by an exceedingly thin single sheet of endothelial cells, are visible. Sub-cellular structures of the cardiomyocytes, such as the nuclei, starts to appear in the reconstruction. The typical elongated shape of the nuclei is also clearly visible as black dots within the myocardium. Moreover, the orientation of the cardiomyocyte chains becomes visible.
Fig. 3.
Reconstruction of the cardiac structure of a paraffin embedded heart on multiple length scales. (a) Slice of the tomographic reconstruction acquired by KB-illumination with an effective pixelsize of 3.25 µm. The coarse interior structure can be identified, but smaller details such as small vessels and sub-cellular features are below the resolution of the setup. The red box marks a ROI of a scan with the PB illumination which is shown in (b). Erythrocytes and a layer of cells of the endothelium can be identified at this magnification. (c) In order to image sub-cellular features such as myofibrils, a biopsy of the heart was scanned at high resolution with the WG optic. In this geometry, details such as a small vessels filled with erythrocytes, endothelial cells, and nuclei in between myofibrils become visible.
Fig. 3(c) shows high resolution data acquired with the WG configuration. This geometry allows identification of sub-cellular structures such as nuclei, erythrocytes and myofibrils. In the given slice, also a blood vessel with a layer of endothelial cells is visible.
Based on the tomographic reconstructions, the orientation of the cardiomyocytes within the heart tissue was analyzed. The procedure and the results of the analysis of the structural organization will be described in the next section.
4. Orientation of the cardiac structures
The structural orientation of the cardiac tissue (here essentially the cardiomyocytes chains) can be extracted from the reconstructed electron density using an approach which is based on the gradient-based structure tensor [8,13,22,40]. A detailed description of the analysis is given in [40]. A small sub-volume with edge length (cubic box with sidelength of voxels) is chosen around the central pixel of the sub-volume. is defined by the first derivatives of the reconstructed (electron) density
| (4) |
where the matix entries are products of the partial derivatives along i and j, or more precisely the box averages thereof. From the eigenvalue problem
| (5) |
three eigenvectors and eigenvalues can be determined, representing the structural orientation averaged over the sub-volume, which is subsequently shifted throughout the entire volume. The direction of fiber symmetry is defined by the eigenvector with the smallest eigenvalue.
In addition, the tissue anisotropy, i.e. local degree of orientation, is quantified in terms of an order parameter defined as
| (6) |
with and the diagonalized . For perfect isotropy we get , while is obtained in the limit of perfect fiber-like alignment. Hence, describes the degree of orientation within the tissue. In order to save computational power, the orientation parameters can be calculated for areas containing cardiac structures, while voxels containing air or paraffin are masked out, based on their gray value. Only areas containing tissue are shown.
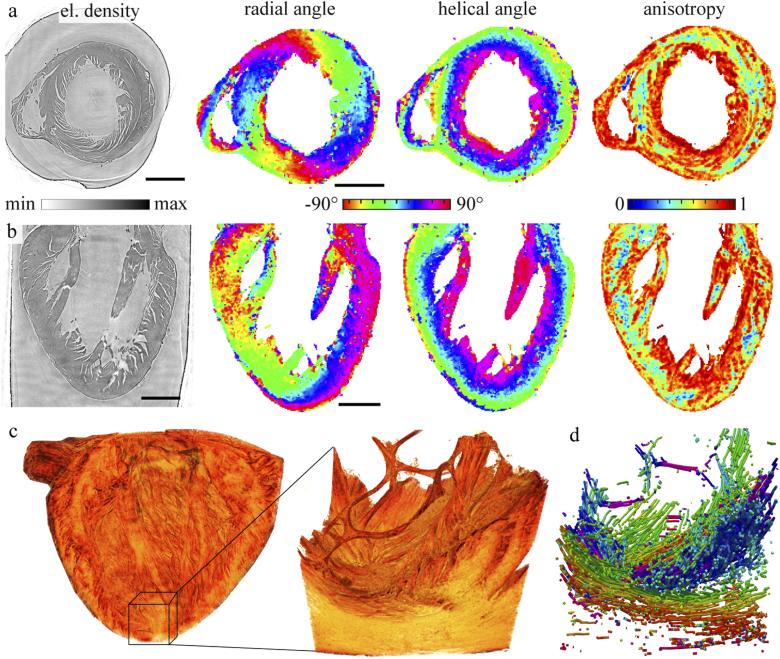
Figure 4 shows the reconstruction of the myocyte orientation of the paraffin-embedded heart. The top two rows show the reconstructed phase, the radial and helical angle and the anisotropy of two orthogonal slices. The circular alignment of the muscle bundles, which clearly appears in the phase reconstruction of the transverse plane, is corroborated and quantified by the radial angle obtained form the . The radial direction is oriented continuously around the left ventricle and is almost point symmetrical with respect to the center of the lumen. The helical angle, describing the elevation of the cardiac orientation from the radial plane, is directed along the long axis in the area around the left ventricle. Apart from the internal structure of the tissue, a significant contribution to the and resulting anisotropy must be attributed to interfaces created the detachment of the myocytes aggregates and by fissures associated with the standard procedure of paraffin embedding. However, the interfaces do not seem to form arbitrarily, but preferentially follow the muscle myocyte. For this reason, we consider the results to still give a reasonable portrait of the cardiac structure. Note that the results of the ethanol-embedded heart are hardly affected by this complication, and can hence serve as benchmark for the results. For the paraffin embedded heart the mean anisotropy was determined to . As expected it is higher than the mean anisotropy of the heart in ethanol solution with . Next, the (pseudo-)vector field describing the myocyte orientation was further analyzed by a stream tracing algorithm which treats the data effectively as a flow problem probed by tracer particles [41]. This can help to visualize the long range connectivity of muscle tissue. The analysis was performed on a ROI probed by the PB configuration, as shown in Fig. 4(c), resulting in data visualized in Fig. 4(d). Future extension of such work could be directed at establishing the relationship between the connectivity of cardiomyocytes and the signal propagation of excitation waves.
Fig. 4.
Orientation of the cardiac tissue for the paraffin-embedded heart. (a) Transverse and (b) sagital slice through the reconstructed volume, showing (from left to right) reconstructed density (proportional to phase) in gray value, radial angle, helical angle, and anisotropy parameter , as computed based on the local structure tensor. (c) Volume rendering of the whole heart (KB illumination) along with a ROI near the apex (PB illumination). The orientation was determined in the same way as for the overview scan. (d) A stream tracing algorithm [41] applied to the vector field to visualize the 3d alignment of the cardiomyocytes. The radial orientation color is coded as in the orthogonal slices shown above. Scale bars: 1 mm.
In a next step, the ethanol-embedded heart was analyzed at higher resolution, based on the PB configuration. To this end, a ROI near the apex was chosen. Compared to the paraffin embedding, the ethanol embedding enables better preservation of cardiac structure, see also Fig. 2.
Figure 5 shows the myocyte orientation of the ethanol-embedded heart as a result of the structural analysis, with Fig. 5(a) the volume rendering of the reconstructed density. Note, that the blood residues near the apex are masked out, based on a threshold in anisotropy, which excludes the connected area with values of . In addition, small holes in the mask were closed. Four representative and equidistantly spaced slices, located just below the left ventricle blood pool are presented. Slice in Fig. 5(b) is shown at large to give an impression of the structural details visible in the data. Notably, the dense organization of cardiomyocytes, nuclei and small blood vessels can be recognized. Aside the density distribution, anisotropy as well as helical and radial angle of the cardiac network were again analyzed, see the examples shown in Fig. 5(c-e). The position of all slices in the volume is marked by dark red line in Fig. 5(a). Note that the determination of the structural parameters is based on a sub-volume around each pixel of the phase reconstruction. Therefore, the structures in the anisotropy and angle maps may appear slightly larger than in the two dimensional slice.
Fig. 5.
Orientation of the cardiomyocytes near the tip of the left ventricle, shown for the ethanol-embedded heart. (a) Volume rendering of the heart tissue, with (b) a representative transverse slice through the reconstructed density. The location of the slice is marked as a red line in the volume rendering. Details as small vessels and nuclei can be identified in the dense arrangement of cardiomyocytes. Further, on the left of the 3d volume one bundle of cardiomyocytes is highlighted. (c-e) Further slices through the reconstruction volume are located below the left ventricle and consecutively shown from apex upwards. For each slice, the density, anisotropy, modulus of the helical angle and radial angle are plotted. The locations of the slices are also marked as dark red line line in (a). The white asteroid in the display of the helical angle marks a muscle bundle which is oriented in the direction of the long axis. The black arrow in (c) indicates a vortex of the cardiomyocyte arrangement. Scale bar: 250 µm.
The anisotropy indicates a clear alignment of the cardiomyocytes, especially for the regions around the ventricle, where some gaps between the cells can be identified. But also within the dense tissue some, areas of high anisotropy are encountered. For regions with no preferable directions as for the blood residues, the anisotropy is very low. As explained in the previous paragraph, the areas of no significant alignment have been masked out for the display of the corresponding angles. Next to the anisotropy, the absolute value of the helical angle is shown. Blue areas indicate an in-plane orientation while purple indicates an alignment towards the long axis. On the right of each row in Fig. 5, the radial angle is shown. It indicates a vortex evolving below the left ventricle (see black arrow). From the combination of both angular representations, areas of different orientations can be identified. These correspond to chains of cardiomyocytes which are oriented in the same direction. For example, one muscle bundle which is oriented towards the long axis is located in the bottom left of the ROI (see asterisk). This bundle of cardiomyocytes is also highlighted in the 3d volume rendering Another bundle in this region (directly next to the lumen) is oriented in the radial plane in the slice shown in Fig. 5(d). However, inside these areas of structural alignment some irregularities appear. For example, in the representation of the helical angle in the slice shown in Fig. 5(e) a band of irregularities appears in the myocardium. This may indicate an entanglement of the cardiomyocytes similar to a mesh-like structure. These small details were not recognized at lower resolution, i.e. in the KB data.
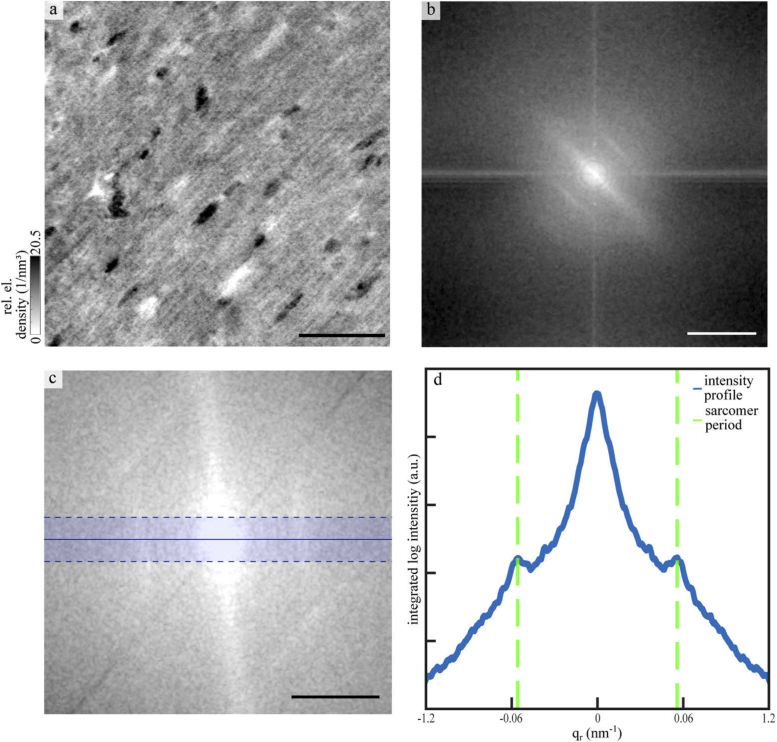
Figure 6 shows that the sarcomeric periodicity can be extracted from the high resolution data (WG optic). To this end, a cubic sub-volume, containing mostly tissue and no blood vessels, with an edge length of 600 px was selected from the tomographic reconstitution and probed by a Fourier analysis. In Fig. 6(a) a maximum projection over 20 layers of the sub-volume is displayed. The corresponding (central) slice of the 3d Fourier space is shown in Fig. 6(b). Orthogonal to the myofibrils, a pronounced streak is observed indicative for a broader distribution of inter-myofibril distances. The sarcomeric periodicity, oriented perpendicular to the myofibrils, is encoded in the two peaks visible in the Fourier space. The direction of the structural orientation was identified by a Fourier transform based algorithm [13]. To this end, the covariance matrix of the signal in Fourier space was calculated, and subjected to PCA analysis. For this purpose, a mask corresponding to the expected sarcomeric periodicity of 1.5-3.5 µm (windowing of the Fourier signal) was applied before PCA analysis was performed [42]. The volume was then rotated in such a way that the sarcomeric signal was aligned along a main axis. Figure 6(c) shows the rotated Fourier space. To increase the signal of the sarcomeric periodicity, the intensities in a range of 20 px from the main axis were integrated. The corresponding intensity profile is shown in Fig. 6(d). The two peaks correspond to an averaged sarcomeric periodicity of about 1.8 µm for the fixed tissue embedded in paraffin.
Fig. 6.
Reconstruction of the sarcomeric periodicity. (a) Reconstructed electron density of the biopsy taken from the paraffin-embedded heart. A maximum projection over 20 layers around a slice of a small cubic sub-volume with an edge length of 600 px. Scale bar: 25 µm. (b) Central slice of the 3d Fourier transform in the same direction as the slice shown in (a). Logscale, scale bar: 1.2 . (c) Zoom into the low spatial frequencies, after a rotation, which aligns the signal direction of the sarcomeric periodicity to the horizontal. Logscale, scale bar: 0.6 . (d) Fourier intensity profile along the direction of the sarcomeric signal, showing the side peaks corresponding to the sarcomeric periodicity. To reduce noise, the signal was integrated in the orthogonal direction in a range of 20 px, as indicated by the horizontal boundary lines in (c). The peaks appearing correspond to a real-space periodicity of 1.8 µm.
5. Outlook
In summary, we have demonstrated a multi-scale phase contrast tomography approach, which allows to image the structure of cardiac muscle starting from the scale of the the entire organ down to the sarcomere. To this end, we have implemented three levels of magnification and tomography configurations at the GINIX instrument of the PETRAIII storage ring, with correspondingly matched optics and detection. Importantly, phase retrieval by non-linear iterative reconstruction has allowed us to achieve high image quality for analysis of structural orientation in the whole heart as well as detailed views of the cyto-architecture down to sub-cellular features. As an outlook, we note that important improvements and extensions can be foreseen on various levels, including sample preparation, data analysis, instrumentation and optics.
Concerning sample preparation, further improvements could include fixation via perfusion to remove blood residuals. Air inclusions in the paraffin also often result in tomography artifacts and more efforts will be made to avoid formation of air bubbles or the removal thereof. Finally, better structure preservation of heart muscle can be expected without solvent exchange and paraffin embedding. We have already scanned hearts in PBS/Formalin. The challenge here is the much weaker contrast compared to dehydrated samples, see also [43], which requires higher propagation distance and careful optimization of photon energy.
Future extension of this work will be directed at bridging the gap between structure and function. Multi-scale phase contrast tomography of post mortem small animal hearts is already capable to provide 3d data, which can then be used as input for the simulation of cardiovascular functions. Modeling of signal excitation and transduction as well as mechanical functions require a quantitative understanding not only of tissue macrostructure, but also of (sub-)cellular orientation, as provided by the present approach. In particular, even the local sarcomere periodicity as well as the relative strength of the signal could be mapped by stitching high resolution tomograms.
Further, full-field tomography with continuous rotation, as shown here for the PB setup with tissue volume rates of µs, enables high throughput of samples, as required for biomedical studies with statistically sufficient number of diseased and control specimens. Small animal models for fibrosis and hypertension are currently under investigation, and show a very distinct pathologies of the 3d heart structure, which can complement conventional histological analysis.
Finally, it is of interest to briefly address the prospects for dynamic (time-resolved) propagation phase contrast tomography of a beating heart. Impressive instrumentation for a tomography and beamline compatible Langendorff perfusion system has been recently demonstrated at the TOMCAT beamline of the Swiss Light Source (SLS) by A. Bonnin and coworkers. Tremendous challenges are associated with this goal, not only in sufficiently fast data acquisition, reconstruction with a posteriori gating of projections, but also with keeping the dose at tolerable levels. To this end, we believe that full-field illumination with highly coherent undulator beams in the range of 25 keV-40 keV as will be provided by the next generation of (diffraction-limited) storage rings could provide a significant advantage for balancing contrast and dose, in combination with dose efficient single-photon counting detectors. However, this advantage can only be fully exploited if (i) undulator beams can be broadened by divergence behind a secondary focus, and (ii) if the effective pixel size can be sufficiently reduced by geometric magnification. To this end, the current work already shows how the cone beam illumination optics can improved significantly by filtering the beam in the secondary focal plane, keeping wavefront distortions at a tolerable level.
6. Supplementary
Fig. 7.
(a) Image of the detector and sample stage positioned about 5 m behind the focus of the KB-mirrors. b) Technical drawing of the tomography stage used for KB-illumination. The sample stage (yellow) including two compact linear piezo positioners for alignment of the axis of rotation, one rotation and a linear triaxial translation system for sample positioning, is placed on a kinematic mount of an aluminum plate which can manually be tilted by four adjusting screws in order to align the nick angle. The imaging system (Optique Peter with a PCO edge camera, black) was placed at distance behind the sample.
Fig. 8.
Processing of the data acquired with KB illumination. (a) The plane KB illumination profile with yields frequency artifacts emerging from the nanostructures of the mirrors. (b) By positioning a pinhole with a diameter of 3 µm in the focus of the beam, the profile of the illumination is smoothed. (c) An exemplary projection of murine heart embedded in paraffin. (d) The conventional empty beam corrected projection yield artifacts from small variations in the illumination profile. (e) By creating an artificial flat field using a principal component analysis approach these variations can be reduced. (f) The phase reconstruction was performed by the nonlinear-Tikhonov CTF approach.
Fig. 9.
(a) Illumination profile of the parallel beam. The colorbar of the intensity is scaled from 10 000 to 30 000 counts. (b) Exemplary flat field corrected projection of a ROI at the apex of the paraffin-embedded heart. Relative intensity: 0.4-0.75. (c) Phase reconstruction of the projection using the nonlinear-Tikhonov CTF. (d) Profile of the waveguide illumination. The colorbar of the intensity is given in logarithmic scale and set to 2 - 4.5. (e) Exemplary projection with a relative intensity of 0.2 - 0.9. (f) CTF reconstruction of the projection.
Acknowledgments
We thank Bärbel Heidrichs for help with sample preparation, Markus Osterhoff for integration of cameras and beamline control tools, Peter Luley for engineering support, and Michael Sprung and Fabian Westermeier for excellent working conditions at beamline P10.
Funding
Deutsche Forschungsgemeinschaft10.13039/501100001659 (EXC2067); Max-Planck-School Matter-to-Life.
Disclosures
The authors declare no conflicts of interest.
References
- 1.Anderson R. H., Smerup M., Sanchez-Quintana D., Loukas M., Lunkenheimer P. P., “The three-dimensional arrangement of the myocytes in the ventricular walls,” Clin. Anat. 22(1), 64–76 (2009). 10.1002/ca.20645 [DOI] [PubMed] [Google Scholar]
- 2.Jouk P.-S., Mourad A., Milisic V., Michalowicz G., Raoult A., Caillerie D., Usson Y., “Analysis of the fiber architecture of the heart by quantitative polarized light microscopy. accuracy, limitations and contribution to the study of the fiber architecture of the ventricles during fetal and neonatal life,” Eur. J. Cardio-Thoracic Surg. 31(5), 915–921 (2007). 10.1016/j.ejcts.2006.12.040 [DOI] [PubMed] [Google Scholar]
- 3.Torrent-Guasp F., Kocica M. J., Corno A. F., Komeda M., Carreras-Costa F., Flotats A., Cosin-Aguillar J., Wen H., “Towards new understanding of the heart structure and function,” Eur. J. Cardio-Thoracic Surg. 27(2), 191–201 (2005). 10.1016/j.ejcts.2004.11.026 [DOI] [PubMed] [Google Scholar]
- 4.Anderson R. H., Yanni J., Boyett M. R., Chandler N. J., Dobrzynski H., “The anatomy of the cardiac conduction system,” Clin. Anat. 22(1), 99–113 (2009). 10.1002/ca.20700 [DOI] [PubMed] [Google Scholar]
- 5.Bijnens B., Cikes M., Butakoff C., Sitges M., Crispi F., “Myocardial motion and deformation: What does it tell us and how does it relate to function?” Fetal Diagn. Ther. 32(1-2), 5–16 (2012). 10.1159/000335649 [DOI] [PubMed] [Google Scholar]
- 6.Mekkaoui C., Porayette P., Jackowski M. P., Kostis W. J., Dai G., Sanders S., Sosnovik D. E., “Diffusion MRI tractography of the developing human fetal heart,” PLoS One 8(8), e72795 (2013). 10.1371/journal.pone.0072795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Garcia-Canadilla P., Dejea H., Bonnin A., Balicevic V., Loncaric S., Zhang C., Butakoff C., Aguado-Sierra J., Vázquez M., Jackson L. H., Stuckey D. J., Rau C., Stampanoni M., Bijnens B., Cook A. C., “Complex congenital heart disease associated with disordered myocardial architecture in a midtrimester human fetus,” Circ. Cardiovasc. Imaging 11(10), e007753 (2018). 10.1161/CIRCIMAGING.118.007753 [DOI] [PubMed] [Google Scholar]
- 8.Gonzalez-Tendero A., Zhang C., Balicevic V., Cárdenes R., Loncaric S., Butakoff C., Paun B., Bonnin A., Garcia-Cañadilla P., Muñoz-Moreno E., Gratacós E., Crispi F., Bijnens B., “Whole heart detailed and quantitative anatomy, myofibre structure and vasculature from x-ray phase-contrast synchrotron radiation-based micro computed tomography,” Eur. Heart J. Cardiovasc. Imaging 18(7), 732–741 (2017). 10.1093/ehjci/jew314 [DOI] [PubMed] [Google Scholar]
- 9.Dejea H., Garcia-Canadilla P., Stampanoni M., Zamora M., Crispi F., Bijnens B., Bonnin A., Microstructural analysis of cardiac endomyocardial biopsies with synchrotron radiation-based x-ray phase contrast imaging, Functional Imaging and Modelling of the Heart (Springer International Publishing, 201723–31 [Google Scholar]
- 10.Mirea I., Varray F., Zhu Y. M., Fanton L., Langer M., Jouk P. S., Michalowicz G., Usson Y., Magnin I. E., Very high-resolution imaging of post-mortem human cardiac tissue using x-ray phase contrast tomography, Functional Imaging and Modeling of the Heart (Springer International Publishing, 2015172–179 [Google Scholar]
- 11.Kaneko Y., Shinohara G., Hoshino M., Morishita H., Morita K., Oshima Y., Takahashi M., Yagi N., Okita Y., Tsukube T., “Intact imaging of human heart structure using x-ray phase-contrast tomography,” Pediatric Cardiol. 38(2), 390–393 (2017). 10.1007/s00246-016-1527-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dejea H., Garcia-Canadilla P., Cook A. C., Guasch E., Zamora M., Crispi F., Stampanoni M., Bijnens B., Bonnin A., “Comprehensive analysis of animal models of cardiovascular disease using multiscale x-ray phase contrast tomography,” Sci. Rep. 9, 18278 (2019). 10.1038/s41598-019-54945-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Reichardt M., Töpperwien M., Khan A., Alves F., Salditt T., “Fiber orientation in a whole mouse heart reconstructed by laboratory phase-contrast micro-ct,” Proc. SPIE 11113, 111130S (2019). 10.1117/12.2527744 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Scheffel H., Alkadhi H., Plass A., Vachenauer R., Desbiolles L., Gaemperli O., Schepis T., Frauenfelder T., Schertler T., Husmann L., Grunenfelder J., Genoni M., Kaufmann P. A., Marincek B., Leschka S., “Accuracy of dual-source CT coronary angiography: first experience in a high pre-test probability population without heart rate control,” Eur. Radiol. 16(12), 2739–2747 (2006). 10.1007/s00330-006-0474-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Degenhardt K., Wright A. C., Horng D., Padmanabhan A., Epstein J. A., “Rapid 3d phenotyping of cardiovascular development in mouse embryos by micro-CT with iodine staining,” Circ. Cardiovasc. Imaging 3(3), 314–322 (2010). 10.1161/CIRCIMAGING.109.918482 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stephenson R. S., Boyett M. R., Hart G., Nikolaidou T., Cai X., Corno A. F., Alphonso N., Jeffery N., Jarvis J. C., “Contrast enhanced micro-computed tomography resolves the 3-dimensional morphology of the cardiac conduction system in mammalian hearts,” PLoS ONE 7 (2012). [DOI] [PMC free article] [PubMed]
- 17.Reichardt M., Frohn J., Toepperwien M., Nicolas J.-D., Markus A., Alves F., Salditt T., “Nanoscale holographic tomography of heart tissue with x-ray waveguide optics,” Proc. SPIE 10391, 1039105 (2017). 10.1117/12.2276648 [DOI] [Google Scholar]
- 18.Nicolas J.-D., Bernhardt M., Schlick S. F., Tiburcy M., Zimmermann W.-H., Khan A., Markus A., Alves F., Toischer K., Salditt T., “X-ray diffraction imaging of cardiac cells and tissue,” Prog. Biophys. Mol. Biol. 144, 151–165 (2019). 10.1016/j.pbiomolbio.2018.05.012 [DOI] [PubMed] [Google Scholar]
- 19.Nicolas J.-D., Bernhardt M., Markus A., Alves F., Burghammer M., Salditt T., “Scanning x-ray diffraction on cardiac tissue: automatized data analysis and processing,” J. Synchrotron Rad. 24(6), 1163–1172 (2017). 10.1107/S1600577517011936 [DOI] [PubMed] [Google Scholar]
- 20.Nicolas J.-D., Bernhardt M., Krenkel M., Richter C., Luther S., Salditt T., “Combined scanning X-ray diffraction and holographic imaging of cardiomyocytes,” J. Appl. Crystallogr. 50(2), 612–620 (2017). 10.1107/S1600576717003351 [DOI] [Google Scholar]
- 21.Bernhardt M., Nicolas J.-D., Osterhoff M., Mittelstädt H., Reuss M., Harke B., Wittmeier A., Sprung M., Köster S., Salditt T., “Correlative microscopy approach for biology using x-ray holography, x-ray scanning diffraction, and sted microscopy,” Nat. Commun. 9(1), 3641 (2018). 10.1038/s41467-018-05885-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Baličević V., Lončarić S., Cárdenes R., Gonzalez-Tendero A., Paun B., Crispi F., Butakoff C., Bijnens B., “Assessment of myofiber orientation in high resolution phase-contrast CT images,” in Functional Imaging and Modeling of the Heart, (Springer International Publishing, 2015), pp. 111–119. [Google Scholar]
- 23.Maretzke S., “A uniqueness result for propagation-based phase contrast imaging from a single measurement,” Inverse Prob. 31(6), 065003 (2015). 10.1088/0266-5611/31/6/065003 [DOI] [Google Scholar]
- 24.Hagemann J., Töpperwien M., Salditt T., “Phase retrieval for near-field X-ray imaging beyond linearisation or compact support,” Appl. Phys. Lett. 113(4), 041109 (2018). 10.1063/1.5029927 [DOI] [Google Scholar]
- 25.Paganin D., Mayo S. C., Gureyev T. E., Miller P. R., Wilkins S. W., “Simultaneous phase and amplitude extraction from a single defocused image of a homogeneous object,” J. Microsc. 206(1), 33–40 (2002). 10.1046/j.1365-2818.2002.01010.x [DOI] [PubMed] [Google Scholar]
- 26.Paganin D., Nugent K. A., “Noninterferometric Phase Imaging with Partially Coherent Light,” Phys. Rev. Lett. 80(12), 2586–2589 (1998). 10.1103/PhysRevLett.80.2586 [DOI] [Google Scholar]
- 27.Cloetens P., Ludwig W., Baruchel J., Van Dyck D., Van Landuyt J., Guigay J. P., Schlenker M., “Holotomography: Quantitative phase tomography with micrometer resolution using hard synchrotron radiation x rays,” Appl. Phys. Lett. 75(19), 2912–2914 (1999). 10.1063/1.125225 [DOI] [Google Scholar]
- 28.Salditt T., Osterhoff M., Krenkel M., Wilke R. N., Priebe M., Bartels M., Kalbfleisch S., Sprung M., “Compound focusing mirror and X-ray waveguide optics for coherent imaging and nano-diffraction,” J. Synchrotron Radiat. 22(4), 867–878 (2015). 10.1107/S1600577515007742 [DOI] [PubMed] [Google Scholar]
- 29.Bartels M., Krenkel M., Cloetens P., Möbius W., Salditt T., “Myelinated mouse nerves studied by x-ray phase contrast zoom tomography,” J. Struct. Biol. 192(3), 561–568 (2015). 10.1016/j.jsb.2015.11.001 [DOI] [PubMed] [Google Scholar]
- 30.Töpperwien M., Van der Meer F., Stadelmann C., Salditt T., “Three-dimensional virtual histology of human cerebellum by X-ray phase-contrast tomography,” Proc. Natl. Acad. Sci. U. S. A. 115(27), 6940–6945 (2018). 10.1073/pnas.1801678115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Homann C., Hohage T., Hagemann J., Robisch A.-L., Salditt T., “Validity of the empty-beam correction in near-field imaging,” Phys. Rev. A 91(1), 013821 (2015). 10.1103/PhysRevA.91.013821 [DOI] [Google Scholar]
- 32.Hagemann J., Robisch A.-L., Luke D. R., Homann C., Hohage T., Cloetens P., Suhonen H., Salditt T., “Reconstruction of wave front and object for inline holography from a set of detection planes,” Opt. Express 22(10), 11552–11569 (2014). 10.1364/OE.22.011552 [DOI] [PubMed] [Google Scholar]
- 33.Robisch A.-L., Wallentin J., Pacureanu A., Cloetens P., Salditt T., “Holographic imaging with a hard x-ray nanoprobe: ptychographic versus conventional phase retrieval,” Opt. Lett. 41(23), 5519–5522 (2016). 10.1364/OL.41.005519 [DOI] [PubMed] [Google Scholar]
- 34.Villanueva-Perez P., Arcadu F., Cloetens P., Stampanoni M., “Contrast-transfer-function phase retrieval based on compressed sensing,” Opt. Lett. 42(6), 1133–1136 (2017). 10.1364/OL.42.001133 [DOI] [PubMed] [Google Scholar]
- 35.Lohse L. M., Robisch A.-L., Töpperwien M., Maretzke S., Krenkel M., Hagemann J., Salditt T., “A phase retrieval toolbox for x-ray holography and tomography,” Journal of Synchrotron Radiation (2020). In press. [DOI] [PMC free article] [PubMed]
- 36.van Aarle W., Palenstijn W. J., Cant J., Janssens E., Bleichrodt F., Dabravolski A., De Beenhouwer J., Batenburg K. J., Sijbers J., “Fast and flexible X-ray tomography using the ASTRA toolbox,” Opt. Express 24(22), 25129–25147 (2016). 10.1364/OE.24.025129 [DOI] [PubMed] [Google Scholar]
- 37.Palenstijn W. J., Batenburg K. J., Sijbers J., “The astra tomography toolbox,” in 13th International Conference on Computational and Mathematical Methods in Science and Engineering. CMMSE, (2013). [Google Scholar]
- 38.Ketcham R. A., “New algorithms for ring artifact removal,” Proc. SPIE 6318, 63180O (2006). 10.1117/12.680939 [DOI] [Google Scholar]
- 39.Töpperwien M., Markus A., Alves F., Salditt T., “Contrast enhancement for visualizing neuronal cytoarchitecture by propagation-based x-ray phase-contrast tomography,” NeuroImage 199, 70–80 (2019). 10.1016/j.neuroimage.2019.05.043 [DOI] [PubMed] [Google Scholar]
- 40.Reichardt M., Töpperwien M., Khan A., Alves F., Salditt T., “Fiber orientation in a whole mouse heart reconstructed by laboratory phase-contrast micro-CT,” J. Med. Imag. 7(2), 1 (2020). 10.1117/1.JMI.7.2.023501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ayachit U., The ParaView Guide: A Parallel Visualization Application (Kitware Inc., 2015). [Google Scholar]
- 42.Irving T. C., Konhilas J., Perry D., Fischetti R., de Tombe P. P., “Myofilament lattice spacing as a function of sarcomere length in isolated rat myocardium,” Am. J. Physiol. Circ. Physiol. 279(5), H2568–H2573 (2000). 10.1152/ajpheart.2000.279.5.H2568 [DOI] [PubMed] [Google Scholar]
- 43.Patzelt M., Mrzilkova J., Dudak J., Krejci F., Zemlicka J., Karch J., Musil V., Rosina J., Sykora V., Horehledova B., Zach P., “Ethanol fixation method for heart and lung imaging in micro-CT,” Jpn. J. Radiol. 37(6), 500–510 (2019). 10.1007/s11604-019-00830-6 [DOI] [PubMed] [Google Scholar]