Large-Scale Exome Sequencing Study Implicates Both Developmental and Functional Changes in the Neurobiology of Autism

SUMMARY

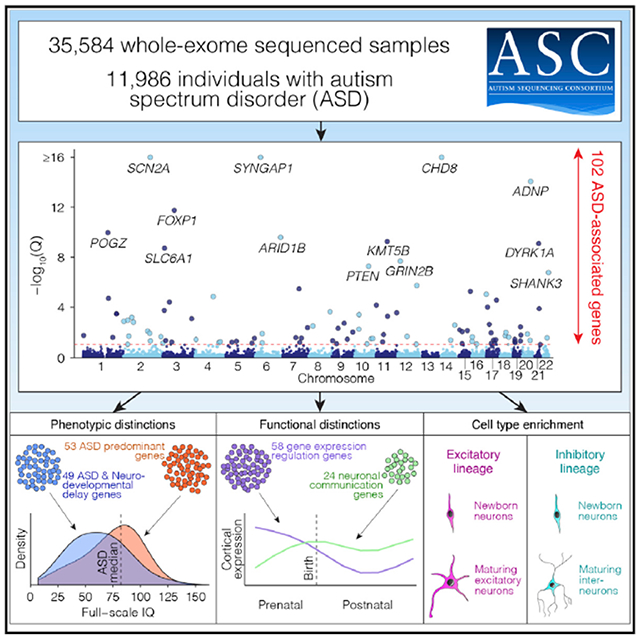
We present the largest exome sequencing study of autism spectrum disorder (ASD) to date (n = 35,584 total samples, 11,986 with ASD). Using an enhanced analytical framework to integrate de novo and case-control rare variation, we identify 102 risk genes at a false discovery rate of 0.1 or less. Of these genes, 49 show higher frequencies of disruptive de novo variants in individuals ascertained to have severe neurodevelopmental delay, whereas 53 show higher frequencies in individuals ascertained to have ASD; comparing ASD cases with mutations in these groups reveals phenotypic differences. Expressed early in brain development, most risk genes have roles in regulation of gene expression or neuronal communication (i.e., mutations effect neurodevelopmental and neurophysiological changes), and 13 fall within loci recurrently hit by copy number variants. In cells from the human cortex, expression of risk genes is enriched in excitatory and inhibitory neuronal lineages, consistent with multiple paths to an excitatory-inhibitory imbalance underlying ASD.

Graphical Abstract

In Brief

Large-scale sequencing of patients with autism allows identification of over 100 putative ASD-associated genes, the majority of which are neuronally expressed, and investigation of distinct genetic influences on ASD compared with other neurodevelopmental disorders.

INTRODUCTION

Rare inherited and de novo variants are major contributors to individual risk for autism spectrum disorder (ASD) (De Rubeis et al., 2014; Iossifov et al., 2014; Sanders et al., 2015). When such rare variation disrupts a gene in individuals with ASD more often than expected by chance, it implicates that gene in risk (He et al., 2013). These risk genes provide insight into the underpinnings of ASD both individually (Ben-Shalom et al., 2017; Bernier et al., 2014) and en masse (De Rubeis et al., 2014; Ruzzo et al., 2019; Sanders et al., 2015; Willsey et al., 2013). However, fundamental questions about the altered neurodevelopment and altered neurophysiology in ASD—including when it occurs, where, and in what cell types—remain poorly resolved.

Here we present the largest exome sequencing study in ASD to date. We assembled a cohort of 35,584 samples, including 11,986 with ASD. We introduce an enhanced Bayesian analytic framework that incorporates recently developed gene- and variant-level scores of evolutionary constraint of genetic variation, and we use it to identify 102 ASD-associated genes (false discovery rate [FDR] ≤ 0.1). Because ASD is often one of a constellation of symptoms of neurodevelopmental delay (NDD), we identify subsets of the 102 ASD-associated genes that have disruptive de novo variants more often in NDD-ascertained or ASD-ascertained cohorts. We also consider the cellular function of ASD-associated genes and, by examining extant data from single cells in the developing human cortex, (1) show that their expression is enriched in maturing and mature excitatory and inhibitory neurons from midfet al development onward, (2) confirm their role in neuronal communication or regulation of gene expression, and (3) show that these functions are separable. Together, these insights form an important step forward in elucidating the neurobiology of ASD.

RESULTS

Dataset

We analyzed whole-exome sequence (WES) data from 35,584 samples that passed our quality control procedures (STAR Methods): 21,219 family-based samples (6,430 ASD cases, 2,179 unaffected siblings, and both parents) and 14,365 case-control samples (5,556 ASD cases, 8,809 controls) (Figure S1; Table S1). Of these, 6,197 samples were newly sequenced by our consortium (1,908 cases with parents, 274 additional cases, 25 controls) and 11,265 samples were newly incorporated (416 cases with parents, plus 4,811 additional cases and 5,214 controls from the Danish iPSYCH study; Satterstrom et al., 2018).

From the family-based data, we identified 9,345 rare de novo variants in protein-coding exons (allele frequency ≤ 0.1% in our dataset and non-psychiatric subsets of reference databases): 63% of cases and 59% of unaffected siblings carried at least one such variant (4,073 of 6,430 and 1,294 of 2,179, respectively; Table S1; Figure S1). For inherited and case-control analyses, we included variants with an allele count of no more than five in our dataset or a reference database (STAR Methods; Kosmicki et al., 2017; Leket al., 2016).

Effect of Genetic Variants on ASD Risk

Because protein-truncating variants (PTVs; nonsense, frameshift, and essential splice site variants) show a greater difference in burden between ASD cases and controls than missense variants, their average effect on liability must be larger (He et al., 2013). Measures of functional severity assessing evolutionary constraint against deleterious genetic variation, such as the “probability of loss-of-function intolerance” (pLI) score (Kosmicki et al., 2017; Lek et al., 2016) and the integrated ‘‘missense badness, PolyPhen-2, constraint” (MPC) score (Samocha et al., 2017), can further delineate variant classes with higher burden. Therefore, we divided the list of rare autosomal genetic variants into seven tiers of predicted functional severity: three tiers for PTVs by pLI score (≥0.995, 0.5–0.995, 0–0.5) in order of decreasing expected effect; likewise, three tiers for missense variants by MPC score (≥2, 1–2, 0–1); and a single tier for synonymous variants, expected to have minimal effect. We further divided variants by their inheritance pattern: de novo, inherited, and case-control. Because ASD is associated with reduced fecundity (Power et al., 2013), variation associated with it is subject to natural selection. Inherited variation has survived at least one generation of viability and fecundity selection in the parental generation whereas de novo variation in offspring has not. Thus, on average, de novo mutations are exposed to less selective pressure and could mediate substantial risk for ASD. This expectation is borne out by the substantially higher proportions of all three PTV tiers and the two most severe missense variant tiers in de novo compared with inherited variants (Figure 1A).

Figure 1. Distribution of Rare Autosomal Protein-Coding Variants in ASD Cases and Controls.

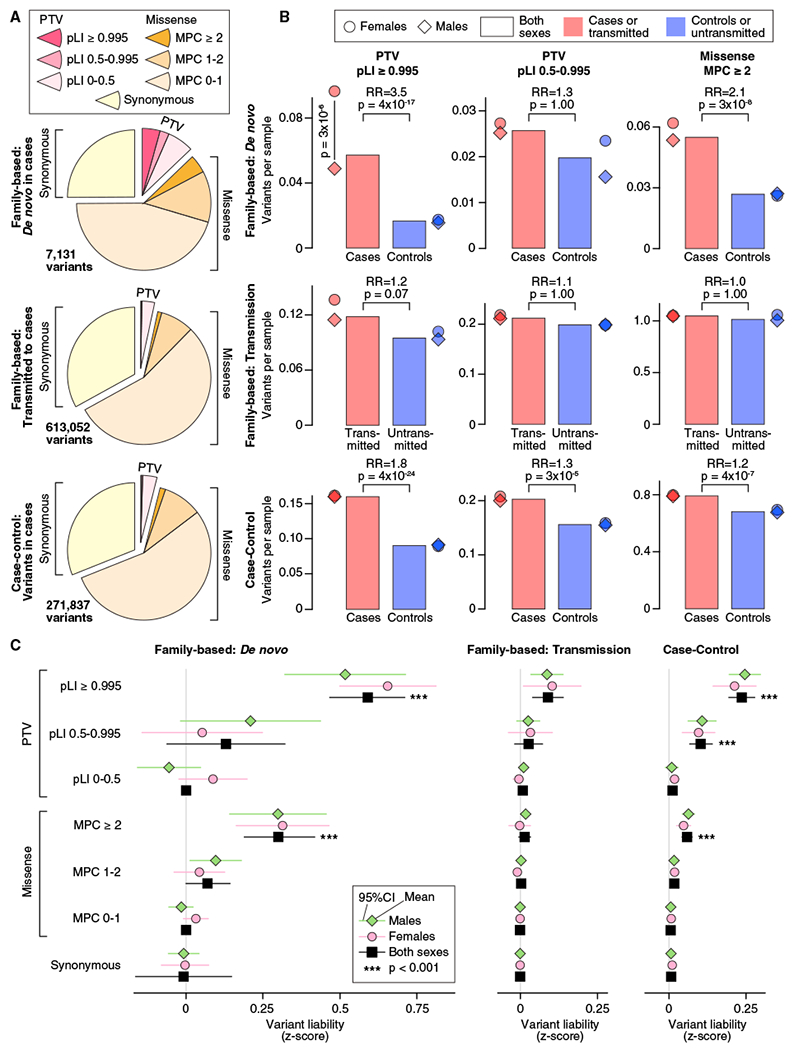
(A) The proportion of rare autosomal genetic variants split by predicted functional consequences, represented by color, is displayed for family-based (split into de novo and inherited variants) and case-control data. PTVs and missense variants are split into three tiers of predicted functional severity, represented by shade, based on the pLI and MPC metrics, respectively.

(B) The relative difference in variant frequency (i.e., burden) between ASD cases and controls (top and bottom) or transmitted and untransmitted parental variants (center) is shown for the top two tiers of functional severity for PTVs (left and center) and the top tier of functional severity for missense variants (right). Next to the bar plot, the same data are shown divided by sex.

(C) The relative difference in variant frequency shown in (B) is converted to a trait liability Z score, split by the same subsets used in (A). For context, a Z score of 2.18 would shift an individual from the population mean to the top 1.69% of the population (equivalent to an ASD threshold based on 1 in 68 children; Christensen et al., 2016). No significant difference in liability was observed between males and females for any analysis.

Statistical tests: (B) and (C), binomial exact test (BET) for most contrasts; exceptions were “both” and “case-control,” for which Fisher’s method for combining BET p values for each sex and, for case-control, each population was used; p values corrected for 168 tests are shown.

Comparing family-based cases with unaffected siblings in the 1,447 genes with pLI ≥ 0.995, there is a 3.5-fold enrichment of de novo PTVs (366 in 6,430 cases versus 35 in 2,179 controls; 0.057 versus 0.016 variants per sample (vps); p = 4 × 10⁻¹⁷, two-sided Poisson exact test; Figure 1B) and 1.2-fold enrichment of rare inherited PTVs (695 transmitted versus 557 untransmitted in 5,869 parents; 0.12 versus 0.10 vps; p = 0.07, binomial exact test; Figure 1B). The same genes in the case-control data show an intermediate 1.8-fold enrichment of PTVs (874 in 5,556 cases versus 759 in 8,809 controls; 0.16 versus 0.09 vps; p = 4 × 10⁻²⁴, binomial exact test; Figure 1B). Analysis of the middle tier of PTVs (0.5 ≤ pLI < 0.995) shows a similar but muted pattern (Figure 1B), whereas the lowest tier of PTVs (pLI < 0.5) shows no enrichment (Table S1).

De novo missense variants occur more frequently than de novo PTVs. Collectively, they show only marginal enrichment over the rate expected by chance (De Rubeis et al., 2014; Figure 1). The most severe de novo missense variants (MPC ≥ 2), however, show a frequency similar to the most severe tier of de novo PTVs. They yield 2.1-fold case enrichment (354 in 6,430 cases versus 58 in 2,179 controls; 0.055 versus 0.027 vps; p = 3 × 10⁻⁸, two-sided Poisson exact test; Figure 1B) with consistent 1.2-fold enrichment in case-control data (4,277 in 5,556 cases versus 6,149 in 8,809 controls; 0.80 versus 0.68 vps; p = 4 × 10⁻⁷, binomial exact test; Figure 1B). These variants show stronger enrichment than the middle tier of PTVs, whereas the other two tiers of missense variation are not significantly enriched (Table S1).

From our data, the proportion of the variance explained by de novo PTVs is 1.3%, 1.2% of it from the highest pLI category. The proportion of the variance explained by de novo MPC ≥ 2 missense variants is 0.5%, whereas all remaining missense variation explains 0.12%. Thus, in total, all exome de novo variants in the autosomes explain 1.92% of the variance of ASD.

Sex Differences in ASD Risk

ASD is more prevalent in males than females. In line with previous observations (De Rubeis et al., 2014), we observe a 2-fold enrichment of de novo PTVs in highly constrained genes in affected females (n = 1,097) versus affected males (n = 5,333) (p = 3 × 10⁻⁶, two-sided Poisson exact test; Figure 1B; Table S1). This result is consistent with the female protective effect model, which postulates that females require an increased genetic load to reach the threshold for ASD diagnosis (Werling, 2016). The converse hypothesis is that risk variation has larger effects in males than infemales so that females require a higher burden to reach the same diagnostic threshold as males. Across all classes of genetic variants, we observed no significant sex differences in trait liability, consistent with the female protective effect model (Figure 1C; STAR Methods). Thus, we estimated the liability Z scores for different classes of variants from both sexes together (Figure 1C; Table S1) and leveraged them to enhance gene discovery.

ASD Gene Discovery

In previous risk gene discovery efforts, we used the transmitted and de novo association (TADA) model (He et al., 2013) to integrate protein-truncating and missense variants that are de novo, inherited, or from case-control populations and to stratify autosomal genes by FDR for association. Here we update the TADA model to include pLI score as a continuous metric for PTVs and MPC score as a two-tiered metric (≥2, 1–2) for missense variants (STAR Methods; Figure S2). From family data, we include de novo PTVs as well as de novo missense variants, whereas from the case-control, we include only PTVs; we do not include inherited variants because of the limited liabilities observed (Figure 1C). Our analyses reveal that these modifications result in an enhanced TADA model with greater sensitivity and accuracy than the original model (Figure 2A); no other covariates examined were important after accounting for these factors (STAR Methods).

Figure 2. Gene Discovery in the ASC Cohort.

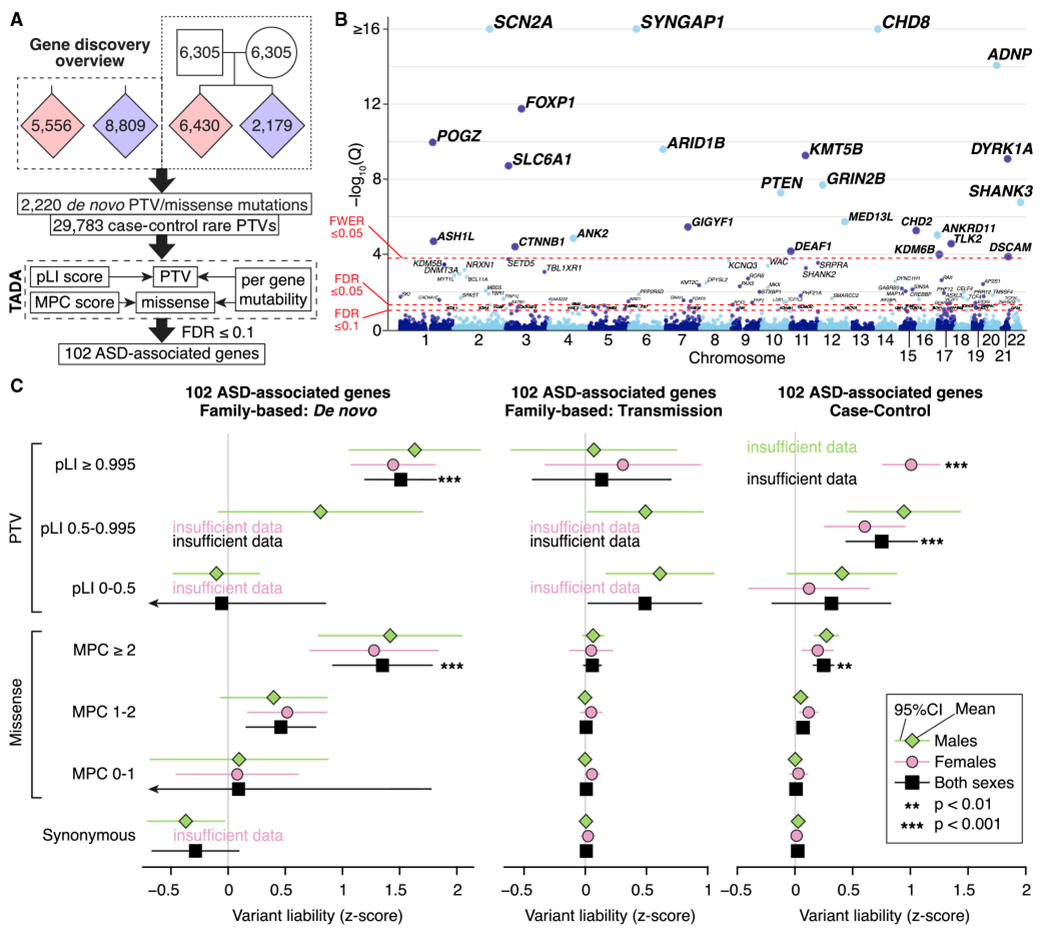
(A) WES data from 35,584 samples are entered into a Bayesian analysis framework (TADA) that incorporates pLI score for PTVs and MPC score for missense variants.

(B) The model identifies 102 autosomal genes associated with ASD at a false discovery rate (FDR) threshold of 0.1 or less, which is shown on the y axis of this Manhattan plot, with each point representing a gene. Of these, 78 pass the threshold FDR of 0.05 or less, and 26 pass the threshold family-wise error rate (FWER) of 0.05 or less.

(C) Repeating our ASD trait liability analysis (Figure 1C) for variants observed within the 102 ASD-associated genes only.

Statistical tests: (B), TADA; (C), BET for most contrasts; exceptions were “both” and “case-control,” for which Fisher’s method for combining BET p values for each sex and, for case-control, each population was used; p values corrected for 168 tests are shown.

Our refined TADA model identifies 102 ASD risk genes at FDR ≤ 0.1, of which 78 pass FDR ≤ 0.05 and 26 pass Bonferroni-corrected (p ≤ 0.05) thresholds (Figure 2B; Table S2). Simulation experiments (STAR Methods) show that the FDR is properly calibrated and relatively insensitive to estimates of the total number of ASD-related genes in the genome (Figure S2). Of the 102 ASD-associated genes, 60 were not discovered by our earlier analyses (De Rubeis et al., 2014; Iossifov et al., 2014; Sanders et al., 2015). These include 30 considered truly novel because they have not been implicated in autosomal dominant neurodevelopmental disorders (ASD, developmental delay, epilepsy, and intellectual disability) and were not significantly enriched for de novo and/or rare variants in previous studies (Table S2). The patterns of liability seen for the 102 genes are similar to that seen over all genes (compare Figure 2C with Figure 1C), although the effects of variants are uniformly larger, as would be expected for this selected list.

We did not analyze de novo mutations on chromosome X because they are rare, which reduces power for gene discovery from these data; the majority of de novo mutations are of paternal origin, and only females–who represent a minority of ASD diagnoses–receive an X chromosome from their fathers. Moreover, many of the known ASD genes identified on chromosome X show recessive-like inheritance, in which males inherit risk variation from an unaffected mother, and, with our current sample size, we are underpowered for inherited variation. Complementing these observations, when we assessed variants from chromosome X using sex-stratified case-control analyses, no gene had a significant excess of PTV and MPC ≥ 2 variants after Bonferroni correction (Table S2). Five genes did show evidence of increased de novo variants (ARHGEF9, IQSEC2, SLC25A6, PCDH19, and OFD1); all but SLC25A6 are already implicated in X-linked intellectual disability. Of these variants, 43% are in females (which make up 17% of the cohort), underscoring the challenges of analyzing de novo mutations on chromosome X.

Patterns of Mutations in ASD Genes

The ratio of PTVs to missense mutations varies substantially between genes (Figure 3A). Some genes reach our association threshold through PTVs alone (e.g., ADNP), and three genes have a significant excess of PTVs relative to missense mutations, accounting for gene mutability: SYNGAP1, DYRK1A, and ARID1B (p < 0.0005, binomial test). Because of the increased cohort size and availability of the MPC metric, we are also able, for the first time, to associate genes with ASD based primarily on de novo missense variation. Four genes carry four or more de novo missense variants (MPC ≥ 1) in ASD cases and one or no PTVs: DEAF1, KCNQ3, SCN1A, and SLC6A1 (Figure 3A; Table S3).

Figure 3. Genetic Characterization of ASD Genes.

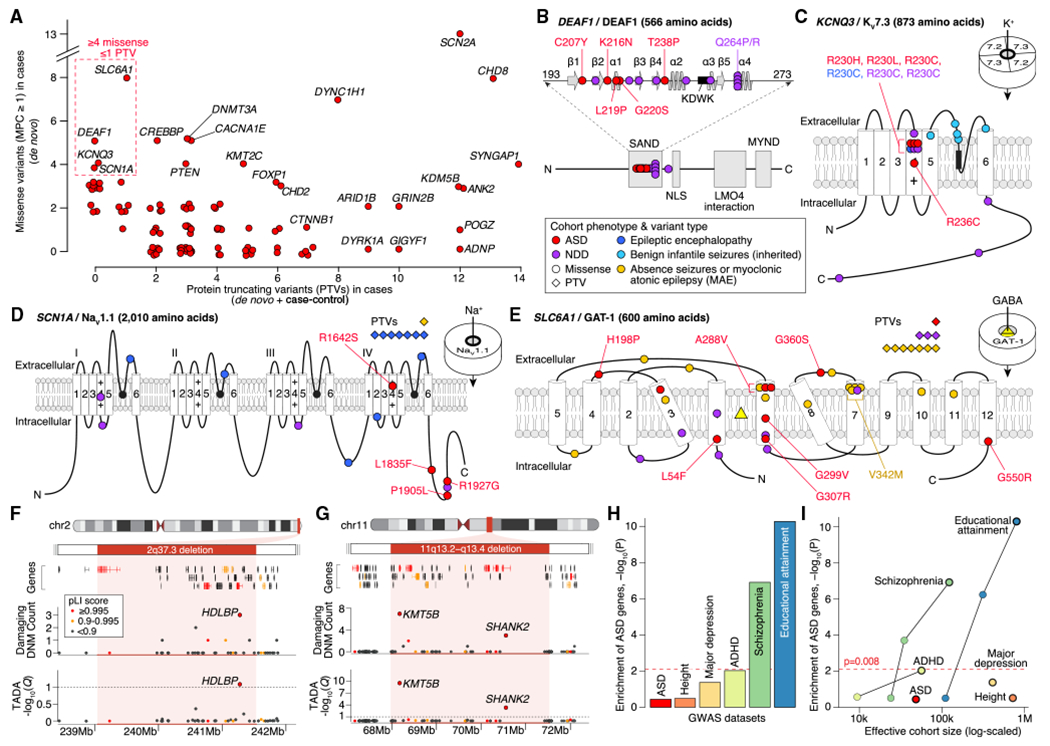
(A) Count of PTVs versus missensevariants(MPC ≥ 1) in cases for each ASD-associated gene (red points, selected genes labeled). These counts reflect the data used by TADA for association analysis: de novo and case-control data for PTVs; de novo only for missense.

(B) Location of ASD de novo missense variants in DEAF1. The five ASD variants (marked in red) are in the SAND (Sp100, AIRE-1, NucP41/75, DEAF-1) DNA-binding domain (amino acids 193–273, spirals show α helices, arrows show β sheets, KDWK isthe DNA-binding motif) alongside 10 variants observed in NDD, several of which have been shown to reduce DNA binding, including Q264P and Q264R (Chen et al., 2017; Heyne et al., 2018; Vultovan Silfhout et al., 2014).

(C) Location of ASD missensevariants in KCNQ3. All four ASD variants are located in the voltage sensor (fourth of six transmembrane domains), with three in the same residue (R230), including the gain-of-function R230C mutation observed in NDD (Heyne et al., 2018; Miceli et al, 2015). Five inherited variants observed in benign infantile seizures are shown in the pore loop (Landrum et al., 2014; Maljevic et al., 2016).

(D) Location of ASD missense variants in SCN1A along side 17 de novo variants in NDD and epilepsy (Heyne et al., 2018).

(E) Location of ASD missense variants in SLC6A1 along side 31 de novo variants in NDD and epilepsy (Heyne et al., 2018; Johannesen et al., 2018).

(F) Subtelomeric 2q37 deletions are associated with facial dysmorphisms, brachydactyly, high BMI, NDD, and ASD (Leroy et al., 2013). Although three genes within the locus have a pLI score of 0.995 or higher, only HDLBP is associated with ASD.

(G) Deletions atthe 11q13.2–q13.4 locus have been observed in NDD, ASD, and otodental dysplasia (Coe et al., 2014; Cooperet al., 2011). Five genes within the locus have a pLI score of 0.995 or higher, including two ASD genes: KMT5B and SHANK2.

(H) Assessment of gene-based enrichment, via MAGMA, of 102 ASD genes against genome-wide significant common variants from six GWASs.

(I) Gene-based enrichment of 102 ASD genes in multiple GWASs as a function of effective cohort size. The GWAS used for each disorder in (I) has a black outline.

Statistical tests: (F) and (G), TADA; (H) and (I), MAGMA.

For DEAF1, five de novo missense variants were observed, and all reside in the SAND (Sp100, AIRE-1, NucP41/75, DEAF-1) domain (Figure 3B), which is critical for dimerization and DNA binding (Bottomley et al., 2001; Jensik et al., 2004). For KCNQ3, all four de novo missense variants modify arginine residues in the voltage-sensing fourth transmembrane domain, with three at a single residue previously characterized as gain of function in NDD (R230C; Figure 3C; Miceli et al., 2015). Of the four de novo missense variants identified in SCN1A (Figure 3A; Table S3), three occur in the C terminus (Figure 3D), and all four carriers have seizures. Finally, we observe eight de novo missense variants in SLC6A1 (Figure 3E), with four in the sixth transmembrane domain and one recurring in two independent cases (A288V). Five of the six subjects with available information on history of seizure have seizures; all four subjects assessed have intellectual disability.

ASD Genes within Recurrent Copy Number Variants (CNVs)

Large CNVs represent another important source of risk for ASD (Sebat et al., 2007), but these genomic disorder segments can include dozens of genes, complicating the identification of driver gene(s) within these regions. To determine whether the 102 ASD genes could nominate driver genes within genomic disorder regions, we first curated a consensus list from nine sources, totaling 823 protein-coding genes in 51 autosomal genomic disorder loci associated with ASD or ASD-related phenotypes, including NDD (Table S3). Of the51 loci, 12 encompassed a total of 13 ASD-associated genes (Table S3), which is greater than expected by chance when controlling for number of genes, PTV mutation rate, and brain expression levels per gene (2.3-fold increase; p = 2.3 × 10⁻³, permutation). These 12 loci were divided into three groups: (1) the overlapping ASD gene matched the consensus driver gene (e.g., SHANK3 for Phelan-McDermid syndrome; Soorya et al., 2013); (2) an ASD gene emerged that did not match the previously predicted driver gene(s) within the region, such as HDLBP at 2q37.3 (Figure 3F), where HDAC4 has been hypothesized as a driver gene (Williams et al., 2010); and (3) no previous driver gene had been established within the locus, such as BCL11A at 2p15-p16.1. One locus, 11q13.2-q13.4, had two of our 102 genes (SHANK2 and KMT5B; Figure 3G), highlighting that genomic disorder loci can result from risk conferred by multiple genes, potentially including genes with small effect sizes that we are underpowered to detect.

Relationship of ASD Genes with GWAS Signals

Common variation plays an important role in ASD risk (Gaugler et al., 2014), and recent genome-wide association studies (GWASs) reveal a handful of ASD-associated loci (Grove et al., 2019). Notably, among the five GWAS-significant ASD hits (Grove et al., 2019), KMT2E is implicated by both GWAS and the list of 102 FDR ≤ 0.1 genes described here (Fisher’s exact test, p = 0.029). Thus, using MAGMA (multi-marker analysis of genomic annotation; de Leeuw et al., 2015), we asked whether common genetic variation in or near the 102 identified genes (within 10 kb) influences ASD risk or other related traits. For these associated genes, MAGMA integrates GWAS summary statistics to determine whether their signal is enriched over background; namely, brain-expressed protein-coding genes. We used results from six GWAS datasets: ASD, schizophrenia, major depressive disorder, and attention deficit hyperactivity disorder (ADHD), which are all positively genetically correlated with ASD and with each other; educational attainment, which is positively correlated with ASD and negatively correlated with schizophrenia and ADHD; and human height as a negative control (Table S3; Demontis et al., 2019; Grove et al., 2019; Lee et al., 2018; Neale et al., 2010; Okbay et al., 2016; Rietveld et al., 2013; Ripke et al., 2011,2013a, 2013b; Schizophrenia Working Group of the Psychiatric Genomics Consortium, 2014; Wray et al., 2018; Yengo et al., 2018; Zheng et al., 2017) . Correcting for six analyses, only the schizophrenia and educational attainment GWAS signals show significant enrichment in ASD genes (Figure 3H). The ASD GWAS signal was not enriched, potentially because common and rare variation contributing to ASD risk affect distinct genes or potentially because we currently lack the sample sizes to detect the convergence of the two. We conjecture that the second hypothesis is more likely because of three results: the known genetic correlation of schizophrenia and educational attainment with ASD, the enrichment of common variation conferring risk for both found in the 102 ASD genes, and the statistically significant overlap we demonstrate for KMT2E. In addition, effective cohort sizes for schizophrenia, educational attainment, and height dwarf that for ASD (Figure 3I), and the quality of the GWAS signal strongly increases with sample size. Thus, for results from well-powered GWASs, it is reassuring that there is no signal for height but a clearly detectable signal for two traits genetically correlated with ASD.

Relationship between ASD and Other Neurodevelopmental Disorders

Family studies yield high heritability estimates in ASD (Yip et al., 2018) , whereas estimates of heritability in severe NDD are lower (Reichenberg et al., 2016). Consistent with these observations, exome studies identify a higher frequency of disruptive de novo variants in severe NDD than in ASD (Deciphering Developmental Disorders Study, 2017). Because 30%–50% of ASD individuals have comorbid intellectual disability and/or NDD, many genes are associated with both disorders (Pinto et al., 2010). Distinguishing genes that, when disrupted, lead to ASD more frequently than NDD could shed new light on how atypical neurodevelopment maps onto the core deficits of ASD.

To partition the 102 ASD genes in this manner, we compiled data from 5,264 trios ascertained for severe NDD (Table S4) and compared the relative frequency, R, of disruptive de novo variants (which we define as PTVs or missense variants with MPC ≥ 1) in ASD- or NDD-ascertained trios. Genes with R > 1 were classified as ASD-predominant (ASD_P, 50 genes), whereas those with R < 1 were classified as ASD with NDD (ASD_NDD, 49 genes). Based on case-control data, the three other genes were assigned to the ASD_P group (Figure 4A). Thirteen of the genes demonstrate nominally significant heterogeneity between samples ascertained for ASD versus NDD (Fisher’s exact test, p < 0.05) with only ANKRD11 and ASXL3 significant after correction for 102 genes; these and other heterogeneity analyses are described in STAR Methods and Table S4.

Figure 4. Phenotypic and Functional Categories of ASD-Associated Genes.

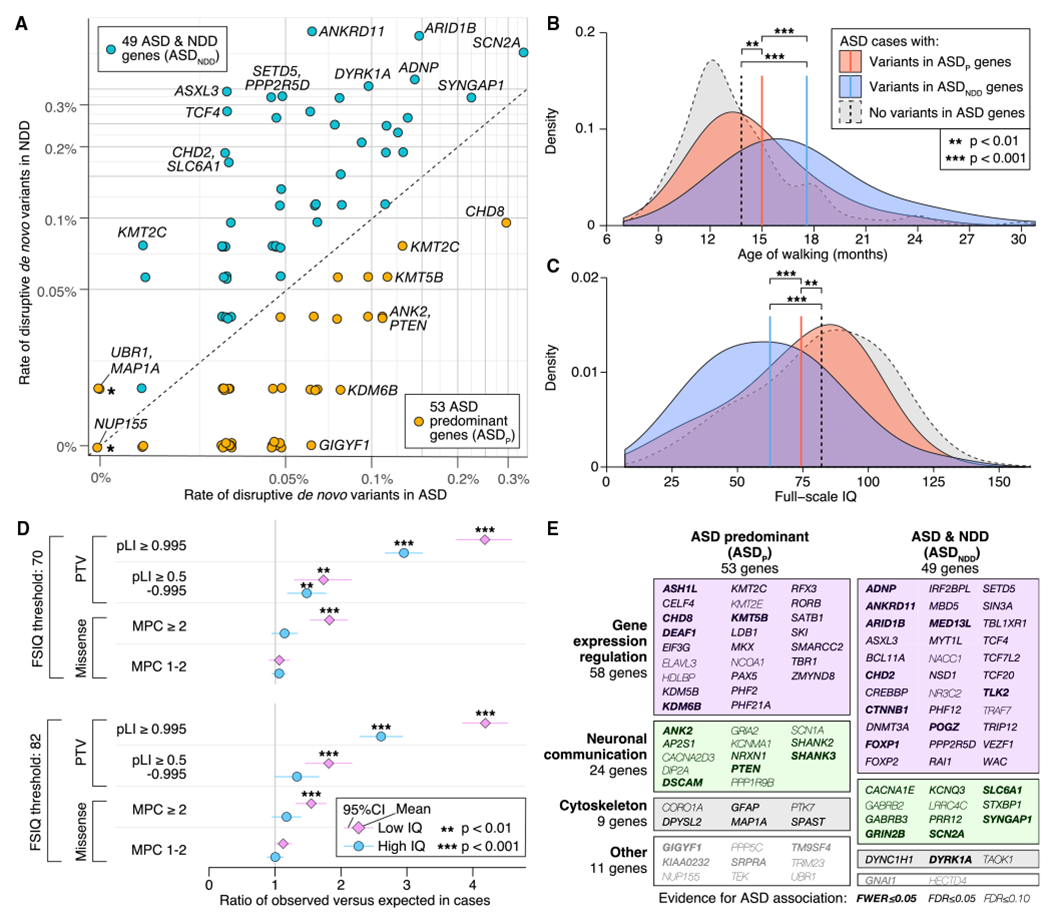
(A) Frequency of disruptive de novo variants (e.g., PTVs or missense variants with MPC ≥ 1) in ASD-ascertained and NDD-ascertained cohorts (Table S4) is shown for the 102 ASD-associated genes (selected genes labeled). Fifty genes with a higher frequency in ASD are designated ASD-predominant (ASDp), whereas the 49 genes more frequently mutated in NDD are designated as ASD_NDD. Three genes marked with a star(UBR1, MAP1A, and NUP155) are included in the ASDP category on the basis of case-control data (Table S4), which are not shown here. Of the 26 FWER genes, 10 are ASDp and 16 are ASD_NDD. Of the 102 genes, 13 demonstrate nominally significant heterogeneity between samples ascertained for ASD versus NDD (Table S4).

(B) ASD cases with disruptive de novo variants in ASD genes show delayed walking compared with ASD cases without such de novo variants, and the effect is greater for those with disruptive de novo variants in ASDNDD genes.

(C) Similarly, cases with disruptive de novo variants in ASD_NDD genes and, to a lesser extent, ASD_P genes have a lower full-scale IQ (FSIQ) than other ASD cases.

(D) Despite the association between de novo variants in ASD genes and cognitive impairment shown in (C), an excess of disruptive de novo variants is observed in cases without intellectual disability (FSIQ ≥ 70) or with an IQ above the cohort mean (FSIQ ≥ 82).

(E) Along with the phenotypic division (A), genes can also be classified functionally into four groups (gene expression regulation [GER], neuronal communication [NC], cytoskeleton, and other) based on Gene Ontology and research literature. The 102 ASD risk genes are shown in a mosaic plot divided by gene function and, from (A), the ASD versus NDD variant frequency, with the area of each box proportional to the number of genes.

Statistical tests: (B) and (C), t test; (D), chi-square test with 1° of freedom.

For ASD_P genes and transmission of rare PTVs (relative frequency < 0.001) from parents to their affected offspring, 44 PTVs were transmitted and 18 were not (p = 0.001, transmission disequilibrium test [TDT]), whereas, for ASD_NDD genes, 14 were transmitted and 8 were not (p = 0.29; TDT). The frequency of PTVs in parents is significantly greater in ASD_P genes (1.17 per gene) than in ASD_NDD genes (0.45 per gene; p = 6.6 × 10⁻⁶, binomial test), whereas the frequency of de novo PTVs in cases is not markedly different between the two groups (95 in ASD_P genes, 121 in ASD_NDD genes; p = 0.07, binomial test with probability of success = 0.503 [PTV in ASD_P genes]). The paucity of inherited PTVs in ASD_NDD genes is consistent with greater selective pressure acting against disruptive variants in these genes and highlights fundamental differences between these two classes.

In addition, ASD subjects who carry disruptive de novo variants in ASD_NDD genes walk 2.6 ± 1.2 months later (Figure 4B; p = 2.3 × 10⁻⁵, t test, df = 251) and have an IQ 11.9 ± 6.0 points lower (Figure 4C; p = 1.1 × 10⁻⁴, two-sided t test, df = 278), on average, than ASD subjects with disruptive de novo variants in ASD_P genes (Table S4). Both sets of subjects differ significantly from the rest of the cohort with respect to IQ and age of walking (Figures 4B and 4C; Table S4).

The data thus support an overall distinction between ASD_P and ASD_NDD genes en masse, although it is a matter of degree; disruptive de novo variants in both categories affect IQ and age of walking. Moreover, the smaller average effect of mutations on cognitive function in ASD_P genes relative to ASD_NDD genes does not mean that any individual carrying a disruptive de novo variant in an ASD_P gene necessarily has an IQ of 70 or higher; likewise, not all individuals carrying a disruptive de novo variant in an ASD_NDD gene have an IQ of less than 70. In addition, de novo variation plays an important role in ASD risk for both IQ groups. If we partition ASD cases into those with an IQ of 70 or higher (69.4%) versus those with an IQ of less than 70 (30.6%), individuals in the higher-IQ group still carry a greater burden of de novo variants relative to expectation, and this remains true when partitioning the IQ at the cohort mean (full-scale IQ[FSIQ] ≥ 82; Figure 4D; 3,010 of 6,430 have FSIQ information) or when considering the 102 ASD genes only (STAR Methods). Thus, excess burden is not limited to low-IQ cases, supporting the idea that de novo variants do not solely impair cognition (Robinson et al., 2014).

Functional Dissection of ASD Genes

Past analyses have identified two major functional groups of ASD genes: those involved in gene expression regulation (GER), including chromatin regulators and transcription factors, and those involved in neuronal communication (NC), including synaptic function (De Rubeis et al., 2014). Similarly, Gene Ontology enrichment analysis with the 102 ASD genes identifies 16 genes in the “regulation of transcription from RNA polymerase II promoter” category (GO:0006357, 5.7-fold enrichment, FDR = 6.2 × 10⁻⁶) and 9 in the “synaptic transmission” category (GO:0007268, 5.0-fold enrichment, FDR = 3.8 × 10⁻³). For further analyses, we used a combination of Gene Ontology and primary literature to assign genes to GER (n = 58), NC (n = 24), “cytoskeleton organization” (n = 9, GO:0007010), or “other” categories (STAR Methods; Table S4; Figure 4E). Interestingly, ASD subjects who carry disruptive de novo variants in either GER or NC genes showed delayed age of walking and reduced IQ compared with those with no mutations in the 102 genes (Figure S3; STAR Methods), yet carriers of disruptive variants in GER genes show significantly greater delays in age of walking compared with those with disruptive variants in NC genes.

ASD Genes Are Expressed Early in Brain Development

The 102 ASD genes can be subdivided by phenotypic effect (53 ASD_P genes, 49 ASD_NDD genes) and functional role (58 GER genes, 24 NC genes) to give five gene sets (including all 102). We first evaluated enrichment of these five gene sets in the 53 tissues with bulk RNA sequencing (RNA-seq) data in the Genotype-Tissue Expression (GTEx) resource (Battle et al., 2017). To enhance tissue-specific resolution, we selected genes that were expressed in one tissue at a significantly higher level than the remaining 52 tissues; specifically, log2 fold change of 0.5 or more and FDR of less than 0.05 (t test). Subsequently, we assessed over-representation of each ASD gene set within each of the 53 tissue-specific gene sets relative to a background of all other tissue-specific gene sets. Correcting for 53 tests, enrichment was observed in 11 of 13 brain regions, with the strongest enrichment in the cortex (30 genes, p = 3 × 10⁻⁶, odds ratio [OR] = 3.7; Figure 5A) and cerebellar hemisphere (48 genes, p = 3 × 10⁻⁶, OR = 2.9; Figure 5A). Of the four gene subsets, NC genes were the most highly enriched in the cortex (17 of 23, p = 3 × 10⁻¹¹, OR = 25; Figure 5A), whereas GER genes were the least enriched (10 of 58, p = 0.36, OR = 1.5; Figure 5A; Table S5). Notably, of the 102 ASD genes, only the cerebellar transcription factor PAX5 (FDR = 0.005, TADA) was not expressed in the cortex (78 expected; p = 1 × 10⁻⁹, binomial test).

Figure 5. Analysis of 102 ASD-Associated Genes in the Context of Gene Expression Data.

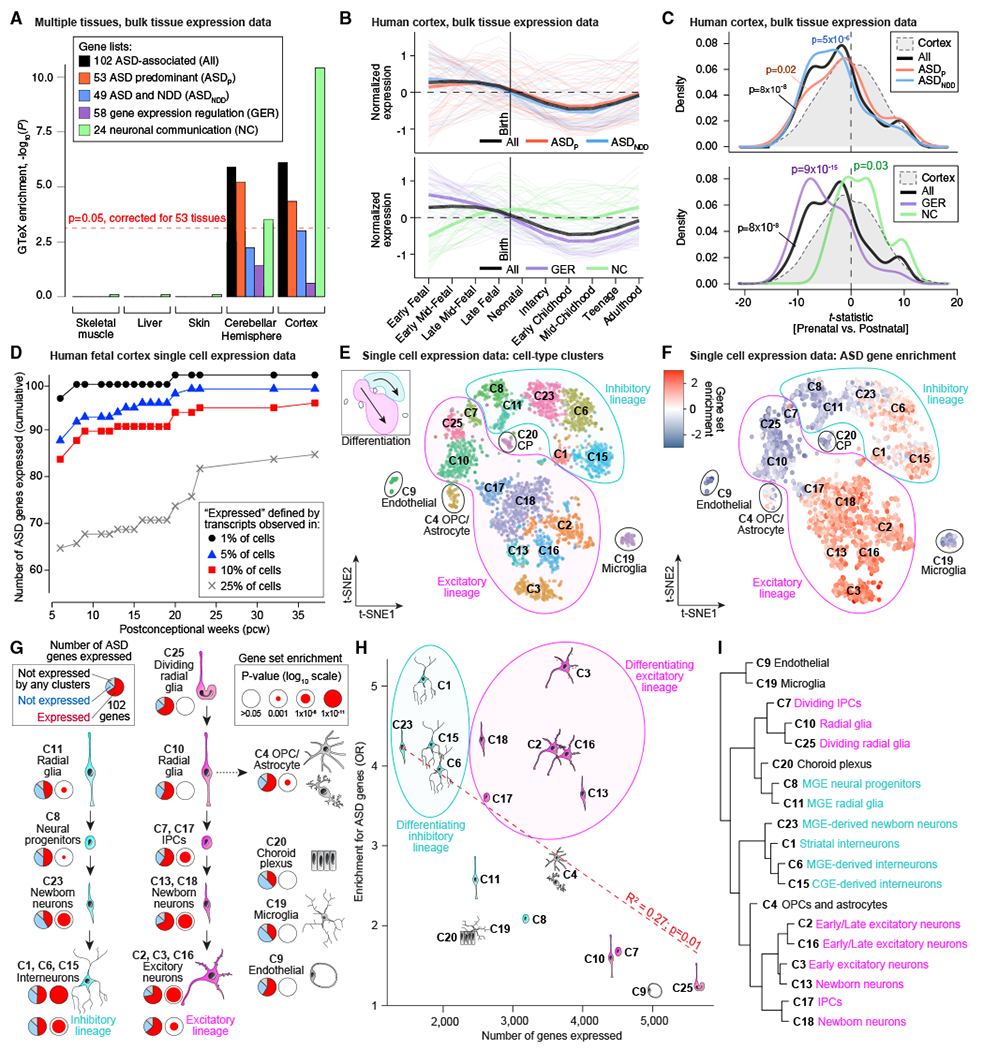
(A) GTEx bulk RNA-seq data from 53 tissues were processed to identify genes enriched in specific tissues. Gene set enrichment was performed for the 102 ASD genes and four subsets (ASD_P, ASD_NDD, GER, and NC) for each tissue. Five representative tissues are shown here, including cortex, which has the greatest degree of enrichment (OR = 3.7; p = 2.6 × 10⁻⁶).

(B) BrainSpan bulk RNA-seq data across 10 developmental stages was used to plot the normalized expression of the 101 cortically expressed ASD genes (excluding PAX5, which is not expressed in the cortex) across development, split by the four subsets.

(C) A t-statistic was calculated, comparing prenatal with postnatal expression in the BrainSpan data. The t-statistic distribution of 101 ASD-associated genes shows a prenatal bias (p = 8 × 10⁻⁸) for GER genes (p = 9 × 10⁻¹⁵), whereas NC genes are postnatally biased (p = 0.03).

(D) The cumulative number of ASD-associated genes expressed in RNA-seq data for 4,261 cells collected from human forebrain across prenatal development (Nowakowski et al., 2017).

(E) t-SNE analysis identifies 19 clusters with unambiguous cell type in these single-cell expression data.

(F) The enrichment of the 102 ASD-associated genes within cells of each type is represented by color. The most consistent enrichment is observed in maturing and mature excitatory (bottom center) and inhibitory (top right) neurons.

(G) The developmental relationships of the 19 clusters are indicated by black arrows, with the inhibitory lineage shown on the left (cyan), excitatory lineage in the middle (magenta), and non-neuronal cell types on the right (gray). The proportion of the 102 ASD-associated genes observed in at least 25% of cells within the cluster is shown by the pie chart, whereas the log-transformed Bonferroni-corrected p value of gene set enrichment is shown by the size of the red circle.

(H) The relationship between the number of cells in the cluster (x axis) and the p value for ASD gene enrichment (y axis) is shown for the 19 cell type clusters. Linear regression indicates that clusters with few expressed genes (e.g., C23 newborn inhibitory neurons) have higher p valuesthan clusters with many genes (e.g., C25 radial glia).

(I) The relationship between the 19 cell type clusters using hierarchical clustering based on the 10% of genes with the greatest variability among cell types.

Statistical tests: (A), t test; (C), Wilcoxon test; (E), (F), (H), and (I), FET.

Next, we developed a t-statistic that assesses the relative prenatal versus postnatal expression bias for each gene (STAR Methods). Cortically expressed ASD genes are enriched prenatally (p = 8 × 10⁻⁸, Wilcoxon test; Figures 5B and 5C). The ASD_P and ASD_NDD gene sets show similar patterns (Figure 5B), although ASD_NDD genes show more prenatal bias (p = 5 × 10⁻⁶, Wilcoxon test; Figure 5C). The GER genes display a marked prenatal bias (p = 9 × 10-¹⁵, Wilcoxon test; Figure 5C), reaching their highest levels during early to late fet al development (Figure 5B), whereas the NC genes show postnatal bias (p = 0.03, Wilcoxon test; Figure 5C), having their highest expression between late midfet al development and infancy (Figure 5B). Applying unsupervised co-expression network analysis (weighted gene co-expression network analysis; WGCNA) to the BrainSpan gene expression data yielded enrichment for cortically-expressed ASD genes within discretely co-expressed groups of genes (i.e., modules) across development (STAR Methods); however, GER and NC genes co-clustered separately (Figure S4; Table S5). Thus, in keeping with prior analyses (Chang et al., 2015; Parikshak et al., 2013; Willsey et al., 2013; Xu et al., 2014), ASD genes are expressed at high levels in the human cortex and early in development. The differing expression patterns of GER and NC genes could reflect two distinct periods of ASD susceptibility during development or a single susceptibility period when both functional gene sets are highly expressed in mid-to-late fet al development.

ASD Genes Are Enriched in Maturing Inhibitory and Excitatory Neurons

Prior analyses have implicated excitatory glutamatergic neurons in the cortex and medium spiny neurons in the striatum in ASD (Chang et al., 2015; Parikshak et al., 2013; Willsey et al., 2013; Xu et al., 2014). Here we perform a more direct assessment, examining expression of the 102 ASD-associated genes in an existing single-cell RNA-seq dataset of 4,261 cells from the prenatal human forebrain (Nowakowski et al., 2017), ranging from 6 to 37 post-conception weeks (pcw) with an average of 16.3 pcw (Table S5). We divided the cells into 17 developmental stages to assess the cumulative distribution of expressed genes by developmental endpoint (Figure 5D). For each endpoint, a gene was defined as expressed when at least one transcript mapped to this gene in 25% or more of cells for 1 or more pcw stage. By definition, more genes were expressed as fet al development progressed, 4,481 by 13 pcw and 7,171 by 37 pcw. Although the majority of ASD genes (68) were expressed by 13 pcw, the number increased to 81 by 23 pcw, consistent with the BrainSpan data (Figures 5B and 5C). More liberal thresholds for expression resulted in higher numbers of ASD genes expressed (Figure 5D), but the patterns were similar across thresholds and when considering gene function or cell type (Figure S4).

To investigate the cell types implicated in ASD, we considered 25 cell type clusters identified by t-distributed stochastic neighbor embedding (t-SNE) analysis, of which 19 clusters containing 3,839 cells were unambiguously associated with a cell type (Nowakowski et al., 2017; Figure 5E; Table S5) and were used for enrichment analysis. Within each cell type cluster, a gene was considered expressed when at least one of its transcripts was detected in 25% or more of cells; 7,867 protein-coding genes met this criterion. Contrasting one cell type with the others, ASD genes are enriched in maturing and mature neurons of excitatory and inhibitory line ages (Figures 5F and 5G). Early excitatory neurons (C3) expressed the most ASD genes (72; OR = 5.0, p < 1 × 10⁻¹⁰, Fisher’s exact test [FET]), whereas the choroid plexus (C20) and microglia (C19) expressed the fewest (39; p = 0.09 and 0.14, respectively; FET); 14 genes were not expressed in any cluster (Figure 5G). Within the major neuronal lineages, early excitatory neurons (C3) and striatal interneurons (C1) showed the greatest degree of enrichment (72 and 51 genes, respectively; p < 1 × 10⁻¹⁰, FET; Figures 5F and 5G; Table S5). Overall, maturing and mature neurons in the excitatory and inhibitory lineages showed a similar degree of enrichment, whereas the excitatory lineage expressed the most ASD genes, paralleling the larger numbers of genes expressed in excitatory lineage cells (Figure 5H). The only non-neuronal cell type with significant enrichment was oligodendrocyte progenitor cells (OPCs) and astrocytes (C4; 62 genes, OR = 2.8, p = 8 × 10⁻⁵, FET). Of the 62 genes expressed, 57 overlapped with radial glia, which share developmental origins with OPCs. These results are consistent with previous studies in post-mortem brain that identified dysregulation of gene expression in microglia but enriched expression of ASD risk genes only in neuronal cells (Ruzzo et al., 2019; Gandal et al., 2018a, 2018b; Voineagu et al., 2011). Furthermore, recent results for single-cell analysis in mid-gestation human brain development also highlight enrichment for ASD gene expression in both excitatory and inhibitory lineages (Polioudakis et al., 2019), along with some expression in non-neural cells without enrichment, as observed here. To validate the t-SNE clusters, we selected 10% of the expressed genes showing the greatest variability among the cell types and performed hierarchical clustering (Figure 5I). This recaptured the division of these clusters by lineage (excitatory versus inhibitory) and by development stage (radial glia and progenitors versus neurons).

Prediction of Novel Risk Genes and Functional Relationships among ASD Genes

ASD genes show convergent functional roles (Figure 4E) and expression patterns in the cortex (Figure 5B). Genes that are co-expressed with these ASD genes, interact with them, or are regulated by them could lend insight into convergent or auxiliary functions related to risk. In particular, we examined whether in silico network analyses would highlight additional risk genes and clarify the regulatory relationships between GER and NC genes. Three additional analyses were performed: the discovering association with networks (DAWN) approach to integrate TADA scores and gene co-expression data, enrichment analysis using protein-protein interaction (PPI) networks, and analyses using results from chromatin and cross-linked immunoprecipitation sequence assays to evaluate regulatory networks (STAR Methods; Figure S5; Table S5). Using the TADA results and BrainSpan gene co-expression data from the midfet al human cortex, DAWN yields 138 genes (FDR ≤ 0.005), including 83 genes that are not captured by TADA, with 69 of these 83 correlated with many other genes. Notably, 12 of the genes DAWN previously predicted as plausibly contributing to risk (De Rubeis et al., 2014) were identified as new TADA genes here (enrichment p = 8.4 × 10⁻¹¹; OR = 16.4). To explore whether GER and NC gene sets interact more than would be expected by chance, we analyzed PPI networks and found that they do not; there was an excess of interactions among all ASD genes (82 genes, p = 0.02, FET), GER genes (49 genes, p = 0.006), and NC genes (12 genes, p = 0.03) but not among GER and NC genes (2 genes, p = 1.00). GER genes did not regulate the NC genes, according to our analyses, although GER-GER regulation was enriched. Even CHD8, a prominent and well-characterized ASD GER gene, did not regulate NC genes more than expected by chance (Figure S5).

DISCUSSION

By characterizing rare de novo and inherited coding variation from 35,584 individuals, including 11,986 with ASD, we implicate 102 genes in risk for ASD at an FDR of 0.1 or less (Figure 2), of which 30 are novel risk genes. Notably, analyses of the 102 risk genes led to novel genetic, phenotypic, and functional findings. Evidence of several of the genes is driven by missense variants, including confirmed gain-of-function mutations in the potassium channel KCNQ3 and possible gain-of-function mutations in DEAF1, SCN1A, and SLC6A1 (Figure 3). Further, we strengthen evidence for driver genes in genomic disorder loci and propose a new driver gene, BCL11A, for the recurrent CNV at 2p15-p16.1. By evaluating GWAS results for ASD and related phenotypes and asking whether their common variant association signals overlap significantly with the 102 risk genes, we find substantial enrichment of GWAS signals for two traits genetically correlated with ASD—schizophrenia and educational attainment. For ASD itself, however, this enrichment is not significant, likely because of the limited power of the ASD GWAS. Despite this, KMT2E is significantly associated with ASD by both common and rare risk variation.

We performed a genetic partition between genes predominantly conferring liability for ASD (ASD_P) and genes imparting risk to both ASD and NDD (ASD_NDD). Three lines of evidence support the partition. First, cognitive impairment and motor delay are more severe in ASD subjects carrying mutations in ASD_NDD than in ASD_P genes (Figures 4B and 4C); second, inherited variation plays a lesser role in ASD_NDD than in ASD_P genes; and third, heterogeneity analysis demonstrates clear distinctions between the two groups of genes. Thus, ASD-associated genes are distributed across a spectrum of phenotypes and selective pressure. At one extreme, gene haploinsufficiency leads to global developmental delay with impaired cognitive, social, and gross motor skills, leading to strong negative selection (e.g., ANKRD11, ARID1B). At the other extreme, gene haploinsufficiency leads to ASD, and there is more modest involvement of other developmental phenotypes and selective pressure (e.g., GIGYF1, ANK2). This distinction has important ramifications for clinicians, geneticists, and neuroscientists because it suggests that clearly delineating the effect of these genes across neurodevelopmental dimensions could offer a route to deconvolve the social dysfunction and repetitive behaviors that define ASD from more general neurodevelopmental impairment. Larger cohorts will be required to reliably identify specific genes as being enriched in ASD compared with NDD.

Single-cell gene expression data from the developing human cortex implicate mid-to-late fet al development and maturing and mature neurons in both excitatory and inhibitory lineages in ASD risk (Figure 5). Expression of GER genes shows a prenatal bias whereas expression of NC genes does not. Placing these results in the context of multiple non-exclusive hypotheses around the origins of ASD, it is intriguing to speculate that the NC ASD genes provide compelling support for excitatory-inhibitory imbalance in ASD (Rubenstein and Merzenich, 2003) through direct effects on neurotransmission. However, because there was no support for a regulatory role for GER ASD genes on either NC or cytoskelet al ASD genes, additional mechanisms having to do with cell migration and neurodevelopment also appear to be at play. This might suggest that GER ASD genes affect the excitatory-inhibitory balance by altering the numbers of excitatory and inhibitory neurons in given regions of the brain. ASD must arise by phenotypic convergence among these diverse neurobiological trajectories, and further dissecting the nature of this convergence, especially in the genes we identified here, is likely to hold the key to understanding the developmental neurobiology that underlies the ASD phenotype.

STAR★METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Joseph D. Buxbaum (joseph.buxbaum@mssm.edu).

MATERIALS AVAILABILITY

This study did not generate new unique reagents.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Overview of the Autism Sequencing Consortium cohort

The Autism Sequencing Consortium (ASC) is a large-scale international genomic consortium integrating ASD cohorts and sequencing data from over one hundred investigators (Buxbaum et al., 2012; https://genome.emory.edu/ASC/).

At the outset, the ASC aggregated data from ASC sites, but over the past several years it has also been able to sequence samples at the Broad Institute/Massachusetts General Hospital through the Broad Center for Common Disease Genomics (UM1HG008895, Mark Daly, PI).

The analysis presented here is based on 35,584 unique human samples collected from 32 distinct sample sets (Table S1). These include cohorts sequenced by the Autism Sequencing Consortium (ASC) and published in our first (De Rubeis et al., 2014) or second study (Lim et al., 2017) (Germany, Japan, PAGES, Pittsburgh, Seaver, Spain, TASC, and UCSF), as well as new collections (Boston, Brazil, CHARGE, Chicago, Hong Kong, Miami, Portugal, Rome, Siena, Turin, UC Irvine, and Utah), with a total of 6,197 newly collected and sequenced samples included in our final analysis. We also sequenced samples from the Autism Genetic Resource Exchange (AGRE), the Boston Autism Consortium, two sites in Finland, and Swedish controls from epidemiological studies in schizophrenia and bipolar disorder. We imported exome sequence data from the Simons Simplex Collection (Iossifov et al., 2014), as well as an unpublished Norwegian cohort, and included them in our dataset alongside ASC-sequenced samples.

In addition, we incorporated published de novo variants from the UK10K consortium, the University of Pennsylvania, Vanderbilt University, and a collection of samples from the Middle East. Finally, we integrated gene-level variant counts from autism cases and matched controls from the iPSYCH research initiative (Lauritsen et al., 2010; Pedersen et al., 2018; Satterstrom et al., 2018). A description of each cohort, with the number of samples sequenced and the number used in our analyses, its ascertainment and diagnostic strategy, and associated references is found in Table S1. This table also contains details on the family relationships, sex, and phenotypic status of all samples.

Informed consent and study approval

The ASC and ASC sites are approved by appropriate Institutional Review Boards or Ethical Committees and informed consent was obtained from all subjects. The individual studies that contribute to the ASC may have directly ascertained and interviewed human clinical subjects, along with controls, in accord with the ethical principles and practices of modern biomedical research. In contrast to contributing sites, the ASC as a group has a different relationship to human subjects. The ASC has no direct contact with the research subjects and no identifying information is provided by the primary sites to the ASC. From the perspective of the ASC, all data is de-identified and effectively anonymized.

For samples provided to the ASC sequencing site (Broad-MGH through their funding from NHGRI), a copy of the consent(s) and a signed IRB Data Use Letter (DUL) was received before samples were accepted. The DUL confirms that the samples can be shared and are suitable for upload to dbGaP and NDAR.

The iPSYCH study was approved by the Regional Scientific Ethics Committee in Denmark and the Danish Data Protection Agency.

METHOD DETAILS

Exome sequencing and data processing

The bulk of new ASC samples were sequenced at the Broad Institute on Illumina HiSeq sequencers using the Illumina Nextera exome capture kit. The remainder were sequenced at three other sites: the University of California, San Franciso (N = 495), the Sanger Institute (N = 443), and Johns Hopkins University (N = 302), all using similar methods. Sequencing reads were aligned to human genome build 37 (GRCh37/hg19) using the Burrows-Wheeler Aligner (BWA, Li and Durbin, 2009), aggregated into a BAM file. Picard (http://broadinstitute.github.io/picard/) was used for sorting by chromosome coordinates and marking duplicates. Single nucleotide variants (SNVs) and insertions / deletions (indels) were jointly called across all samples using the Genome Analysis Toolkit (GATK; Van der Auwera et al., 2013) HaplotypeCaller package version 3.4. Variant call accuracy was estimated using the GATK Variant Quality Score Recalibration (VQSR) approach. The VCF file (format v4.1) was produced by the Broad sequencing and calling pipeline with GATK version 3.4 (g3c929b0).

QUANTIFICATION AND STATISTICAL ANALYSIS

Dataset Quality Control

The VCF file, containing approximately 29,000 exomes, was loaded into Hail 0.1 (https://hail.is/; https://github.com/hail-is/hail) to perform basic quality control steps. Multi-allelic sites were split into bi-allelic sites and each variant was then annotated with the Variant Effect Predictor (VEP, McLaren et al., 2016) by prioritizing coding canonical transcripts. VEP assigned properties such as gene name and consequence to each variant. An overview of the quality control and data cleaning process is shown in Figure S1.

Round 1, sample-level quality control

To check the accuracy of the reported pedigree information, relatedness was calculated between each pair of samples using Hail’s ibd() function and sex was imputed for each sample using Hail’s impute_sex() function. The relatedness values were input into the program PRIMUS (Staples et al., 2014), which inferred pedigree structure. Combined with the imputed sex, these inferred pedigrees were compared to reported pedigrees and checked for discrepancies. Obvious errors in reporting were fixed (e.g., swapped mother/ father or parent/child labels in the same family), and samples with a discrepancy that could not be resolved (~200) were dropped. Parents without a child in the dataset (~250) were also dropped, resulting in 28,547 samples and 5,420,608 unique variants.

Round 1, variant-level quality control

Low-complexity regions were removed (110,963 variants), as were SNVs that failed VQSR (265,130 variants), leaving 5,044,515 unique variants. For genotype quality control, several filters were applied: we filtered calls with a depth less than 10 or greater than 1,000; for homozygous reference calls, we filtered genotypes with less than 90% of the read depth supporting the reference allele or with a genotype quality less than 25; for homozygous variant calls, we filtered genotypes with less than 90% of the read depth supporting the alternate allele or with a Phred-scaled likelihood (PL) of being homozygous reference less than 25; and for heterozygous calls, we filtered genotypes with less than 90% of the read depth supporting either the reference or alternate allele, with a PL of being homozygous reference less than 25, with less than 25% of the read depth supporting the alternate allele (i.e., an allele balance less than 0.25), or with a probability of the allele balance (calculated from a binomial distribution centered on 0.5) less than 1×10⁻⁹.We additionally filtered any heterozygous call in the X or Y non-pseudoautosomal regions in a sample that imputed as male. For samples imputed as female, calls from the Y chromosome were removed. After applying these filters and removing sites that were no longer variant, the dataset contained 28,547 samples and 4,755,048 unique variants.

Round 2, sample-level quality control

We applied further sample-level quality control filters using the filtered variants. We removed samples with estimated contamination levels using FREEMIX > 7.5% (20 samples) (Jun et al., 2012) or chimeric reads > 7.5% (121 samples). Stratifying samples into 18 different batches (by exome capture/year/cohort/sequencing center, see Table S1), samples were filtered if their call rate was greater than 3 standard deviations below the group mean (300 samples). Duplicate samples were then removed (761 samples), as were samples for which the imputed sex did not match the reported sex (59 samples). Following these sample filters, family structures were reevaluated: if one or more parents of a case in the family-based data (which we also refer to as a “proband”) had been filtered, the proband was reclassified as a case in the case-control data and the remaining parent (if any) was dropped; if the proband had an unaffected sibling, the sibling was kept as a “sibling of case” (not used in this study); if one or more parents were filtered and no proband remained, then data for remaining family members were removed; and relatives not relevant for calling de novo variants (such as aunts or uncles) were removed. After applying these rules, the dataset contained 5,833 complete families, with 5,924 affected probands, 2,007 unaffected offspring, 5,834 fathers, and 5,833 mothers (one family contained two probands, two fathers, and one mother).

The dataset also contained 2,388 cases, 106 siblings of cases, and 4,324 controls, none of whom were part of a complete trio. To prevent complicated patterns of dependency, we excluded all but one sample (or one case-sibling pair) from each group of related samples within these categories. We defined related samples using a KING (Manichaikul et al., 2010) kinship value of 0.1 or greater, approximately equivalent to a Pi-Hat of 0.2 or greater. After this filtering, the dataset contained 2,353 cases, 100 siblings of cases, and 4,316 controls, for a total of 26,367 samples.

Round 2, variant-level quality control

After filtering sites that were no longer variant due to sample exclusion, there were 4,605,130 unique variants. For a second round of variant quality control, variants with call rate < 10% (17,083 variants) or a Hardy-Weinberg equilibrium p value less than 1×10⁻¹² (27,862 variants) were excluded, leaving 26,367 samples and 4,560,185 unique variants. This dataset was then used as the starting point for the de novo, inherited, and case-control workflows.

Defining rare and de novo variants

De novo variation

De novo variants were called from the 26,367-sample dataset described above, including 5,924 affected probands and 2,007 unaffected offspring (7,931 total children). After filtering any genotype with a GQ < 25, de novo variants were called using the de_novo() function of Hail 0.1, which implements the caller used in previous ASC work (https://github.com/ksamocha/de_novo_scripts). Population allele frequencies for variants were obtained from the non-psychiatric subset of gnomAD (https://gnomad.broadinstitute.org/) and these frequencies were used as the input priors. As additional parameters, parents’ homozygous reference genotypes were required to have no more than 3% of reads supporting the alternate allele, children’s heterozygous calls were required to have at least 30% of reads supporting the alternate allele, and the ratio of child read depth to parental read depth was required to be at least 0.3.

This process identified 44,562 putative de novo variants at 26,577 distinct genomic locations in the 7,931 children in the dataset. Of the 7,931 children, 519 were also part of a whole-genome sequencing project (Werling et al., 2018), and we added a further 168 de novo variants called in protein-coding regions of these samples from the whole-genome sequencing that were not called in the exome sequencing. We also incorporated 338 previously published and validated de novo variants in our samples that were not identified by our caller (Kosmicki et al., 2017). Thus, in total, we had 45,068 putative de novo variants at 27,083 distinct loci in 7,931 children. For quality control on the de novo variants, we retained variants if they were high confidence as indicated by the calling algorithm, medium confidence and a singleton in the dataset, or previously experimentally validated (20,862 putative de novo variants included). To remove calls stemming from cell line artifacts, an allele balance of at least 0.4 was required for the 773 probands and 40 siblings for whom data were generated from immortalized cell line DNA (2,171 putative de novo calls excluded). Next, a call was removed if it had an allele frequency > 0.1% across the samples in our dataset, in the non-psychiatric subset of ExAC (r0.3, http://exac.broadinstitute.org/), or in the non-psychiatric subset of gnomAD (5,068 putative de novo variants excluded). Calls were excluded if they appeared more than twice in the remaining list of putative de novo variants (403 putative de novo variants excluded) and were then limited to one variant per person per gene (570 putative de novo variants excluded), retaining variants with the most severe consequence when selecting which one to keep. Finally, samples whose DNA source was whole-blood or saliva were excluded if they had more than seven protein-coding putative de novo variants (20 out of 5,143 probands and 13 out of 1,967 unaffected children excluded). Samples whose DNA source was immortalized cell lines were dropped if they had more than five protein-coding putative de novo variants (35 out of 773 probands and 1 out of 40 unaffected children excluded). After applying these filters, the remaining list of high confidence de novo variants included 14,569 de novo variants from 5,869 probands and 1,993 unaffected children. To maximize power and improve consistency with prior analyses, we supplemented this set with 933 and 287 published de novo variants in 561 probands and 186 siblings (De Rubeis et al., 2014; Sanders et al., 2015; Kosmicki et al., 2017), respectively, for whom original sequence data were not available. The final list of high confidence de novo variants included 15,789 de novo variants from 6,430 probands and 2,179 unaffected children (Table S1; Figure S1).

Rare inherited variation

As with de novo variation, we used the dataset of 26,367 samples and 4,560,185 unique variants described above as a starting point to identify high confidence rare inherited variants. Any genotype call with a GQ < 25 was removed and heterozygous genotypes were required to have an allele balance ≥ 0.3. Variants were required to have a call rate ≥ 90%, insertions and deletions were required to pass VQSR, and SNVs were required to have a VQSLOD (variant quality score log odds) ≥ −2.085. The VQSLOD threshold for SNVs was determined by identifying the threshold at which synonymous variants with an allele count of 1 among parents in the dataset were transmitted to the child 50% of the time, as described previously (Lek et al., 2016; Kosmicki et al., 2017). Protein-truncating variants were required to be high confidence (“HC”) by the LOFTEE plugin for VEP and to have no LOFTEE flags other than “SINGLE_EXON.”

For the purposes of gene-level counts, variants were tallied in the 5,869 probands and 1,993 unaffected children with exome sequencing data available who passed quality control for de novo variation above. Variants were required to have an allele count ≤ 5 in the combined parents, cases, and controls (18,153 people) in our dataset, as well as an allele count ≤ 5 in the non-psychiatric subset of ExAC (see Figure S1).

Rare case-control variation

For samples that were not in complete trios, rare variants were filtered using the same metrics and thresholds as rare inherited variants (above). For purposes of gene-level counts, rare variants were defined using the same allele frequency thresholds as rare inherited variants: allele count ≤ 5 in the 18,153 combined parents, cases, and controls in the dataset, as well as an allele count ≤ 5 in the non-psychiatric subset of ExAC (see Figure S1).

To ensure well-matched cases and controls, probable ancestry was calculated by merging our raw dataset with genotypes from the 1000 Genomes Project and conducting principal components analysis (PCA) in Hail on a set of ~5,000 common SNPs. A naive Bayes classifier was trained (using the naiveBayes function from the R package e1071) on the 1000 Genomes samples and used to predict which of our samples clustered with the populations labeled as European or East Asian. Rates of synonymous variants were well-matched between cases and controls from the Swedish contributing site, which were classified European (745 cases and 3,595 controls), as well as between cases and controls from the Japanese contributing site which were classified East Asian (196 cases and 298 controls). For inclusion in TADA, we counted variants from the 4,340 Swedish samples. Overall variant rates were higher in the Japanese samples than the Swedish samples, possibly because our filtering was based on allele counts in ExAC, and ExAC has less representation from East Asian samples than European ones.

Analysis of variant classes

To model a qualitative trait—in this case, the presence or absence of ASD—using standard quantitative genetics concepts, we imagine that there is an unobserved, normally distributed variable called “liability” that determines whether or not an individual is diagnosed with ASD (Falconer, 1965). We assume that liability, L, has mean 0 and variance 1 in the general population. Individuals with L greater than some threshold t are diagnosed with ASD and individuals with L<t are considered “typical.” Under this model, the prevalence difference between males and females is viewed as a difference in thresholds for males and females. For a male to be diagnosed with ASD, his liability must be larger than t_m. For a female to be diagnosed with ASD her liability must be larger than t_f. Since ASD is more common in males than females, we conclude that t_m<t_f. For all that follows we will assume that the prevalence of ASD in males, Ψ_m, is 1 in 42 (implying t_m ~ 1.98), and the prevalence of ASD in females, Ψ_f, is 1 in 189 (implying t_f ~ 2.56) (Baio et al., 2018). We model ASD+ID similarly, but with lower prevalence than all ASD (male prevalence 0.00499; female prevalence 0.00138).

When considering the effects of individual alleles on liability, we employ an elaboration to the standard quantitative genetics model, which is sometimes called the “mixed model of inheritance” (Morton & MacLean, 1974). We assume that individual alleles make additive contributions to liability, so that for some allele, A₁, individuals with 0 copies of the allele have mean – μ, variance 1 liability, but individuals with 1 copy have mean α – μ, variance 1, and individuals with 2 copies have mean 2α – μ, variance 1 liability. Assuming Hardy-Weinberg equilibrium for genotypes, and the frequency of A₁ equaling p, μ = 2αp² + α2pq = 2αp. Here μ is a normalizing factor to ensure the overall population has mean liability 0.

For several of our analyses we are interested in the effect, α, for variants of a particular type in a collection of genes, for instance de novo PTVs in genes with pLI scores ≥ 0.995. If a variant is individually exceptionally rare, we have virtually no power to estimate its individual effect size, but over a large collection of such variants average properties are estimable. To do so, we model the entire collection of variants as if there were a single allele with frequency equal to the sum of the individual variant frequencies. This approach makes little sense for common variants, but for sufficiently rare variants, where single individuals seldom harbor more than one, this is a reasonable and helpful approximation. For some variant types, however, such as silent variants, the count of alleles can be substantial. For this reason, rather than standardize by 2N, where N is the number of subjects, we standardize by 2NM, where M = 17,484 is the number of autosomal protein-coding genes analyzed herein. This standardization has no material impact on calculations of parameters of interest. To distinguish between cases and controls, we write N_ca and N_co respectively.

Thus, for each type of variant we are interested in studying, e.g., de novo PTV mutations, we count the number of observations of this class of variant in cases (our probands in trios), and the number of observations of this class of variant in controls (our siblings in trios). For a given type of variant, V, we call Pr{V |D} the frequency of this type of variant in cases (observed number of variants divided by 2NM), and Pr{V | ¬D} the corresponding value in controls. We make these calculations separately in males and females, which we denote as Pr{V_m |D_m}, Pr{V_f |D_f}, Pr{V_m | ¬D_m}, and Pr{V_f | ¬D_f}, where the m and f subscripts distinguish male and females. The overall frequency of the variant class can be found by:

$$\mathrm{Pr}\{V_g\}=\mathrm{Pr}\{V_g|D_g\}{\psi }_g+\mathrm{Pr}\{V_g|\neg D_g\}(1-{\psi }_g)$$

where g can be either f or m, for females and males, respectively. From this the Penetrance (probability of disorder given variant) of the variant class can be found immediately by Bayes rule:

$$\mathrm{Pr}\{D_g|V_g\}=\frac{\mathrm{Pr}\{V_g|D_g\}{\psi }_g}{\mathrm{Pr}\{V_g\}}$$

To find the average effect, α_Vg, of this variant class we note:

$$\mathrm{Pr}\{D_g|V_g\}=\underset{t_g-{\alpha }_{vg}}{\overset{\infty }{\int }}\frac{1}{\sqrt{2\pi }}e-\frac{x^2}{2}dx$$

This is the area under the curve of a normal distribution with mean α_Vg and variance 1, from the threshold t_g to infinity. In other words, the penetrance of a genotype is the fraction of the genotype’s liability distribution that exceeds the disorder threshold. We can find the effect size (average liability of the genotype) by inverting a standard normal cumulative distribution, Φ(x):

$$a_{Vg}=t_g-{\Phi }^{-1}(1-\mathrm{Pr}\{D_g|V_g\}).$$

In this manner, we go from observable quantities (prevalence, genotype frequency, and frequency of genotype among cases only) to a variant type’s unobserved but inferred effect on the liability scale. Empirically, the relative risk for the variant type is calculated as Pr{V|D}/Pr{V | ¬D} for the contrast of cases versus controls. To assess whether or not there is any difference in this variant class between cases and controls, we perform an exact binomial test on the underlying observed counts, where the probability of success is given by N_ca/(N_ca + N_co). The odds ratio is computed from four observations, the number of variants of the risk class in cases, a; the number of variants of the risk class in controls, b; the number of alleles not in the risk class in cases 2N_caM – a; and the parallel calculation for controls, 2N_coM – b.

To estimate a confidence interval of α_Vg, we note that in a very formal sense a_Vg is the average effect on the liability scale of the variant. Were we able to observe those effects directly, we could have calculated the observed mean and standard error of those effects. Because we cannot observe liability directly here, we infer the standard error of α_Vg by the following procedure: map the p value from the binomial test, described above, onto an equivalent z-value from the normal distribution, z; then α_Vg/z is a reasonable estimator for the standard error of the estimator for α_Vg.

For Table S1, calculations for “All Genes” and for “Other Genes” were performed separately for males and females and also separately for the PAGES and DBS (iPSYCH) samples. Inherited analysis calculations were also separated by male and female and by proband and sibling. To combine effects between males and females, we took inverse-variance weighted averages of male and female effect sizes. We performed analogous calculations for the populations of case-control samples. For these calculations for the 102 ASD genes, however, because the counts of events were often small, we combined data over males and females and over PAGES and DBS samples to compute overall parameters (i.e., performed mega-versus meta-analysis). When parameters could not be estimated, this is noted as NA. Selected results are shown in Figure 1 and Figure 2.

Transmission and De Novo Association Test (TADA)

Background

Published analyses of whole exome sequencing (WES) data using TADA have evaluated two categories of rare variation, namely protein-truncating variants (PTVs; i.e., frameshift, stop gained, canonical splice site disruption) and “probably damaging” missense variants according to PolyPhen-2 (Mis3) (Adzhubei et al., 2010), in the context of three categories of inheritance pattern: de novo, inherited, and case-control. TADA requires a mutational model (Sanders et al., 2012; Neale et al., 2012; Samocha et al., 2014) which accounts for gene size and sequence composition to obtain an expectation for mutations per gene, given sample size. It treats all PTVs within a gene as equivalent, although their impact on risk is allowed to vary across genes and inheritance patterns (likewise for Mis3). TADA first computes a gene-specific Bayes factor for each mutation category and inheritance pattern, and then it multiplies these Bayes factors to generate a statistic that summarizes all evidence of association for each gene. The total Bayes factor is finally converted to a q-value to control false discovery rate (De Rubeis et al., 2014). As a Bayesian model, TADA requires prior parameters or hyperparameters, namely the fraction of genes in the genome affecting risk, thus far taken to be 0.05, and γ, the relative risk for a particular mutation category. See He et al. (2013) for estimators.

Evaluating TADA and False Discovery Rate (FDR)

For downstream analysis it is critical to ensure reliable performance of TADA so that risk gene lists, such as those with FDR < 10%, are properly calibrated. Such guarantees are straightforward to prove in many settings (Efron, 2012). In the WES setting, however, and especially for the relatively discrete counts of de novo events, a demonstration that the FDR rate holds is warranted. It is worth noting that, even though there are many genes that contain no mutations, the mutation rate is gene-specific and varies with gene length. Consequently, with the exception of the genes with a signal, the p values from the TADA analysis of PTV and Mis3 mutations are almost uniformly distributed (Figure S2A).

To evaluate the validity of the FDR framework in the context of TADA analysis, we conduct “empirical-known signal experiments” (EKSE). The idea is to perform TADA analyses in which the true signal is known a priori. To make the simulation as real as possible, it is performed using real de novo mutation counts as a base. These mutations are chosen to carry no detectable signal (i.e., mimicking the null distribution because they are believed to be non-functional). Simulated signals for association are then generated for randomly selected genes. Once the data are generated, TADA is used to analyze them and the resulting FDR and other features of the method are examined.

EKSE Simulations to Assess the Properties of FDR

For these empirically-known signal experiments, we let synonymous variants play the role of Mis3 (denoted as Mis3new) and “benign” missense variants according to PolyPhen-2 (Mis1) play the role of PTV (denoted as PTVnew). Signals are layered onto genes that are randomly chosen. Below is the detailed procedure:

1. Divide all 17,484 autosomal protein-coding genes into 20 bins of equal size. Let b = 1 20.

2. For each of the 20 bins, iteratively generate a signal for all genes in the bin; the remaining 19 bins, with no signal, represent the null genes. The extra signal in the ith gene for both new kinds of de novo variants is simulated using X_i | γ_i ~ Poisson(2μ_i(γ_i – 1)N), where γ_i ~ Gamma(γ, β). The hyperparameters are selected to yield signals similar to the real data: β = 0.2 and γ is set to be 2.4 and 5.4 for Mis3new and PTVnew respectively, and N = 6,430. The “−1” in the Poisson equation is to account for the observed de novo variants already included from the real data. The simulated de novo events are added to the observed Mis3new and PTVnew to create each of the 20 datasets.

3. Perform TADA analysis for each of the 20 datasets.

4. Display the resulting q-FDR curves for b = 1 20, and q-FDR averaged over b.

Pure Simulations to Assess the Properties of FDR

This simulation is closely related to EKSE. The only difference is that the null mutations are generated randomly from a multinomial distribution instead of adopted directly from the synonymous and Mis1 variants. The procedure is described below:

1. Randomly sample a fraction of all 17,484 autosomal protein-coding genes as signal genes, denoted as set S. We set the fraction as π = 0.05. The number of trios is N = 6,430.

2. For both new types of variants, Mis3new and PTVnew, the mutations of all the genes are randomly generated from a multinomial distribution, X ~ Multinom(M, p), where the probability vector p is proportional to p = {μ_iγ_i}_{i=1,…,17484}, where γ_i ~ Gamma(γ, β) if i∈S, otherwise equals 1. The total number of mutations is $M=2N{\displaystyle \sum _{i=1}^{17484}}{\mu }_i{\gamma }_i.$ The mutation rates of Mis3new are taken from synonymous variants, and the mutation rates of PTVnew are taken from Mis1. The hyperparameters γ, β are set to be the same as in EKSE.

3. Perform TADA analysis on the two generated types of variants. Display the resulting q-FDR curve.

4. Repeat steps 1-3 one hundred times.

Results of simulations

Figure S2B shows the averaged actual FDR versus the q-value over the 20 EKSE experiments. The error bars are obtained from the pure simulation. For q < 0.1 the average curve follows the diagonal line (roughly), which indicates that the actual FDR is well controlled in the region of primary interest. We do detect a slight bump in the actual FDR forq > 0.1. To understand this deviation, we compared the observed counts for synonymous (Mis3new) and Mis1 (PTVnew) to simulated counts generated from the model.

The distribution of the number of genes with synonymous counts ≥3 and Mis1 counts ≥2 is contrasted with the observed counts (Figure S2C). The contrasts show that there is a slight excess of multiple hits in the observed counts compared to the model. Adding counts of synonymous and Mis1 mutations we obtain a single distribution of mutations per gene and find that there is an excess of counts of 0, 2, 3, and >3 and a relative lack of counts of 1; overall the counts are fairly similar, but they differ significantly from expectations (chi-square p value = 0.012). The 8 null genes with the strongest TADA signal are GNS, LRRFIP1, GALC, GRN, MYH9, FOXK2, AP1B1, and UNC45B, and these are the genes that contribute to the bump in the FDR. However, none of these genes are significant (q< 0.1) in the EKSE analysis or in the actual data analysis of Mis3 and PTV mutations. From this EKSE experiment we conclude that the TADA model does not perfectly capture reality and the actual FDR deviates slightly from reported value for values of q > 0.1. This deviation is likely due to inexact estimates of the per gene mutation rate.

TADA relies on a mutation rate model for genes, which is an estimated quantity. Hence, we evaluate the impact of misspecification of mutation rates. To quantify the deviation from the expected null distribution due to mutation rate misspecification, we use the theory of genomic control (Devlin and Roeder, 1999), specifically estimating the inflation factor λ_GC. In this experiment, we randomly select 10%–50% of genes and artificially make the nominal mutation rates increasingly lower than their actual estimated rates. This will make the observed mutation count larger than the expected count for a subset of genes. The result is that test statistics for association will tend to be increased for some genes, and the larger the discrepancy, the larger the set of test statistics that do not follow the expected null distribution. The genomic control factor, based on the z-statistics from the TADA analysis (Figure S2D), quantifies this inflation. As expected, the genomic control factor increases as more genes are analyzed with lowered nominal mutation rates (Figure S2E). The inflation for λ_GC is modest, however, even for these fairly notable misspecifications of the mutation rates.

Because TADA is a Bayesian method, it is more natural to use FDR than a Family-Wise Error Rate (FWER) cutoff to determine significance. In this gene discovery setting it is informative to compare the numbers of true discoveries (TD), false discoveries (FD), and FDR for different p value and FDR thresholds and to examine the impact of model mis-specifications on FDR (Figure S2F). We measure discrepancies via the genomic control factor (λ_GC). We simulate the Z-value of 20,000 genes, 5% with a signal from N(μ, λ_GC) and 95% from the null N(0,λ_GC), where λ_GC varies from 1 to 1.2. The value of μ is chosen to be 2 to approximately mimic the real data. Based on 1,000 replications, we calculate the average TD, FD, and FDR for a Bonferroni-adjusted p value threshold and different FDR thresholds. As expected, FWER has considerably fewer FD but also notably fewer TD than FDR, and the observed FDR is well calibrated when λ_GC = 1 (Figure S2F). (For λ_GC = 1, TD = 5, 52,113, 334, and FD = 0.1,3,13, and 144 for the four thresholds examined. In each case the error rate is controlled at the expected rate.) However, as λ_GC increases the actual FDR increases rapidly, especially for larger q-values. In contrast, FWER is fairly well controlled even for model discrepancies.

Next, again by using simulations, we investigate how varying the number of risk genes impacts q-values for genes near but not over the FDR threshold. The key idea is to examine how the q-values of the borderline genes—defined to be genes with 0.05 < q < 0.1 — vary as π, the fraction of signal genes, changes. We expect that, as π increases, q-values of genes near the threshold will decrease. Indeed, we observe that the q-values of both non-signal (Figure S2G) and signal (Figure S2H) borderline genes decrease as π increases, but the impact on the non-signal borderline genes is not substantial and q-values for only a few of these genes cross the threshold.

A more powerful TADA model (TADA⁺)

TADA requires input of several parameters, most notably the relative risk, γ. To estimate the relative risk for a category of mutations, we use the burden-relative risk relationship derived in He et al. (2013): γ = 1 + (λ – 1)/π, where π = 0.05 is the estimated fraction of risk genes and the burden π is calculated by comparing mutation counts in probands and unaffected siblings. Because differences in sequencing depths and variant calling procedures may lead to systematic differences in mutation rates, we normalize the counts using synonymous mutations counts. Let x and S be the number of mutations in the category of interest and compare the counts in cases (cs) and controls (cn) as λ = (x_csS_cn)/(x_cnS_cs).

Previous TADA analyses (De Rubeis et al., 2014; Sanders et al., 2015) used two annotation categories, PTV and Mis3. Here we develop a more powerful version of TADA, which uses additional annotation information. For clarity we will label the original version TADA^O and the refined model TADA⁺.

Recent studies have refined our understanding of what variation is likely to be meaningful for risk in two ways. Regarding PTVs, Kosmicki et al. (2017) showed that signals carried by PTVs involve a subset of genes that are evolutionarily constrained. For these genes, the population tends to have far fewer PTVs than would be expected based on gene size, base-pair content, and evolutionary models. This constraint feature of genes is embodied in pLI (the probability of being loss-of-function [aka PTV] intolerant) (Lek et al., 2016), which is a metric ranging from zero to one, with a larger pLI representing a greater dearth of PTV variation. Kosmicki et al. (2017) found that genes with pLI > 0.9 tend to harbor most of the ASD association signal from PTVs. In this work, we model the relative risk (γ) of de novo PTVs as a continuous function of pLI. Figure S2I shows γ as a function of pLI, where the x axis has been converted using the inverse normal transformation, but the original values of pLI are given. We create seven bins of data and fit a logistic curve to the data. The dots are the data and the black line is the fitted curve. Then we compute error bars based on the 95% prediction interval around the fitted curve. In the upcoming implementation we truncate γ at the null value of one.

More refined information is also available for missense variants. Samocha et al. (2017) recently introduced the MPC score, a missense deleteriousness metric composed of “Missense badness,” PolyPhen-2 (Adzhubei et al., 2010), and Constraint. This metric also uses the concept of evolutionary constraint and seeks to quantify the degree of constraint for all missense variation in the genome. To determine how MPC might be used in TADA, we compute the average relative risk (g, the hyperparameters for TADA) for a moving window of MPC in the ASC data (Figure S2J). Using a window over probands’ missense variants ordered by MPC score, and with a width of 7.5% of the variants, we obtain the curve showing the average relative risk as a function of MPC score. Three levels of g naturally emerge from this relationship, with the first level (MPC < 1) being close to marginal relative risk and two levels showing evidence for excess burden in ASD (Figure S2J). Based on the nature of these results, we chose to group missense mutations into two categories for TADA, using established thresholds of MPC (Samocha et al., 2017): 1 ≤ MPC < 2 (MisA) and MPC ≥ 2 (MisB). Note that missense variation with MPC < 1 is treated as benign. The relative risk for each of the two missense categories is computed directly from the data (He et al., 2013) as γ_MisA = 4.18 and γ_MisB = 22.15. We note that other tools for variant classification have been recently published (Havrilla et al., 2019), and MPC score has been shown to have a comparable performance to these methods.

Besides the de novo variants, we also consider PTVs from case-control data by aggregating the iPSYCH (Danish) data and PAGES (Swedish) data. Following the same procedure as for de novo PTVs, within seven bins, we estimate the relative risks for the two case-control datasets separately and combine them with a precision weight. We then fit a logistic curve using the seven points to smooth γ as a continuous function of pLI (Figure S2K). In the TADA analysis, we treat g of each gene as fixed for case-control data to achieve closed-form solutions and thus facilitate computation.

These analyses define three categories of variation that are potentially meaningful for risk. The gene-specific mutation rates for PTVs and missense variants have been reported previously (Lek et al., 2016), and we further estimated the mutation rates for MisA and MisB. With mutation rates and hyperparameters estimated above, the refined TADA model can be applied to the data to identify risk genes for ASD. To allow for more variability in the prior for γ, we set β = 0.2.

To resolve an emerging issue with the model’s Bayes factor (BF) values, we implement a floor adjustment that imposes a lower bound of 1 on all BF. The issue is that for some genes with larger mutation rates and zero de novo MisB mutations, the MisB BF is substantially lower than 1. Multiplying this with the other evidence renders those genes not significant. Indeed, with the mutation rates provided and the high relative risk of MisB, the model clearly expected to observe at least one de novo MisB variant. (This happens for other categories as well, but most notably for MisB.) We think the problem is heterogeneity of genes—some genes with a de novo PTV just do not have MisB mutations in the data, even though these mutations are expected. It does not make sense to have the observation of no mutations drive the model. To circumvent the problem, we made a modification of the method so that BF is replaced by max(1,BF). We tested this in simulations and the size of the modified test is satisfactory (see the discussion in the next section).

TADA⁺ incorporates all of the refinements delineated here. Using TADA⁺, 102 genes with q-value less than 0.1 are identified, including three genes that have excessive PTVs in siblings (EIF3G, KDM5B, RAI1). By contrast, TADA^O identifies only 79 genes when applied to the same data. Clearly, the new relevant functional information embodied in the pLI and MPC scores improves the power of TADA by refining the model.

Simulations to evaluate TADA⁺

Simulations illustrate the performance of TADA⁺ when applied to de novo mutations only. In this setting, we simulate three types of de novo variants: PTV, MisA, and MisB, using the mean risks and mutation rates from real data. Below is the detailed procedure.

1. Randomly select 5% of 17,484 autosomal protein-coding genes as the signal genes; denote the set of signal genes as G_S and the null genes as G_N.

2. For each signal gene g∈G_S, generate risk γ_g for each three types of variants from a Gamma distribution, ${\gamma }_g^a\sim Gamma\left({\overline{\gamma }}_g^a,\beta \right),$, a = (PTV,MisA,MisB), where β = 0.2 and the hyperparameters ${\overline{\gamma }}_g^a$s are set to match the empirical counts. Note that ${\overline{\gamma }}_g^{MisA}$ and ${\overline{\gamma }}_g^{MisB}$ are the same across all genes, but ${\overline{\gamma }}_g^{PTV}$ are different.

3. For the null genes g∈G_N, set ${\gamma }_g^{PTV}={\gamma }_g^{MisA}={\gamma }_g^{MisB}=1.$.

4. For each variant, generate the counts from a Multinomial distribution, where the total number is the expected total counts $2N\sum _g{\mu }_g^a{\gamma }_g^a,$, and the probability is proportional to ${\left\{{\mu }_g^a{\gamma }_g^a\right\}}_{g=1}^M.$. The mutation rates are taken from the real data.

5. Apply TADA⁺ with Bayes Factors having a lower limit (floor) of 1, and calculate the empirical FDR.

6. Repeat steps 1-5 one hundred times.

Figure S2L (original BF) and Figure S2M (floor BF) show that the TADA⁺ model controls FDR. Applying the floor principle increases the FDR by a modest amount. In practice we found that there was considerable heterogeneity across genes and this adjustment was necessary.

TADA^O versus TADA⁺ analyses

We explore the performance of TADA^O and TADA⁺ with four analyses:

1. TADA^O applied to the previous ASC cohort (ASC2015), de novo variants only.

2. TADA^O applied to the new ASC cohort (ASC2018), de novo variants only.

3. TADA⁺ applied to ASC2018, de novo variants only.

4. TADA⁺ applied to ASC2018, de novo and case-control variants.

By moving through the four analyses, we change one variable at a time and analyze the consequences. From A to B, we evaluate the impact of the new de novo data introduced as part of ASC2018. From B to C, we compare the improvements in the model by contrasting TADA^O and TADA⁺. From C to D, we assess the impact of adding in the case-control data.

With additional data and a more powerful TADA model, we obtain substantial new discoveries. We identify 31 genes in A, 65 genes in B, 85 genes in C and 102 genes in D. Contrasting genes discovered in A with the new ones discovered in B, we compare the mutation rates and find that the newly discovered genes are 8.9% smaller for PTV (Wilcoxon test p value = 0.35) and 5.8% smaller for Mis3 (Wilcoxon test p value = 0.47) on average; likewise we find that the average fraction of Mis3 over all de novo mutations (Mis3 + PTV) is 0.04 larger (Wilcoxon test p value = 0.63). The similarity in mutation rate and types of mutations found in the newly discovered genes suggests that they are primarily due to the larger sample size. The additional genes discovered in C are due to the more powerful TADA model.

Evaluating the q-valuesfrom these analyses—for the genes with a q-value less than 0.1 in at least one analysis—q-values typically decrease in sequence from analysis A to B to C to D (Figure S2N, showing B as “TADA^O, dn,” C as “TADA⁺, dn,” and D as “TADA⁺, dncc”), with the q-value of analysis D being the smallest. Of the genes with a q-value greater than 0.1 in D but less than 0.1 in at least one other analysis, most are downgraded in analysis D because of refinements in the new TADA model (with the genes or variants having, for instance, low pLI score or low MPC score, particularly MPC less than 1 or missing and thus not categorized as MisA or MisB). A Manhattan plot of the 102 genes identified in D is shown in Figure 2.

ASD_P, ASD_NDD and DDD gene heterogeneity analyses

Heterogeneity analyses were performed using a chi-square approximation test and a Fisher’s exact test (FET) based on de novo counts in ASD and neurodevelopmental delay (NDD) for different subsets of genes. Variants were counted if they were disruptive, i.e., a protein-truncating variant or a missense variant with MPC score ≥ 1. Variant counts in ASD (“dn ASD”) were based on this study, while variant counts in NDD (“dn NDD”) were based on 5,264 trios ascertained for severe NDD (Table S4).

We started out with the list of 102 TADA ASD genes, which we classified as either ASD_P or ASD_NDD (Figure 4). We also considered the 49 ASD_NDD genes and the 102 TADA genes in combination with an “NDD set” of genes containing disruptive variants in the 5,264 NDD trios (avoiding double-counting of genes disrupted in both ASD and NDD). A table of these genes is provided below.

Gene set	# genes	dn ASD	dn NDD
TADA 102	102	391	514
ASDP	53	176	43
ASDNDD	49	215	471
ASDNDD (including NDD set)	90	258	825
All (including NDD set)	143	434	868

For the 102 TADA ASD genes, we can evaluate whether the count of disruptive de novo events is homogeneous for the ASC (“dn ASD”) versus NDD (“dn NDD”) samples: the answer is no (p = 5 × 10⁻¹²), the data are highly heterogeneous. If we consider the ASD_P and ASD_NDD genes by themselves, however, neither subsample shows significant heterogeneity. We can also include the NDD gene set, bringing the overall total to 143 (eliminates genes on chromosome X and FOXG1; NUP155 was eliminated in the previous analysis, due to a lack of de novo mutations). With this expanded list, heterogeneity naturally increases (p = 4 × 10⁻²⁶). If we reasonably put the newly added genes into the ASD_NDD list, we find that there is now heterogeneity in this set (p = 0.001), and it is driven by the lack of mutations in ASD subjects for the newly added NDD genes (see below).

		P-value
Gene set	# genes	Chi-square approximation	FET1
TADA 102	102	5.1 × 10−12	5.5 × 10−9
ASDP	53	0.971	0.916
ASDNDD	49	0.389	0.259
ASDNDD (including NDD set)	90	0.001	0.004
All genes (including NDD set)	143	4.3 × 10−26	3.2 × 10−24

¹Average over 100 repetitions

Because of the total counts involved in the analyses, the FET was performed in independent (random) subsets and then the statistics were combined, and results represent the average over 100 repetitions. For the chi-square test, the genes were required to have at least one de novo event in either ASD or DDD. This removed 1 ASD_P gene from the analysis.

Genes in Recurrent Genomic Disorders (GD)

Curation of reported GD loci

We constructed a list of genomic loci previously reported to be associated with ASD- or NDD-related phenotypes due to rare copy number variants (CNVs). We first collated coordinates of pathogenic “genomic disorder” (GD) regions as reported by nine previous studies (Sanders et al., 2015; Cooper et al., 2011; Wapner et al., 2012; Schaefer et al., 2013; Dittwald et al., 2013; Coe et al., 2014; Pinto et al., 2010; Wright et al., 2015; Rehm et al., 2015) and converted all coordinates to human reference genome build GRCh37/ hg19 with the UCSC liftOver tool, as necessary. We next clustered the coordinates of all overlapping CNV regions using svtk bed-cluster and a minimum 50% reciprocal overlap between segments, retaining the median clustered coordinates of all CNV regions appearing in at least two of the nine studies considered. After clustering, we excluded any CNV segments > 5Mb in size and all segments on sex chromosomes. Finally, we annotated each CNV segment passing all filters with all overlapping genes drawn from the list of 17,484 autosomal protein-coding genes considered during TADA analyses.

Assessment of overlap between ASD-associated genes and GD loci

We designed three permutation-based approaches to benchmark null expectations for the overlap of ASD-associated genes and GD loci. All approaches involved randomly drawing new sets of collinear genes for each GD locus from the list of all 17,484 autosomal protein-coding genes considered in TADA analyses, but differed in how these new genes were selected. These sampling approaches are summarized as follows:

1. Matched on number of genes: a new collinear list of genes was drawn for each GD locus, where the number of genes was matched to the number of genes in the original GD locus.

2. Matched on PTV mutation rates: a new collinear list of genes was drawn for each GD, where the number of genes was determined such that the sum of their estimated PTV mutation rates was at least as large as the sum of the estimated PTV mutation rates of the original list of genes in that GD locus.

3. Matched on brain expression, PTV mutation rates, and number of genes: prior to permutation, all genes were assigned a PTV mutation rate quintile and a brain expression quintile determined by the median brain expression value for that gene across all samples and all brain regions present in GTEx release v7 calculated after excluding genes with non-zero median brain expression. During permutation, a new collinear list of genes was drawn for each GD such that the number of genes matched the original GD locus, with the additional requirements that the distribution of these genes across brain expression quintiles and PTV mutation rate quintiles were also preserved.

For each permutation, we performed one of the three above approaches for all 51 GD loci to obtain a new set of sampled genes, and we then counted the number of newly sampled genes that matched the TADA thresholds for ASD association in this study. We performed 1,000,000 permutations for each approach and computed p values based on the fraction of all permutations where the number of GD loci with at least one randomly sampled ASD-associated gene matched or exceed the empirical observation in the original data. Fold-changes (FCs) were determined as the observed number of GD loci with at least one ASD-associated gene divided by the mean number of GDs with at least one ASD-associated gene across all 1,000,000 permutations.

Finally, we titrated additional parameters to examine the variability of results from this permutation approach. For each of the three gene-sampling schemes above, we performed a separate 1,000,000 independent permutations for each combination of two additional factors, as follows:

1. ASD-associated gene list: we considered two different significance levels for ASD-associated genes: 102 genes identified with TADA⁺ (FDR ≤ 0.1) and 26 genes identified as reaching Bonferroni-corrected significance (Table S2).

2. Chromosome sampling weights: for each GD locus in each permutation, an autosomal chromosome was selected based on one of two weighting schemes prior to randomly sampling a new set of collinear genes. These weights were either (1) determined by the fraction of all autosomal genes located on each chromosome, or (2) determined by the fraction of GD loci located on each chromosome.

All results were consistent across gene sampling strategies and the additional parameters had limited influence on our individual results or overall conclusions (Figure 3).

Enrichment of Common Variants in the Detected Genes

To investigate whether the 102 ASD-associated genes were enriched for common variants associated with ASD and genetically correlated traits, we ran competitive gene-set enrichment analyses on the set of 102 genes using MAGMA (de Leeuw et al., 2015) with brain-expressed genes from BrainSpan (see section below on developmental expression data) as background. We used summary statistics from the latest GWAS of ASD (Grove et al., 2019), ADHD (Demontis et al., 2019), major depression without the 23andMe contribution (Wray et al., 2018), schizophrenia (Schizophrenia Working Group of the Psychiatric Genomics Consortium, 2014), and educational attainment (Lee et al., 2018), as well as a GWAS of height (Wood et al., 2014) as a control. In addition, to illustrate the effect of statistical power in the GWAS, we ran enrichment analyses also for historical GWAS for these phenotypes (Neale et al., 2010; Ripke et al., 2011, 2013a, 2013b; Rietveld et al., 2013; Okbay et al., 2016). From the summary statistics, gene-based p values were estimated using test statistics defined as the sum of −log₁₀(SNP p values) for SNPs located within the transcribed region plus a padding of 10kb flanking regions on either side. The gene-set enrichment was conducted by regressing gene-based Z-scores on a dichotomous gene-set indicator and covariates, which included gene size, gene density, sample size, the reciprocal of the minimal allele count, and the logarithm of these variables. We applied the default settings in MAGMA (Figure 3).

Defining Gene Groups

Past analyses have identified two major groups of ASD-associated genes: those involved in gene expression regulation (GER) and those involved in neuronal communication (NC) (De Rubeis et al., 2014; Sanders et al., 2015). A simple gene ontology analysis with our list of 102 ASD genes replicates this finding, identifying 16 genes in category GO:0006357 “regulation of transcription from RNA polymerase II promoter” (5.7-fold enrichment, FDR = 6.2x10⁻⁶) and 9 genes in category GO:0007268: “synaptic transmission” (5.0-fold enrichment, FDR = 3.8x10⁻³). To assign genes to the GER and NC categories, we used a combination of gene ontology, gene descriptions, and primary research.

Fifty-eight genes were assigned to the GER group based on one of:

1. Clear description of a role as a chromatin modifier, transcription factor, or DNA/RNA binding protein on RefSeq (O’Leary et al., 2016).

2. Evidence of role as a chromatin modifier, transcription factor, or DNA/RNA binding protein in primary research identified on PubMed (https://www.ncbi.nlm.nih.gov/pubmed).

3. Located in the nucleus (GO:0005634) and annotated with at least two of the following gene ontology groups or their children:

   • GO:0000122:negative regulation of transcription by RNA polymerase II
   • GO:0000785:chromatin
   • GO:0000981:RNA polymerase II transcription factor activity, sequence-specific DNA binding
   • GO:0000988:transcription factor activity, protein binding
   • GO:0003682:chromatin binding
   • GO:0003700:DNA-binding transcription factor activity
   • GO:0006325:chromatin organization
   • GO:0010468:regulation of gene expression
   • GO:0045944:positive regulation of transcription by RNA polymerase II

Twenty-four genes were assigned to the GER group based on one of:

1. Clear description of a role in the synapse or regulating membrane potential on RefSeq (O’Leary et al., 2016).

2. Evidence of a role in the synapse or regulating membrane potential in primary research identified on PubMed (https://www.ncbi.nlm.nih.gov/pubmed).

3. Located in the cytoplasm (GO:0005737) and annotated with at least two of the following gene ontology groups or their children:

   • GO:0007267:cell-cell signaling
   • GO:0042391:regulation of membrane potential
   • GO:0045202:synapse

Of the remaining 20 genes, 9 are annotated with GO:0007010:cytoskeleton organization or child terms of this ontology term; these genes are classified as “Cytoskeleton genes.” The remaining 11 genes are described as “Other.” See Table S4 and Figure 4.

Comorbid Phenotypes

Full-scale IQ scores were measured using several tests including, but not limited to, the Differential Ability Scales, Second Edition (Elliott, 2007); the Mullen Scales of Early Learning (Mullen, 1995); the Wechsler Intelligence Scale for Children (Wechsler, 1992); and the Wechsler Abbreviated Scale of Intelligence (Wechsler, 1999). The full-scale IQ estimates were taken from the full-scale deviation IQ variable when available and full-scale ratio IQ when it was not (Chaste et al., 2015). Full-scale IQ is normally distributed with a mean of 100 and a standard deviation of 15, by definition. We defined intellectual disability to be if a subject met one of the following conditions: a full-scale IQ (FSIQ) < 70 (i.e., two standard deviations below the mean), if the proband was administered but could not complete an IQ test, indicated by the subject having a date for their IQ test but no IQ score, or if the subject had a human phenotype ontology (HPO) term or International Classification of Diseases (ICD) code indicating intellectual disability or mental retardation. Age of walking unaided (in months) was taken from question 5A from the Autism Diagnostic Interview (ADI) (Lord et al., 1994). We divided individuals into three possible categories for seizure status: yes, no, and unknown. A subject was put into the yes bin if he or she had a diagnosis of seizures or epilepsy, or a value of 2 on question 85 from the ADI (indicating a diagnosis of epilepsy). A subject was put into the no bin if no seizure/epilepsy diagnosis was indicated or if ADI question 85 had a value of 0. All remaining subjects were put into the unknown bin (Figure 4).

Burden of mutations in ASD as a function of IQ and additional comorbid phenotypes

Burden of mutations over all genes.

We used full-scale IQ to separate subjects into groups. Of the 5,298 probands with any de novo variant, 3,010 have FSIQ information; of these, 2,055 (68.3%) have a FSIQ > 70 and 1,586 (52.7%) have a FSIQ > 82. For a sample size N, the expected number of mutations within genes is computed as E = 2Nø, where ø is the sum of the mutation rate, per variant type, over all relevant genes. (For example, to calculate ø for PTVs in genes with pLI > 0.995, we compute the sum of the PTV mutation rates for these genes.) We then compare E to the observed count for this mutation class, O, and evaluate the distribution of O/E as a chi-square statistic with 1 degree of freedom.

Burden of mutations over 102 TADA ASD genes.

This analysis addresses the question of whether the signal found in the 102 genes with q < 0.1 could have arisen solely from low IQ subjects, such that any mutations found in higher IQ subjects occurred by chance. To answer this question, we must address the bias inherent in choosing 102 genes because they have q < 0.1. To do so, we performed model-based simulations, similar to those used to evaluate the properties of the TADA model. We first select 874 genes with the smallest q-values from the real data and label them “signal genes.” Let M = 0.306N be the number of subjects with IQ < 70 (as seen above) who accumulate mutations at rates greater than chance. We generate mutations for the signal genes using the TADA model and Poisson rate (2Mγμ), where μ is the gene-specific mutation rate and γ is the increased rate of mutations due to this being a risk gene and the mutation of a particular type, and we generate additional mutations at a Poisson rate 2[N – M]μ. We generate mutations in non-signal genes at a Poisson rate (2Nμ). We run TADA to get the new top 102 genes and the new signal genes, and we record counts occurring in new signal genes by chance (i.e., for individuals with high IQ). We perform the simulation 500 times to obtain the distribution of counts in signal genes for individuals with high IQ and compare this to the observed data. We then repeat the analysis, splitting on an IQ of 82 instead of 70.

For all four informative de novo mutation types (two missense categories and two PTV categories), the expected counts were consistently lower than the observed count; only for missense mutations with MPC between 1 and 2 does the expected count, 13.54 (±4.2) approach the observed value, 23 (p = 0.03). For all other mutation types, the empirical p value is far smaller, based on 500 simulations (MPC ≤ 2: 13.9 ± 3.9 expected versus 28 observed; PTV for pLI ≥ 0.995: 8.3 ± 3.0 versus 48; and PTV for 0.5 ≤ pLI < 0.995: 3.0 ± 1.9 versus 15). We also performed these simulations for a split on IQ at 82 and reached the same conclusion, i.e., that the mutations in the higher IQ ASD subjects accumulate at a rate far greater than chance (e.g., Figure 4).

GER and NC mutations in ASD as a function of age of walking and IQ

As with the ASD_P and ASD_NDD genes (Figure 4), we similarly compared whether ascertained ASD individuals harboring de novo missense (MPC ≥ 1) or de novo PTVs in GER and NC genes differed from one another and the remaining ASD individuals with respect to age of walking and full-scale IQ when such phenotype data was available (4,456 ASD individuals had available age of walking data; 4,821 individuals had available full-scale IQ data). The 140 ASD individuals with these groups of de novo variants in GER genes walked 1.84 months later than the 71 ASD individuals with such de novo variants in NC genes (p = 0.01; 95% CI: 0.37-3.31; two-sided, two-sample t test) and 3.4 months later than the remaining 4,204 ASD individuals (p = 7.54x10^-21; 95% CI: 2.69-4.11; two-sided, two-sample t test) (Figure S3A). Similarly, the 71 ASD individuals harboring de novo missense (MPC ≥ 1) or de novo PTVs in NC genes also walked 1.56 months later than the remaining 4,204 ASD individuals (p = 0.002; 95% CI: 0.59-2.53; two-sided, two-sample t test). A similar trend was also observed with respect to full-scale IQ, although we failed to observe any difference between the 159 ASD individuals with these groups of de novo variants in GER genes and the 77 ASD individuals with such de novo variants in NC genes (p = 0.84; two-sided, two-sample t test). The 159 ASD individuals with de novo missense (MPC ≥ 1) and de novo PTVs in GER genes had a full-scale IQ 15.23 lower (95% CI: 11.02-19.46) than the remaining 4,204 ASD individuals (p= 1.6x10^-12; two-sided, two-sample t test) (Figure S3B). Similarly, the 77 ASD individuals with de novo missense (MPC ≥ 1) and de novo PTVs in NC genes had a full-scale IQ 15.97 lower (95% CI: 9.95-21.99) than the remaining 4,204 ASD individuals (p = 2.1x10^-7; two-sided, two-sample t test).

Expression Analysis

Tissue-specific expression

Genotype-Tissue Expression (GTEx) RNA-seq data (https://www.gtexportal.org/home/) were summarized to GENCODE10 and gene-level reads per kilobase million mapped reads (RPKM) values were used across 53 tissue types, including 13 distinct brain regions. Samples with an RNA integrity number (RIN) ≤ 7 were removed from subsequent analyses. Genes were defined as brain-expressed if they were present at an RPKM of 0.5 in 80% of the samples from at least one tissue type, resulting in 27,546 genes. Finally, expression values were log-transformed (log₂[RPKM+1]).

To determine tissue-specific gene expression signatures (i.e., genes which are significantly more expressed in a given tissue type compared to all other tissues), a linear regression model was applied for each gene for each tissue against all other tissues. Models were adjusted for age, RIN, gender, individual as a repeated-measure, and surrogate variables to account for potential batch effects and other unwanted technical and biological variation. Significance values were adjusted for multiple testing using the Benjamini and Hochberg (BH) method to estimate FDR. After the BH correction, genes with q-value < 0.05 and log₂ FC > 0.5 are defined as “tissue-specific” in a given tissue, though we note that a gene may be listed as tissue-specific in more than one tissue, especially if those tissues are closely related. These curated data formed the basis of our tissue-specific gene set enrichment analysis.

To test for over-representation of tissue-specific expression within a given gene set, a modified version of the GeneOverlap function in R was used, so that all pairwise tests were corrected for multiple testing using the BH method. The Fisher’s exact test function also provides an estimated odds ratio in comparison to a tissue- and genome-wide background set of 27,546 genes.

Developmental neocortex expression

BrainSpan developmental RNA-seq data (http://www.brainspan.org) were summarized to GENCODE10 and gene-level RPKMs were used across 528 samples from 40 individuals (Li et al., 2018). Only the neocortical regions were used in our analysis—dorsolateral prefrontal cortex (DFC), ventrolateral prefrontal cortex (VFC), medial prefrontal cortex (MFC), orbitofrontal cortex (OFC), primary motor cortex (M1C), primary somatosensory cortex (S1C), primary association cortex (A1C), inferior parietal cortex (IPC), superior temporal cortex (STC), inferior temporal cortex (ITC), and primary visual cortex (V1C). Samples with RIN ≤ 7 were removed from subsequent analyses. Genes were defined as expressed if they were present at an RPKM of 0.5 in 80% of the samples from at least one neocortical region at one major temporal epoch, resulting in 22,141 genes across 299 high-quality samples ranging from 8 post-conceptual weeks to 40 years of age (Figure S4A). Finally, expression values were log-transformed (log₂[RPKM+1]).

Linear regression was performed for each of the 22,141 genes, modeling gene expression as a continuous dependent variable, as a function of a binary ‘prenatal’ stage variable. Similar to tissue-specific linear models (as above), each regression analysis included gender, individual as a repeated-measure, ethnicity, and surrogate variables as adjustment variables. The regression model generated a ‘prenatal effect’ (t-statistic) of the log₂ FC of prenatal versus postnatal transcript abundance. A BH multiple test correction was used to estimate FDR. Genes were defined as either prenatally or postnatally biased (log₂ FC > 0.1 and q-value < 0.05) or unbiased in expression (q > 0.05). Under this paradigm, we measured the concordance of the prenatal effect across each of the 11 neocortical brain regions against the combination of all 11 areas to ensure consistent gene-based effects; we observed an average r of 0.956. Subsequently, a total of five gene sets (102 ASD genes, 53 ASD_P genes, 49 ASD_NDD genes, 58 GER genes, and 24 NC genes) were evaluated by a Wilcoxon signed rank test to determine if the fetal effect distribution of the set differed significantly from the entire neocortical background, using the reduced statistic of one fetal effect per gene. The neocortical background was defined as genes which were simultaneously detected by WES in the current study as well as genes found to be expressed in the neocortex following quality control procedures (described above).

Early developmental neocortical co-expression modules from BrainSpan expression data

Weighted gene co-expression network analysis (WGCNA) was used to build a signed co-expression network from all early developmental samples passing our QC standards (as above). This resulted in 177 high-quality samples ranging from 8 post-conception weeks to 1 year of age that were used to build an early developmental network. The absolute values of the biweight midcorrelation coefficients were computed for all possible gene pairs and resulting values were transformed with an exponential weight (β). We used a β threshold power of 21 so the subsequent network satisfied scale-free topology (R² > 0.8) and had a high mean connectivity and sufficient information for module detection.

Module robustness was ensured by randomly sampling (2/3 of the total) from the initial set of samples 1000 times followed by consensus network analysis to define modules. The dynamic tree-cut algorithm was used to detect network modules with a minimum module size set to 200 and a cut tree height set to 0.9999. Singular value decomposition of each module’s expression matrix was performed and the resulting module eigengene (ME), equivalent to the first principal component, was used to represent the overall expression profile for each module per sample. Pairs of modules were merged when the correlation of their ME values exceeded 0.90. A total of 27 early developmental neocortical co-expression modules were identified. Each module was assessed for over-representation of five gene sets (102 ASD genes, 53 ASD_P genes, 49 ASD_NDD genes, 58 GER genes, and 24 NC genes) using a one-sided Fisher’s exact test and adjusting all pairwise tests for multiple testing using the BH method. Functional annotation of candidate modules was performed using ToppGene (Chen et al., 2009).

Gene expression in cell types from the fetal human neocortex.

To assess cell type enrichment in the developing human cortex, we used data from Nowakowski et al. (2017) consisting of 4,216 cells, which were divided into 25 cell type clusters and expressed 58,865 identified genes. We excluded genes that were not on the list of 17,484 autosomal protein-coding genes used for the TADA analysis, resulting in 17,116 genes which included all 102 TADA ASD-associated genes. The 4,261 cells were divided into 17 bins by developmental stage, measured in post-conception weeks (Nowakowski et al., 2017). For each of the 17 developmental stages, a gene was considered expressed if at least one transcript mapped to this gene in 25% or more of cells for at least one post-conception weeks stage.

For cell type-specific analyses, six cell type clusters were excluded because they could not be unambiguously associated with a cell type. The 19 remaining cell types contained 3,839 cells. Within each cell type cluster, a gene was considered expressed if one or more of its transcripts were detected in 25% or more cells, which resulted in 7,867 protein-coding genes being expressed in one or more cell type cluster.

To determine enrichment for expression of the 102 TADA ASD genes, the universe of genes expressed was determined by the cells in this experiment; e.g., for the cell type-specific enrichment, the universe was U = 7,867 genes. The counts of the two-by-two table for enrichment of ASD genes, by cell type cluster, were: X, the number of TADA genes expressed in the cell type; Y, the number of TADA genes not expressed in the cell type; Z, the total number of genes expressed in the cell type minus X; and U – (X+Y+Z). Given this table, the enrichment odds ratio was calculated and significance judged by Fisher’s exact test.

To evaluate how well cell types clustered, we first found 10% of genes showing the largest variation among cell types, as judged by analysis of variance. Performing hierarchical clustering using dissimilarity of expression for these genes revealed commonalities about the common types of cells (hclust package from R, centroid method) (Figure 5).

To evaluate whether the enrichment odds ratio was a function of the number of genes expressed per cell type, we used linear regression. Because the odds ratio decreases as the number of genes increases, we next asked what might cause this phenomenon. It is reasonable to conjecture that the diversity of genes expressed (i.e., captured in our sequenced transcripts) would likely be a function of the evenness of expression of observed transcripts. In other words, if some transcripts were expressed at high levels, they will tend to lower the chance of capturing other genes in the sequence run for the cell, because the number of reads per cell was limited to fall between 1 and 2 million reads. This relative evenness should be captured by the mean expression over genes, and it is for these data: there is a very strong relationship between mean expression, taken over all expressed genes per cell type, and the number of genes expressed (R² = 94.5%, Figure 5).

Weighted gene co-expression network analysis of BrainSpan bulk cortex gene expression.

To interpret gene co-expression and enrichment across a broader range of early developmental samples, we used Weighted Gene Coexpression Network Analysis (WGCNA) to assess spatiotemporal co-expression from 177 high-quality BrainSpan samples aged 8 pcw to 1 year. WGCNA yielded 27 early developmental co-expression modules, two of which show significant over-representation of 101 ASD genes (PAX5 went undetected in the BrainSpan data and so was not considered) after correction for multiple testing (Figure S4; Table S5): M4 for the NC gene set (∩ = 5 genes, OR = 13.7, p = 0.002, FET); and M25 for all 101 ASD genes (∩ = 17 genes, OR = 12.1, p = 3x10⁻¹¹, FET), although driven by the GER gene set (∩ = 17 genes, OR = 26.2, p = 9x10⁻¹⁶, FET). With regard to single-cell gene expression, genes in the NC-specific M4 showed greatest enrichment in maturing neurons, both excitatory and inhibitory (p < 0.001 for each of 6 neuronal cell types, FET), whereas genes in M25 showed enrichment across all 19 cell types (p < 0.001 for all cell types, FET). The DAWN associated genes are enriched in M3 (∩ = 10, OR = 10.1, p = 5x10⁻⁶, FET) and M25 (∩ = 7, OR = 5.9, p = 0.004, FET) but not M4, although expression of genes in M4 are highly correlated with those of M3 during early development, and both are highly expressed prenatally. Comparing our gene modules to previously published candidate ASD gene networks obtained using WGCNA (Parikshak et al., 2013) shows that our M4 strongly overlaps with previously identified M16 (p = 5.5x10⁻⁶⁹, FET), and our M24 overlaps with previously identified M2 (p = 1.3x10⁻²³⁹, FET) (note that both studies make use of BrainSpan data so the overlap is not unexpected but does help to relate the results from the two studies).

Detecting Association with Networks (DAWN)

Extended gene discovery with co-expression data

The DAWN (Detecting Association With Networks) algorithm is a network-based gene discovery algorithm. The main assumption of the algorithm, related to this research, is that ASD-related genes are working as a functional group and should be co-expressed in a relevant spatio-temporal window during neurodevelopment. The algorithm predicts ASD-related genes using their interactions with other genes in the gene partial co-expression network, which is constructed using a Partial Neighborhood Selection method. A hidden Markov random field model assigns network-adjusted posterior risk scores to each gene (Liu et al., 2014; Liu et al., 2015). A gene is assigned a higher posterior risk score if the gene (1) has a high prior risk assigned using exome sequencing studies (i.e., TADA) and (2) is highly interacting with other risk genes.

To estimate the partial co-expression network, we used the BrainSpan microarray dataset (https://developinghumanbrain.org/; Kang et al., 2011). We opted for this dataset over the RNA-seq from an overlapping group of samples (Li et al., 2018) due to the larger number of samples and individuals in the microarray data. We extracted the subset of the data for a spatio-temporal window that was previously implicated for ASD risk: midfetal development in the prefrontal cortex (PFC) (Willsey et al., 2013). Because the microarray probes for CHD8, one of the genes with the lowest p values for ASD association (De Rubeis et al., 2014), do not perform well (Willsey et al., 2013; Cotney et al., 2015), we elected to impute the expression of CHD8 in microarray data from the RNA-seq data. To do so, we picked the top genes that are highly correlated with CHD8 in the RNA-seq data. Using the multivariate normal data imputation method, we imputed the corresponding measurements of CHD8 in the microarray data for DAWN analysis. We input the TADA p values as the prior risk scores. DAWN works with p values less than, but not equal to, 1.0. Thus, we replaced the p values of 7,994 genes (45.7% of total genes) with a p value equal to 1.0 with 0.999. We fixed the top 10 ASD-associated genes with respect to TADA q-values as seed genes in the program. No additional covariates were supplied. The input hyperparameters for the DAWN algorithm were lambda = 0.24, p value cutoff = 0.1, and partial correlation threshold = 0.7. DAWN yielded 138 genes (FDR ≤ 0.005), including 83 genes that are not captured by TADA, with 69 of these 83 correlated with many other genes (Table S5). Of the 83, 19 are implicated in neurodevelopmental disorders, and seven of these have autosomal recessive inheritance (Table S5). Of the 138 genes, 38 are expressed in excitatory cell types (p < 1.6x10-4, FET), 25 are also expressed in inhibitory cell types (p < 7.9 × 10-4, FET), and many play a role in GER or NC.

Assessment of interactions by gene function

We used the DAWN results for a downstream network analysis of the interactions between synaptic genes and chromatin genes on a network of (1) ASD risk genes and (2) additional genes chosen by DAWN as tightly interacting with ASD risk genes. The list of synaptic genes was obtained from Genes to Cognition (http://www.genes2cognition.org/db/GeneList). Specifically, we used lists L09-L16, which include the human orthologs of various synaptic complexes in mouse (1,123 genes). The list of chromatin modifiers was obtained from the HIstome Database (http://www.actrec.gov.in/histome/; Khare et al., 2012; Huang et al., 2013; 173 genes total). We picked a threshold of FDR < 0.025, which yielded 100 genes in a DAWN ranking and evaluated interactions among them to form our subnetwork. Of these 100 genes, 40 genes have a TADA q-value < 0.1.

Protein-Protein Connectivity Among ASD Genes

We used the InWeb_IM (Li et al., 2017) database of direct protein-protein interactions (PPI) to investigate whether the number of connections among ASD_P and ASD_NDD genes exceeds expectation, suggesting significant functional relatedness. All candidate genes were brain-expressed as confirmed by the Allen Human Brain Atlas RNA-sequencing data (http://portal.brain-map.org/), as this could otherwise serve as a potential confounding factor for excessive connectivity, compared to the general pool of genes present in the reference PPI network. We binned genes in each tested gene list into deciles of mean brain expression (in TPM) and used this distribution as a further reference for construction of random gene lists for significance analysis. To assess the significance of observed connectivity within each candidate gene list, we performed 1000 random draws of gene sets matching the candidate gene list in number of genes and distribution of expression levels. Empirical p values were estimated as the proportion of random gene sets with greater or equal connectivity compared to the candidate gene list. Subsequently, to estimate the significance of connections with a known list of genes associated with neurodevelopmental delay (Kosmicki et al., 2017), we performed 1000 random draws of gene sets matching the candidate gene lists in number of genes and brain expression distribution. Further, the number of direct connections was estimated between a random gene set and neurodevelopmental delay-associated genes. Empirical p values were estimated as the proportion of random gene sets with a greater or equal number of connections to neurodevelopmental delay-associated genes compared to the candidate gene list.

To explore whether GER and NC gene sets interact more than would be expected by chance, we analyzed protein-protein interaction (PPI) networks (Figure S5B; Table S5) and found they do not: there was a significant excess of interactions among all ASD genes (82 genes, p = 0.02, FET), GER genes (49 genes, p = 0.006, FET), and NC genes (12 genes, p = 0.03, FET), but not among GER and NC genes (2 genes, p = 1.00, FET). Nor do GER genes regulate the NC genes, according to our analyses, although GER-GER regulation was enriched (Figure S5C; Table S5).

Enrichment of Transcription Factor Regulatory Networks for GER Genes

Starting with the 58 GER genes, we performed a systematic search for regulatory targets identified by protein-DNA interactions (e.g., ChIP-Seq) or protein-RNA interactions (e.g., iCLIP). First, we searched for target sets in available databases: ChEA (Lachmann et al., 2010) and ENCODE (Birney et al., 2007). The target lists were obtained from the Enrichr libraries (ChEA 2016 and ENCODE ChIP-seq 2015; Chen et al., 2013) and from a literature search for available ChIP or CLIP experiments, which are immunoprecipitation-based techniques to identify protein interactions with DNA and RNA, respectively. We found target data for 26 of 55 GER genes, with targets ranging from 5 to 8,189 per gene. The data were generated in a wide range of tissues ranging from cell lines to liver to cortex and stemmed from 2 species (mouse and human). In total, we identified 21,514 gene targets from the 26 genes, which included 14,925 protein-coding genes from Ensembl. We constructed a network of 48,932 interactions with genes as the nodes and directed edges as transcription factor regulation relationships (Table S5).

To assess the significance of the connection between GER genes and a set of targets (i.e., NC genes), we generated random gene sets that matched genes with respect to brain expression, de novo PTV mutation rate, and pLI. For mutation rate, we used 5 bins such that each bin contained an equal number of genes (~3,497). For pLI, we split genes into 3 groups: 0 to < 0.5, ≥ 0.5 to < 0.995, and ≥ 0.995 to 1. They contained 12,152, 4,506, and 1,583 genes, respectively.

First, we checked whether GER genes are significantly connected to ASD-associated genes. There are 409 connections between 58 GER genes and the 102 ASD-associated genes (which include the 58 GER genes). Eight self-loops (a protein binding near to the gene that encodes it) were ignored. We generated 1,000 random gene sets of size 102. While the expected number of connections was 314, GER genes have 361 links to ASD-associated genes (p = 0.006). Then, we checked the significance of the connectivity within GER genes (only GER-GER connections). There are 229 connections within GER genes. Repeating the same analysis, we found the expected number of connections to be 175, demonstrating significant connectivity (p < 0.001). On the other hand, the connectivity between GER genes and NC genes was weaker—there are 132 connections, whereas the expected was 140 (p = 0.72).

As a further control, we checked whether GER genes were significantly connected to congenital heart disease risk genes, which is known to have an overlapping genetic component with ASD (Jin et al., 2017). The list of 253 congenital heart disease risk genes was obtained from Jin et al. (2017). Of the 253 genes, 19 were excluded because they are either not autosomal protein-coding genes and/or lack known mutations rates, as used in our analysis. Specifically, 11 are on chromosome X (HCCS, NSDHL, RBM10, PQBP1, ZIC3, GPC3, BCOR, FLNA, OFD1, COX7B, MID1); 6 have no data in ExAC (DNAH11, C1ORF127, IRX5, GATA6, FOXC2, FOXC1); and 2 are noncoding (RNU4ATAC and RPS17). There are 685 links between GER genes and 234 congenital heart disease genes compared to an expected value of 622 (p = 0.007; genes were matched with respect to pLI and mutation rate, but not brain expression). Thus, despite a strong regulatory relationship existing within GER genes and even between GER genes and congenital heart disease genes, this is missing between GER genes and NC genes, suggesting that these functional circuitries act independently rather than as a coherent unit, which is also seen in our DAWN analysis. We note that many of the ChIP and CLIP datasets were not generated in brain tissue and that NC genes are more likely to be brain-specific than GER genes.

Enrichment of CHD8 targets for the GER genes

To assess whether ASD-associated genes relate to known genome-wide CHD8 binding sites, we tested our previously defined GER and NC gene sets for enrichment with human brain-specific sequences from two independent ChIP-seq studies covering: 1) 3,281 CHD8-binding sites in the human mid-fetal brain at 16-19 post-conception weeks (Cotney et al., 2015); and 2) 6,860 CHD8-binding sites in human neural progenitor cells using the intersection of signal-enriched regions detected by all three CHD8 antibodies used in the study (Sugathan et al., 2014). In order to assess overlap with these binding sites, genomic coordinates were defined as the start and end positions for each GER and NC gene (analogous to gene length). A permutation-based approach with 1,000 random permutations was used to determine statistical significance of the overlap between genomic coordinates for GER and NC genes with CHD8-binding sites using the R package regioneR (Gel et al., 2016).

DATA AND CODE AVAILABILITY

All data generated as part of the ASC is transferred to dbGaP with Study Accession: phs000298.v4.p3. Data generated previously are detailed in Table S1 and in the Key Resources Table. TADA has been previously described (He et al., 2013) and enhancements to TADA are described in detail in the main text and the STAR Methods. DAWN has also been described (Liu et al., 2014).

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
ASC-generated WES sequencing data	This paper	dbGaP Study Accession: phs000298.v4.p3
SFARI-generated WES sequencing data	SFARI	https://www.sfari.org/resource/sfari-base/
iPSYCH-generated WES sequencing data	iPSYCH-Broad consortium	http://ipsych.genome.au.dk/
Human reference genome NCBI build 37, GRCh37	Genome Reference Consortium	http://www.ncbi.nlm.nih.gov/projects/genome/assembly/grc/human/
Exome aggregation consortium (ExAC)	Lek et al., 2016	http://exac.broadinstitute.org/
Genome aggregation database (gnomAD)	Karczewski et al., 2019	https://gnomad.broadinstitute.org/
Deciphering Developmental Disorders (DDD)	Deciphering Developmental Disorders Study, 2017	https://www.ddduk.org/
Genotype-Tissue Expression (GTEx) resource	Battle et al., 2017	https://gtexportal.org/home/
BrainSpan	Li et al., 2018	http://www.brainspan.org/
Single-cell RNA-seq data from developing cortex	Nowakowski et al., 2017	https://cells.ucsc.edu/?ds=cortex-dev
InWeb_IM (protein-protein interaction data)	Li et al., 2017	http://www.lagelab.org/resources/
Software and Algorithms
Genome Analysis Toolkit (GATK)	Van der Auwera et al., 2013	https://software.broadinstitute.org/gatk/
Hail	https://hail.is/	https://github.com/hail-is/hail/
Variant Effect Predictor (VEP)	McLaren et al., 2016	http://grch37.ensembl.org/Homo_sapiens/Tools/VEP
TADA	He et al., 2013	http://www.compgen.pitt.edu/TADA/TADA_guide.html
Gene Ontology (via Panther)	Mi et al., 2019	http://www.pantherdb.org/

Highlights.

• 102 genes implicated in risk for autism spectrum disorder (ASD genes, FDR % 0.1)

• Most are expressed and enriched early in excitatory and inhibitory neuronal lineages

• Most affect synapses or regulate other genes; how these roles dovetail is unknown

• Some ASD genes alter early development broadly, others appear more specific to ASD