Predicting the Landscape of Recombination Using Deep Learning

Abstract

Accurately inferring the genome-wide landscape of recombination rates in natural populations is a central aim in genomics, as patterns of linkage influence everything from genetic mapping to understanding evolutionary history. Here, we describe recombination landscape estimation using recurrent neural networks (ReLERNN), a deep learning method for estimating a genome-wide recombination map that is accurate even with small numbers of pooled or individually sequenced genomes. Rather than use summaries of linkage disequilibrium as its input, ReLERNN takes columns from a genotype alignment, which are then modeled as a sequence across the genome using a recurrent neural network. We demonstrate that ReLERNN improves accuracy and reduces bias relative to existing methods and maintains high accuracy in the face of demographic model misspecification, missing genotype calls, and genome inaccessibility. We apply ReLERNN to natural populations of African Drosophila melanogaster and show that genome-wide recombination landscapes, although largely correlated among populations, exhibit important population-specific differences. Lastly, we connect the inferred patterns of recombination with the frequencies of major inversions segregating in natural Drosophila populations.

Introduction

Recombination plays an essential role in the meiotic production of gametes in most sexual species, and is often required for proper segregation (Nicklas 1974) and pairing of homologous chromosomes (reviewed in Zickler and Kleckner 2015). During prophase of meiosis, recombination is initiated by the formation of double-strand breaks across a wide array of organisms (Lichten 2001). A subset of these double-strand breaks will be repaired as crossover events, leading to reciprocal exchange between homologs. Those that are not resolved as crossovers are repaired through a number of mechanisms included noncrossover gene conversions and nonhomologous end joining (Do et al. 2014). Recombination not only plays a central role in meiosis but also has wide-ranging effects on both evolutionary and population genomics (Lewontin and Kojima 1960; Hill and Robertson 1966; Ohta and Kimura 1969, 1970; Smith and Haigh 1974).

Indeed, the population recombination rate, $\rho =4Nr$, is a central parameter in population and statistical genetics (reviewed in Hahn 2018), as at equilibrium, we expect ρ to be proportional to the scale of linkage disequilibrium (LD) in a given region of the genome (Ohta and Kimura 1969). In regions of the genome where ρ is relatively small, we expect increased levels of LD, and conversely, in genomic compartments with high ρ, we expect little LD. Deviations from expected levels of LD given the local recombination rate can be illustrative of the influence of other evolutionary forces such as selection or migration. For example, selective sweeps are expected to dramatically elevate LD near the target of selection (Parsch et al. 2001; Kim and Nielsen 2004; O’Reilly et al. 2008).

Structural variation itself is expected to modulate the landscape of recombination—herein, the map of per-base recombination rates, r, to genomic positions along the chromosomes. For example, both crossovers and noncrossovers are predicated on the alignment of homologous sequences, and structural rearrangements may directly impact such alignments. Chromosomal inversions, long known to suppress crossing over along a chromosome (Sturtevant 1921), are one of the best studied examples of such structural variation. Inversion polymorphisms have been implicated in diverse evolutionary phenomena including local adaptation (Dobzhansky 1937; Kirkpatrick and Barton 2006; Ayala et al. 2013), reproductive isolation (White 1977; Noor et al. 2001; Rieseberg 2001; Ayala et al. 2013), and the maintenance of meiotic drive complexes (reviewed in Jaenike 2001). As suppressors of recombination, we expect a priori that segregating inversions should show distinct histories of recombination in comparison to standard karyotype chromosomes.

Although recombination plays a central role in meiosis and reproduction, the frequency and distribution of crossovers along the chromosomes are themselves phenotypes that can evolve. Not only is there a long tradition of work demonstrating the conditions under which rates of recombination might change (Fisher 1930; Muller 1932; Charlesworth 1976; Barton 1995; Otto and Barton 1997) but increasingly there is good empirical evidence that such changes do indeed occur in nature (reviewed in Ritz et al. 2017). Importantly, recombination rate variation exists between species, between populations, and between sexes of the same species (males generally having shorter maps than females) (Winckler et al. 2005; Kong et al. 2010; Hinch et al. 2011; Singh et al. 2013). Yet, although there is abundant variation in the rate of recombination within and between taxa, methods for accurately measuring this variation have historically involved painstaking experiments or large pedigrees. Thus, genetics, as a field, seeks ever-improving tools for directly estimating recombination rates from sequence data, without relying on pedigree genotyping or other ancillary information.

Accordingly, there is a rich history of estimating ρ in population genetics, including efforts to obtain minimum bounds on the number of recombination events (Hudson and Kaplan 1985; Wiuf 2002; Myers and Griffiths 2003), method of moments estimators (Hudson 1987; Wakeley 1997), composite likelihood estimators (Hudson 2002; McVean et al. 2002; Chan et al. 2012), and summary likelihood estimators (Wall 2000; Li and Stephens 2003). Recently, supervised machine learning methods for estimating ρ have entered the fray (Lin et al. 2013; Gao et al. 2016) and have proven to be competitive in accuracy with state-of-the-art composite likelihood methods such as LDhat (McVean et al. 2002) or LDhelmet (Chan et al. 2012), often with far less computing effort. These methods, taken en masse, have uncovered interesting biology, for instance, the characterization of recombination hotspots (Myers et al. 2005), and are well suited for large samples of high-quality genome or genotype data.

To this end, we sought to develop a novel method for inferring rates of recombination directly from a sequence alignment through the use of deep learning. In recent years, deep artificial neural networks (ANNs) have produced remarkable performance gains in computer vision (Krizhevsky et al. 2012; Szegedy et al. 2015), speech recognition (Hinton et al. 2012), natural language processing (Sutskever et al. 2014), and data preprocessing tasks such as denoising (Vincent et al. 2008). Perhaps most illustrative of the potential of deep learning is the remarkable success of convolutional neural networks (CNNs; Lecun et al. 1998) on problems in image analysis. For example, prior to the introduction of CNNs to the annual ImageNet Large Scale Visual Recognition Challenge (Krizhevsky et al. 2012), no method had achieved an error rate of <25% on the ImageNet data set. In the years that followed, CNNs succeeded in reducing this error rate <5%, exceeding human accuracy on the same tasks (Russakovsky et al. 2015).

In this study, we focus our efforts on recurrent neural networks (RNNs), a promising network architecture for population genomics, which has proven adept for analyzing sequential data of arbitrary lengths (Graves et al. 2013). Unlike other machine learning methods, deep learning approaches do not require a predefined feature vector. When fed labeled training data (e.g., a set of genotypes simulated under a known recombination rate), these methods algorithmically create their own set of informative statistics that prove most effective for solving the specified problem. By training deep learning networks directly on sequence alignments, we allow the neural network to automatically extract informative features from the data without human supervision. Learning directly from a sequence alignment for population genetic inference has recently been shown to be possible using CNNs (Chan et al. 2018; Flagel et al. 2019; Torada et al. 2019), and as we show below, is also true for RNNs. Moreover, supervised deep learning methods, such as RNNs, can be trained directly on the types of missing data that often beset researchers investigating nonmodel organisms using traditional tools.

Here, we introduce recombination landscape estimation using recurrent neural networks (ReLERNN), an RNN-based method for estimating the genomic map of recombination rates directly from a genotype alignment. We find that ReLERNN is both highly accurate and outperforms competing methods at small sample sizes. We also show that ReLERNN retains its high accuracy in the face of demographic model misspecification, missing genotypes, and genome inaccessibility. Further, we present an extension to ReLERNN that takes as input allele frequencies estimated by pooled sequencing (Pool-seq), making ReLERNN the first software package to directly infer rates of recombination in Pool-seq data. These results suggest that ReLERNN has the potential to fill a much-needed role in the analysis of low-quality or sparse genomic data. We then apply ReLERNN to population genomic data from African samples of Drosophila melanogaster. We demonstrate that the landscape of recombination is largely conserved in this species, yet individual regions of the genome show marked population-specific differences. Finally, we find that chromosomal inversion frequencies directly impact the inferred rate of recombination, and we demonstrate that the role of inversions in suppressing recombination extends far beyond the inversion breakpoints themselves.

Results

ReLERNN: An Accurate Method for Estimating the Genome-Wide Recombination Landscape

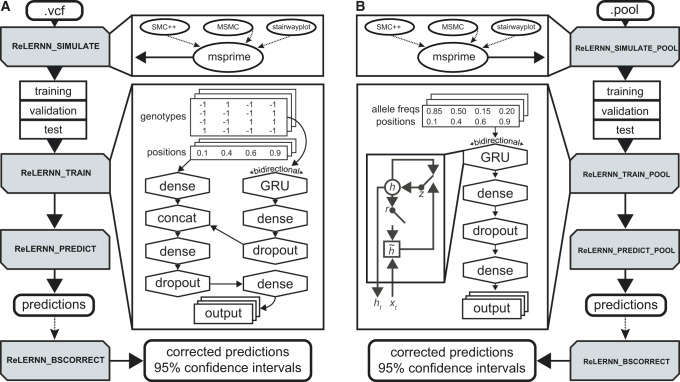
We developed ReLERNN, a new deep learning method for accurately predicting genome-wide per-base recombination rates from as few as four chromosomes. Briefly, ReLERNN provides an end-to-end inferential pipeline for estimating a recombination map from a population sample: it takes as input either a variant call format (VCF) file or, in the case of ReLERNN for Pool-seq data, a vector of allele frequencies and genomic coordinates. ReLERNN then uses the coalescent simulation program, msprime (Kelleher et al. 2016), to simulate training, validation, and test data sets under either constant population size or an inferred population size history. Importantly, these simulations are parameterized to match the distribution of Watterson’s estimator, θ_W, calculated from the empirical samples. ReLERNN trains a specific type of RNN, known as a gated recurrent unit (GRU; Cho et al. 2014), to predict the per-base recombination rate for these simulations, using only the raw genotype matrix and a vector of genomic coordinates for each simulation example (fig. 1 and supplementary figs. S1 and S2, Supplementary Material online). It then uses this trained network to estimate genome-wide per-base recombination rates for empirical samples using a sliding-window approach. ReLERNN can optionally estimate 95% CI around each prediction using a parametric bootstrapping approach, and it uses the predictions generated while bootstrapping to correct for inherent biases in the training process (see Materials and Methods; supplementary fig. S3, Supplementary Material online).

Fig. 1.

A cartoon depicting a typical workflow using ReLERNN’s four modules (shaded boxes) for (A) individually sequenced genomes or (B) pooled sequences. ReLERNN can optionally (dotted lines) utilize output from stairwayplot, SMC++, and MSMC to simulate under a demographic history with msprime. Training inlays show the network architectures used, with the GRU inlay in (B) depicting the gated connections within each hidden unit. Here, r, z, h_t, and $\widetilde{h_{\mathrm{t}}}$ are the reset gate, update gate, activation, and candidate activation, respectively (Cho et al. 2014). The genotype matrix encodes alleles as reference (−1), alternative (1), or padded/missing data (0; not shown). Variant positions are encoded along the real number line (0–1).

A key feature of ReLERNN’s network architecture is the bidirectional GRU layer (fig. 1 and supplementary fig. S1, Supplementary Material online), which allows us to model genomic sequence alignments as a time series. Although feed-forward networks use as input a full block of data for each example, recurrent layers break each genotype alignment into time steps corresponding to discrete genomic coordinates, and iterate over the time steps sequentially. At each time step, the GRUs modulate the flow of information, using reset and update gates that control how the activation is updated (Cho et al. 2014; Chung et al. 2014). This process allows the gradient descent algorithm, known as backpropagation through time, to share parameters across time steps, as well as make inferences based on the ordering of SNPs—that is, to have a spatial memory of allelic associations along the chromosome. The bidirectional attribute of the GRU layer simply means that each example is duplicated and reversed, so the sequence data are analyzed from both directions and then merged by concatenation. We present a generalized GRU for analyzing genomic sequence data, along with a more detailed look at the network architecture parameters used by ReLERNN in supplementary figure S1, Supplementary Material online.

Performance on Simulated Chromosomes

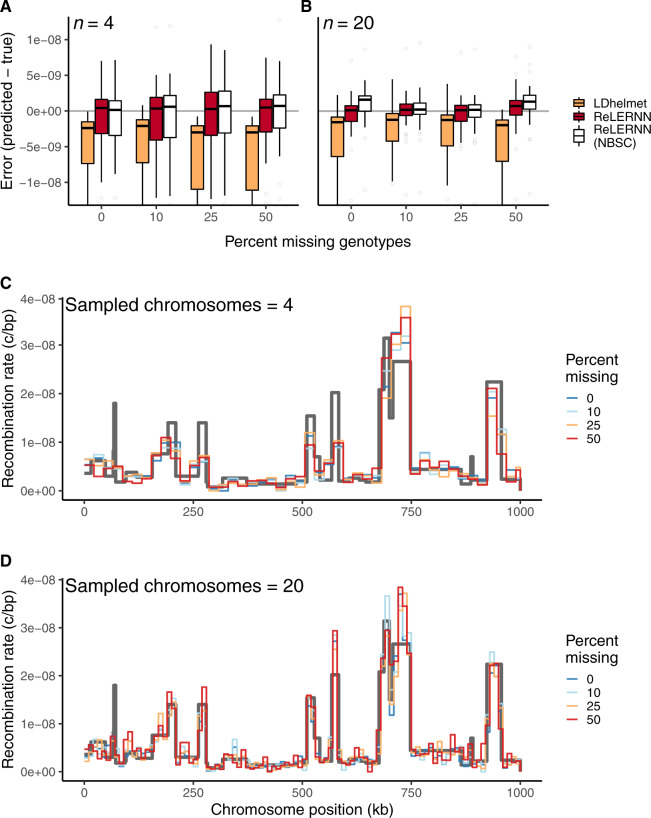
To assess our method, we performed coalescent simulations using msprime (Kelleher et al. 2016), generating whole chromosome samples using a fine-scale genetic map estimated from crosses of D. melanogaster (Comeron et al. 2012). We then used ReLERNN to estimate the landscape of recombination for these simulated examples. ReLERNN is able to predict the landscape of per-base recombination rates to a high degree of accuracy across a wide range of realistic parameter values, assumptions, and sample sizes ($R^2\ge 0.82$; mean absolute error [MAE] $\le 1.28\times {10}^{-8}$). Importantly, the accuracy of ReLERNN is only modestly diminished when comparing predictions based on 20 samples ($R^2=0.93$; $\text{MAE}=3.72\times {10}^{-9}$; fig. 2A) to those based on four samples ($R^2=0.82$; $\text{MAE}=6.66\times {10}^{-9}$; supplementary fig. S4, Supplementary Material online). We also show that ReLERNN performs equally well on phased and unphased genotypes (W = 68.5; P = 0.17; Mann–Whitney U test; supplementary fig. S5, Supplementary Material online), suggesting that any effect of computational phasing error might be mitigated by treating the inputs as unphased variants.

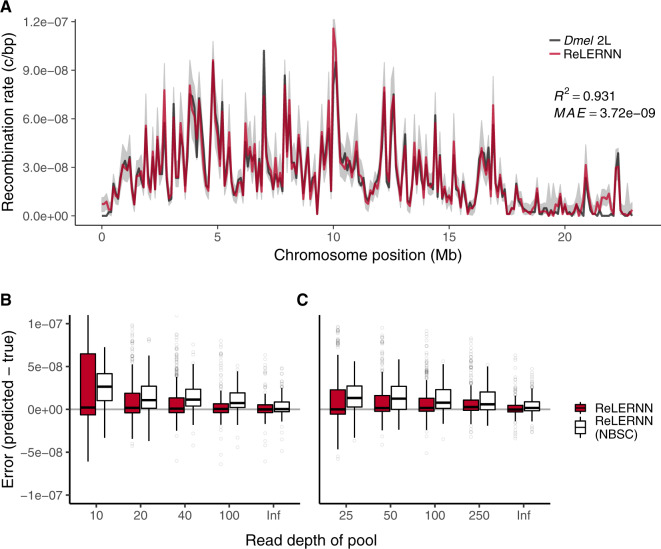
Fig. 2.

(A) Recombination rate predictions for a simulated Drosophila chromosome (black line) using ReLERNN for individually sequenced genomes (red line). The recombination landscape was simulated for n = 20 chromosomes under constant population size using msprime (Kelleher et al. 2016), with per-base crossover rates taken from D. melanogaster chromosome 2L (Comeron et al. 2012). Gray ribbons represent 95% CI. R² is reported for the general linear model of predicted rates on true rates and mean absolute error was calculated across all 100-kb windows. (B) Distribution of raw error ($r_{\text{predicted}}-r_{\text{true}}$) using ReLERNN for Pool-seq data. Pools simulated from the same recombination landscape as above, with n = 20 and (C) n = 50 chromosomes across a range of simulated read depths ($0.5\times$ to 5×; Inf represents infinite simulated sequencing depth). Both the bootstrap-corrected predictions (red) and the nonbootstrap-corrected (NBSC; white) predictions are shown.

Because ReLERNN performed exceedingly well on unphased genotypes, we speculated that it might be able to glean crucial information about recombination rates from a vector of allele frequencies alone. Therefore, we set out to extend ReLERNN to work with Pool-seq data, where the only inputs are a vector of allele frequencies and their corresponding genomic coordinates. Surprisingly, ReLERNN exhibits modest accuracy on simulated Pool-seq data, despite simulated sample and read depths as low as n = 50 and $\text{coverage}=50\times$ ($R^2=0.54$; $\text{MAE}=1.59\times {10}^{-8}$; supplementary fig. S6, Supplementary Material online). Increasing the read depth to a nominal 5×, the sample depth (e.g., n = 50 and $\text{coverage}=250\times$) produced substantially greater accuracy ($R^2=0.69$; $\text{MAE}=1.20\times {10}^{-8}$; supplementary fig. S7, Supplementary Material online). As a general trend, we show that prediction error is reduced by increasing the number of chromosomes sampled in the pool (i.e., increasing allele frequency resolution) and by increasing the depth of sequencing (i.e., reducing sampling error) (fig. 2B). Although there currently exists software for estimating LD in Pool-seq data (Feder et al. 2012), to our knowledge, ReLERNN is the first software to directly estimate rates of recombination using these data.

Although ReLERNN retains accuracy at small sample sizes, it exhibits somewhat greater sensitivity to both the assumed genome-wide average mutation rate, $\overline{\mu }$, and the assumed maximum value for recombination, ρ_max. To assess the degree of sensitivity to these assumptions, we ran ReLERNN on simulated chromosomes assuming $\overline{\mu }$ was both 50% greater and 50% less than the simulated mutation rate, μ_true. In both scenarios, ReLERNN predicts crossover rates that are highly correlated with the true rates ($R^2>0.91$). However, in both scenarios, MAE is inflated but still modest, and the absolute rates of recombination are underpredicted ($R^2=0.91$; $\text{MAE}=1.23\times {10}^{-8}$; supplementary fig. S8, Supplementary Material online) and slightly overpredicted ($R^2=0.94$; $\text{MAE}=1.28\times {10}^{-8}$; supplementary fig. S9, Supplementary Material online) when assuming $\overline{\mu }$ is less than or greater than μ_true, respectively. Moreover, underestimating ρ_max causes ReLERNN to underpredict rates of recombination roughly proportional to the magnitude of the underestimate (supplementary figs. S10 and S11, Supplementary Material online), whereas overestimating ρ_max causes only a minor loss in accuracy ($R^2=0.90$; $\text{MAE}=4.07\times {10}^{-9}$; supplementary fig. S12, Supplementary Material online). Together, these results suggest that ReLERNN is in fact learning information about the ratio of crossovers to mutations, and although ReLERNN is highly robust to errant assumptions when predicting relative recombination rates within a genome, caution must be taken when comparing absolute rates between organisms with large differences in per-base mutation rate estimates or for species. One additional limitation to ReLERNN is its inability to fully resolve narrow recombination rate hotspots (herein defined as $\le 10$-kb genomic regions with $r\ge 50\times$ the genome-wide average). We simulated hotspots of different lengths [$\text{length}\in \{2\hspace{0.17em}\text{kb},4\hspace{0.17em}\text{kb},6\hspace{0.17em}\text{kb},8\hspace{0.17em}\text{kb},10\hspace{0.17em}\text{kb}\},\hspace{0.17em}{r}_{\text{background}}=2.5{\mathrm{e}}^{-9},\hspace{0.17em}{r}_{\text{hotspot}}=1.25{\mathrm{e}}^{-7}$] and found that errors at hotspots were negatively correlated with hotspot length (supplementary fig. S13, Supplementary Material online), suggesting that signal for crossovers at hotspots is being swamped by the background rate within the focal window, especially for very narrow hotspots relative to the focal window. This limitation could be of particular importance when attempting to resolve hotspots in human data, where lengths are often between 1 and 2 kb (Jeffreys et al. 2001; Jeffreys and May 2004).

ReLERNN Compares Favorably to Competing Methods, Especially for Small Sample Sizes and under Model Misspecification

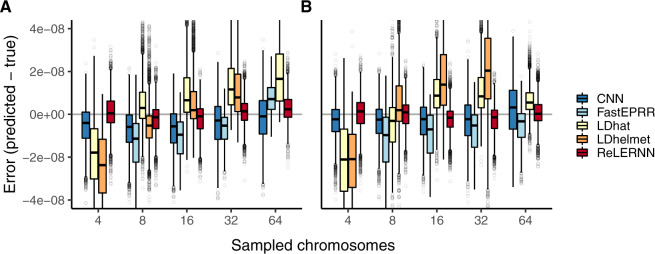
To assess the accuracy of ReLERNN relative to existing methods, we took a comparative approach, whereby we made predictions on the same set of simulated test chromosomes using methods that differ broadly in their approaches. Specifically, we chose to compare ReLERNN against two types of machine learning methods—a boosted regression method, FastEPRR (Gao et al. 2016), and a CNN recently described in Flagel et al. (2019)—and both LDhat (McVean et al. 2002) and LDhelmet (Chan et al. 2012), two widely cited approximate-likelihood methods. We independently simulated 10⁵ chromosomes using msprime (Kelleher et al. 2016) [parameters: $\mathit{sample}\_\mathit{size}\in \{4,8,16,32,64\},\hspace{0.17em}\mathit{recombination}\_\mathit{rate}=U(0.0,6.25{\mathrm{e}}^{-8}),\hspace{0.17em}\mathit{mutation}\_\mathit{rate}=U(1.875{\mathrm{e}}^{-8},3.125{\mathrm{e}}^{-8}),\hspace{0.17em}\mathit{length}=3e^5$]. Half of these were simulated under demographic equilibrium and half were simulated under a realistic demographic model (based on the out-of-Africa expansion of European humans; see Materials and Methods). We show that ReLERNN outperforms all other methods, exhibiting significantly reduced absolute error ($|r_{\text{predicted}}-r_{\text{true}}|$) under both the demographic model and under equilibrium assumptions ($T\le -31$; $P<{10}^{-16}$; post hoc Welch’s two-sample t-tests for all comparisons; supplementary figs. S14 and S15, Supplementary Material online). ReLERNN also exhibited less bias than likelihood-based methods across a range of sample sizes (fig. 3), although all methods generally performed well at the largest sample size tested (n = 64).

Fig. 3.

(A) Distribution of raw error ($r_{\text{predicted}}-r_{\text{true}}$) for each method across 5,000 simulated chromosomes (1,000 for FastEPRR). Independent simulations were run under a model of population size expansion or (B) demographic equilibrium. Sampled chromosomes indicate the number of independent sequences that were sampled from each msprime (Kelleher et al. 2016) coalescent simulation. LDhelmet was not able be used with n = 64 chromosomes and FastEPRR was not able to be used with n = 4.

We also sought to assess the robustness of ReLERNN to demographic model misspecification, where different generative models are used for simulating the training and test sets—for example, training on assumptions of demographic equilibrium when the test data were generated by a population bottleneck. Methods robust to this type of misspecification are crucial, as the true demographic history of a sample is often unknown and methods used to infer population size histories can disagree or be unreliable (see supplementary fig. S21, Supplementary Material online). Moreover, population size changes alter the landscape of LD across the genome (Slatkin 1994; Rogers 2014), and thus have the potential to reduce accuracy or produce biased recombination rate estimates.

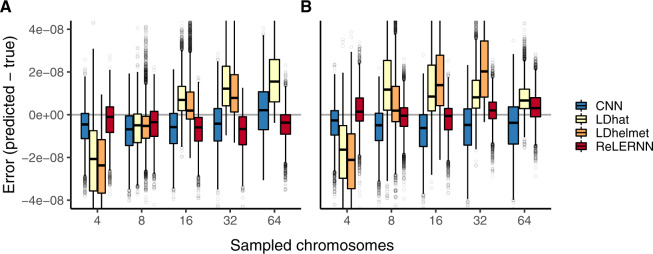
To this end, we trained ReLERNN on examples generated under equilibrium and made predictions on 5,000 chromosomes generated by the human demographic model specified above (and also carried out the reciprocal experiment; fig. 4). We compared ReLERNN with the CNN, LDhat, and LDhelmet, with all methods similarly misspecified (see Materials and Methods). We found that ReLERNN outperforms these methods under nearly all conditions, exhibiting significantly lower absolute error under both directions of demographic model misspecification ($T\le -26$; $P_{\text{WTT}}<{10}^{-16}$ for all comparisons, with the exception of the comparison to LDhelmet using 16 chromosomes; supplementary figs. S16 and S17, Supplementary Material online). We show that the error directly attributed to model misspecification (which we term marginal error; see Materials and Methods) is occasionally higher in ReLERNN relative to other methods, even though ReLERNN exhibited the lowest absolute error among methods. As a prime example of this, we found predictions from LDhelmet were not affected by our misspecification regime at all, but these predictions were still, on an average, less accurate than those made by a misspecified ReLERNN. Interestingly, marginal error is significantly greater when ReLERNN was trained on equilibrium simulations and tested on demographic simulations than under the reciprocal misspecification (T = 26.3; $P_{\text{WTT}}<{10}^{-16}$; supplementary fig. S18, Supplementary Material online). Although this is true, it is important to note that mean marginal error for ReLERNN, in both directions of misspecification and across all sample sizes, never exceeded $3.90\times {10}^{-9}$, suggesting that the additional information gleaned from an informative demographic model is limited.

Fig. 4.

(A) Distribution of raw error ($r_{\text{predicted}}-r_{\text{true}}$) for each method across 5,000 simulated chromosomes after model misspecification. For the CNN and ReLERNN, predictions were made by training on equilibrium simulations while testing on sequences simulated under a model of population size expansion or (B) training on demographic simulations while testing on sequences simulated under equilibrium. For LDhat and LDhelmet, the lookup tables were generated using parameters values that were estimated from simulations where the model was misspecified in the same way as described for the CNN and ReLERNN above. Sampled chromosomes indicate the number of independent sequences that were sampled from each msprime (Kelleher et al. 2016) coalescent simulation. LDhelmet was not able be used with n = 64 chromosomes and the demographic model could not be intentionally misspecified using FastEPRR.

In addition to model misspecification, differences in the ratio of homologous gene conversion events to crossovers can also bias the inference of recombination rates, as conversion tracts break down LD within the prediction window (Przeworski and Wall 2001; Gay et al. 2007). We treated the effect of gene conversion as another form of model misspecification, by training on examples that lacked gene conversion and testing on examples that included gene conversion. As ReLERNN uses msprime for all training simulations, and msprime cannot currently simulate gene conversion, we generated all test set simulations with ms (Hudson 2002). We found that including gene conversion in our simulations biased our predictions, resulting in an overestimate of the true recombination rate (supplementary fig. S19, Supplementary Material online). Moreover, the magnitude of this bias increased with the ratio of gene conversion events to crossovers, $\frac{r_{\text{GC}}}{r_{\text{CO}}}$. As expected, we also observed a similar pattern of bias for LDhelmet, although the magnitude of bias for LDhelmet was less than that exhibited by ReLERNN for $\frac{r_{\text{GC}}}{r_{\text{CO}}}>2$ (T > 4.37; $P_{\text{WTT}}<1.32\times {10}^{-5}$; supplementary fig. S19, Supplementary Material online). As errors in genotype calls can mimic gene conversion—for example, a heterozygous sample being called as a homozygote—filtering low-quality SNP calls, either by removing the individual genotype or by masking sites, has the potential to mitigate gene conversion-induced bias. However, missing genotypes and inaccessible sites have the potential to introduce their own biases, highlighting an area where deep learning methods may have a unique advantage over traditional tools.

ReLERNN Retains High Accuracy on Simulated Low-Quality Genomic Data Sets

Deep learning tools have the potential to perform exceptionally well on poor-quality genomic data sets, such as those with low-quality or low-complexity reference genomes, under sampling regimes where individual samples are at a premium, or where base- and map-quality scores are suspect. This is in part because such attributes of genomic quality can be readily incorporated during training, and deep learning methods can generalize despite these limitations. To address the potential for ReLERNN to serve as an asset for researchers working with low-quality data—for example, those studying nonmodel organisms—we simulated 1-Mb chromosomes under a randomized fine-scale recombination landscape, and then masked increasing fractions of both genotypes and sites. We then trained ReLERNN with both missing genotypes and genome inaccessibility, and generated predictions on the simulated chromosomes.

We show that ReLERNN exhibits high accuracy and low bias on data sets with missing genotypes, even as the fraction of missing data increases to half of all genotypes (fig. 5). Moreover, we found that ReLERNN had reduced bias and significantly lower absolute error than LDhelmet at 50% missing genotypes for both n = 4 and n = 20 ($T\le -2.8$; P_WTT < 0.007 for both comparisons). Here, we define missing genotypes as any genotype call set to a “.” in the VCF, although in theory, a simple quality threshold to identify missing genotypes could also be implemented. Additionally, we tested ReLERNN across increasing levels of genome inaccessibility (up to 75% of all sites inaccessible), simulating a scenario where the vast majority of sites cannot be accurately mapped—for example, in low-complexity genomic regions or for taxa without reference assemblies. Here, genome inaccessibility refers to any site overlapping a window in the accessibility mask, where the entire genotype array at this site is discarded. Again, ReLERNN exhibited reduced bias in error across all levels of genome accessibility relative to LDhelmet (supplementary fig. S20, Supplementary Material online). However, levels of absolute error were not significantly different between the methods after correcting for multiple tests ($T\le -2.1$; $P_{\text{WTT}}\ge 0.043$ for all comparisons). Together, these results suggest that ReLERNN may be of particular interest to researchers studying nonmodel organisms or for those without access to high-quality reference assemblies.

Fig. 5.

(A) Distribution of raw error ($r_{\text{predicted}}-r_{\text{true}}$) for LDhelmet and ReLERNN when presented with varying levels of missing genotypes for simulations with n = 4 and (B) n = 20 chromosomes. (C) Fine-scale rate predictions generated by ReLERNN for a 1-Mb recombination landscape (gray line) simulated with varying levels of missing genotypes, for n = 4 and (D) n = 20 chromosomes.

Recombination Landscapes Are Largely Concordant among Populations of African D. melanogaster

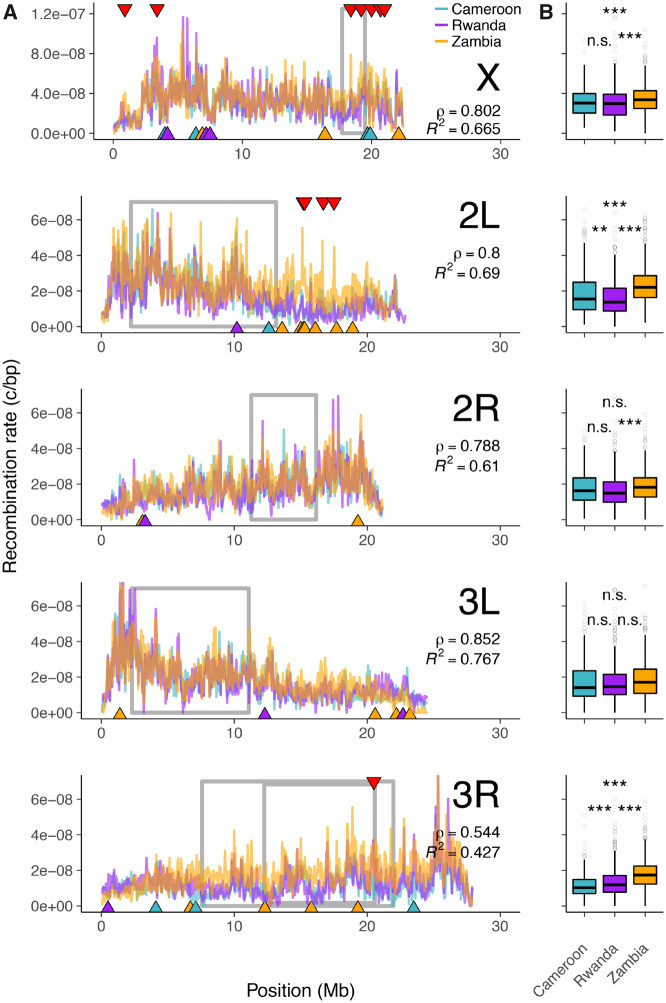
Using our method, we characterized the genome-wide recombination landscapes of three populations of African D. melanogaster (sampled from Cameroon, Rwanda, and Zambia). Each population was derived from the sequencing of ten haploid embryos (detailed in Pool et al. 2012; Lack et al. 2015), hence these data represent an excellent opportunity to exploit ReLERNN’s high accuracy on small sample sizes. The lengths of genomic windows selected by ReLERNN were roughly consistent among populations, and ranged from 38 kb for chromosomes 2R, 3L, and 3R in Zambia, to 51 kb for the X chromosome in Cameroon. We show that fine-scale recombination landscapes are highly correlated among all three populations of D. melanogaster (genome-wide mean pairwise Spearman’s $\rho =0.76$; $P<{10}^{-16}$; 100-kb windows; fig. 6). The genome-wide mean pairwise coefficient of determination between populations was somewhat lower, $R^2=0.63$ ($P<{10}^{-16}$; 100-kb windows), suggesting there may be important population-specific differences in the fine-scale drivers of allelic association. These differences may also contribute to within-chromosome differences in recombination rate between populations. Indeed, we estimate that mean recombination rates are significantly different among populations for all chromosomes with the exception of chromosome 3L ($P\le 3.78\times {10}^{-4}$; one-way analysis of variance). Post hoc pairwise comparisons suggest that this difference is largely driven by an elevated rate of recombination in Zambia, identified on all chromosomes ($P\le 8.21\times {10}^{-4}$; Tukey’s HSD tests) except for 3L ($P_{\text{HSD}}\ge 0.15$). ReLERNN predicts the recombination rate in simulated test sets to a high degree of accuracy for all three populations ($R^2\ge 0.93$; $P<{10}^{-16}$; supplementary fig. S23, Supplementary Material online), suggesting that we have sufficient power to discern fine-scale differences in per-base recombination rates across the genome.

Fig. 6.

(A) Genome-wide recombination landscapes for Drosophila melanogaster populations from Cameroon (teal lines), Rwanda (purple lines), and Zambia (orange lines). Gray boxes denote the inversion boundaries predicted to be segregating in these samples (Corbett-Detig and Hartl 2012; Pool et al. 2012). Red triangles mark the top 1% of global outlier windows for recombination rate. Blue, purple, and orange triangles mark the top 1% of population-specific outlier windows for recombination rate, with triangle color indicating the outlier population (see Materials and Methods). (B) Per-chromosome recombination rates for each population. Spearman’s ρ and R² are reported as the mean of pairwise estimates between populations for each chromosome. **P < 0.01 and ***P < 0.001 are based on Tukey’s HSD tests for all pairwise comparisons.

When comparing our recombination rate estimates to those derived from experimental crosses of North American D. melanogaster (reported in Comeron et al. 2012), we find that the coefficients of determination averaged over all three populations were $R^2=0.46,0.70,0.47,0.08,0.73$ for chromosomes 2L, 2R, 3L, 3R, and X, respectively (supplementary fig. S24, Supplementary Material online; 1-Mb windows). These results differ from those observed by Chan et al. (2012), who compared 22 D. melanogaster sampled from the same Rwandan population with the FlyBase map and found $R^2=0.55,0.63,0.45,0.42,0.41$ for the same chromosomes. The minor differences we observed between methods for chromosomes 2L, 2R, 3L, and the X chromosome can likely be attributed to the fact that we are comparing estimates from two different methods, using different African flies, to a different experimentally derived map. However, the larger differences found between methods for chromosome 3R seem less likely attributable to methodological differences. Importantly, African D. melanogaster is known to harbor large polymorphic inversions often at appreciable frequencies (Lemeunier and Aulard 1992; Aulard et al. 2002). For example, the inversion In(3R)K segregates in our Cameroon population at p = 0.9. These differences in inversion frequencies potentially contribute to the exceptionally weak correlation observed using our method for chromosome 3R.

An important cause of population-specific differences in recombination landscapes might be population-specific differences in the frequencies of chromosomal inversions, as recombination is expected to be strongly suppressed between standard and inversion arrangements. To test for an effect of inversion frequency inferences made by ReLERNN, we resampled haploid genomes from Zambia to create artificial population samples with the cosmopolitan inversion In(2L)t segregating at varying frequencies, $p\in \{0.0,0.2,0.6,1.0\}$. In Zambia, In(2L)t arose recently (Corbett-Detig and Hartl 2012) and segregates at p = 0.22 (Lack et al. 2015), suggesting that recombination within the inversion breakpoints may be strongly suppressed in individuals with the inverted arrangement relative to those with the standard arrangement. For these reasons, we predict that the inferred recombination rate should decrease as the low-frequency inverted arrangement is increasingly overrepresented in the set of sampled chromosomes (i.e., as more of the samples contain the high-LD inverted arrangements). As predicted, we found a strong effect of the sample frequency of In(2L)t on estimated rates of recombination for chromosome 2L in Zambia (supplementary fig. S27, Supplementary Material online), demonstrating that ReLERNN is sensitive to the frequency of recent inversions.

To further explore population-specific differences in recombination landscapes, we took a statistical outlier approach, whereby we define two types of recombination rate outliers—global outliers and population-specific outliers (see Materials and Methods). Global outliers are characterized by windows with exceptionally high variance in rates of recombination between all three populations (fig. 6; red triangles), whereas population-specific outliers are those windows where the rate of recombination in one population is strongly differentiated from the rates in the other two populations (fig. 6; population-colored triangles). We find that population-specific outliers, but not global outliers, are significantly enriched within inversions (P = 0.005; randomization test; fig. 6; gray boxes). Moreover, this enrichment remains significant when extending the inversion boundaries by up to 250 kb ($P_{\text{rand}}\le 0.004$). However, extending the inversion boundaries beyond 250 kb, or restricting the overlap to windows surrounding only the breakpoints (250 kb, 500 kb, 1 Mb, 2 Mb), erodes this pattern ($P_{\text{rand}}\ge 0.055$ for all comparisons), suggesting that the role for inversions in generating population-specific differences in recombination rates is complex, at least for these populations.

Selection is another important factor that may confound the inference of recombination rates. For instance selective sweeps generate localized patterns of high LD on either side of the sweep site (Kim and Nielsen 2004; Schrider et al. 2015); thus, regions flanking selective sweeps may mimic regions of reduced recombination. Inasmuch population-specific selective sweeps are expected to contribute to population-specific differences in recombination rate estimates. We used diploS/HIC (Kern and Schrider 2018) to identify hard and soft selective sweeps in our African D. melanogaster populations, and we tested for an excess of recombination rate outliers overlapping with windows classified as sweeps. In total, diploS/HIC classified 27.4%, 28.1%, and 26.8%, of all genomic widows as selective sweeps (either “hard” or “soft”) for Cameroon, Rwanda, and Zambia, respectively, when looking at 5-kb nonoverlapping windows. The associated false discovery rates (FDR) for calling sweeps in these populations were appreciable: 33.9%, 33.1%, and 34.7%, respectively (supplementary fig. S26, Supplementary Material online). As expected, windows classified as sweeps had significantly lower rates of recombination relative to neutral windows in all three populations ($P_{\text{WTT}}\le {10}^{-16}$ for all comparisons; supplementary fig. S25, Supplementary Material online). However, we found that neither global- nor population-specific outliers were enriched for selective sweeps ($P_{\text{rand}}\ge 0.246$ for both comparisons), suggesting that, when treated as a class, recombination rate outliers are not likely driven by sweeps in these populations. When treated separately (i.e., independent permutation tests for each recombination rate outlier window), we identified seven outliers enriched for sweeps at the $P\le 0.05$ threshold, corresponding to an expected FDR of 77%. However, given our FDR for calling sweeps in these populations, our measure of the enrichment in overlap with recombination rate outliers is likely to be conservative. Two of these outlier windows may represent potential true positives; an outlier in Cameroon contains five out of six nonoverlapping 5-kb windows classified as “hard” sweeps, the second from Rwanda has 10 out of 12 windows classified as “hard” sweeps (P_rand = 0.0 for both comparisons). These two recombination rate outlier windows are potentially ripe for future studies on selective sweeps in these populations, and suggest that in at least some instances, selection contributes to observed differences in estimates of recombination rates between Drosophila populations.

Discussion

We introduced a new method, ReLERNN, for predicting the genome-wide map of per-base recombination rates from polymorphism data, through the use of deep neural networks. Importantly, ReLERNN is particularly well suited to take advantage of emerging small-scale sequencing experiments—for example, those traditionally associated with the study of nonmodel organisms. Population genomics, as a field, relies on estimates of recombination rates to understand the effects of diverse phenomena ranging from the impacts of natural selection (Elyashiv et al. 2016), to patterns of admixture and introgression (Price et al. 2009; Brandvain et al. 2014; Schumer et al. 2018), to polygenic associations in genome-wide association studies (Bulik-Sullivan et al. 2015). As befits this need, there has been a long tradition of development of statistical methods for estimating the population recombination parameter, $\rho =4Nr$ (Hudson and Kaplan 1985; Hudson 1987, 2002; Wakeley 1997; Wall 2000; McVean et al. 2002; Wiuf 2002; Li and Stephens 2003; Myers and Griffiths 2003; Chan et al. 2012; Lin et al. 2013; Gao et al. 2016).

We sought to harness the power of deep learning, specifically deep recurrent neural networks, to address the problem of estimating recombination rates, and in so doing, we developed a workflow that reconstructs the genome-wide recombination landscape to a high degree of accuracy from very small sample sizes—for example, four haploid chromosomes or directly from allele frequencies obtained through Pool-seq. The use of deep learning has recently revolutionized the fields of computer vision (Krizhevsky et al. 2012; Szegedy et al. 2015), speech recognition (Hinton et al. 2012), and natural language processing (Sutskever et al. 2014), and although its use in population genomics has only recently begun, it is anticipated to be similarly fruitful (Schrider and Kern 2018). The natural extension of deep learning to population genomic analyses comes as a result of the ways in which ANNs learn abstract representations of their inputs. In the case of population genomic analyses, the inputs can be naturally represented as DNA sequence alignments, eliminating the need for human oversight (and potentially constraint) in the form of statistical summaries (i.e., compression) of the raw data. ANNs can then learn high-dimensional statistical associations directly from the sequence alignments, and use these to return highly accurate predictions.

ReLERNN utilizes a variant of an ANN, known as a GRU, as its primary technology. GRU networks excel at identifying temporal associations (Jozefowicz et al. 2015), and therefore, we modeled our sequence alignment as a bidirectional time series, where each ordered SNP represented a new time step along the chromosome. We also modeled the distance between SNPs using a separate input tensor, and these two inputs were concatenated after passing through the initial layers of the network (see fig. 1 inlay). We demonstrated that ReLERNN can predict a simulated recombination landscape with a high degree of accuracy ($R^2=0.93$; fig. 2), and that the accuracy of these predictions remain high, even when using small sample sizes ($R^2=0.82$; supplementary fig. S4, Supplementary Material online). These predictions compared favorably with those made by leading composite likelihood methods (LDhat and LDhelmet; McVean et al. 2002; Chan et al. 2012), as well as other machine learning methods (the CNN and FastEPRR; fig. 3).

We also showed that ReLERNN can achieve modest accuracy when presented solely with allele frequencies derived from simulated Pool-seq data, especially when sequenced at the relatively modest depth of 5× the pool size (supplementary fig. S7, Supplementary Material online). Moreover, ReLERNN performed well at estimating recombination rates in the face of missing genotype calls—exhibiting reduced bias when compared with LDhelmet, even with 50% of genotypes missing (fig. 5) or 75% of the genome inaccessible to SNP calls (supplementary fig. S20, Supplementary Material online). Together, these results suggest that ReLERNN will be well suited to the increasing amount of population genomic data from nonmodel organisms. Although the abstract nature of the data represented in its internal layers constrains our ability to interpret the exact information ReLERNN relies on to inform its predictions, our experiments using incorrect assumed mutation rates (supplementary figs. S8 and S9, Supplementary Material online) suggest that ReLERNN is potentially learning the relative ratio of recombination rates to mutation rates. Because the assumed rate of mutation governs the inherent potential for ReLERNN to resolve recombination events—that is, recombination events cannot be detected without informative SNPs—and because simulation results suggest ReLERNN is more accurate when overestimating $\overline{\mu }$ relative to underestimating it, we suggest erring on the side of overestimating $\overline{\mu }$. For these reasons, however, an extra caveat is warranted—use caution when interpreting the results from ReLERNN as absolute measures of the per-base recombination rate unless precise mutation rate estimates are also known. This actually presents an opportunity—we suspect that ReLERNN (or a related network) has the potential to infer the joint landscape of recombination and mutation, though this task likely poses an additional set of unknown challenges.

Demographic model misspecification is another potential source of error that should affect not only deep learning methods targeted at estimating ρ but also likelihood-based methods. Historical demographic events (e.g., population bottlenecks and rapid expansions), because they may alter the structure of LD genome-wide, can bias inference of recombination based on genetic variation data. Our simulations demonstrated that although all the methods we tested had elevated error in the context of demographic model misspecification, ReLERNN remained the most accurate across all misspecification scenarios (fig. 4). Although we caution against generalizing too much from this experiment, the model misspecification tested here was extreme: we are replacing a human-like demography of a bottleneck followed by exponential growth with a model of constant population size. We suspect that ReLERNN, by using an RNN, is able to encode higher order allelic associations across the genome, for instance three-locus or four-locus LD, and in so doing capture more of the information available than traditional methods that use composite likelihoods of two-locus LD summaries. Additionally, there are clear opportunities for future improvements to ReLERNN. For instance, our simulation studies demonstrated that the GRU used by ReLERNN is also sensitive to gene conversion events (supplementary fig. S19, Supplementary Material online), thus, the joint estimation of rates of recombination and gene conversion may be quite feasible. Ultimately, it remains far from clear what network architectures will be best suited for population genetic inference, though we remain optimistic that ANNs will prove useful for a variety of applications in the field.

A natural application of ReLERNN, due in part to its high accuracy with small sample sizes, was to characterize and compare the recombination landscapes for multiple populations of African D. melanogaster, for which few populations with large samples sizes are currently available. Previous estimates of genome-wide fine-scale recombination maps in flies have focused on characterizing recombination in experimental crosses (Comeron et al. 2012), or by running LDhat (or the related LDhelmet) on populations with relatively moderate sample sizes (i.e., $\ge 22$ samples) (Chan et al. 2012; Langley et al. 2012). Here, we applied ReLERNN to three populations for which at least ten haploid embryos were sequenced: Cameroon, Rwanda, and Zambia (Pool et al. 2012; Lack et al. 2015). Generally, recombination landscapes were well correlated among populations. Mean pairwise coefficients of determination among all three populations were $R^2=0.69,0.61,0.77,0.43,0.66$ for chromosomes 2L, 2R, 3L, 3R, and X, respectively. These correlations are notably lower than those observed in humans (Myers et al. 2005) and mice (Wang et al. 2017), and one potential biological cause for this large difference could be the cosmopolitan chromosomal inversions that segregate in African D. melanogaster (Corbett-Detig and Hartl 2012; Lack et al. 2015).

Our results suggest that recombination suppression extends well beyond the predicted breakpoints of the inversion (at least 5 Mb beyond in the case of In(2L)t; supplementary figs. S27 and S28, Supplementary Material online). This large-scale suppression of recombination due to inversions in Drosophila has been observed both directly in experimental crosses (Dobzhansky and Epling 1948; Novitski and Braver 1954; Kulathinal et al. 2009; Miller et al. 2016; Fuller et al. 2018), and indirectly from patterns of variation surrounding known inversion breakpoints (Corbett-Detig and Hartl 2012; Langley et al. 2012). Although it is true that the negative relationship between inversion frequency and recombination should only exist for inversions segregating at low frequencies (e.g., crossover suppression is not expected in inversion homozygotes), we predict a negative relationship to dominate in these populations, as the majority of polymorphic inversions are young, segregate at low frequencies, and show elevated LD along their lengths perhaps due to the actions of natural selection (Corbett-Detig and Hartl 2012; Lack et al. 2015).

Although polymorphic inversions exert strong effects on recombination landscapes, support for their role in explaining the most diverged regions among populations was mixed—we found that population-specific recombination rate outliers, but not global outliers, were significantly enriched within the inversions known to segregate in these populations (fig. 6). Moreover, our predictions for the relative rates of recombination among populations, based on inversion frequencies per chromosome, were largely not met—the inversions In(2L)t, In(2R)NS, and In(3L)Ok segregate at the highest frequencies in Zambia, yet this population also has the highest average recombination rate for these three chromosomes. One might speculate that such a result could be due to the reapportioning of crossovers that occurs due to the interchromosomal effect (Schultz and Redfield 1951), although we have no firm evidence for this. Chromosome 3R, however, did match these predictions, having inversions segregating at the highest frequencies of any chromosome (e.g., $p_{In(3R)K}=0.9$ in Cameroon) and also both the lowest coefficient of determination ($R^2=0.43$) and the population-specific recombination rates ranked in accordance with inversion frequencies (fig. 6).

Given the small impact that demographic model misspecification had on our predictions, we expect at least some robustness to patterns of linked selection (e.g., background selection and hitchhiking) that can lead to skews in the site frequency spectrum, mimicking population size change. Although we did not directly test for an effect of background selection on the accuracy of ReLERNN, we did characterize patterns of recombination near selective sweep regions in Drosophila. Interestingly, although we identified two individual outlier regions characterized by numerous selective sweeps, we did not observe a significant enrichment of sweeps overlapping either global- or population-specific outliers when these outliers were treated as a class of genomic elements. This is perhaps surprising, given that selective sweeps are known to create characteristic elevations of LD (Kim and Nielsen 2004), and perhaps could mimic regions with very divergent levels of recombination in a population-specific way.

A number of other evolutionary forces might explain the existence of our outlier regions as well. For example, mutation rate heterogeneity along the chromosomes could, in principle, generate spurious peaks or troughs in our estimates of recombination rate, as ReLERNN in effect scales its per-base recombination rate estimates by a mutation rate that is assumed to be constant along the chromosome (supplementary figs. S8 and S9, Supplementary Material online). Moreover, introgression from diverged populations might affect patterns of allelic association in a local way along the genome (Schrider et al. 2018; Schumer et al. 2018). Taken together, our results suggest that although both inversions and selection can influence population-specific differences in the landscape of recombination, the preponderance of these differences likely has complex causes.

Although ReLERNN currently stands as a functional end-to-end pipeline for measuring recombination rates, the modular design herein presents a number of important opportunities for extension, with the potential to address myriad questions in population genomics. For example, the RNN structure we exploit here could be used for inferring the joint distribution of gene conversion and crossover events, or for inferring the distribution of selection coefficients and/or migration rates from natural populations. In addition, ReLERNN presents an excellent opportunity for the implementation of transfer learning, whereby ReLERNN could be trained in-house on an otherwise prohibitively extensive parameter space, allowing end-users to make accurate predictions by generating only a small fraction of the current number of simulations and training epochs presently required. The application of machine learning, and deep learning in particular, to questions in population genomics is ripe with opportunity. The software tools that we provide with ReLERNN support a simple foundation on which the population genetics community might begin this exploration.

Materials and Methods

The ReLERNN Workflow

The ReLERNN workflow proceeds by the use of four python modules—ReLERNN_SIMULATE, ReLERNN_TRAIN, ReLERNN_PREDICT, and ReLERNN_BSCORRECT (or alternatively ReLERNN_SIMULATE_POOL, ReLERNN_TRAIN_POOL, and ReLERNN_PREDICT_POOL when analyzing Pool-seq data). The first three modules are mandatory, and include functions for estimating parameters such as θ_W and N_e from the inputs, functions for masking genotypes and inaccessible regions of the genome, functions for simulating the training, validation, and test set, functions for training the neural network, and functions for predicting rates of recombination along the chromosomes. The fourth module, ReLERNN_BSCORRECT, can be used with both individually sequenced data and Pool-seq data. This module is optional (though recommended) and includes functions for estimating 95% CI and implementing a correction function to reduce bias. The output from ReLERNN is a list of genomic windows and their corresponding recombination rate predictions (reported as per-base crossover events), along with 95% CI and corrected predictions through the use of ReLERNN_BSCORRECT.

Estimation of Simulation Parameters and Coalescent Simulations

ReLERNN takes as input a VCF file of phased or unphased biallelic variants. A minimum of four sample chromosomes must be included, and users should ensure proper quality control of the input file beforehand—for example, filtering low-coverage, low-quality, and nonbiallelic sites. ReLERNN for Pool-seq takes a single file of genomic coordinates and their corresponding pooled allele frequency estimates (example files can be found at https://github.com/kern-lab/ReLERNN/tree/master/examples). ReLERNN then steps along the chromosome in nonoverlapping windows of length l, where l is the maximum window size for which the number of segregating sites, S, in all windows is $\le 1,750$. By default, we require that $S\le 1,750$, as extensive experimentation during development showed that $S\gg 1,750$ has the potential to cause the so-called exploding gradient problem to arise during training (see Pascanu et al. 2013). However, the maximum S allowed per window is a user-configurable parameter ($--\mathit{maxSites}$), and can be increased at the expense of potential training failures. The minimum number of sites in a window is another user-configurable parameter ($--\mathit{minSites}$ in ReLERNN_PREDICT) and is set to 50 by default. As a result of independently estimating l for each chromosome, the output predictions file may return different window sizes for different chromosomes, depending on SNP densities.

Once l has been estimated, ReLERNN_SIMULATE uses the coalescent simulation software, msprime (Kelleher et al. 2016), to independently generate 10⁵ training examples and 10³ validation and test examples. By default, these simulations are generated under assumptions of demographic equilibrium using the following parameters in msprime: [$\mathit{sample}\_\mathit{size}=n$, where n is the number of chromosomes in the VCF; $Ne=N_{\mathrm{e}}$, where $N_{\mathrm{e}}=\frac{{\theta }_{\mathrm{w}}}{4\overline{\mu }{l}_{\text{max}}}$ and $\overline{\mu }$ is the assumed genome-wide per-base mutation rate, l_max is the maximum value for l across all chromosomes, and ${\theta }_{\mathrm{w}}=\frac{S_{\text{max}}}{a_{\mathrm{n}}}$ where S_max is the genome-wide maximum number of segregating sites for all windows and $a_{\mathrm{n}}={\sum }_{i=1}^{n-1}\frac{1}{i}$; $\mathit{mutation}\_\mathit{rate}=U({\mu }_{\text{low}},{\mu }_{\text{high}})$, where ${\mu }_{\text{low}}=\frac{2\overline{\mu }}{3}$ and ${\mu }_{\text{high}}=\overline{\mu }+\frac{\overline{\mu }}{3}$; $\mathit{recombination}\_\mathit{rate}=U(0.0,r_{\text{max}})$, where $r_{\text{max}}=\frac{{\rho }_{\text{max}}}{\overline{\mu }}$, and $\text{length}=l_{\text{max}}$]. In addition to simulating under equilibrium, ReLERNN can also simulate under a population size history inferred by one of three programs: stairwayplot (Liu and Fu 2015), SMC++ (Terhorst et al. 2017), or MSMC (Schiffels and Durbin 2014). This is handled by proving the raw final output file to ReLERNN_SIMULATE using the $--\mathit{demographicHistory}$ option. When a demographic history is supplied to ReLERNN, the Ne parameter in msprime is substituted with a history of population size changes through time, but the $\mathit{mutation}\_\mathit{rate},\hspace{0.17em}\mathit{recombination}\_\mathit{rate}$, and length parameters are the same as when simulating under constant population size. After each simulation is completed, ReLERNN writes both the genotype matrix and a vector of SNP coordinates to temporary.npy files, which are later used during batch generation.

Sequence Batch Generation and Network Architectures

To reduce the large memory utilization common to the analysis of genomic sequence data, we took a batch generation approach using the fit_generator function in Keras—that is, only small batches (defaulty $\mathit{batch}\_\mathit{size}=64$) of simulation examples are called into memory at any one time. Moreover, both the order of examples within each batch and the order of individuals within a single training example are randomly shuffled (i.e., sample 1 is not always at the top of the genotype matrix). Data normalization and padding occur when a training batch is called, and the genotype and position arrays are read into memory. The zeroth axis of the genotype and positions arrays is then padded with 0 s ($\mathit{pad}\_\mathit{size}=5$) to $\text{max}(S_{\text{max}},S_{\text{sim}})$, where S_max is the genome-wide maximum number of segregating sites for all windows in the samples and S_sim is the maximum number of segregating sites generated across all training, validation, and test simulations. Padding was added only to the right-hand side of the genotype and positions matrices for the analyses presented here. However, padding on both sides (i.e., centering the data) is an available option.

The targets for each training batch are the per-base recombination rates used by msprime to simulate each example. These targets are z-score normalized across all training examples. Genotypes and positions are not normalized, per se. Rather, the genotype matrix encodes alleles as reference (−1), alternative (1), or padded/missing data (0), and variant positions are encoded along the real number line ($0-1$). In the case of ReLERNN for Pool-seq, we convert the simulated genotypes into allele frequencies by sampling with replacement the vector of alternative and reference alleles for all sites to the assumed mean read depth of the pool (a user supplied parameter). We then exclude any site where the sampled variant is fixed or where p < 0.05, and stack this newly created allele frequency vector with the vector of positions. Here, allele frequencies (but not positions) are z-score normalized. The normalized and padded genotype, position, and allele frequency arrays form the input tensors to our neural networks, and take the shapes defined in supplementary figure S1, Supplementary Material online.

ReLERNN trains a recurrent neural network with Keras (Chollet et al. 2015) using a Tensorflow backend (Abadi et al. 2015). The complete details of our neural architecture can be found in the python module https://github.com/kern-lab/ReLERNN/blob/master/ReLERNN/networks.py, and a detailed flow diagram showing the connectivity between layers as well as network parameters can be found in supplementary figure S1, Supplementary Material online. Briefly, the ReLERNN neural network utilizes distinct input layers for the genotype and position tensors, which are later merged using a concatenation layer in Keras. The genotype tensor is first fed to a GRU layer, as implemented with the bidirectional wrapper in Keras, and the output of this layer is passed to a dense layer followed by a dropout layer. On the positions side of the network, the input positions tensor is fed directly to a dense layer and then to a dropout layer. Dropout (Srivastava et al. 2014) was used extensively in our network, and accuracy was significantly improved when employing dropout relative to networks without dropout. Once concatenated, output from the dropout layer is passed to a final round of dense and dropout layers, and the final dense layer returns a single z-score normalized prediction for each example, which is unnormalized back to units of crossovers per-base. ReLERNN implements early stopping to terminate training ($\mathit{min}\_\mathit{delta}=0.01$, patience = 100) and uses the “Adam” optimizer (Kingma and Ba 2014) and a mean squared error (MSE) loss function. Our hypertuning trials were completed via a grid search over the set of parameters: recurrent layer output dimensions (64, 82, 128), loss function (MSE, MAE), input merge strategy (concatenate, average), and dense layer output dimensions (64, 128), optimizing for MSE.

Total runtime estimates are highly dependent on: 1) the number of epochs needed to train before the early stopping threshold is met (which can vary extensively) and 2) the coalescent simulation parameters (most notably recombination rate and population size). As an example, the total runtime for ReLERNN_SIMULATE, ReLERNN_TRAIN, and ReLERNN_PREDICT on a 1-Mb chromosome with 90,290 segregating sites [parameters: n = 20, $\overline{r}=7.6\times {10}^{-9}$, and $\overline{\mu }=2.5\times {10}^{-8}$], which trained for 348 epochs before terminating, was 8,527 s (40 cores Intel Xeon, 1 NVIDIA 2070 GPU). Total runtimes are not strongly influenced by genome size—for example, the time needed for ReLERNN to make predictions on the 90,290 SNPs in the example above was <8.2 s.

Parametric Bootstrap Analysis and Prediction Corrections

ReLERNN includes the option to generate CIs around each predicted recombination rate and correct for potential biases generated during training. To accomplish this, we used parametric bootstrapping, as implemented by ReLERNN_BSCORRECT in the following way: after the network has been trained and predictions have been generated, ReLERNN_BSCORRECT simulates 10³ test examples for each of 100 recombination rate bins drawn from the distribution of recombination rates used to train the network. The parameters for each new simulation example are drawn from the same distribution of parameters used to simulate the original training set, with the exception of $\mathit{recombination}\_\mathit{rate}$, which is held constant for each rate bin. Predictions are then generated for these 10⁵ simulated test examples using the previously trained network, generating a distribution of predictions for each respective recombination rate bin. About 95% CI is calculated for each bin by taking the upper and lower 2.5% predictions from this distribution of rates.

The distribution of test predictions can potentially be biased in systematic ways—for example, predictably underestimating rates of recombination for those examples with the highest simulated crossover events, possibly due to the limited ability to resolve high recombination rates with a finite number of SNPs. From our inferred CIs, we can correct for inferred bias in the following way. The bias correction function takes each empirical prediction, r_predicted, and identifies the nearest median value, $\tilde{Y}$, from the distribution of 10⁵ bootstrap rate predictions (supplementary fig. S3, Supplementary Material online). Because each $\tilde{Y}$ was generated from a rate bin corresponding to the true recombination rate, Y, we can apply the correction function, $f(r_{\text{prediction}})=r_{\text{prediction}}+(\tilde{Y}-Y)$, to all predictions. This method has the effect of increasing r_predicted in areas of parameter space where we are reasonably confident that we are underestimating rates and reducing r_predicted in areas where we are likely to be overestimating rates. ReLERNN_BSCORRECT is provided as an optional module for this task, as the resimulation of 10⁵ test examples has the potential to be computationally expensive, and may not be warranted in all circumstances. However, as stated above, the extent of the computational expense is highly dependent on the parameters used in the coalescent simulation, and may not always contribute substantially to total runtimes. For example, ReLERNN_BSCORRECT increased the total runtime in the example mentioned above by 8.6% (9,266 s compared with 8,527 s).

Testing the Accuracy of ReLERNN on Simulated Recombination Landscapes

To test the accuracy of ReLERNN at recapitulating a dynamic recombination landscape, we ran our complete ReLERNN workflow on simulation data replicating chromosome 2L of D. melanogaster. Using crossover rates estimated by Comeron et al. (2012), we simulated varying numbers of samples of D. melanogaster chromosome 2L with msprime using the RecombinationMap class [parameters: $n\in \{4,20,50\},\hspace{0.17em}\overline{\mu }=2.8\times {10}^{-9},\hspace{0.17em}{N}_{\mathrm{e}}=2.5\times {10}^5$]. Simulated samples were exported to a VCF file using ploidy = 1, and all simulations were generated under demographic equilibrium. We used these simulated VCF files as the input to our ReLERNN pipeline, where we varied the assumed $\overline{\mu }$ and the assumed ratio of ρ_max to θ given to ReLERNN. The assumed $\overline{\mu }$ was varied from 50% less than the rate used in simulations ($2.8\times {10}^{-9}$) to 50% greater than the true rate. Likewise, the ratio of ρ_max to θ was either held constant, resulting in the training set containing on an average higher or lower per-base recombination rates than the true rate, or was adjusted to correctly reflect the true maximum per-base recombination rate used—that is, approximately $1.2\times {10}^{-7}$ crossovers per base. To run ReLERNN on simulated Pool-seq data, we used the same VCFs generated above, but converted all variants to allele frequencies in the following way: for all sites in the VCF, we resampled the variant haplotypes with replacement to a simulated read depth of $d\in \{\frac{n}{2},1n,2n,5n\}$ and then excluded all sites where the resampled variant was fixed or where p < 0.05.

Comparative Methods

We chose to compare ReLERNN with three published methods for estimating recombination rates—FastEPRR (Gao et al. 2016), a 1D CNN recently described in Flagel et al. (2019) and both LDhat (McVean et al. 2002) and LDhelmet (Chan et al. 2012). We generated a training set (used by ReLERNN and the CNN) with 10⁵ examples and tested all of the methods on an identical set of $5\times {10}^3$ simulation examples. We generated two classes of simulations, one simulated under demographic equilibrium and the other using a demographic history derived from European humans (CEU model; Gravel et al. 2011; Tennessen et al. 2012). Both classes of simulations were generated for $n\in \{4,8,16,32,64\}$, where n is the number of chromosomes sampled from the population. All simulations were generated in msprime with the common set of parameters [$\mathit{recombination}\_-\mathit{rate}=U(0.0,6.25{\mathrm{e}}^{-8}),\hspace{0.17em}\mathit{mutation}\_-\mathit{rate}=U(1.875{\mathrm{e}}^{-8},3.125{\mathrm{e}}^{-8}),\hspace{0.17em}\mathit{length}=3{\mathrm{e}}^5$].

For both ReLERNN and the CNN, the same training set consisting of 10⁵ examples was used to train each neural network, and the same test examples were used to compare the predictions produced by each method. Comparisons with LDhat and LDhelmet were made using the above training examples to parameterize the generation of independent coalescent likelihood lookup tables. For each set of examples of sample size n, we used the known value of ρ_max from the simulated training examples, and we then calculated the average per-base values for θ from the simulated test examples using Watterson’s estimator. These parameter values were passed to the functions for lookup table generation in LDhat and LDhelmet [LDhat options: –n, –rhomax, –theta, and $-n\_\mathit{pts}$ 101; LDhelmet options: –r 0.0 0.1 10.0 1.0 100.0]. For LDhelmet, we also ran the pade function using the options [–x 12 and $--\mathit{defect}\_\mathit{threshold}$ 40]. The resulting tables were used to make predictions on our $5\times {10}^3$ test examples using the pairwise function for LDhat and $\mathit{max}\_lk$ function for LDhelmet [options: $--\mathit{max}\_lk\_\mathit{start}$ 0.0 and $--\mathit{max}\_lk\_\mathit{resolution}$ 0.000001]. Comparisons with FastEPRR were made by transforming the genotype matrices resulting from our test simulations into fasta-formated input files, and running the FastEPRR_ALN function [using format = 1] in R. As LDhat, LDhelmet, and FastEPRR all predict ρ, the resulting predictions were transformed to per-base recombination rates for direct comparison with ReLERNN using the function $r=\frac{{\rho }_{\text{pred}}\times {\mu }_{\text{true}}}{{\theta }_{\mathrm{W}}}$, where ρ_pred is the prediction output by each method, and θ_W and μ_true are Watterson’s estimator and the true per-base mutation rate used in the simulation example, respectively. To compare accuracy among methods, we directly compared the distribution of absolute errors ($|r_{\text{predicted}}-r_{\text{true}}|$) for each method for each set of examples of sample size n.

To test the effects of model misspecification on predictions, we simply directed ReLERNN and the CNN to use a training set generated under demographic equilibrium for making predictions on a test set generated under the CEU model, and vice versa. To test for the effects of model misspecification in LDhat and LDhelmet, we generated a lookup table using parameter values estimated from the misspecified training set (e.g., the lookup table used for predicting the CEU model test set was generated by using parameter values directly inferred from training simulations under equilibrium). We did not directly test the effect of model misspecification using FastEPRR, as this method takes as input only a fasta sequence file, and therefore, the internal training of the model was not able to be separated from the input sequences. To address the effects of model misspecification, we also directly compared the distribution of absolute errors ($|r_{\text{predicted}}-r_{\text{true}}|$). Additionally, we compared the marginal error directly attributable to model misspecification among methods. We defined marginal error as ${ϵ}_{\mathrm{m}}-{ϵ}_{\mathrm{c}}$, where ϵ_m and ϵ_c are equal to $|r_{\text{predicted}}-r_{\text{true}}|$ when the model is misspecified and correctly specified, respectively. We simulated gene conversion test sets using ms (Hudson 2002), with a mean conversion tract length of 352 bp (corresponding to the mean empirically derived tract length in D. melanogaster; Hilliker et al. 1994) and simulated a range of gene conversion to crossover ratios, $\frac{r_{\text{GC}}}{r_{\text{CO}}}\in \{0,1,2,4,8\}$.

Training on Missing Genotypes and Inaccessible Regions of the Genome

Deep neural networks, through their aptitude for pattern recognition, can be trained to infer information from missing data. To harness this ability, we took two different approaches: 1) we infer patterns of recombination when some fraction of individual genotype calls are absent (missing genotypes) and 2) we infer these patterns when some fraction of all sites cannot be sequenced (genome inaccessibility). To simulate levels of missing genotypes similar to those found in real data, we first sample the distribution of all missing genotypes from the input VCF. We then generate a missing genotype mask for all windows in the genome and write this mask as a temporary file to the disk. Simulation proceeds as if all genotypes are present, however during batch generation, one random mask is drawn from the genomic distribution of masks and applied to the generated genotype matrix, setting some fraction of genotype calls to 0 (the same element used to pad). This has the effect of training the network to infer recombination, even where genotype calls are missing in real data. To infer recombination in the face of genome inaccessibility, we take a similar approach. Here, ReLERNN accepts an empirical accessibility mask similar to that provided by the 1000 Genomes project (1000 Genomes Project Consortium et al. 2015). This is provided in BED format, which is then fragmented into smaller arrays corresponding to the window size used by ReLERNN_SIMULATE. After simulation proceeds with all sites present, we randomly draw a mask from the distribution of empirical accessibility masks, and apply it during batch generation, removing all sites marked inaccessible from the array. We then remove the corresponding sites from the positions array, and train as usual.

To test ReLERNN’s ability to learn recombination rates in the face of missing genotypes and genome inaccessibility, we simulated a 1-Mb randomize dynamic recombination landscape in msprime. Here, we randomly selected 39 sites along the chromosome to serve as recombination rate breakpoints, generating 40 windows of different rates. For each rate multiplier, $m\in \{3,3,3,3,3,5,5,5,5,5,7,7,7,10,10,10\}$, we randomly selected a window to have the recombination rate $m\overline{r}$, where $\overline{r}=2.5\times {10}^{-9}$ is the simulated background recombination rate. To simulate missing genotypes, we randomly set genotype calls in the simulated VCF to a “.”, corresponding to a fraction of total genotypes $\in \{0.0,0.10,0.25,0.50\}$. To simulate an empirical accessibility mask, we simply sampled directly from the phase 3 1000 Genomes accessibility masks (1000 Genomes Project Consortium et al. 2015) and removed sites in the VCF corresponding to a fraction of total genomic sites $\in \{0.0,0.25,0.50,0.75\}$. To directly compare between the predictions made by ReLERNN and LDhelmet, we then broke the VCF into windows of the same length (e.g., 22 kb for n = 4 and 10 kb for n = 20 for the simulations with missing genotypes). We then ran both ReLERNN and LDhelmet as described above, and compared the distribution of absolute errors ($|r_{\text{predicted}}-r_{\text{true}}|$) for each method for each set of examples of sample size $n\in \{4,20\}$.

Recombination Rate Variation in D. melanogaster

We obtained D. melanogaster population sequence data from the Drosphila Genome Nexus (https://www.johnpool.net/genomes.html, last accessed May 5, 2019; Pool et al. 2012; Lack et al. 2015). We converted Drosphila Genome Nexus “consensus sequence files” to a simulated VCF format, excluding all nonbiallelic sites and those containing missing data. We chose to analyze populations from Cameroon, Rwanda, and Zambia, as these populations contained at least ten haploid embryo sequences per population and each population included multiple-segregating chromosomal inversions (supplementary table S1, Supplementary Material online). To ensure roughly equivalent power to compare rates among populations, we downsampled both Rwanda and Zambia to ten chromosomes. We selected individual haploid genomes for each population by requiring that our sampled inversion frequencies for each of the six segregating inversions—In(1)Be, In(2L)t, In(2R)NS, In(3L)Ok, In(3R)K, and In(3R)P—closely approximate their population frequencies as measured in the complete set of haploid genomes for that population. All sample accessions and their corresponding inversion frequencies are located in the Supplementary Material online.

Before running ReLERNN, we first set out to model the demographic history for each population using each of three methods: stairwayplot (Liu and Fu 2015), SMC++ (Terhorst et al. 2017), and MSMC (Schiffels and Durbin 2014). With the exception of MSMC, all methods were run using default parameters. For MSMC, the use of default parameters generated predictions that were unusable (supplementary fig. S22, Supplementary Material online). For these reasons, and after direct communication with MSMC’s authors, we determined that running MSMC with a sample size of two chromosomes would be the most appropriate. Using all three methods, we show that inferred historical population sizes are unreliable for these populations—no two methods recapitulate the same history, and the histories generated by MSMC vary dramatically depending on the number of samples used (supplementary figs. S21 and S22, Supplementary Material online). For these reasons, and because results from our simulations suggest that marginal error due to demographic misspecification is quite low for our method (supplementary fig. S18, Supplementary Material online), we decided to simulate our training data under the assumptions of demographic equilibrium [options: $--\mathit{estimateDemography}$False $--\mathit{assumedMu}$$3.27\mathrm{e}-9$$--\mathit{upperRhoThetaRatio}$ 35].

We measured the correlation in recombination rates between each African D. melanogaster populations by recalculating the raw rate for 100-kb sliding windows, as ReLERNN will predict the rates of recombination in slightly different window sizes, depending on θ for each chromosome. The recombination rate for each 100-kb window was calculated by taking the average of all raw rate windows predicted by ReLERNN, weighted by the fraction that each window overlapped the larger 100-kb sliding window. Recombination rate outliers were identified in two ways: global outliers and population-specific outliers. Global outliers were identified by first calculating the mean and SD in recombination rates for all three populations in each 100-kb sliding window. We then used the top 1% of outliers from the distribution of residuals, after fitting a linear model to the SD on the mean. Population-specific outliers were identified by using a modification of the population branch statistic (herein PBS*; Yi et al. 2010), whereby we replaced pairwise F_ST with the pairwise differences in recombination rates. We then used the top 1% of all PBS* scores as our population-specific outliers, with each outlier corresponding to a PBS* score for a single population.

To test the effect of inversion frequency on predicted recombination rates, we resampled ten haploid chromosomes from the available set of haploid genomes from Zambia to generate sampled populations containing In(2L)t at varying frequencies, $p\in \{0.0,0.2,0.6,1.0\}$. We then ran ReLERNN on chromosome 2L for each of these resampled Zambian populations. We classified recombination windows by their overlap with the coordinates of In(2L)t (as defined in Corbett-Detig and Hartl 2012), defining windows within the breakpoints (inside), windows up to 3 Mb outside the breakpoints (flanking), and windows >3 Mb outside the breakpoints (outside). Recombination rates were negatively correlated with inversion frequency in our sample, not only within the inversion but also in regions 3 Mb outside the inversion (flanking regions) (${\rho }_{\text{Spearman}\text{'}\mathrm{s}}=-1$; P = 0.04 for both comparisons). We also saw a similar negative correlation outside the flanking regions, although this association was weakened relative to that within or flanking the inversion (supplementary fig. S27, Supplementary Material online). Importantly, varying the size of the flanking regions (from 1 to 5 Mb) produced patterns that were qualitatively identical, suggesting that the effect of inversions on recombination suppression extends far beyond the inversion breakpoints themselves (supplementary fig. S28, Supplementary Material online).

We also expect that rates of recombination should be correlated with distance to the inversion breakpoint on smaller spatial scales. Likewise, recombination rates in the inversion interior (>2 Mb from the breakpoints) are expected to be higher than in those regions immediately surrounding the breakpoints. To test this, we looked at the recombination rates in our African D. melanogaster populations, binned by distance to the nearest inversion breakpoints segregating in these populations. We classified windows by their overlap with inversion interiors (>2 Mb inside the inversion breakpoints) and their overlap with windows within 200 kb, 500 kb, 1 Mb, and 2 Mb of inversion breakpoints. We found that recombination rates in the flanking regions are positively correlated with distance to inversion breakpoints in both Rwanda and Zambia (${\rho }_{\text{Spearman}\text{'}\mathrm{s}}=1$; P = 0.04 for both comparisons) but not in Cameroon (${\rho }_{\text{Spearman}\text{'}\mathrm{s}}=0.8$; P = 0.17; supplementary fig. S25, Supplementary Material online). However, with the exception of Cameroon (inversion interior compared with <250 kb from breakpoint; P_WTT = 0.035), we did not observe this pattern ($P_{\text{WTT}}\ge 0.057$; supplementary fig. S25, Supplementary Material online).

We tested for an enrichment of both global and population-specific outliers within inversions by randomization tests, permuting the labels for outliers 10⁴ times and counting the overlap with inversions for each permutation to calculate the empirical P values. We also tested for an effect of selection on recombination rates in these populations, by running diploS/HIC (Kern and Schrider 2018) to detect selective sweeps. We ran diploS/HIC on each population, training on simulations generated under demographic equilibrium. For each population, we simulated 2,000 training examples from each of the five classes of regions required by diploS/HIC using the coalescent simulation software discoal (Kern and Schrider 2016). For simulations which included sweeps, we drew the selection coefficient from a uniform distribution such that $s\sim U(0.0001,0.005)$, the time of completion of the sweep from $\tau \sim U(0,0.05)$, and the frequency at which a soft sweep first comes under selection as $f\sim U(0,0.1)$. We drew θ from U(65, 654) and we drew ρ from an exponential distribution with mean 1,799 and the upper bound truncated at triple the mean. For the discoal simulations, we simulated 605 kb of data with the goal of classification of the central most 55-kb window. We looked at the overlap with “sweep” windows (those classified as either “hard” or “soft”) and those windows classified as “neutral” by diploS/HIC. Our complete diploS/HIC pipeline for these samples is available at https://github.com/kern-lab/ReLERNN/tree/master/manuscript. All statistical tests were completed in R (R Core Team 2018), with the exception of empirical randomization tests, which were completed using Python.

ReLERNN is currently available at https://github.com/kern-lab/ReLERNN.