Harnessing the potential of artificial neural networks for predicting protein glycosylation

Abstract

Kinetic models offer incomparable insight on cellular mechanisms controlling protein glycosylation. However, their ability to reproduce site-specific glycoform distributions depends on accurate estimation of a large number of protein-specific kinetic parameters and prior knowledge of enzyme and transport protein levels in the Golgi membrane. Herein we propose an artificial neural network (ANN) for protein glycosylation and apply this to four recombinant glycoproteins produced in Chinese hamster ovary (CHO) cells, two monoclonal antibodies and two fusion proteins. We demonstrate that the ANN model accurately predicts site-specific glycoform distributions of up to eighteen glycan species with an average absolute error of 1.1%, correctly reproducing the effect of metabolic perturbations as part of a hybrid, kinetic/ANN, glycosylation model (HyGlycoM), as well as the impact of manganese supplementation and glycosyltransferase knock out experiments as a stand-alone machine learning algorithm. These results showcase the potential of machine learning and hybrid approaches for rapidly developing performance-driven models of protein glycosylation.

Highlights

• •Artificial neural network for protein glycosylation applied to four glycoproteins.
• •Describes glycosylation dependence on nucleotides and nucleotide sugars.
• •Predicts effect of cell culture conditions on glycosylation as part of hybrid model.
• •Predicts effects of glycosyltransferase knock out experiments.
• •Accurately predicts site-specific glycoform distributions of up to eighteen glycans.

1. Introduction

N-linked glycosylation is a post-translational modification of paramount importance for protein function, folding and activity (Lee et al., 2015; Shental-Bechor and Levy, 2008; Solá and Griebenow, 2009; Li et al., 2016) and a critical quality attribute of glycoprotein therapeutics. Glycosylation includes the attachment and further modification of an oligosaccharide molecule in an Asn (N-linked glycosylation) or Ser/Thr (O-linked glycosylation) residue of the protein. Specific structural variations such as the lack of core fucose or increased levels of terminal galactose in the N-linked oligosaccharide have been found to notably increase either the complement-dependent cytotoxicity (CDC) or the antibody-dependent cellular cytotoxicity (ADCC) activity of monoclonal antibody drugs (Shields et al., 2002; Shinkawa et al., 2003; Thomann et al., 2016; Houde et al., 2010). Moreover, the glycosylation profile of cell membrane proteins has been found to differ between healthy and diseased human cells and has been identified as a qualitative diagnosis attribute of specific diseases (Varki, 2016; Reily et al., 2019; Ohtsubo and Marth, 2006). For example, patients with rheumatoid arthritis have been found to produce immunoglobulin G and A (IgG & IgA, respectively) with low levels of galactose in the crystallizable fragment (Fc) and high content of core fucosylated and bisected glycans in the antigen-binding fragment (Fab) (Ercan et al., 2010; Youings et al., 1996). N-glycoproteomics of the ovarian cell serum has been recently proposed as a robust biomarker to indicate the stage of the high-grade serous ovarian carcinoma (HGSC) in women (Sinha et al., 2019), while the upregulation of sialyltransferases and high levels of α2,6 sialic acid in N-glycoproteins of the cell surface have been positively correlated to tumour cells (Schultz et al., 2012, 2013).

The glycosylation process initiates in the Endoplasmic Reticulum with the addition of the precursor oligosaccharide in the targeted polypeptide backbone site (Aebi, 2013) and further processing occurs in the Golgi apparatus, where the oligosaccharide chain is trimmed and decorated with additional sugar residues (Stanley, 2011; Dalziel et al., 2014). N-linked glycosylation is completed with the addition of either terminal galactose or sialic acid residues. The glycosylation enzymes, embedded in the intra-Golgi membrane, mainly consist of glucosidases and glycosyltransferases with diverse functions (Stanley, 2011; Spiro, 2002). Apart from enzyme availability, glycans conformation is greatly dependent on the levels of nucleotide sugar donors (NSDs) in the Golgi. NSDs are metabolic products consisting of a nucleotide mono-/di-phosphate and a sugar molecule and act as co-substrates for the glycosyltransferases (Gerardy-Schahn et al., 2001; Hadley et al., 2014). NSD availability in the Golgi is regulated by nucleotide sugar transporters (NSTs) that reside in the Golgi membrane and are responsible for NSD translocation from the cytoplasm to the Golgi environment through a widely studied antiport mechanism (Parker and Newstead, 2019; Ishida and Kawakita, 2004; Blondeel and Aucoin, 2018).

Normally, there are two levels of glycosylation regulation in the cell: a) the glycosylation machinery and b) the glycoprotein structure. The glycosylation machinery includes all the enzymes and proteins associated with glycosylation as mentioned above. However, the extent of N-linked glycosylation is strongly dependent on the glycoprotein structure. Steric hindrance can restrict enzyme access to the oligosaccharide chain and therefore significantly affect the glycoprofile. For example, monoclonal antibodies (mAbs) present a relatively simple glycosylation profile with no tri- and tetra-antennary glycans and minor levels of sialylation due to steric hindrance in the Fc region. In contrast, erythropoietin (EPO) - a much smaller in size protein - has numerous exposed glycosites with versatile and complex glycan structures, most of which are heavily sialylated (Zhang et al., 2016).

The multi-level nature of glycosylation control makes it difficult to predict the glycoprofile of recombinantly produced proteins, with site-specific predictions being particularly challenging. Several genetic or cell culturing modifications have been proposed in order to better control the glycosylation process (Gupta and Shukla, 2018; Hossler et al., 2012; del Val et al., 2010). Kinetic and genome-scale models have been used with some success to describe it (Umaña and Bailey, 1997; Krambeck and Betenbaugh, 2005; Jimenez del Val et al., 2011; Kremkow and LeeGlyco-Mapper, 2018) and additionally describe/predict the effects of multiple culture parameters on glycosylation, such as temperature variation and addition of metabolic precursors (Zhang et al., 2020; Sou et al., 2017; Kotidis et al., 2019) or genetic engineering (McDonald et al., 2014) over the last two decades. Recently, a kinetic glycosylation model was extended to include protein folding, ER degradation and aggregation and thus describing the entire secretion pathway of the glycoprotein (Arigoni-Affolter et al., 2019). Moreover, low-parameter approaches involving probabilistic modelling frameworks representing the glycosylation network and predicting the effects of gene engineering have been recently developed (Spahn et al., 2016; Liang et al., 2020). Model development has been supported by advances in analytical methods for identifying and quantifying the glycoform distribution, like the use of NMR, LC-MS, MALDI-TOF-MS, MS/MS, HPLC and capillary electrophoresis (Zhang et al., 2016; Everest-Dass et al., 2018; Gaunitz et al., 2017).

However, all the aforementioned modelling frameworks demand a significant level of background knowledge of both the computational tools and the glycosylation process. In addition, they require considerable time for parameterization and training, particularly the mechanistic kinetic models (Medlock and Papin, 2020). Several assumptions usually accompany the selection of nominal values for model parameters, such as: a) enzyme concentration in the Golgi membrane, b) distribution of the enzymes along the Golgi and c) inhibition constants for the reaction rates. Nominal values for parameterization are usually adapted from in vitro studies of the respective enzymes in comparable organisms, which could be misleading as in vivo enzymatic behaviour and conditions might differ substantially from in vitro experiments (García-Contreras et al., 2012). Hence, as the results of the parameter estimation are strongly dependent on the initial values, they are usually not the global solution of the optimization problem but just one of potentially many sets of values that could describe the system. Additionally, the construction of the reaction network requires detailed knowledge of the reaction rules and constraints and could have a notable effect on the predictive performance of the model, especially in genetic modification experiments.

In contrast, the use of machine learning methods for the description of glycosylation requires minimum knowledge of the biological background, no construction of reaction networks and can be parameterized within a few hours. Data-driven models, like Artificial Neural Networks (ANNs), have been widely used for the description of several biological processes with the biotic phase treated as a black box (Lancashire et al., 2009; Darsey et al., 2015; Shahid et al., 2019). ANNs require minimal manual parameter estimation and can be readily adapted to each desired application. However, it should be noted that neural network parameters such as weights and biases, cannot be adequately controlled by the user. Initial parameter values are usually seeded from the library in use and the user has limited choice over their values. Nonetheless, this limitation can be tackled with the manipulation of the learning rate or the optimizer of the network. ANNs have been used to predict the location of glycosites based on the amino acid sequence of proteins (Julenius et al., 2004; Senger and Karim, 2005, 2008) and to describe cell culture processes of both mammalian (Narayanan et al., 2019; Senger and Karim, 2003) and algal cells (Del Rio-Chanona et al., 2019; Zhang et al., 2019). However, there has been no effort to utilize the ANNs in order to predict the glycoform distribution of proteins despite presenting clear advantages in terms of low parameter estimation burden.

We propose the use of ANNs to describe N-linked glycosylation of recombinant glycoproteins. We first show that ANNs can reliably describe the antibody glycosylation process subject to perturbations in metabolism using intracellular NSD concentrations as inputs. The ANN model also correctly captures the effect of manganese supplementation, the metal ion co-factor of β-1,4-galactosyltransferase, on IgG glycosylation. When the ANN is incorporated in an overarching cell culture modelling framework, the resulting hybrid, kinetic/ANN, glycosylation model (HyGlycoM) shows a notably higher degree of agreement with experimental data with a significantly reduced development and parameterization effort compared to the fully kinetic platform. Crucially, the hybrid model uses only information from the extracellular environment as input, i.e. it is better suited for online applications such as process control. Moving to more complex glycoproteins, we demonstrate that the ANN can accurately reproduce the outcome of glycoengineering on the glycoform distribution of two fusion proteins with 4 and 5 glycosites using glycosyltransferase concentrations as inputs. Having been trained on datasets for triple knockouts, the ANN model can further successfully predict the outcome of a quadruple knockout experiment. Thus, the stand-alone ANN and the hybrid ANN/kinetic models can make use of a versatile list of inputs such as the intracellular NSD concentrations, extracellular metabolite concentrations and glycosyltransferase expression levels to closely predict protein glycosylation.

2. Results

The ANN approach was applied to four different recombinantly produced proteins. The dataset for the IgG-producing cells supplemented with galactose and uridine was generated in-house as described in the Material & Methods section and in Kotidis et al. (2019). The datasets for manganese chloride, galactose and fucose addition were obtained from Villiger et al. (2016a). The datasets for the two fusion proteins, Fc-DAO and EPO-Fc, were obtained from Bydlinski et al. (2018). The inputs of the ANN model were either the experimental or calculated intracellular concentrations of nucleotides and NSDs or the extracellular metabolites concentrations in the case of the IgG products or the gene expression levels of specific glycosylation enzymes for the two fusion proteins. The output for all neural networks was the glycoform distribution profile of the produced recombinant protein. The examined fusion proteins, Fc-DAO and EPO-Fc have 5 and 4 glycosites, respectively, and therefore the output of the ANN in the knockout experiments was the site-specific glycosylation profile.

2.1. Construction of a hybrid model that describes cell metabolism and N-linked glycosylation

2.1.1. Establishing an ANN model to describe IgG N-linked glycosylation

NSD levels are known to strongly affect the glycosylation profile of the recombinant protein (Naik et al., 2018; Wong et al., 2010; Grainger and James, 2013; Sha and Yoon, 2019; Sou et al., 2015). For this reason, the experimentally determined intracellular concentrations of nucleotides and NSDs were used as inputs of the neural network. The neural network was trained with the nucleotide and NSD concentrations of four feeding experiments (P1, P2, P4 and P5, with P1 being the control experiment) and the respective glycoform distribution on days 7, 9, 11 and 12 of cell culture, when available. In total, 11 datasets were used for model training and validation, with each dataset including the profile of 12 different variables (132 points in total): intracellular concentration of AMP, ADP, ATP, CTP, UTP, GTP, UDPGalNAc, UDPGlcNAc, UDPGal, UDPGlc, GDPMan and GDPFuc. The fifth experiment (P3) was used for ANN model validation. The validation results were compared against the P3 experimental dataset in order to verify model capabilities by tuning the network hyperparameters.

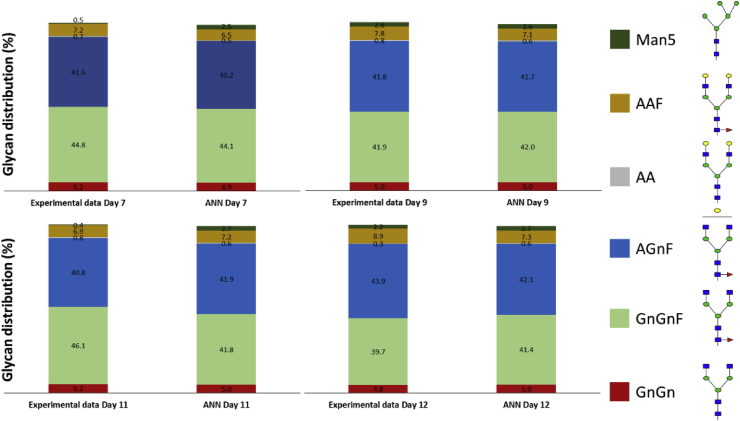
The results of the ANN glycosylation model validation for the P3 experiment are compared with the experimental data in Fig. 1. ANN model simulations closely describe the experimental data with the maximum error found on day 11 measurement of the GnGnF glycan (≅ 4.1%) due to the unexpected increase of the GnGnF relative abundance. The validation of the ANN resulted in 2 hidden layers with 22 and 18 neurons in the first and second hidden layer, respectively. The inclusion of three hidden layers was found to only marginally improve the model results and was therefore dismissed. The ANN model closely describes the glycoform distribution of the IgG for all time points with an average absolute error of 0.87%. When we trained the model with a different combination of the training and testing datasets but the same hyperparameters configuration, it remained in good agreement with experimental results (Supplementary Fig. S1).

Fig. 1.

Comparison of the ANN validation to the experimental data for four different time points during the cell culture period for the P3 experiment.

Several kinetic models have attempted to describe the complex network of nucleotides and NSD synthesis, either accounting for the entire synthesis network (Jedrzejewski et al., 2014) or reduced networks (Sou et al., 2017; Kotidis et al., 2019), while other efforts have been undertaken in order to calculate the fluxes of the NSDs towards the Golgi apparatus and the glycosylation model (Sha et al., 2019). However, the Monod-type equations used in kinetic mechanistic models to describe NSD synthesis and protein glycosylation do not account for more complex phenomena that occur during protein synthesis, such as variations in the expression levels of NSTs and glycosylation enzymes, which could significantly affect the resulting glycosylation profile (Wong et al., 2010; Grainger and James, 2013). Moreover, the assumption of a linear relationship between the intracellular concentration of NSDs (Krambeck and Betenbaugh, 2005) or the flux of the NSD towards the Golgi (Sha et al., 2019) and the intra-Golgi NSD concentration neglects the regulation exerted by NSTs (i.e. SLC35), which determine and control the flow of NSDs to the Golgi apparatus. The proposed data-driven ANN model, on the other hand, has been demonstrated to tackle these problems by applying complex non-linear relationships between the inputs (nucleotides and NSDs) and the outputs (recombinant protein glycoform distribution) subject to sufficiently informative training datasets. The use of ANNs avoids the need to mechanistically describe the complicated regulation of NSD transport and gene expression. The accurate description of the IgG glycoform distribution, in this case, confirms that the concentrations of NSDs and nucleotides were appropriate inputs for this network and can reliably capture the impact of galactose and uridine addition on glycosylation.

The robustness of the ANN model was examined by excluding each of the inputs one by one. As shown in Supplementary Fig. S2, the average absolute error remains minimal, ranging from 0.87% for the full dataset to 1.25% for the case where ADP is excluded. This indicates that the ANN captures the overall trend of the input set, without being excessively dependent on any of them. The training results of the ANN are shown in Supplementary Fig. S3. In order to further evaluate the performance of the ANN, the statistical-based multivariate method of Partial Least Square Regression (PLS) that has been previously found useful for the description of monoclonal antibody glycans (Sokolov et al., 2017) was applied to the relevant dataset. PLS requires reduced parameter tuning from the user and is considerably less computationally intensive. However, the ANN model outperformed the PLS prediction (Supplementary Fig. S4A) at all time points apart from the day 11 predictions of GnGnF and AGnF. The average absolute error of the PLS model prediction was 1.66%, almost double the error of the ANN prediction.

2.1.2. Hybrid glycosylation model (HyGlycoM) - coupling ANN glycosylation model with a kinetic metabolism cell model

The ANN model was coupled with the Chinese hamster ovary (CHO) cell metabolism, antibody synthesis and NSD synthesis modules of the framework presented in Kotidis et al. (2019), replacing the mechanistic glycosylation module, as shown in Fig. 2A. The resulting hybrid model utilizes the concentration of metabolites and certain amino acids in the cell culture environment as inputs. The CHO metabolism module calculates the specific growth rate and the specific antibody production rate, which are then fed to the NSD synthesis module. The latter, in turn, calculates the concentration of the NSDs in the intracellular environment that are subsequently used as an input for the ANN model.

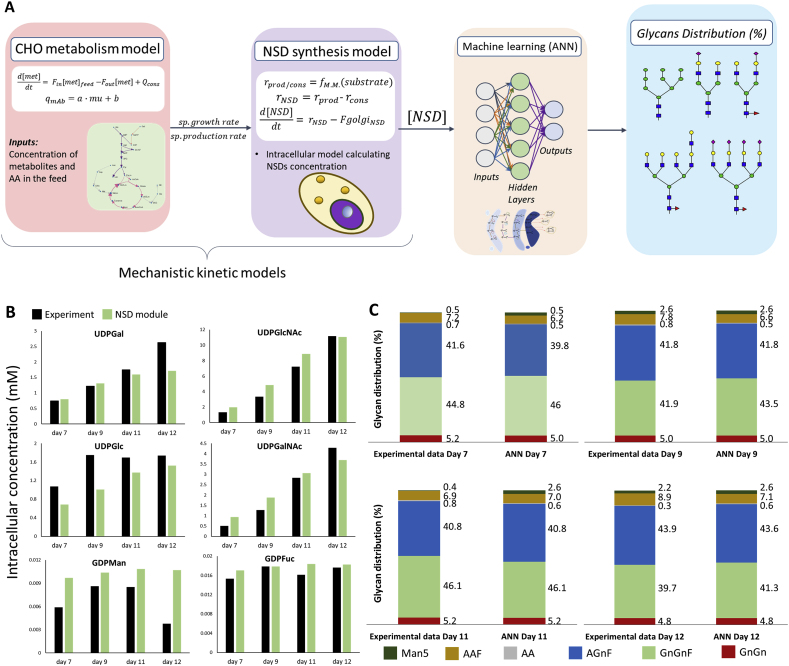
Fig. 2.

(A) Representation of the HyGlycoM, composed of a CHO metabolism kinetic model, an NSD synthesis kinetic model and an Artificial Neural Network that describes the N-linked glycosylation of the recombinant protein (IgG) in the Golgi, (B) Comparison of the kinetic module simulations for the nucleotide sugars of the P3 experiment with the experimental data. The estimated nucleotide sugars are the output of the kinetic module that is then fed as input to the ANN module, (C) Comparison of the HyGlycoM simulations for the glycans of the P3 experiment with the experimental data.

The training datasets of HyGlycoM included the P1, P2, P4 and P5 experiments. The neural network of the HyGlycoM was re-trained using the NSD concentrations calculated from the mechanistic modules of the model as inputs. Subsequently, the model was validated against the P3 experiment. The ANN module was able to absorb the inaccuracies of the kinetic modules in the estimation of the nucleotide sugars due to the correct description of the qualitative changes between the different experiments and time points from the latter, as shown in Fig. 2B. A crucial advantage of neural networks is the tolerance of inaccuracy in the input values, as long as the qualitative differences of the points are correctly described. The average absolute error between the experimental data of the P3 experiment and the HyGlycoM simulation (Fig. 2C) is 0.98%.

2.1.3. HyGlycoM outperforms the fully kinetic model

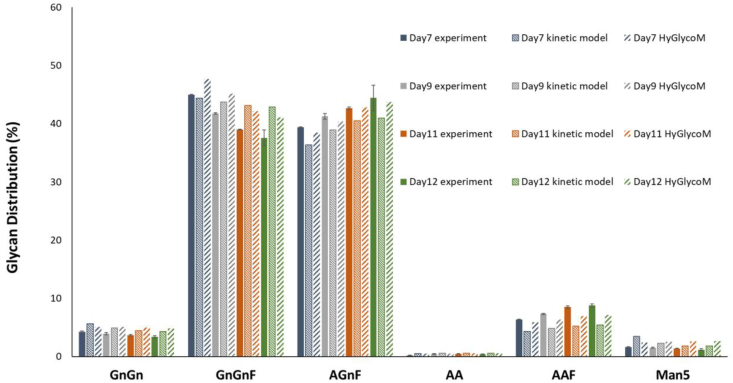
In order to further investigate the predictive capabilities of the HyGlycoM and compare the performance of the hybrid model with the respective holistic kinetic model described in Kotidis et al. (2019), both the hybrid and the kinetic model were evaluated by comparison against a sixth (P6), independent experiment also described in Kotidis et al. (2019). Results of the comparison of model predictions with the experimental data are presented in Fig. 3. The glycoprofile of the produced IgG consists mainly of the non-galactosylated GnGnF and the mono-galactosylated AGnF glycans. Within the experiments used for ANN model training, test and validation, the abundance of the GnGnF structure varies within a range from 37.6% to 53.7% and for AGnF from 34% to 44.4%

Fig. 3.

Comparison of the HyGlycoM prediction for an independent experiment (P6) with the experimental data and the prediction of the kinetic glycosylation model.

The kinetic model correctly captures the profile of GnGnF on days 7 and 9 of the culture compared to the ANN prediction. However, the ANN better describes GnGnF concentration for the following two time points and for almost all the time points for the remaining glycans, reducing that way the average absolute error by 30% compared to the kinetic model. The HyGlycoM predictions presented an average of ≅ 1.25% absolute error when compared to the experimental data. More specifically, the predictions of the galactosylated glycans for the hybrid model are notably closer to the respective experimental measurements than the kinetic model. The shortcoming of the kinetic glycosylation module being insensitive to moderate changes in NSD concentrations is therefore efficiently tackled by its replacement with the ANN glycosylation model. However, this reduced sensitivity of kinetic models can be proven useful for the reliable description of cellular processes that carry a high degree of inherent variability and show different profiles from batch to batch. Unlike kinetic models, ANNs can be unpredictably sensitive to slight changes in inputs, which can lead to dramatic loss of accuracy. In order to further evaluate the HyGlycoM predictive capabilities compared to other multivariate methods, a PLS model was trained on the P1–P5 data. The HyGlycoM significantly outperformed the PLS predictions for the P6 experiment, as shown in Supplementary Fig. S4B.

2.2. Extending the ANN to predicting the effect of metal ion addition on IgG glycosylation

Metal ions are critical co-factors of glycosyltransferases and can significantly affect enzyme activity (Lairson et al., 2008). More specifically, manganese (in the form of MnCl₂) acts as a co-factor for the N-acetylglucosaminyltransferases and β-1,4-galactosyltransferases and is usually included in culture media in order to enhance protein galactosylation. Efforts to incorporate extracellular manganese concentration in mechanistic glycosylation models have been previously described (Karst et al., 2017; Villiger et al., 2016b). Herein, we propose an ANN configuration with the additional inclusion of the cumulative manganese concentration in the inputs set to describe the effects of the co-factor on IgG glycosylation.

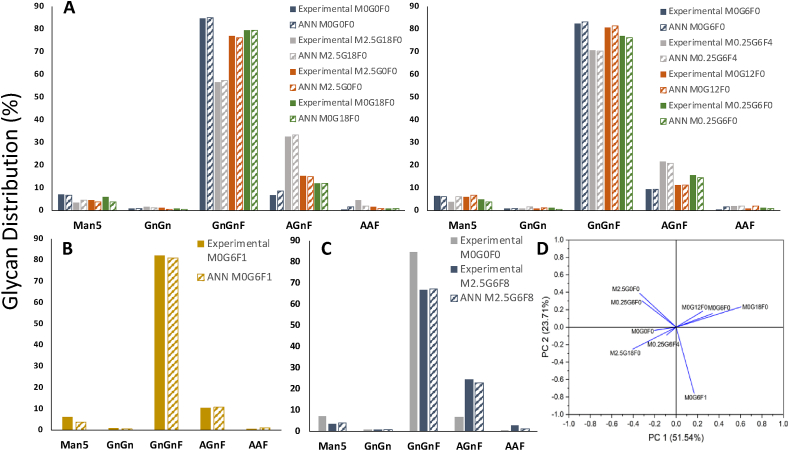
In Villiger et al. (2016a), the authors examine the effect of different levels of manganese, galactose and fucose addition to fed-batch CHO cell cultures. Briefly, an IgG-producing CHO–S cell line was cultured in 10 ​mL bioreactors with a downwards shift in pH and temperature introduced on day 5. Cells were harvested on day 17 and glycans of the Fc-region were quantified. The cumulative concentrations of manganese, galactose and fucose added in each experiment can be found in Supplementary Table S1. For the ANN training, the cumulative concentration of manganese was included in the inputs in addition to the intracellular nucleotides and NSD concentrations at day 17. The effect of galactose and fucose addition was reflected in the NSD levels and therefore the metabolites were not included in the inputs. The ANN was trained in eight experiments and validated against a ninth experiment (M0G6F1). For the selection of the validation experiment, a principal component analysis (PCA) was performed on the available dataset. The M0G6F1 was chosen for validation as it was found not to cluster with any other experiments (Fig. 4D). The ANN predictive capability was then tested against an independent experiment outside the training space (M2.5G6F8).

Fig. 4.

ANN model fitting to: (A) the experimental data used for model training, (B) the experiment used for model validation and (C) the experimental data reserved for testing the model’s predictive capabilities. In graph C the control experiment (M0G0F0) was included as well in order to show the effect of manganese, galactose and fucose addition to antibody glycosylation. (D) PCA performed on the available datasets in order to identify correlations between experiments. Abbreviation: M: manganese; G: galactose; F: fucose.

As presented in Fig. 4A and B the ANN was accurately trained with the training and validation sets in order to adequately describe the effect of manganese, galactose and fucose addition on IgG glycoprofile. Only when 2.5 ​μM manganese is added in combination with galactose does the shift from the non-galactosylated GnGnF to the mono-galactosylated AGnF glycan become prominent. The predictive capabilities of the ANN model were then evaluated against an independent experiment and the results are shown in Fig. 4C. The ANN accurately describes the glycan distribution and the changes in AAF and AGnF levels between the control (M0G0F) and the feeding experiment (M2.5G6F8).

2.3. Application of an ANN model to predict the outcome of gene knockouts

When the experimental objective is a radical change of the glycoform distribution of the recombinant protein, host cell lines are genetically engineered in order to favour specific pathways of glycosylation (Yang et al., 2015; Wang et al., 2018; Yin et al., 2015). In Bydlinski et al. (2018), the authors examine the contribution of four different β-1,4 galactosyltransferases (b4GalT1, b4GalT2, b4GalT3, b4GalT4) to the site-specific glycosylation of an EPO-Fc and an Fc-DAO protein, by creating stable cell lines with triple and ultimately quadruple knockouts, while the recombinant proteins are transiently expressed.

The expression levels of the four enzymes reported for each cell line in Bydlinski et al. (2018) were used as the input for the ANN, while the site-specific glycoform distribution of either the EPO-Fc or Fc-DAO was considered as the output. In order to examine both the fitting and predictive capabilities of the configured ANN model, two studies were performed: a) in the fitting study, the three triple knockout experiments were used as the training set and the quadruple knockout experiments as the validation set, b) in the predictive study, two of the three knockout experiments were used as the training set, the third triple knockout experiment as the validation set and finally the ANN model was used to predict the glycoform distribution of the quadruple knockout experiment de novo (test set). A 3% error with normal distribution around the measured values was introduced in the inputs and outputs in order to generate 16 artificial points for each experiment and therefore increase the robustness of the ANN model training step and reduce the risk of overfitting (Zhang et al., 2019; Tulsyan et al., 2018).

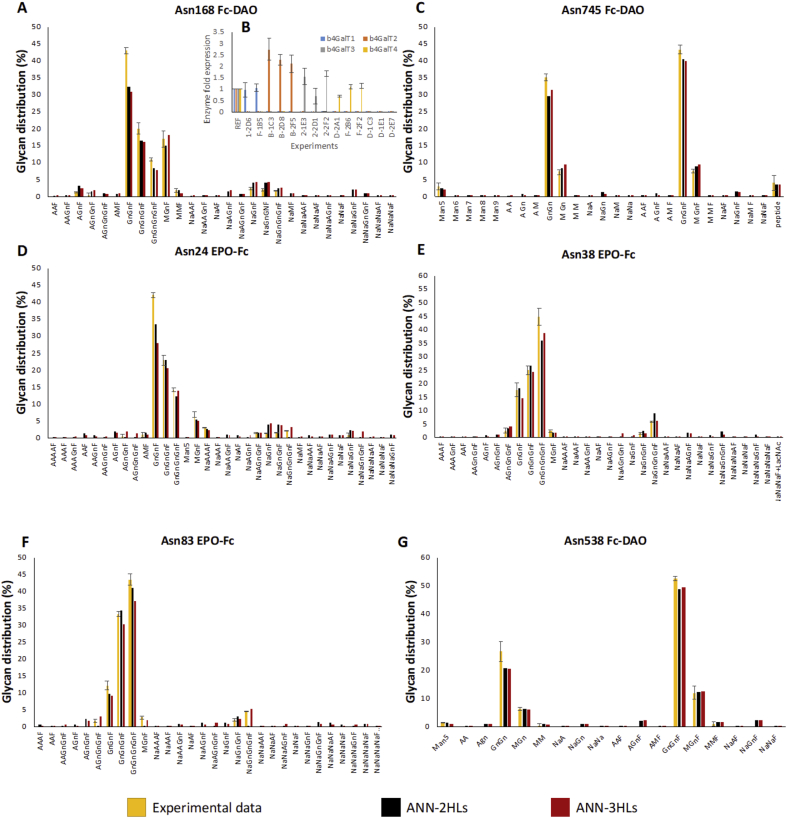
In order to account for the variability in enzymatic expression in the different clones with the same gene knockouts (Fig. 5B), the glycoform distribution of each clone was individually included in the training and validation datasets. The fitting of the ANN model to the experimental data is presented in Fig. 5A,5C-G. A configuration of three hidden layers examined Asn38 EPO-Fc and Asn538 Fc-DAO residues (Fig. 5E, G), resulted in a slightly improved fitting compared to the two hidden layers ANN model. On the other hand, the inclusion of a third hidden layer for the rest of the examined asparagine residues did not improve model fitting (Fig. 5A, C, D, F). Thus, considering the excessive computational time required for training and validation of the three hidden layers model and the minor improvements achieved, the rest of the experiments were only represented with a two hidden layer ANN. With the exception of the Asn538 glycosite of Fc-DAO (Fig. 5G) that presented a variety of 18 different glycans, the rest of the residues in Fig. 5 showed an even more complex glycoform distribution with 26–34 glycans measured across the different clones. Despite this, the model closely tracked the glycoform distribution of the knockout cell lines for most of the glycosites and for both proteins, with the exception of the Asn24 EPO-Fc that presented the highest number of different glycan species (34). As shown in Fig. 5, the ANN model is, in some cases, unable to capture the complete disappearance of glycans that were present in the wild type and triple gene knockouts. However, the fitting of the model for the most abundant glycans accurately matched the experimental data. The discrepancies for the GnGnF distribution in Fig. 5A and D are due to the overestimation of the low abundant glycans that correspond to more complex structures.

Figure 5.

(A), (C–G): ANN glycosylation model fitting for three different glycosites in the Fc-DAO and EPO-Fc proteins. The performance of networks with two and three hidden layers was examined. (B): Expression of each b4GalT isoform in each engineered cell line with respect to the expression of the enzyme in the wild type (REF). The experimental data for A, C-G graphs are the average of the quadruple knockout b4GalT1/2/3/4 ​cell lines (D-1C3, D-1E1 and D-2E7). The experimental data for all graphs (A–G) are taken from Bydlinski et al. (2018). The glycans included in the graphs were present in the glycoform distributions of at least three of the triple knockout clones but were not detected in the quadruple knockout cell lines. Glycans measured in low abundances (<1%) in one or two knockout cell lines were not included in the analysis.

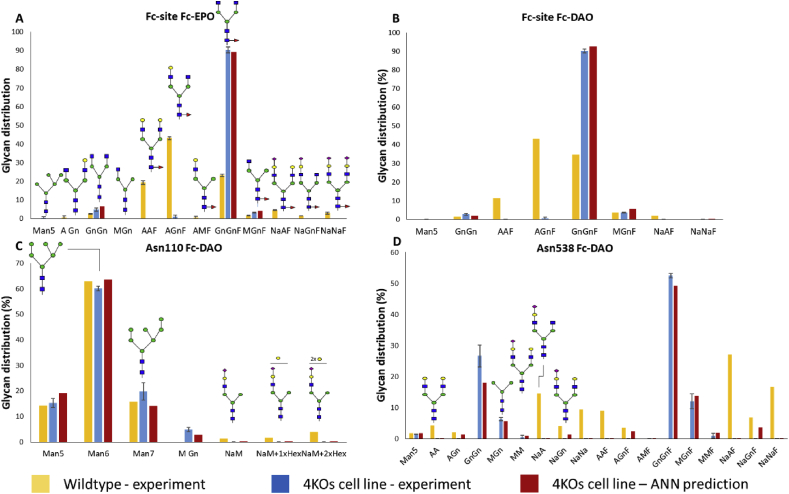
The ANN model was subsequently used for predicting the glycans present in glycosites on both EPO-Fc and Fc-DAO (Fig. 6). The neural network presented an average absolute error of 1.1% compared to the experimental data of the quadruple knockouts. The Asn110 residue of Fc-DAO (Fig. 6C) showed minor changes between the wildtype and the quadruple knockout cell lines as the wildtype concentration of galactosylated glycans in this specific site was negligible. However, the mutation of all four galactosyltransferases resulted in an immense alteration of the glycoform distribution in the Fc-site of both EPO-Fc and Fc-DAO proteins and the Asn538 site of Fc-DAO. The ANN model was correctly trained on the contribution of each galactosyltransferase from the triple knockout data and was therefore successful in predicting the glycoform distribution of the quadruple knockout experiment. Although technically an extrapolation, the prediction of the quadruple knockout glycoform distribution was based on the assumption that the ANN was provided with enough data to accurately weigh the contribution of each individual β-1,4-galactosyltransferase towards the synthesis of each individual glycan.

Fig. 6.

ANN glycosylation model predictions for the Fc-site of EPO-Fc (A), Fc-site of Fc DAO (B), Asn110 residue of Fc-DAO (C) and Asn538 of Fc-DAO (D) for the quadruple knockout cell lines. The experimental data of the wildtype cell line are displayed for reference.

3. Discussion

A data-driven ANN model was proposed to accurately describe the N-linked glycosylation profile of IgG monoclonal antibodies, EPO-Fc and Fc-DAO proteins expressed in CHO cells. Initially, the ANN model was trained with experimental data for the intracellular concentration of nucleotides and NSDs from five different fed-batch experiments that included the addition of galactose and uridine to increase monoclonal antibody galactosylation. The construction and fitting of the ANN resulted in a system with 2 hidden layers and 22 and 18 neurons in the first and second layer, respectively, which presented an absolute error of 0.87% against the experimental data used for model validation. The ANN model was additionally trained on a dataset including manganese, galactose and fucose supplementation in an effort to specifically evaluate the effect of manganese on the activity of β-1,4-galactosyltransferase and therefore on the IgG glycosylation. As shown in Fig. 4C, the model was able to closely predict the changes in glycans distribution in an independent experiment of manganese, galactose and fucose feeding.

An advantage of the ANN over kinetic-mechanistic models is that the parameterization (including the estimation of the hyperparameters) is automatically performed during network training and validation and usually takes only a few hours. In contrast, the parameterization of a kinetic glycosylation model requires concise understanding of the glycosylation process and advanced know-how of parameter estimation methodologies. Sophisticated methods for parameter estimation of such models have been extensively applied in order to accelerate and strengthen the parameter estimation process (Jimenez del Val et al., 2011; Kotidis et al., 2019; Jimenez del Val et al., 2016; Hossler et al., 2007). Moreover, mechanistic glycosylation models are usually developed for a specific product of interest and the expansion or alteration of the reaction network for the description of other proteins demands a detailed knowledge of the cell line (e.g. genetic modifications) and glycosylation enzymes preferences. Even in the work presented by Krambeck et al. (2009) where the reaction network is automatically generated to describe complex protein glycoform distributions, the user has to define the necessary enzymatic and reaction rules and constraints for network construction.

In an effort to utilize extracellular data for predicting IgG glycosylation with the use of neural networks, the ANN model replaced the kinetic glycosylation module in the mechanistic modelling framework presented in Kotidis et al. (2019). The resulting hybrid HyGlycoM model consisted of two kinetic modules describing CHO cell metabolism and NSD synthesis, feeding the ANN glycosylation model with the estimated levels of the NSDs in the intracellular environment. The use of the kinetic modules for the description of the extracellular and intracellular metabolic profile, instead of an additional ANN, provides HyGlycoM with the flexibility to adapt to alternative culture conditions in terms of the feeding schedule and medium/feed composition. A reliable kinetic model can additionally calculate the NSD concentrations and feed them to the glycosylation ANN, thereby reducing the number of experimental measurements required for glycoform prediction. The HyGlycoM was used to predict the glycoform distribution of an IgG monoclonal antibody in a series of feeding experiments, demonstrating the ability of the ANN model to absorb the inaccuracies of the kinetic modules that were used to estimate the model inputs (Fig. 2B). The HyGlycoM error on the predicted glycoform distribution was calculated at 1.25%, slightly higher than the standard deviation of the experimental measurements which was 0.93%. Finally, when compared with the fully mechanistic framework that includes the kinetic glycosylation module, HyGlycoM improved the average absolute error by 30%. The HyGlycoM adaption to new process conditions such alternative cell lines or mild hypothermia is limited by the necessary re-estimation of kinetic parameters and the inclusion of the appropriate metabolic pathways in the kinetic modules. In a similar manner, the ANN module could require re-training on new control datasets when the process conditions differ significantly from the initial training sets.

Finally, the ANN glycosylation model was trained in triple β-1,4-galactosyltransferase isoforms knockout experiments and used to either simulate or predict the effect of a quadruple b4GalT knockout experiment on the site-specific glycosylation profile of recombinant EPO-Fc and Fc-DAO (Figs. 5 and 6) with a 1.1% absolute average error. Significantly, and despite not usually being reliable for extrapolation, the ANN model presented herein closely predicts the protein glycoform distribution outside the training space (Fig. 2, Fig. 3, Fig. 4, Fig. 6) for networks with up to 18 different glycan species, when it is supplemented with appropriate data for training. The glycoform distribution of these fusion proteins is akin to that found on host cell proteins of CHO cells. Efforts to describe the greatly complex glycoform distribution of the host cell proteins of CHO cells using kinetic models have been recently undertaken (Krambeck et al., 2017). Krambeck et al., (2017) first constructed a vast reaction network of up to 15,000 oligosaccharides and 50,000 reactions to describe the complex glycoform distribution of the CHO cell proteome and then trained the kinetic model to the experimental data of several mutant CHO cell lines (knockouts of glycosylation enzymes and nucleotide sugar transporters) by varying the concentration of glycosylation enzymes in the Golgi. However, it was shown that acquiring satisfying fitting demanded the simultaneous estimation of all the enzyme concentrations included in the study, unlike the current work where no further assumptions on the behaviour of the rest of the enzymes were considered.

Whilst the implementation of neural networks requires minimal knowledge of the biological background of the described system, be it glycosylation or another cellular mechanism, the construction of such a network requires great caution. In order for an ANN to be predictive, apart from the large amount of data required for its adequate training, the user needs to correctly choose the inputs of the network. It is essential that these inputs have a biological connection to the requested outputs and that there are cellular mechanisms underlying these connections, in order for the ANN to accurately predict independent experiments. Moreover, different analytical methods for the quantification of NSDs (i.e. MALDI-TOF-MS or HPAEC), enzyme levels (i.e. RNA-seq, qRT-PCR, WB) and glycan distribution (i.e. LC-MS, MALDI-TOF-MS, gel or capillary electrophoresis) are available. Similarly to kinetic models, the experimental method used for inputs and outputs quantification should be consistent amongst the training, validation and test sets.

The availability of a wider range of data would enable the application of the ANN or hybrid model in more versatile conditions. More specifically, the combination of data for both glycosylation and metabolic gene expression (i.e. RNA-seq) and nucleotide sugar intracellular availability would constitute a more comprehensive input dataset. The adaptability of neural networks in combination with the current capabilities for deep analysis of cellular profile could contribute towards the development of a model that is translatable between different cell lines (i.e. CHO–K, CHO–S, CHO-DG44) and could be used for the identification of the optimal host for recombinant protein expression. Beyond recombinant protein synthesis, ANNs can prove useful in identifying metabolic markers for human disorders that involve alternations in protein glycosylation.

4. Conclusions

An alternative modelling framework of describing N-linked glycosylation of recombinant proteins that makes use of Artificial Neural Networks was proposed herein. The model, either as a stand-alone ANN or as part of a hybrid model combining both kinetic relationships describing CHO cell metabolism and the data-driven network describing glycosylation, was successful in simulating and predicting the glycoform distribution of four different recombinant proteins expressed in three different CHO cell lines (GS-CHO, CHO–K1, CHO–S), two IgG monoclonal antibodies and two fusion proteins (EPO-Fc and Fc-DAO). It used inputs at either the metabolite or enzyme levels to accurately describe the glycoform distribution of all four products, giving accurate site-specific predictions for the effect of quadruple glycosyltransferase knockouts on the glycoforms of EPO-Fc and Fc-DAO. Being less computationally demanding than kinetic models, the ANN glycosylation model could greatly assist the design of glycoengineering strategies or application of glycosylation control during cell culture.

5. Materials & methods

5.1. Cell culture

All the experimental data used for model construction, training and validation were taken from literature (Kotidis et al., 2019; Villiger et al., 2016a; Bydlinski et al., 2018). Six different fed-batch experiments were used for the training and validation of the HyGlycoM model. Briefly, IgG1-producing CHO cells (kindly donated by MedImmune, Cambridge, UK) were cultured in 500 ​mL vented Erlenmeyer flasks with a working volume of 100 ​mL using CD CHO medium (Life Technologies). 10 %v/v CD EfficientFeed^M C AGT™ (Feed C) Nutrient Supplement (Life Technologies) was added every other day starting from day 2 of the culture. Six feeding experiments (P1-6) were conducted: a negative control which was only supplemented with Feed C (P1), four experiments supplemented with galactose and uridine on days 4, and 8 of the cell culture in addition to Feed C and one experiment (P6) supplemented with galactose and uridine on days 4, 6, 8 and 10 in addition to Feed C. The amount of galactose and uridine supplemented in each time point can be found in Table 1. All cultures were maintained at 36.5 ​°C, 150 ​rpm and 5% CO₂. Full details of the cell culture process and samples analysis can be found in Kotidis et al. (2019). All cultures were conducted in biological duplicates.

Table 1.

Amount of galactose and uridine added at each feeding time point and in each experiment.

Experiment	Galactose (mmol)				Uridine (mmol)
	Day 4	Day 6	Day 8	Day 10	Day 4	Day 6	Day 8	Day 10
P1	0	0	0	0	0	0	0	0
P2	1	0	1	0	0	0	0	0
P3	1	0	1	0	0.50	0	0.50	0
P4	1	0	1	0	2	2	2	2
P5	5	0	5	0	0.50	0.50	0.50	0.50
P6	0.65	0.93	0.90	0.87	0.076	0.13	0.28	1

5.2. Mechanistic-kinetic mathematical model

The kinetic model used in this study has been previously presented in Kotidis et al. (2019) and was simulated using the gPROMS 5.1.1 modelling environment (Process System Enterprise Ltd, London, U.K., www.psenterprise.com/gproms). The model consists of three modules that describe CHO cell metabolism and antibody synthesis, NSD synthesis and IgG glycosylation. The latter has been adapted from Jimenez del Val et al. (2011) by re-estimating the distribution and inhibition constants of the Golgi enzymes for the IgG product used herein and replacing NSD transport with a constant ratio (20:1) between intra-Golgi NSD and cytosolic concentrations. The inputs of the dynamic model are the concentrations of specific metabolites and amino acids (glucose, lactate, ammonia, glutamine, glutamate, asparagine, aspartate, galactose and uridine) in the media and feed. The metabolic model calculates the extracellular concentration of the metabolites and amino acids over the cell culture period and the specific cell growth and protein production rates, which are then fed to the second module of NSD synthesis. The NSD synthesis module calculates the dynamic profile of the intracellular concentration of NSDs and the fluxes of the NSDs towards the Golgi. The calculated NSD concentrations are used as inputs for the third module that describes IgG glycosylation and results in the glycoform distribution profile of the protein of interest. This modelling framework as presented in Kotidis et al. (2019) results in ±5% error range for the distribution of IgG glycans.

5.3. Artificial Neural Networks model construction

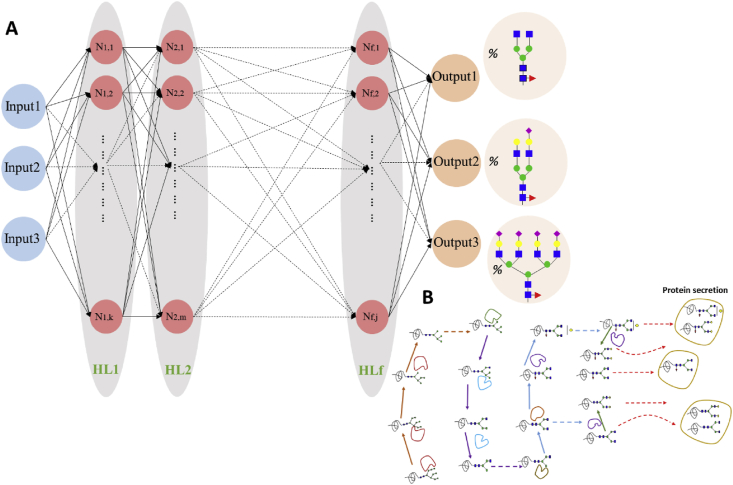
Python 3.7 was used for the construction, training and validation of the ANNs. A general representation of the ANNs used in this work is shown in Fig. 7. A typical neural network (McCulloch and Pitts, 1943) consists of one or more hidden layers, each of which includes a number of neurons or nodes . The output of the neural network is the glycan distribution of the protein of interest. The list of different glycoforms has to be pre-defined by the user. The neurons of the first hidden layer are connected to the inputs of the network through the weight of each input towards each neuron. Hence, every input has a potential impact on the value of each neuron depending on the weight of their in-between connection. In turn, the neurons of the first hidden layer (and each hidden layer thereafter) are used to estimate the value of the neurons in the subsequent hidden layer using an activation function and the respective weight, until the values of the final layer neurons (outputs) are estimated. Then, the difference between the network outputs and the provided data is calculated and through the backpropagation method the weights of each connection are re-estimated until the number of training iterations has been reached. In the work presented herein, the sigmoid activation function was chosen as it has been successfully applied in relevant works for bioprocess modelling (del Rio-Chanona et al., 2016). The number of training iterations was set to 20,000, apart from the model used for the manganese experiments that included 2000 epochs as they were found to be sufficient for error minimization. The examined ANN configurations included two or three hidden layers.

Fig. 7.

(A) Schematic diagram of an Artificial Neural Network (ANN): The depicted ANN consists of 3 inputs, 3 outputs, f hidden layers (HL) and a variable number of nodes (neurons) for each HL. The output in the studies presented herein was the glycoform distribution. The dashed lines are used to show the connections between and with the neurons that are not depicted in the graph. (B) Graphical representation of the N-linked glycosylation process in the Golgi apparatus. Arrows of different colour indicate the reactions taking place in different Golgi compartments and dashed arrows indicate protein transfer or secretion: cis (orange), medial (purple), trans (blue) and TGN (green). (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

Including more than three hidden layers bears the risk of overfitting and was found to significantly increase parameter estimation time without improving model accuracy in this particular application. Apart from keeping the network as “shallow” as possible by using the minimum number of hidden layers and neurons required to adequately describe the system, common methods used for avoiding overfitting, include the dropout, noise introduction and weight constraint methods. More specifically, in the dropout method, inputs and neurons are removed during training in a probabilistic manner, while in noise introduction the user creates artificial points by adding an error distribution to the inputs. Bias was set to zero as it was found to not contribute to the predictive capabilities of the neural networks. Additionally, the hidden layers of the ANN model should not be considered a representation of the Golgi apparatus compartments in the current study.

After training, the ANN was subjected to validation where the number of neurons and hidden layers (hyperparameters) were tuned in order to minimize error between model simulations and the experimental data for the dataset of interest (validation set), based on the strategy proposed in Del Rio-Chanona et al. (2019). For the validation simulations, the objective function was set as the minimization of the sum of the absolute difference between the experimental measurements and the simulation results for the examined dataset (Eq. (1)).

$$OF=min\sum _i\left|E{G}_i-N{G}_i^{m,h1,h2,\dots ,hm}\right|$$ (1)

where, $OF$ is the value of the objective function, $i$ are the different glycans, $E{G}_i$ is the experimentally measured value of each glycoform and $N{G}_i^{m,h1,h2,\dots hm}$ is the simulated value of the $i^{th}$ glycan for an ANN with $m$ hidden layers and with $h1,h2,\dots ,hm$ number of neurons for hidden layers $1,2,\dots ,m$ respectively.

The average absolute error for each set of model predictions was calculated using Eq. (2):

$$AAE=\frac{{\sum }_i\left|E{G}_{i,k}-N{G}_{i,k}\right|}{n}$$ (2)

where, $AAE$ is the value of the average absolute error, $E{G}_{i,k}$ is the experimentally measured value of the $i^{th}$ glycoform in the $k^{th}$ set considered for training or prediction, $N{G}_{i,k}$ is the simulated or predicted value of the ANN for the $i^{th}$ glycoform in the $k^{th}$ point and $n$ is the total number of points considered, calculated as the product of the total number of glycans and the total number of sets.

The ANN predictive capabilities were verified: a) against an independent experiment (P6 or M2.5G6F8) of interest that was not used for either training or validation for the cell culturing experiments and b) against the quadruple knockout of β-1,4-galactosyltransferase isoforms for the gene engineering experiments. All the data and models that support this study can be found in: https://github.com/PK1617/ANN-glycosylation.

5.4. Multivariate analysis methods

OriginPro 2020 (OriginLab, Northampton, MA, USA) was used for the implementation of the PCA and PLS methods.

CRediT authorship contribution statement

Pavlos Kotidis: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Visualization, Writing - original draft, Writing - review & editing. Cleo Kontoravdi: Formal analysis, Methodology, Funding acquisition, Supervision, Writing - review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: