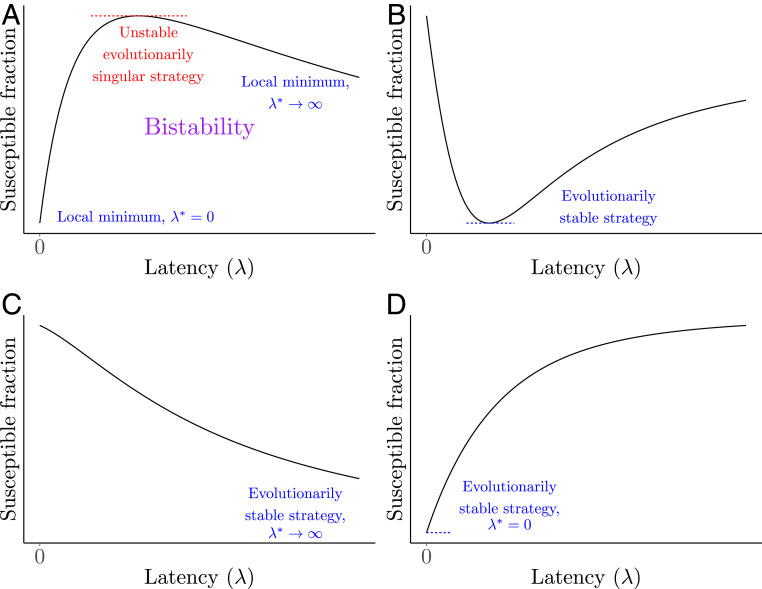
Fig. 3.

Schematics of possible evolutionary outcomes for latency $\lambda$. (A) The equilibrium susceptible fraction $\hat{S}$ has a single maximum that is an unstable evolutionarily singular strategy. In this case, there are two local stable minima of susceptible fractions at $\lambda *=0$ and $\lambda *\to \infty$. Thus, this system exhibits bistability. (B) The evolutionary outcome in this case is nonzero latency, as there exists a value that minimizes the susceptible fraction, and so it is an evolutionarily stable strategy. As nearby mutants cannot invade, this is a continuously stable strategy. (C) The susceptible fraction at equilibrium is a strictly decreasing function of $\lambda$, and so the evolutionarily stable (and also continuously stable) strategy is $\lambda *\to \infty$. (D) The susceptible fraction is a strictly increasing function of latency, and so the evolutionarily stable (and continuously stable) strategy is at zero latency ($\lambda *=0$).