Agreement threshold on Axelrod’s model of cultural dissemination

Pádraig MacCarron; Paul J Maher; Susan Fennell; Kevin Burke; James P Gleeson; Kevin Durrheim; Michael Quayle

doi:10.1371/journal.pone.0233995

. 2020 Jun 2;15(6):e0233995. doi: 10.1371/journal.pone.0233995

Agreement threshold on Axelrod’s model of cultural dissemination

Pádraig MacCarron ^1,^2,^*, Paul J Maher ¹, Susan Fennell ², Kevin Burke ², James P Gleeson ², Kevin Durrheim ³, Michael Quayle ^1,³

Editor: Carlos Gracia-Lázaro⁴

PMCID: PMC7266322 PMID: 32484846

Abstract

Shared opinions are an important feature in the formation of social groups. In this paper, we use the Axelrod model of cultural dissemination to represent opinion-based groups. In the Axelrod model, each agent has a set of features which each holds one of a set of nominally related traits. Survey data has a similar structure, where each participant answers each of a set of items with responses from a fixed list. We present an alternative method of displaying the Axelrod model by representing it as a bipartite graph, i.e., participants and their responses as separate nodes. This allows us to see which feature-trait combinations are selected in the final state. This visualisation is particularly useful when representing survey data as it illustrates the co-evolution of attitudes and opinion-based groups in Axelrod’s model of cultural diffusion. We also present a modification to the Axelrod model. A standard finding of the Axelrod model with many features is for all agents to fully agree in one cluster. We introduce an agreement threshold and allow nodes to interact only with those neighbours who are within this threshold (i.e., those with similar opinions) rather than those with any opinion. This method reliably yields a large number of clusters for small agreement thresholds and, importantly, does not limit to single cluster when the number of features grows large. This potentially provides a method for modelling opinion-based groups where as opinions are added, the number of clusters increase.

Introduction

To understand the societal structure of opinions, or attitudes, it is necessary to model the emergence of the groups that bind them. Much research demonstrates that people evaluate and understand their environment with reference to relevant social groups [1–3]. Importantly, shared opinions and beliefs are a defining feature of social groups [4, 5] and group identity can be fostered by coordinating attitudes. In particular, opinion-based groups are social structures in which people are connected by the opinions they share; and clusters of opinions become interlinked signifiers of group identity when they are jointly held by the members of a group [6].

In this paper we demonstrate that an adapted version of Axelrod’s model of cultural dissemination [7] can be used to model opinion-based groups. Axelrod modeled people as each holding one of several available traits for each of several features. The individual’s culture is defined as their combination of traits; and multiple individuals are said to share the same culture if they are spatial neighbours who share the exact combination of traits. We remove this spatial constraint when identifying clusters and instead get groups of agents sharing the same traits for each feature, we refer to these as opinion-based groups.

The social structure of opinion-based groups has similar properties to Axelrod’s model. Specifically, agents in Axelrod’s model are linked according to the values they hold (which Axelrod called “traits”) on a given number of cultural “features”. Opinion-based groups are formed by people holding a particular selection of attitudes. In principle, conceptualising Axelrod’s nominal cultural features and traits as ordinal attitudes will allow us to model the emergence of opinion-based groups with a data structure that maps cleanly on to raw survey data. Note that opinion surveys typically use ordinal Likert-type response items (e.g. an item with several response options from Strongly Disagree to Strongly Agree). While these are frequently treated as interval data in analyses (ie. assuming consistent intervals between scale points and allowing arithmetic operations such as addition and subtraction), there is a strong argument that individual Likert-type items should properly be treated as ordinal, allowing only non-arithmetic operations [8]. The original Axelrod model of cultural dissemination relies only on swapping, and our adaptions adds ranking, making it an excellent fit with Likert-type data.

The tendency toward consensus in the standard Axelrod model poses a further problem for modelling the emergence of opinion-based groups with attitudinal surveys. Specifically, it has been shown that for the final state to have many clusters, a high initial number of traits q is required [9]. Given that attitudinal surveys naturally assess more attitudes than response-options, an Axelrod simulation of such data would converge towards uniformity. However, in real social systems survey data frequently reveals stable systems of cultural diversity [10]. Our adaptation of the Axelrod model is intended to account for diversity in the structure of opinion-based groups. The idea to use surveys with the Axelrod model is not new, for example, [11] use survey data to set the initial states of the agents. In this paper, however, we approach this as a theoretical model and do not use empirical data as in, for example, [12–14].

There have been many variations on the standard Axelrod model (some even proposed in the original paper) often attempting to promote multiculturality. Some examples of variations are the introduction of noise [15], changing the topology from a lattice to a complex network [16], the effect of media represented by an external field [17], and, more recently, modelling it on a multi-layer network where only interactions can occur between nodes on specific layers [18]. Another variation treats each feature as a continuous variable which pull closer together when they agree or repel when they disagree [19]. This is similar to the Deffuant model [20] with more than one feature.

Here, we take a similar approach to the idea of bounded confidence. In this type of model, an agent only takes account of a neighbour’s opinion if it is within a certain interval of that [21]. We treat each specific feature as having a discrete value associated with it. We then only allow an interaction when the traits are within a certain distance from each other. This corresponds with research from social psychology which demonstrates that social judgements mediate attitude change [22]. For example, according to social judgment theory [21], the amount of attitude change caused by an interaction should depend on the perceived distance between the communication and the respondent’s original view. Specifically, at any given time there is a range of positions each person is open to holding, known as the “latitude of acceptance”. Importantly, this range is anchored by one’s current opinion. Similarly, decision making research demonstrates that people tend to display bias in evaluating evidence by favouring views that correspond to their existing attitudes [22]. For example, empirical evidence shows that people rate arguments as more compelling when they correspond to previously held attitudes [23]. In summary, it is likely that interaction does not always lead to assimilation and that social influence is anchored by existing opinions.

This is similar to the approach in [24] but on the traits instead of the features. In general, if the number of features are much higher than the number of traits, there will be consensus, however, bounded confidence has been suggested as a method for compensating for this [11]. Similarly, [25] show that adding influence between those with similar options is sufficient for cultural diversity. A model similar in spirit in [26] uses an open-mindedness parameter, if two clusters are similar then there is higher probability they will coalesce, there is also a probability a group will fragment. This open-mindedness parameter is similar to the bounded confidence threshold. A model, with only binary options for the traits inspired by the Axelrod model with bounded confidence can also lead to multiple clusters [27]. A key difference in the model we present to other approaches that use bounded confidence on the Axelrod model is we take this threshold into account when computing who an agent can interact with, and then again when seeing if they are converted. This only introduces a single parameter and does not restrict the number of traits.

In this paper, we firstly use bipartite network visualisations to identify opinion-based group structure in the standard Axelrod model. Secondly, we introduce an agreement threshold similar to the notion of bounded confidence. Axelrod’s original interaction mechanism was based on the principle of homophily—“the likelihood that a given cultural feature will spread from one individual to another depends on how many other features they may already have in common.” If the nominal traits available to each agent are ordered then there is another dimension for homophily. A small modification to the interaction rules allows us model the types of survey-based data evident in the field of opinion-based groups.

Methods

Standard Axelrod model

In the social sciences, attitudinal surveys are the most common way of measuring individual opinions. We wish to model participants holding attitudes and the groups they form as a result. To do this we start with with Axelrod’s model of cultural diffusion [7]. Here, each agent takes a position on a set of features; and that position must be one of a fixed set of traits. We begin by visualising this model using a bipartite graph—a graph with two types of nodes where edges must connect nodes of different types. One type of node represents the agents and the other represents their trait on a specific feature.

The original Axelrod model on a lattice (without periodic boundary conditions) works as follows: Each individual has a feature set $F = {f_{1}, f_{2}, \dots, f_{F}}$ where f_k is each specific feature. There are a total of $F = dim (F)$ features and each feature f_k has q traits (initially assigned at random). At each time-step, individual i and one of its neighbours j are chosen at random. With a probability equal to the number of common features over the total number of features, person i will copy one of the traits they do not have in common with j.

Fig 1 shows the Axelrod model for 100 nodes on a lattice with F = 3 and q = 5 paused after 40,000 time steps. The absence of a line represents all five features in common, dotted lines represent three or four features in common, dashed lines represent one or two shared features and a thick solid line represents no features in common. When multiple clusters are found, the lattice is divided into regions which are physically separated from each other as seen here. A cluster with no edges indicates that those nodes all have the exact feature configuration.

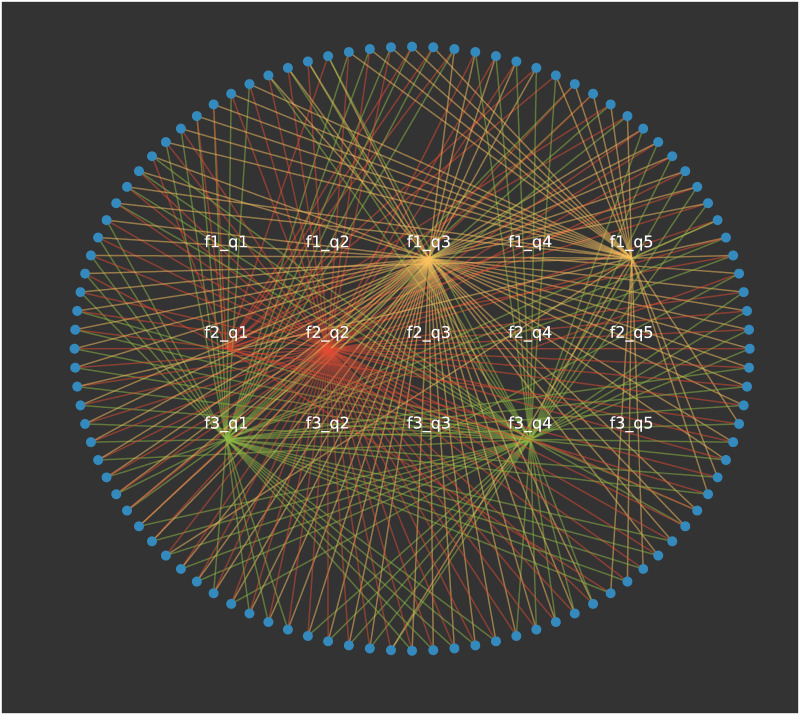
A bipartite network representation of the same data is shown in Fig 2. Here, the underlying feature-trait combinations are revealed, with each feature displayed using a different colour. For example, we observe that features 1 and 2 both have a majority but feature 3 is split between q = 1 and q = 4. This is particularly useful if using this network to represent survey data. If there are three questions with a five-scale response, it is clear which response is the most favoured per question.

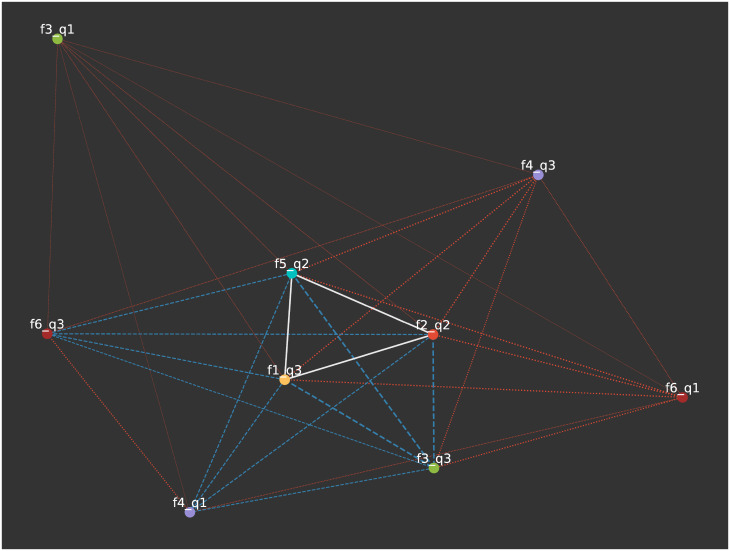
Projections can be taken from this representation to show which feature-trait combinations are frequently held together (see for example Fig 4) and to show the opinion-based groups that form (see Fig 5). In the latter projection, if just full agreement edges are shown (i.e. where the agent share the same traits for each features), this gives the clusters usually discussed. If this is reduced to one minus the full agreement, it will display clusters who agree on all but one trait. An example of this can be seen in Fig 5 where different coloured edges represent different levels of agreement between the clusters.

Fig 5 — Here, two nodes are linked if they hold an attitude in common. White links represent nodes agreeing on all six attitudes, blue edges represent five common attitudes, and red represent three or four.

Agreement thresholds on the traits

One key difference between survey data and the Axelrod model is that in the Axelrod model the traits for a given feature are nominally related (i.e. not ordered) but in survey data the response options are related to one another, or on a scale (e.g., a Likert-type scale) [28]. We introduce a mechanism to allow for traits to be related to each other below.

A shortcoming of using the Axelrod model to represent survey data is a tendency toward uniform convergence in the final state as the number of features increase. Given that attitudes are negotiated properties of social interaction [29], it is plausible to assume that people hold a broad range of continuous positions on a given attitude. However, we are interested in how attitudes are communicated. People typically communicate attitudes verbally, which leads to a certain level of imprecision in their interpretation [30, 31]. We argue that by scaling opinions to a limited number of points on a continuous scale, surveys capture general limitations in attitude communication and interpretation. Furthermore, continuous variable models show a tendency for opinions to move towards the mid-point of the scale [32, 33] and thereby fail to capture the stubbornness of extremists [34].

In the standard Axelrod model above, if two neighbours interact, the node originally chosen copies the state of one of its neighbour’s features that they do not already agree on. We argue that purely copying an attitude of an individual with whom you interact even if you strongly disagree with this attitude is unrealistic. Hence, we introduce an agreement threshold, a, analogous to a latitude of acceptance [29] to compute the interactions. The idea is that there exists a range of positions a person is willing to hold with this range being anchored by their current position within which they copy.

Instead of interacting with someone with probability proportional to the number of common features, we now calculate the probability to interact as the number of features within this agreement threshold over the total number of features, with interaction leading to a copying of one of those traits (i.e., only traits within the agreement threshold can be copied).

Once the state to copy is chosen, it only copies if the difference in values of the chosen feature between interacting individuals i and j is less than the threshold, |f_k,i − f_k,j|≤a. For example, if the threshold is set to the smallest difference between response options in a survey scale, then only those who are one point away from each other on the survey scale will interact.

In contrast with standard Axelrod, here the probability for interaction between two nodes is increased when the agreement threshold is included as features which are a traits away now add to the probability for interaction. However, when interaction occurs, the only features that can change are those within the agreement threshold. In standard Axelrod once interaction happens one feature will be copied, thereby increasing the probability of interaction in the future. In this version only the features which are already within the agreement threshold change, meaning the probability for interaction in the future is the same (unless a trait is changed by a different neighbour).

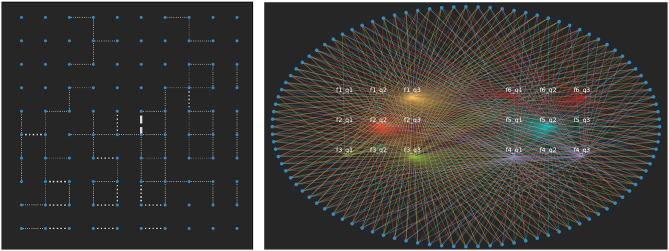
Fig 3 displays the final state for the lattice and bipartite visualisations of this model with F = 6, q = 3 with the lowest possible agreement threshold a = 1. For standard Axelrod, this would lead to consensus, however, here we see we have different regions and from the bipartite representation, half of the six features do not reach consensus. This is a simple adjustment to standard Axelrod that yields more than one cluster even where the number of features exceeds the number of traits per feature as they would in a typical survey.

Projections

Visualising Axelrod on a bipartite space helps us realise that projections can be made to observe the connections between feature-trait combinations and nodes. A 1-mode projection can be generated showing features as nodes with an edge indicating that two features are held concurrently by an agent, and therefore overall which attitudes are strongly connected.

The projection for F = 6, q = 3 is shown in Fig 4 where the weight of an edge is the number of pairs of nodes that share that feature-trait combination. These are split in thirds from weakest to strongest for visualisation purposes. The strongest edges are between the three attitudes where consensus is reached as these are held together most commonly.

Fig 5 shows the 1-mode projection for agents where agents are nodes, linked if they share an attitude in common. The colour of the edge represents how many attitudes they share, and we can identify a number of clusters where they share all six attitudes (with white edges). Note that this figure only displays the giant component. As the edges are created by shared links, if a node has no features in common with any other node, it will not be connected and therefore not appear in any clusters.

Number of clusters

To count the number of clusters, we count the number of components where the nodes agree on all F features in the final state. (Note that for larger systems, and larger agreement thresholds, it can make sense to count clusters that differ by one instead of assuming they all agree, however, here we are just taking the most simplified approach initially).

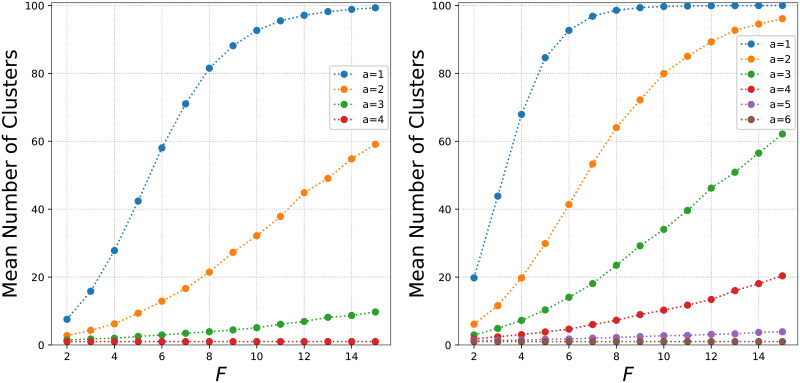
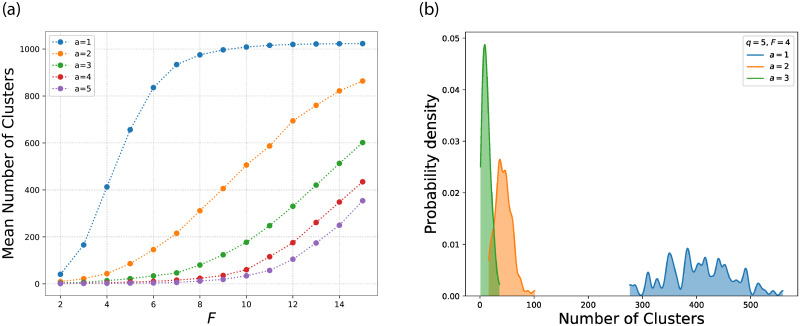
Fig 6 shows the average number of clusters for varying features for the agreement-threshold model with q = 5 (left) and q = 7 (right) for 1,000 runs with 100 nodes. For small a, as F increases the average number of clusters increases as there is a much larger feature-trait space. Due to the large number of different opinion based groups, it is harder for large clusters to form so the cluster size gets smaller. As a increases, there are more conversions and thus less clusters in the final state.

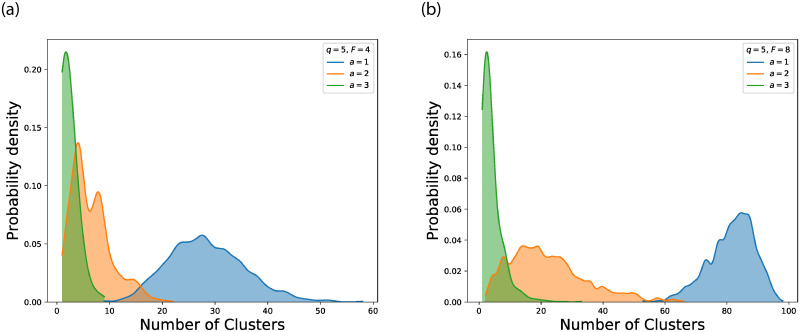
As Fig 6 focussed on the mean of 1,000 runs, we next display the density plot showing the distribution of the number of clusters for one feature in Fig 7. The left panel shows the change in the number of clusters in increasing a with 4 features and 5 traits. In the right panel we increase to 8 features. Again we observe as a increases the number of clusters reduces to as there are more conversions and larger groups. For low agreement thresholds however, there are a much larger number of clusters and with large F, there are very few large clusters with many isolates who don’t have the same feature-trait combination as any other nodes.

Fig 7 — The figure on the left has F = 4 on the right F = 8. As the number of features increases, larger clusters are harder to form as there is a much larger feature-space to agree on.

Finally, in Fig 8 we increase the system size to 1,024 with q = 7. In the left panel we observe the same change in mean number of clusters per feature as in Fig 6. In the right panel, we show the density plot, there is a larger jump between a = 1 and a = 2 when the system size increases.

Note that for agreement threshold a = q − 1, every interaction will lead to copying so this will quickly yield full consensus. Also note that in all these simulations, due to interactions now occurring when agents have a similar trait instead of exactly the same as in standard Axelrod, these tend to reach their final state faster than standard Axelrod.

Conclusion

Here, we added an agreement threshold to the Axelrod model. This threshold yields many clusters for small values of q. This addition is an adjustment to standard Axelrod interaction rules that only allow those with similar features to influence each other. The resulting model is suited to natively modelling survey data, which frequently consists of Likert-type responses, since only ranking and swapping operations are required thus respecting the ordinal nature of the data. The model also avoids the homogoneous end-state which tends to be the case when the standard Axelrod model is used on survey-type data, as there are almost always features than traits (i.e. more items than response options).

In this model, extremists are less likely to change their position than moderates. Due to the agreement threshold, an agent with an attitude on either extreme can only move in one direction, an agent in the middle can move in either direction so is twice as likely change their position. This helps with avoiding a problem some models have causing agents to move towards a centrist attitude and achieving polarisation [35]. This behaviour is also observed in real social systems [34].

Here, this model is entirely theoretical and uses random seeding of the initial system on a regular lattice. Going forward we would like to use empirical data to seed the initial values rather than randomly assign them, something which is used in the following approaches to Axelrod models [11–14].

Further work needs to be done on testing this method on topologies other than a lattice. Similarly, varying q per feature should be tested as there is no reason the number of traits per feature should be the same. This last suggestion is made in [11]. A further extension could specify that if the agreement threshold is larger than one, the traits move towards each other rather than one agent copying the other. We also wish to relax the rules for group membership, here we took groups where everyone agrees with everyone, however, going forward we wish to investigate this with agreement on a smaller number of core attitudes. In this case we would get larger clusters similar to when F is in the middle range of Fig 6.

Future work will seed this extended Axelrod model with real survey data to compare the sensitivity or resilience of various real-world attitude network topologies to cultural diffusion. We expect that it will be relatively straightforward to make similar modifications to other opinion dynamics models to allow the consideration of survey-type data.

The code to run bipartite simulations and the agreement threshold can be found here: https://github.com/pmaccarron/Agreement-Threshold-Axelrod.

Acknowledgments

The authors would like to thank the attendees of the workshop “ToRealSim meets DAFINET: Linking agent based models with empirical evidence”, 4-6 April 2019, University of Limerick, Ireland. In particular the authors thank Michael Mäs, Sylvie Huet and Guillaume Deffuant for their detailed feedback on this manuscript.

Data Availability

The data is generated randomly using the model presented in the paper.

Funding Statement

PMC, PM and MQ are funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 802421: https://ec.europa.eu/programmes/horizon2020/en/h2020-section/european-research-council SF, KB and JPG are funded by the the Irish Research Council (SF) and from Science Foundation Ireland (JPG, grant numbers 16/IA/4470 and SFI/12/RC/2289P2: http://research.ie/https://www.sfi.ie/ The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

1. Festinger L. A theory of social comparison processes. Human relations. 1954;7(2):117–140. 10.1177/001872675400700202 [DOI] [Google Scholar]
2. Lewin K. Group discussion and social change. Basic Studies in Social Psychology New York: Holt, Rinehart and Winston. 1947;1965. [Google Scholar]
3. Tajfel H, Turner JC, Austin WG, Worchel S. An integrative theory of intergroup conflict. Organizational identity: A reader. 1979; p. 56–65. [Google Scholar]
4. Bar-Tal D. Group beliefs: A conception for analyzing group structure, processes, and behavior. Springer Science & Business Media; 2012. [Google Scholar]
5. Kruglanski AW, Pierro A, Mannetti L, De Grada E. Groups as epistemic providers: need for closure and the unfolding of group-centrism. Psychological review. 2006;113(1):84. [DOI] [PubMed] [Google Scholar]
6. Bliuc AM, McGarty C, Reynolds K, Muntele D. Opinion-based group membership as a predictor of commitment to political action. European Journal of Social Psychology. 2007;37(1):19–32. 10.1002/ejsp.334 [DOI] [Google Scholar]
7. Axelrod R. The dissemination of culture: A model with local convergence and global polarization. Journal of conflict resolution. 1997;41(2):203–226. 10.1177/0022002797041002001 [DOI] [Google Scholar]
8. Kero P, Lee D. Likert is Pronounced “LICK-urt” not “LIE-kurt” and the Data are Ordinal not Interval. Journal of applied measurement. 2016;17(4):502–509. [PubMed] [Google Scholar]
9. Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Reviews of modern physics. 2009;81(2):591 10.1103/RevModPhys.81.591 [DOI] [Google Scholar]
10. Boyd R, Richerson PJ. The origin and evolution of cultures. Oxford University Press; 2005. [Google Scholar]
11. Valori L, Picciolo F, Allansdottir A, Garlaschelli D. Reconciling long-term cultural diversity and short-term collective social behavior. Proceedings of the National Academy of Sciences. 2012;109(4):1068–1073. 10.1073/pnas.1109514109 [DOI] [PMC free article] [PubMed] [Google Scholar]
12. Băbeanu AI, van de Vis J, Garlaschelli D. Ultrametricity increases the predictability of cultural dynamics. New Journal of Physics. 2018;20(10):103026 10.1088/1367-2630/aae566 [DOI] [Google Scholar]
13. Băbeanu AI, Talman L, Garlaschelli D. Signs of universality in the structure of culture. The European Physical Journal B. 2017;90(12):237 10.1140/epjb/e2017-80337-7 [DOI] [Google Scholar]
14. Stivala A, Robins G, Kashima Y, Kirley M. Ultrametric distribution of culture vectors in an extended Axelrod model of cultural dissemination. Scientific reports. 2014;4:4870. [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Klemm K, Eguíluz VM, Toral R, San Miguel M. Global culture: A noise-induced transition in finite systems. Physical Review E. 2003;67(4):045101 10.1103/PhysRevE.67.045101 [DOI] [PubMed] [Google Scholar]
16. Klemm K, Eguíluz VM, Toral R, San Miguel M. Nonequilibrium transitions in complex networks: A model of social interaction. Physical Review E. 2003;67(2):026120 10.1103/PhysRevE.67.026120 [DOI] [PubMed] [Google Scholar]
17.Mazzitello KI, Candia J, Dossetti V. Effects of Mass Media and Cultural Drift in a Nonequilibrium Model for Social Influence; 2006. physics/0611189. Available from: http://cds.cern.ch/record/1000329.
18. Battiston F, Nicosia V, Latora V, San Miguel M. Layered social influence promotes multiculturality in the Axelrod model. Scientific reports. 2017;7(1):1809 10.1038/s41598-017-02040-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Flache A, Macy MW. Why more contact may increase cultural polarization. arXiv preprint physics/0604196. 2006;.
20. Deffuant G, Neau D, Amblard F, Weisbuch G. Mixing beliefs among interacting agents. Advances in Complex Systems. 2000;3(01n04):87–98. 10.1142/S0219525900000078 [DOI] [Google Scholar]
21. Hegselmann R, Krause U, et al. Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of artificial societies and social simulation. 2002;5(3). [Google Scholar]
22. Lord CG, Ross L, Lepper MR. Biased assimilation and attitude polarization: The effects of prior theories on subsequently considered evidence. Journal of personality and social psychology. 1979;37(11):2098 10.1037/0022-3514.37.11.2098 [DOI] [Google Scholar]
23. Taber CS, Lodge M. Motivated skepticism in the evaluation of political beliefs. American journal of political science. 2006;50(3):755–769. 10.1111/j.1540-5907.2006.00214.x [DOI] [Google Scholar]
24. De Sanctis L, Galla T. Effects of noise and confidence thresholds in nominal and metric Axelrod dynamics of social influence. Physical Review E. 2009;79(4):046108 10.1103/PhysRevE.79.046108 [DOI] [PubMed] [Google Scholar]
25. Flache A, Macy MW. Local convergence and global diversity: From interpersonal to social influence. Journal of Conflict Resolution. 2011;55(6):970–995. 10.1177/0022002711414371 [DOI] [Google Scholar]
26. Apolloni A, Gargiulo F. DIFFUSION PROCESSES THROUGH SOCIAL GROUPS’DYNAMICS. Advances in Complex Systems. 2011;14(02):151–167. 10.1142/S0219525911003037 [DOI] [Google Scholar]
27.Martin S, Deffuant G, Nadal JP, Weisbuch G. Comparing the binary opinion vector version of the BC model with different approximating aggregated dynamics. M2M Workshop. 2004;.
28. DeVellis RF. Scale development: theory and applications Applied social research methods series. Thousand Oaks: Sage Publications, Inc.; 2003. [Google Scholar]
29. Sherif M, Hovland CI. Social judgment: Assimilation and contrast effects in communication and attitude change. Yale Univer. Press; 1961. [DOI] [PubMed] [Google Scholar]
30. Pierro A, Mannetti L, Kruglanski AW, Sleeth-Keppler D. Relevance override: on the reduced impact of “cues” under high-motivation conditions of persuasion studies. Journal of Personality and Social Psychology. 2004;86(2):251. [DOI] [PubMed] [Google Scholar]
31. Teigen KH. The language of uncertainty. Acta Psychologica. 1988;68(1):27–38. 10.1016/0001-6918(88)90043-1. [DOI] [Google Scholar]
32.Flache A, Macy MW. What sustains cultural diversity and what undermines it? Axelrod and beyond. arXiv preprint physics/0604201. 2006;.
33. Mäs M, Flache A. Differentiation without distancing. Explaining bi-polarization of opinions without negative influence. PloS one. 2013;8(11):e74516 10.1371/journal.pone.0074516 [DOI] [PMC free article] [PubMed] [Google Scholar]
34. Brandt MJ, Evans AM, Crawford JT. The unthinking or confident extremist? Political extremists are more likely than moderates to reject experimenter-generated anchors. Psychological Science. 2015;26(2):189–202. 10.1177/0956797614559730 [DOI] [PubMed] [Google Scholar]
35. Flache A, Mäs M, Feliciani T, Chattoe-Brown E, Deffuant G, Huet S, et al. Models of Social Influence: Towards the Next Frontiers. Journal of Artificial Societies and Social Simulation. 2017;20(4):2 10.18564/jasss.3521 [DOI] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0233995.r001

Decision Letter 0

Carlos Gracia-Lázaro

17 Dec 2019

PONE-D-19-31281

Agreement Threshold on Axelrod's model of Cultural Dissemination

PLOS ONE

Dear Dr. Mac Carron,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

We would appreciate receiving your revised manuscript by Jan 26 2020 11:59PM. When you are ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter.

To enhance the reproducibility of your results, we recommend that if applicable you deposit your laboratory protocols in protocols.io, where a protocol can be assigned its own identifier (DOI) such that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). This letter should be uploaded as separate file and labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. This file should be uploaded as separate file and labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. This file should be uploaded as separate file and labeled 'Manuscript'.

Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out.

We look forward to receiving your revised manuscript.

Kind regards,

Carlos Gracia-Lázaro

Academic Editor

PLOS ONE

When submitting your revision, we need you to address these additional requirements:

Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at http://www.plosone.org/attachments/PLOSOne_formatting_sample_main_body.pdf and http://www.plosone.org/attachments/PLOSOne_formatting_sample_title_authors_affiliations.pdf

Additional Editor Comments (if provided):

The authors should pay attention to the reviewers' suggestions inviting to a deep revision of the manuscript both in its form and in its content and methods.

Also, the authors should pay attention to the journal's criteria of code availability.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

Reviewer #2: Partly

Reviewer #3: No

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: No

Reviewer #2: N/A

Reviewer #3: No

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: No

Reviewer #3: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: PONE-D-19-31281

Agreement Threshold on Axelrod's model of Cultural Dissemination

The manuscript contains two distinct contributions regarding the well-known Axelrod model of cultural dissemination. First, a visualization technique based on representing the system as a bipartite graph where the two node types are agents and traits (specifically one node for each trait value in each feature so there are qF such nodes using the usual notation of F for the feature vector dimension and q for the number of trait values). The one-mode projections of this graph can then be used to show connections between attitudes (where nodes are the traits) or connections between agents with common attitudes (where nodes are the agents).

The second aspect of the manuscript is the introduction of an "agreement threshold" based on the social judgment theory concept of "latitude of acceptance". The Axelrod model is modified so that the probability of interaction is no longer proportional simply to cultural similarity (Hamming distance between culture vectors) but instead proportional to the number of features within the agreement threshold a. (Note that this depends on the traits now being treated as ordinal rather than categorical [nominal]). Further, rather than any randomly chosen trait (not already equal) being copied, only a trait within the agreement threshold is copied.

Although the manuscript is a potentially useful contribution, I think points 1, 2, and 9 below need to be addressed before it could published (the other points are more minor, or not a barrier to publication PLOS ONE).

1. I think there is insufficient consideration of the existing literature, which is rather extensive for the Axelrod model and various enhancements or modifications of it. There are some reviews of this literature, and two are cited (citations [28] and [29], Flache et al. (2017) and Castallano et al. (2009)), but these reviews are not necessarily exhaustive of the (very extensive) literature on the Axelrod model (and the longer review article is 10 years old).

In particular, although some of the Flache & Macy arXiv preprints introducing it are cited, I would have expected more discussion of "bounded confidence" as it is so closely related to the "agreement threshold" idea, and in particular, De Sanctis & Galla (2009) and Hegselmann & Krause (2002) are good sources for this (the latter is not about the Axelrod model, but gives some citations for the history of the "bounded confidence" idea in other models). Another very useful paper on the Axelrod model is Flache & Macy (2011), who state that:

"The bounded confidence models showed that global diversity does not depend on the assumption that opinions are discrete, as long as influence can only occur between individuals who are sufficiently similar. Thus, while Axelrod introduced two innovations—discrete opinions and homophily — these subsequent studies showed that the latter is sufficient for local convergence to preserve global diversity."

(Flache & Macy (2011), p. 972).

These papers are all cited in the Flache et al. (2017) review, which discusses bounded confidence, but I think it is necessary to do more than just cite the review in this manuscript, and actually also directly cite the individual papers and discuss bounded confidence and its relationship to the "agreement threshold".

These omissions can be easily rectified, but in such an extensively studied topic as the Axelrod model, with many variations and in different literatures (political science, physics, social psychology, etc.) it is easy to overlook relevant work and inadvertently re-invent something or fail to cite directly relevant prior work, so I believe it is particularly important to be thorough in this area.

This has particular relevance to my next point, as I think the highly relevant paper Valori et al. (2012) needs to be considered.

2. The main motivation is to use survey data with ordinal scales (e.g. Likert scales) in the Axelrod model. However (related to point 1 above) this has already been done in published literature, which is not cited in the manuscript. Specifically, Valori et al. (2012) use an Axelrod model with empirical data from surveys as the initial culture vectors (rather than the usual random initialization), as do some subsequent works, for example Babeanu et al. (2017) [see Appendix A for details of treatment of survey data with nominal and ordinal cultural features]; Babeanu et al. (2018); Stivala et al. (2014).

The details of this in the Valori et al. (2012) paper are largely in the Supplementary Information, but they are there (see S.I. p. 3), showing how both nominal and ordinal features are treated in their version of the Axelrod model. Even some of the "further work" in the manuscript such as "vary q per feature" is already implicitly described there.

In addition, the Valori et al. (2012) S.I. discusses the arbitrariness of the number of features F and how bounded confidence can compensate for this (see SI. pp. 6-7 and footnote on p. 7), which was a motivation in the manuscript for introducing the agreement threshold.

3. Similarly, although I am not familiar with any previous publications using the bipartite graph idea, the one-mode projection where nodes are agents would appear to be a weighted version of the "cultural graph" described by Valori et al. (2012), in which an edge exists between agents with sufficiently similar (according to the value of the confidence threshold) culture vectors. Although in Valori et al. (2012) and subsequent work building on it the "cultural graph" was not used for visualization, it nevertheless was defined and used for analysis of the model.

4. I am not convinced of the utility of the bipartite graph visualization (e.g. Fig. 2). It seems to me that the presence of the agents as nodes and the density of lines showing the feature-trait combinations really just clutters the visualization (and would quickly become unreadable for larger values of N, q, and F). Would it not be simpler just to represent the relative proportions of the feature-trait combination as a heat map, for example? Valori et al. (2012) visualize correlations between opinions as heat maps and dendrograms (as they are interested in the structure of such correlations), but the simple proportions of each trait could also be visualized directly this way.

5. Although I believe the "agreement threshold" is a new and useful contribution, I found its explanation a little confusing at first. I think it might be clearer to specify it not just in English but also precisely in mathematical notation, as is done in the physics literature on the Axelrod model for describing the measure of cultural similarity etc. In the abstract (where mathematical notation is inappropriate) on a first reading it seemed to me that the "agreement threshold" was just the same as "bounded confidence", and it required reading the manuscript carefully to see that it is not.

6. On p. 2 "Specifically, when the number of features F is greater than the number of traits q , usually there will be consensus with only one cluster emerging [8]". I'm not sure that this statement is supported by citation [8] (Castellano et al. (2000)). [See point (2) above for more on how the arbitrariness of the number of features F has previously been handled for survey data using bounded confidence.]

7. Why is the number of clusters counted with the "dispersion indicator" rather than a more conventional order parameter for the Axelrod model such as the mean size of the largest cluster, or simply the number of cultures? There is a mention of phase transitions as further work in the Conclusions section, and indeed no phase transition is apparent in Fig. 6. Presumably this is because the quantity on the x axis does not control a phase transition (while q does, for example). Or perhaps is the "dispersion indicator" actually not an order parameter?

8. I found Figure 6 (or more precisely its axis labeling) confusing. What is the x axis exactly? It is labeled "No. features" so it seems to be the dimension of the culture vector i.e. F. If so I think it would be better to clearly state this. [There is also a typo in the caption, should be q = 7 not q - 7].

9. I don't think the computational experiments are thorough enough. In the absence of any analytical treatment (mean-field approximation for example) simulation experiments are all that can be done, which is reasonable. However the only computational experiments seem to be those represented in Figure 6 showing the dispersion indicator in the absorbing state (final state) for two values of q (and the corresponding possible values of a) and one value of N. There are no error bars so it would seem these represent just a single run of the model for each parameter combination. At a minimum I would expect the results of multiple runs (from random initial conditions) and the figure then showing the mean and standard deviation (or 95% confidence interval) over many runs, as is done in the vast majority of publications on Axelrod model variants.

10. The manuscript defines a bipartite network as "a network with two types of nodes" (p. 2) but omits the essential point that any edge must be between nodes of two different types (never two nodes of the same type). Indeed a bipartite graph is conventionally defined as a graph in which the nodes can be partitioned into two disjoint sets such that every edge connects a node in one set to a node in the other.

11. Although PLOS ONE requires data be made freely available, it appears to have no such requirement for code. Hence I cannot insist that the code for the modified Axelrod model with agreement threshold be made available, nevertheless I think it would be preferable to do so to facilitate reproducbility. Even a "toy" version in e.g. NetLogo would allow people to verify their undertanding of the model description in the manuscript (see also point (5) above) or compare their own implementation to check they match.

References (in addition to those cited in the manuscript)

Băbeanu, A. I., Talman, L., & Garlaschelli, D. (2017). Signs of universality in the structure of culture. The European Physical Journal B, 90(12), 237.

Băbeanu, A. I., van de Vis, J., & Garlaschelli, D. (2018). Ultrametricity increases the predictability of cultural dynamics. New Journal of Physics, 20(10), 103026.

De Sanctis, L., & Galla, T. (2009). Effects of noise and confidence thresholds in nominal and metric Axelrod dynamics of social influence. Physical Review E, 79(4), 046108.

Flache, A., & Macy, M. W. (2011). Local convergence and global diversity: From interpersonal to social influence. Journal of Conflict Resolution, 55(6), 970-995.

Hegselmann, R., & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of artificial societies and social simulation, 5(3).

Stivala, A., Robins, G., Kashima, Y., & Kirley, M. (2014). Ultrametric distribution of culture vectors in an extended Axelrod model of cultural dissemination. Scientific reports, 4, 4870.

Valori, L., Picciolo, F., Allansdottir, A., & Garlaschelli, D. (2012). Reconciling long-term cultural diversity and short-term collective social behavior. Proceedings of the National Academy of Sciences, 109(4), 1068-1073.

Reviewer #2: Please see attached review report.....................................................................................................................................................................................................................................................................................

Reviewer #3: In this paper, the authors propose modifications to the Axelrod model. This work supposedly has two contributions: a method for displaying the system state through a bipartite network, and a modification in the step which defines how agents interact.

It is unclear if the method for displaying the system state as a bipartite graph provides any benefit. For instance, the conclusions they reach through Figure 2 would be easier to observe through a usual frequency plot. Furthermore, the figures provide a poor visualization of the bipartite graph and it is difficult to see where are the traits nodes. If there was some benefit in the bipartite representation they should make use of this representation to achieve something that would not be possible without a network, e.g., finding communities or computing distances. This is not the case in this paper.

Lastly, their modification to the Axelrod model is not explored seriously. Results are analysed in terms of individual executions without any clear demonstration of how representative they are. Fig. 6 seems to be the only one corresponding to ensemble averages, however, it lacks statistical information. As they posed in the conclusion, it is necessary to analyse the change of behaviour for different values of F, q, a, and N. Furthermore, their most remarkable conclusion is concerning the different expectations for the number of clusters in the final states. However, according to the authors model, when agents interact, only the features that have traits within the agreement threshold can be copied. This behaviour can make some features never being copied, which would lead to a final state without consensus. Therefore, their finding of "a large number of clusters" might be an effect of this limitation and not the agreement threshold.

Specific remarks

- Fig. 1 and 2 supposedly correspond to a simulation with F=3 and q=5. However, the authors explain the visualization for F=5.

- Authors refer to the paper for attitudes and response-options, but it is not clear how they are related to features or traits. Do attitudes correspond to the number of traits or features?

- To verify the number of clusters in the simulation, the authors use the dispersion indicator. However, if the goal is to count the number of clusters, wouldn't be more natural to check directly the number of clusters?

- Some phrases of the manuscript are really hard to understand and the authors should work on the writing, e.g., line 180.

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

Reviewer #3: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files to be viewed.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email us at figures@plos.org. Please note that Supporting Information files do not need this step.

Attachment

Submitted filename: PlosOne_review_2019.pdf

Click here for additional data file.^{(82.8KB, pdf)}

PLoS One. 2020 Jun 2;15(6):e0233995. doi: 10.1371/journal.pone.0233995.r002

Author response to Decision Letter 0

27 Mar 2020

Reviewer #1

Reply: Thanks for this, we have added more references and expanded the introduction (in red) and are happy to add more or expand more on this if necessary.

(Flache & Macy (2011), p. 972).

Reply: Bounded confidence was the main reason we came up with this model so was a big influence, however, we removed this after multiple discussions from those mentioned in the acknowledgements. Their argument was that with the traits and bound not being continuous it was too confusing to call it bounded confidence when we were dealing with discrete values – even though there are models out there that take discrete values. Also you’ll see at one point we discuss something about not using continuous values, the survey discussion was added in after to convince them that taking discrete values had merit. Initially this paper was framed more theoretically in terms of adding this bounded confidence extension (which we later renamed an agreement threshold), we added the survey framing after their comments.

Reply: Many thanks for this, though familiar with the paper I confess I had not looked at the SI. We have added this to the introduction now and again are happy to elaborate further if necessary.

Reply: We have added a sentence on this.

Reply: For pure Axelrod as the feature-trait combination are arbitrary it can look strange, however increasing in size won’t be a problem as the brightness increases. However, out main interest in this type of visualisation will come when we actually apply it to survey data, see this image for example:

https://www.dropbox.com/s/d8zv783gf4ijy19/attitudes_net_2113_kk.png?dl=0

The two types of nodes are people and their responses to eight questions, as the features (questions) and traits (responses) are no longer arbitrary we think it’s a nice way to visualise this type of data which is why we included it here. We decided we wanted to keep this paper theoretical though so did not add the empirical data.

Reply: We have added an equation to the section now.

Reply: Perhaps this is better phrased as multicultularity is found for very high numbers of q are required but in out work we have a small value (5 or 7 typically). We have edited this and added that bounded confidence was suggested as a fix for this.

Reply: We initially used cluster size but were recommended the dispersion indicator, however we are happy to go back to number of clusters. We went with the mean (of 1000 simulations) and rather than use standard deviation or the 5 and 95 percentile, we instead show another figure with the density plot of a specific q and F varying the agreement threshold to get an idea of effect of the changing parameters and the distributions are clearer to see than with error bars in the plot for the means. (Note we have done it with the error bars but feel there is a bit too much going on, see:

https://www.dropbox.com/s/c2x1gb5x2nj3phs/n_clusters_95_percentile.png?dl=0

however, we are happy to put this in also if necessary).

There is a mention of phase transitions as further work in the Conclusions section, and indeed no phase transition is apparent in Fig. 6. Presumably this is because the quantity on the x axis does not control a phase transition (while q does, for example). Or perhaps is the "dispersion indicator" actually not an order parameter?

Reply: We removed the dispersion index as, although we were recommended to use it, we didn’t really understand it clearly. We also removed mention of a phase transition.

Reply: Thanks, we have edited this now.

Reply: We have changed to the mean number of clusters and provide the density plots as well as do this for both N = 100 and N = 1024 now. Also we have made it more clear that each point represents 1,000 simulations and expanded on the discussion in that section.

Reply: We have put in that edges have to connect different types of nodes now to clarify this.

Reply: The code was written in Python so I have uploaded a script to my github and linked at the end.

Reviewer #2

1) The code to run the simulations and to produce the novel plots presented in the

manuscript is not made available. No one can evaluate the results of the model without the

code. Importantly, the new plotting techniques are a potentially valuable contribution of the

manuscript. However readers interested in using these methods are forced to figure out how

to implement them on their own. I would recommend writing the ABM and the plotting

scripts in R, as this would make these innovations accessible to a broad range of researchers

from different disciplines.

Reply: The code was written in Python so I have uploaded a script to my github and put the link at the end.

I found Figure 1 to be confusing. Because nodes are connected with lines representing

their similarity, it was difficult for me to discern the boundaries between clusters. Instead,

I would recommend using lines in the spaces around nodes (rather than lines connecting

nodes) to represent similarity/difference, and presenting a time series of plots so that read-

ers can see the clusters develop over time. In other words, model your figure after the original

Axelrod (1997) Figure 1.

Reply: The reason we chose to do it this way is on the next figure we want to represent a node as an agent in the bipartite graph. Then there is a connection between that node and its attitude, if we use the “site” which is what is traditionally done then it is hard to translate that to a node when connecting it to the attitude. We have put in a statement on this hopefully making it less confusing.

3) I don’t understand the interpretation given for the dispersion parameter d in equation

1. It seems that d is equivalent to n in equation 9 of the cited reference (Duffuant 2006),

which is the “generalized number of clusters” according to this reference. However, in the

manuscript it is stated that the inverse of d represents the generalized number of clusters

(lines 154-155). Similarly, it is stated that Figure 6 plots d, which does seem to be the inverse

of the number of clusters. Am I correct that what you have actually plotted in Figure 6 is

1/d?

4) I don’t understand the explanation for why adding an agreement threshold a results in

an increasing number of clusters at equilibrium as the number of features (F ) increases. The

explanation given on lines 160-162 is: “As the number of features increases, there are a larger

number of feature-trait combinations an agent can have. For a low agreement threshold an

agent would not be able to interact with any of its neighbours.” If I understand correctly

what is written, this process serves to increase the number of isolated nodes at equilibrium,

which in turn contributes to a larger number of clusters. However, this runs counter to

my intuition. It’s quite possible that I have misunderstood something about the model, so

I will outline my thinking below. If there is some error in my logic, perhaps the authors

would consider including some additional explanation in the paper so that readers don’t

make similar mistakes.

Reply: The agreement threshold is used in the copying of traits as well as in the calculation of a probability for interaction.

The probability for interaction between two nodes is increased when the agreement threshold is included (vs standard Axelrod) as features in which you are (for example) 1 trait away from each other now add to the probability for interaction. However, once you decide interaction can occur, the only features you can change are the ones in which the traits are sufficiently similar (within the agreement threshold). In standard Axelrod once interaction happens one feature will be copied, thereby increasing the probability of interaction in the future. In our version you only change the features which are already quite similar, meaning the probability for interaction in the future is the same.

We have added something on this hopefully clarifying it further but are happy to add more if necessary.

Reviewer #3

Specific remarks

- Authors refer to the paper for attitudes and response-options, but it is not clear how they are related to features or traits. Do attitudes correspond to the number of traits or features?

Reply: We mean the combination, if on a survey your response to question 1 is: 3, then your attitude is question1-response3.

Reply: We have changed to the number of clusters and provide the density plot to visualise the distribution.

- Some phrases of the manuscript are really hard to understand and the authors should work on the writing, e.g., line 180.

Reply: Line 180 for us is in the acknowledgements, however we have cleared up many sentences as highlighted in the text.

Attachment

Submitted filename: response.pdf

Click here for additional data file.^{(36.9KB, pdf)}

PLoS One. doi: 10.1371/journal.pone.0233995.r003

Decision Letter 1

Carlos Gracia-Lázaro

12 Apr 2020

PONE-D-19-31281R1

Agreement Threshold on Axelrod's model of Cultural Dissemination

PLOS ONE

Dear Dr. Mac Carron,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

We would appreciate receiving your revised manuscript by May 27 2020 11:59PM. When you are ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). This letter should be uploaded as separate file and labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. This file should be uploaded as separate file and labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. This file should be uploaded as separate file and labeled 'Manuscript'.

We look forward to receiving your revised manuscript.

Kind regards,

Carlos Gracia-Lázaro

Academic Editor

PLOS ONE

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

Reviewer #2: (No Response)

Reviewer #3: (No Response)

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: No

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

6. Review Comments to the Author

Reviewer #1: PONE-D-19-31281R1

Agreement Threshold on Axelrod's model of Cultural Dissemination

Revision 1 (after first round of review)

The authors have addressed all my concerns and the revised manuscript is now acceptable for publication, in my opinion.

In particular, noting that the results in the figures are means over 1000 runs is very important, as it did appear in the original manuscript that these were single runs. I agree that the plots with error bars (as shown in the Dropbox link in the response) are unreadable, so showing the PDF in a separate figure rather than adding error bars is better.

I now understand the authors' reasoning about the bipartite graph visualizations and this being a theoretical rather than empirical paper, but in a way it is a shame that the survey data figure (Dropbox link from response to my point 4) is not in the paper instead of Fig 2 and Fig 3 (right), as I think the layout of the survey response figure (with the respondent nodes in the centre and the opinions on the outside) is clearer, and the concreteness of the opinions ("Race relations anti" etc.) makes the meaning a lot clearer than "f1_q1" etc. Presumably this will be for a future paper, however.

I am also pleased that the code is now publicly available. I briefly tried it and it found it to work as expected (after changing the output file type as I could not get Matplotlib, which I always have problems with, to work with MPEG on my system).

However, regarding my point (10) on defining "bipartite network", the revised text (at lines 76-77, page 3) now has

"... a network with two types of nodes which cannot have edges connecting

the different types of nodes."

which to my mind is confusing or ambiguous: the essential point is that no edge can join two nodes of the same type. This new sentence, however, could be interpreted as saying just the opposite (that no edge can join two nodes of different types). So I would suggest re-phrasing this sentence to make it clearer.

Reviewer #2: For the most part, I believe my previous comments have been adequately addressed and I would now recommend this manuscript for publication. I have two minor suggestions:

1) The authors' response in the Response to Reviewers letter to Reviewer 2 point #4 was very helpful for me. I would suggest putting that response directly into the manuscript.

2) In Methods: Standard Axelrod Model, penultimate sentence in first paragraph. I think it would be clearer to say "edges must connect nodes of different types"

Reviewer #3: 1. I believe the authors have not provided an appropriate response to the comments made by myself and by reviewer 1 about the usefulness of the graph bipartite representation. According to their comment on line 93: "For example, we observe that features 1 and 2 both have a majority but feature 3 is split between q = 1 and q = 4. This is particularly useful if using this network to represent survey data. If there are three questions with a five-scale response, it is clear which response is the most favoured per question." The authors are reaching this conclusion through the degree of the nodes in the graph plot, which would be a lot clearer in a simple plot showing the frequency of traits per feature. Besides this, I don't see any benefit provided by the bipartite representation and don't believe it is a contribution of the paper. For it to be a contribution, the authors should have used it for some analysis that needed the network representation. Now, it seems to be a rather unnecessary artefact.

2. Still regarding the bipartite representation, the authors mention in the abstract: "This visualisation is particularly useful when representing survey data as it illustrates the coevolution of cultures and opinion-based groups in Axelrod’s model of cultural diffusion." In the introduction, however, authors mention: "Opinion-based groups (or “cultures”) are formed by people holding a particular selection of attitudes." It seems, thus, that cultures and opinion-based groups correspond to the same concept. What would they refer to when discussing about coevolution? Furthermore, it is unclear how this visualization illustrates the supposed coevolution as it is just a representation of the stationary state.

3. Intuitively, it makes sense the use of the agreement thresholds for computing the probability of interaction between agents. Nonetheless, its use in the process of social influence, i.e., copying traits of features that are in the agreement threshold, seems rather unnatural. The authors should add some reference justifying why social influence should only occur in features that are $a$ traits away. Furthermore, this characteristic of the model should be the motive it does not reach consensus for small q and a, as consensus can be unreachable from initialization.

4. In the conclusions, the authors mention: " The

clustering that emerges is useful for considering opinion-based groups in opinion

dynamics models and empirical data such as surveys. " It is unclear how the clusters found in this model can be useful for the applications mentioned. The authors should discuss this more thoroughly.

5. On line 192: "One outcome of this model is that extremists are less likely to change their position

than moderates." This is not an outcome of the model, this is given by the specification of the model. If agents cannot copy the features which are not in the agreement threshold, features with extreme value traits cannot be modified unless the agent's neighbours features are also in the same extreme.

Specific remarks:

- The authors update the definition of the bipartite network according to the comment of reviewer 1, however, the definition still is not precisely correct.

- What is the total number of agents, F, q in the simulations of figure 5?

- "A further extension could specify that if the agreement threshold is larger than one, the traits move towards each other rather than one agent copying the other." This actually could be used without the restraint posed by the initial condition of the model, i.e., of only copying features which are inside the agreement threshold. In my opinion, this makes more sense than the current approach.

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

Reviewer #3: No

PLoS One. 2020 Jun 2;15(6):e0233995. doi: 10.1371/journal.pone.0233995.r004

Author response to Decision Letter 1

23 Apr 2020

Reply: We have added in a paragraph about taking projections from the bipartite representation which is what the figures with clusters represent to show that this is relevant later, for example figures 4 and 5 are projections from the bipartite graph in figure 3. This is subtly different to cultures in standard Axelrod (see response to point 2 for more details) as here a cluster represents groups of people who fully agree, they do not need to be separated. In figure 1 if the lower left and upper right regions have the same traits for each feature in standard Axelrod then they would be two cultures, using the bipartite projection, they would be one opinion-based group. We have added text to clarify this.

We appreciate from a model point of view this can look strange, but from an empirical point of view this is a different way of viewing survey data. For example, the image we mentioned to Reviewer #1 in the first review:

https://www.dropbox.com/s/d8zv783gf4ijy19/attitudes_net_2113_kk.png?dl=0

shows a survey with two types of nodes being the participants and their responses to eight questions, as the features (questions) and traits (responses) are no longer arbitrary we think it’s a nice way to visualise this type of data which is why we included it here. We decided we wanted to keep this paper theoretical though so did not add the empirical data.

This is something from our upcoming empirical paper which we do not really want to include here, we would also like to use this agreement threshold model on empirical data after which is why we would rather leave this bipartite visualisation in.

Reply: This is an important point that we didn’t properly distinguish between. In Axelrod (1997), a culture in the model is a group of agents sharing the same traits for each feature that are physically next to one another. Here, however, as we take a projection from the bipartite graph, the cluster of those who agree entirely are an opinion-based group even if they are physically separated. We have made this more clear in the text by including the line:

We remove this spatial constraint when identifying clusters and instead get groups of agents sharing the same traits for each feature, we refer to these as opinion-based groups.

Reply: Thank you for pointing this out. We had previously included references justifying this feature of social influence, that have now been re-added in the introduction. Further justification is that people tend to display bias in evaluating evidence by favouring views that correspond to their existing attitudes (Lord, ross & Lepper, 1979; Reedy, Wells & Gastil, 2014). For example, empirical research shows that people rate arguments as more compelling when they correspond to previously held attitudes (Taber & Lodge, 2006). The mechanism at play may be biased information processing (i.e. confirmation bias), rather than social influence per se. Either way, we believe it should be accounted for in models of opinion sharing, as indeed it is in many others (Deffuant et al., 2000; Hegselmann et al., 2002). A section similar to this has been added to the introduction.

Taber, C. S., & Lodge, M. (2006). Motivated skepticism in the evaluation of political beliefs. American Journal of Political Science, 50 (3), 755–769.

Reedy, J., Wells, C. and Gastil, J. (2014), How Voters Become Misinformed: An Investigation of the Emergence and Consequences of False Factual Beliefs*. Social Science Quarterly, 95: 1399-1418. doi:10.1111/ssqu.12102

Lord, C. G., Ross, L., & Lepper, M. R. (1979) Biased assimilation and attitude polarization: The effects of prior theories on subsequently considered evidence. Journal of Personality and Social Psychology, 37(11), 2098–2109. https://doi.org/10.1037/0022-3514.37.11.2098

Deffuant G, Neau D, Amblard F, Weisbuch G (2000), Mixing beliefs among interacting

agents. Advances in Complex Systems. 01n04), 7–98.

Hegselmann R, Krause U, et al. (2002), Opinion dynamics and bounded confidence

models, analysis, and simulation. Journal of artificial societies and social

simulation. 5,3.

4. In the conclusions, the authors mention: " The clustering that emerges is useful for considering opinion-based groups in opinion dynamics models and empirical data such as surveys. " It is unclear how the clusters found in this model can be useful for the applications mentioned. The authors should discuss this more thoroughly.

Thank you for identifying this weakness in our explanation. We have strengthened the introduction in two ways. 1) We have made it clearer that the Axelrod model is a non-parametric opinion model easily adapted to ordinal data such as Likert-type scale responses and that this approach has important advantages over alternatives (e.g. averaging models). 2) We clarify that monocultural states are almost never seen in survey data (and such lack of variability is actively avoided when designing survey questions). For this reason the vanilla Axelrod model is not at all useful for modelling survey data, since as soon as the number of features (ie. survey items) exceeds the number of traits (ie. response options) homogeneity is guaranteed in a fully connected topology.

Specifically:

We have edited this sentence in the introduction, adding the highlighted text: “In this paper we demonstrate that an adapted version of Axelrod’s model of cultural dissemination [7] can be used to model opinion-based groups with data structures similar to survey data.”

We have edited the following sentence and added two following sentences, adding the highlighted text: “In principle, conceptualising Axelrod’s nominal cultural features and traits as ordinal attitudes will allow us to model the emergence of opinion-based groups with a data structure that maps cleanly on to raw survey data.” Note that opinion surveys typically use ordinal Likert-type response items (e.g. an item with several response options from Strongly Disagree to Strongly Agree). While these are frequently treated as interval data in analyses (ie. assuming consistent intervals between scale points and allowing arithmetic operations such as addition and subtraction), there is a strong argument that individual Likert-type items should properly be treated as ordinal, allowing only non-arithmetic operations. The original Axelrod model of cultural dissemination relies only on swapping, and our adaptions adds ranking, making it an excellent fit with Likert-type data.

We have changed the following sentence: “The clustering that emerges is useful for considering opinion-based groups in opinion dynamics models and empirical data such as surveys.”

Instead we argue:

"The resulting model is suited to natively modelling survey data, which frequently consists of Likert-type responses, since only ranking and swapping operations are required thus respecting the ordinal nature of the data. The model also avoids the homogoneous end-state which would always result when the original Axelrod model is used on survey-type data, as there are almost always features than traits (in other words, more items than response options).”

5. On line 192: "One outcome of this model is that extremists are less likely to change their position than moderates." This is not an outcome of the model, this is given by the specification of the model. If agents cannot copy the features which are not in the agreement threshold, features with extreme value traits cannot be modified unless the agent's neighbours features are also in the same extreme.

Reply: Indeed this is a specification rather than an outcome, and we have rephrased this sentence accordingly.

Specific remarks:

- The authors update the definition of the bipartite network according to the comment of reviewer 1, however, the definition still is not precisely correct.

Reply: Changed to “a graph with two types of nodes where edges must connect nodes of different types”

- What is the total number of agents, F, q in the simulations of figure 5?

Reply: F=6 and q=3, this is one of the two projections of the of figure 3 (this has been added to the caption).

Reply: Our model preserves those at the extremes whereas a model that allows both people move towards each other finds everyone ending up in the middle or the spectrum (See ref 36. Flache et al 2017 table 1). This prevalence of those on extremes is something that is observed in real systems (Brandt at al., 2015), we have added this reference now.

Brandt at al (2015). The Unthinking or Confident Extremist? Political Extremists Are More Likely Than Moderates to Reject Experimenter-Generated Anchors. Psychological Science, 26(2), 189–202).

Attachment

Submitted filename: response.pdf

Click here for additional data file.^{(53.1KB, pdf)}

PLoS One. doi: 10.1371/journal.pone.0233995.r005

Decision Letter 2

Carlos Gracia-Lázaro

18 May 2020

Agreement Threshold on Axelrod's model of Cultural Dissemination

PONE-D-19-31281R2

Dear Dr. Mac Carron,

We are pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it complies with all outstanding technical requirements.

Within one week, you will receive an e-mail containing information on the amendments required prior to publication. When all required modifications have been addressed, you will receive a formal acceptance letter and your manuscript will proceed to our production department and be scheduled for publication.

Shortly after the formal acceptance letter is sent, an invoice for payment will follow. To ensure an efficient production and billing process, please log into Editorial Manager at https://www.editorialmanager.com/pone/, click the "Update My Information" link at the top of the page, and update your user information. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to enable them to help maximize its impact. If they will be preparing press materials for this manuscript, you must inform our press team as soon as possible and no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

With kind regards,

Carlos Gracia-Lázaro

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

Reviewer #2: All comments have been addressed

Reviewer #3: All comments have been addressed

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #2: Yes

Reviewer #3: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #2: Yes

Reviewer #3: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #2: Yes

Reviewer #3: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #2: Yes

Reviewer #3: Yes

**********

6. Review Comments to the Author

Reviewer #2: All of my previous comments have been addressed and I believe this manuscript is ready for publication.

Reviewer #3: I believe the authors have addressed the comments concerning the justifications for their process of social influence and other specific remarks. I have to admit that I am still not convinced by the bipartite representation process, however, it is not the main contribution of the paper. The main contribution is the model and now it seems to be justified. Therefore, I would now recommend this manuscript for publication.

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #2: No

Reviewer #3: No

PLoS One. doi: 10.1371/journal.pone.0233995.r006

Acceptance letter

Carlos Gracia-Lázaro

22 May 2020

PONE-D-19-31281R2

Agreement Threshold on Axelrod's model of Cultural Dissemination

Dear Dr. MacCarron:

I am pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please notify them about your upcoming paper at this point, to enable them to help maximize its impact. If they will be preparing press materials for this manuscript, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

For any other questions or concerns, please email plosone@plos.org.

Thank you for submitting your work to PLOS ONE.

With kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Dr. Carlos Gracia-Lázaro

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Attachment

Submitted filename: PlosOne_review_2019.pdf

Click here for additional data file.^{(82.8KB, pdf)}

Attachment

Submitted filename: response.pdf

Click here for additional data file.^{(36.9KB, pdf)}

Attachment

Submitted filename: response.pdf

Click here for additional data file.^{(53.1KB, pdf)}

Data Availability Statement

The data is generated randomly using the model presented in the paper.

[pone.0233995.ref001] 1. Festinger L. A theory of social comparison processes. Human relations. 1954;7(2):117–140. 10.1177/001872675400700202 [DOI] [Google Scholar]

[pone.0233995.ref002] 2. Lewin K. Group discussion and social change. Basic Studies in Social Psychology New York: Holt, Rinehart and Winston. 1947;1965. [Google Scholar]

[pone.0233995.ref003] 3. Tajfel H, Turner JC, Austin WG, Worchel S. An integrative theory of intergroup conflict. Organizational identity: A reader. 1979; p. 56–65. [Google Scholar]

[pone.0233995.ref004] 4. Bar-Tal D. Group beliefs: A conception for analyzing group structure, processes, and behavior. Springer Science & Business Media; 2012. [Google Scholar]

[pone.0233995.ref005] 5. Kruglanski AW, Pierro A, Mannetti L, De Grada E. Groups as epistemic providers: need for closure and the unfolding of group-centrism. Psychological review. 2006;113(1):84. [DOI] [PubMed] [Google Scholar]

[pone.0233995.ref006] 6. Bliuc AM, McGarty C, Reynolds K, Muntele D. Opinion-based group membership as a predictor of commitment to political action. European Journal of Social Psychology. 2007;37(1):19–32. 10.1002/ejsp.334 [DOI] [Google Scholar]

[pone.0233995.ref007] 7. Axelrod R. The dissemination of culture: A model with local convergence and global polarization. Journal of conflict resolution. 1997;41(2):203–226. 10.1177/0022002797041002001 [DOI] [Google Scholar]

[pone.0233995.ref008] 8. Kero P, Lee D. Likert is Pronounced “LICK-urt” not “LIE-kurt” and the Data are Ordinal not Interval. Journal of applied measurement. 2016;17(4):502–509. [PubMed] [Google Scholar]

[pone.0233995.ref009] 9. Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Reviews of modern physics. 2009;81(2):591 10.1103/RevModPhys.81.591 [DOI] [Google Scholar]

[pone.0233995.ref010] 10. Boyd R, Richerson PJ. The origin and evolution of cultures. Oxford University Press; 2005. [Google Scholar]

[pone.0233995.ref011] 11. Valori L, Picciolo F, Allansdottir A, Garlaschelli D. Reconciling long-term cultural diversity and short-term collective social behavior. Proceedings of the National Academy of Sciences. 2012;109(4):1068–1073. 10.1073/pnas.1109514109 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233995.ref012] 12. Băbeanu AI, van de Vis J, Garlaschelli D. Ultrametricity increases the predictability of cultural dynamics. New Journal of Physics. 2018;20(10):103026 10.1088/1367-2630/aae566 [DOI] [Google Scholar]

[pone.0233995.ref013] 13. Băbeanu AI, Talman L, Garlaschelli D. Signs of universality in the structure of culture. The European Physical Journal B. 2017;90(12):237 10.1140/epjb/e2017-80337-7 [DOI] [Google Scholar]

[pone.0233995.ref014] 14. Stivala A, Robins G, Kashima Y, Kirley M. Ultrametric distribution of culture vectors in an extended Axelrod model of cultural dissemination. Scientific reports. 2014;4:4870. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233995.ref015] 15. Klemm K, Eguíluz VM, Toral R, San Miguel M. Global culture: A noise-induced transition in finite systems. Physical Review E. 2003;67(4):045101 10.1103/PhysRevE.67.045101 [DOI] [PubMed] [Google Scholar]

[pone.0233995.ref016] 16. Klemm K, Eguíluz VM, Toral R, San Miguel M. Nonequilibrium transitions in complex networks: A model of social interaction. Physical Review E. 2003;67(2):026120 10.1103/PhysRevE.67.026120 [DOI] [PubMed] [Google Scholar]

[pone.0233995.ref017] 17.Mazzitello KI, Candia J, Dossetti V. Effects of Mass Media and Cultural Drift in a Nonequilibrium Model for Social Influence; 2006. physics/0611189. Available from: http://cds.cern.ch/record/1000329.

[pone.0233995.ref018] 18. Battiston F, Nicosia V, Latora V, San Miguel M. Layered social influence promotes multiculturality in the Axelrod model. Scientific reports. 2017;7(1):1809 10.1038/s41598-017-02040-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233995.ref019] 19.Flache A, Macy MW. Why more contact may increase cultural polarization. arXiv preprint physics/0604196. 2006;.

[pone.0233995.ref020] 20. Deffuant G, Neau D, Amblard F, Weisbuch G. Mixing beliefs among interacting agents. Advances in Complex Systems. 2000;3(01n04):87–98. 10.1142/S0219525900000078 [DOI] [Google Scholar]

[pone.0233995.ref021] 21. Hegselmann R, Krause U, et al. Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of artificial societies and social simulation. 2002;5(3). [Google Scholar]

[pone.0233995.ref022] 22. Lord CG, Ross L, Lepper MR. Biased assimilation and attitude polarization: The effects of prior theories on subsequently considered evidence. Journal of personality and social psychology. 1979;37(11):2098 10.1037/0022-3514.37.11.2098 [DOI] [Google Scholar]

[pone.0233995.ref023] 23. Taber CS, Lodge M. Motivated skepticism in the evaluation of political beliefs. American journal of political science. 2006;50(3):755–769. 10.1111/j.1540-5907.2006.00214.x [DOI] [Google Scholar]

[pone.0233995.ref024] 24. De Sanctis L, Galla T. Effects of noise and confidence thresholds in nominal and metric Axelrod dynamics of social influence. Physical Review E. 2009;79(4):046108 10.1103/PhysRevE.79.046108 [DOI] [PubMed] [Google Scholar]

[pone.0233995.ref025] 25. Flache A, Macy MW. Local convergence and global diversity: From interpersonal to social influence. Journal of Conflict Resolution. 2011;55(6):970–995. 10.1177/0022002711414371 [DOI] [Google Scholar]

[pone.0233995.ref026] 26. Apolloni A, Gargiulo F. DIFFUSION PROCESSES THROUGH SOCIAL GROUPS’DYNAMICS. Advances in Complex Systems. 2011;14(02):151–167. 10.1142/S0219525911003037 [DOI] [Google Scholar]

[pone.0233995.ref027] 27.Martin S, Deffuant G, Nadal JP, Weisbuch G. Comparing the binary opinion vector version of the BC model with different approximating aggregated dynamics. M2M Workshop. 2004;.

[pone.0233995.ref028] 28. DeVellis RF. Scale development: theory and applications Applied social research methods series. Thousand Oaks: Sage Publications, Inc.; 2003. [Google Scholar]

[pone.0233995.ref029] 29. Sherif M, Hovland CI. Social judgment: Assimilation and contrast effects in communication and attitude change. Yale Univer. Press; 1961. [DOI] [PubMed] [Google Scholar]

[pone.0233995.ref030] 30. Pierro A, Mannetti L, Kruglanski AW, Sleeth-Keppler D. Relevance override: on the reduced impact of “cues” under high-motivation conditions of persuasion studies. Journal of Personality and Social Psychology. 2004;86(2):251. [DOI] [PubMed] [Google Scholar]

[pone.0233995.ref031] 31. Teigen KH. The language of uncertainty. Acta Psychologica. 1988;68(1):27–38. 10.1016/0001-6918(88)90043-1. [DOI] [Google Scholar]

[pone.0233995.ref032] 32.Flache A, Macy MW. What sustains cultural diversity and what undermines it? Axelrod and beyond. arXiv preprint physics/0604201. 2006;.

[pone.0233995.ref033] 33. Mäs M, Flache A. Differentiation without distancing. Explaining bi-polarization of opinions without negative influence. PloS one. 2013;8(11):e74516 10.1371/journal.pone.0074516 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233995.ref034] 34. Brandt MJ, Evans AM, Crawford JT. The unthinking or confident extremist? Political extremists are more likely than moderates to reject experimenter-generated anchors. Psychological Science. 2015;26(2):189–202. 10.1177/0956797614559730 [DOI] [PubMed] [Google Scholar]

[pone.0233995.ref035] 35. Flache A, Mäs M, Feliciani T, Chattoe-Brown E, Deffuant G, Huet S, et al. Models of Social Influence: Towards the Next Frontiers. Journal of Artificial Societies and Social Simulation. 2017;20(4):2 10.18564/jasss.3521 [DOI] [Google Scholar]

PERMALINK

Agreement threshold on Axelrod’s model of cultural dissemination

Pádraig MacCarron

Paul J Maher

Susan Fennell

Kevin Burke

James P Gleeson

Kevin Durrheim

Michael Quayle

Roles

Abstract

Introduction

Methods

Standard Axelrod model

Fig 1. An Axelrod simulation on a lattice with N = 100, F = 3 features and q = 5 traits paused after 40,000 time steps (i.e. not final state).

Fig 2. The bipartite representation of the Axelrod simulation in Fig 1 after 40,000 time-steps with F = 3 features (different colours) and q = 5 traits displaying which feature-trait combinations are selected.

Fig 4. The attitude-space from Fig 3.

Fig 5. The node-space projection (giant component) from Fig 3.

Agreement thresholds on the traits

Fig 3. The lattice and bipartite visualisation for the final state of Axelrod with the lowest agreement threshold on the traits for F = 6 and q = 3.

Projections

Number of clusters

Fig 6. The mean number of clusters per feature for q = 5 (left) and q = 7 (right) for different values of the agreement threshold a.

Fig 7. The probability density showing the distribution of the number of clusters for 1,000 simulations with q = 5 and varying the agreement threshold a.

Fig 8. The mean number of clusters per feature for q = 7 (left) and the probability density for the number of clusters for q = 7 and F = 4 (right) for a system with N = 1024.

Conclusion

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Carlos Gracia-Lázaro

Roles

Author response to Decision Letter 0

Decision Letter 1

Carlos Gracia-Lázaro

Roles

Author response to Decision Letter 1

Decision Letter 2

Carlos Gracia-Lázaro

Roles

Acceptance letter

Carlos Gracia-Lázaro

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases