Fig. 1. Concept of arbitrary elliptical birefringence.

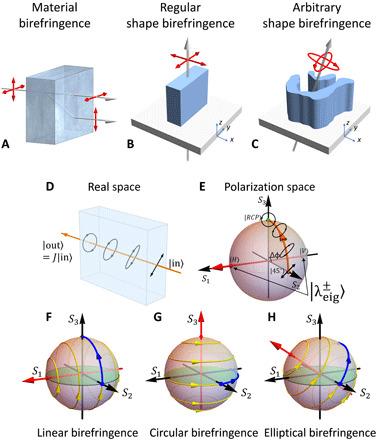
(A) Material birefringence results from intrinsic material anisotropy. (B) Regular shape birefringence considers simple symmetric structures at normal incidence. The red arrows represent the linearly polarized eigenstates. (C) Arbitrary shape birefringence uses freeform structures to unlock novel polarization functionalities. In this work, we demonstrate a device that can be continuously tuned from linear birefringence to elliptical birefringence by varying the angle of incidence. The red arrows represent the elliptical eigen-polarization states at oblique incidence. (D) The evolution of polarization state of a light beam propagating through a quarter–wave plate in the real space. (E) The same polarization evolution can be represented as a rotation (orange curve) in the polarization space (i.e., Poincaré sphere). (F to H) Polarization space representation of (F) linear, (G) circular, and (H) elliptical birefringence. In general, birefringence induces a rotation of polarization states on the Poincaré sphere (along the yellow lines), with the rotation axis (red axis) and rotation angle determined by the device’s eigen-polarization states (red dots) and retardance, respectively. The blue arrows show the trajectories for a quarter–wave retardance assuming a 45° linearly polarized incident light.