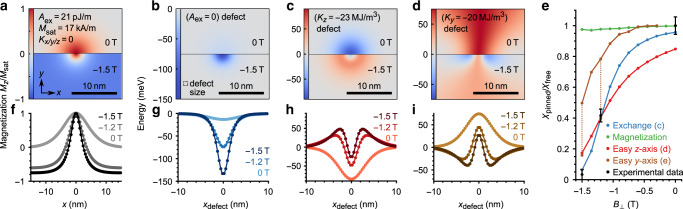
Fig. 3. Micromagnetic simulation of pinning potentials.
a Scaled, perpendicular magnetization mz = Mz/Msat of a simulated vortex core in a disk of height 10 nm and diameter 280 nm at B⊥ = 0 T (upper half) and B⊥ = −1.5 T (lower half) with magnetic parameters indicated. b–d Defect potentials for vortex core in meV at different types of magnetic defects, where only the marked parameters are changed with respect to a within a central area at the surface of 1.1 × 1.1 × 0.5 nm3 (3 × 3 × 1 cells). The display type is as in a. The spatial dependency of the vortex energy is simulated by scanning the defect through the vortex core (“Methods”). f–i Profile lines through the middle of a–d (from left to right) covering the 0 T and the −1.5 T area separately. An additional profile calculated for B⊥ = −1.2 T is added. e Simulated displacement rate ratio χpinned/χfree for the vortex core being trapped in the minima of the potentials shown in g–i. For the Aex defect, Aex = 0 is used and the defect size is adapted to fit the experimental data. For the Ky and Kz defects, we kept the defect size, while Ky and Kz are changed to fit the experimental data as good as possible. For the Ky defect, we show two values for the optimized Ky = 300 MJ/m3 and the full line with realistic Ky = 20 MJ/m3 connected by dotted lines to the optimized points. For the Msat defect, we use Msat = 0 within the same defect volume. The point for B⊥ = 0 T of the defect with easy y-axis is missing, since the purely repulsive potential did not enable a reliable determination of χpinned due to a strong dependence of vortex movement on starting conditions. Experimental data points are deduced from the average slope of the segments such as in Fig. 2f–h with statistical error bars.