Fig. 5. Computational challenging tasks profit from critical network dynamics (small Kext)—simple tasks do not.
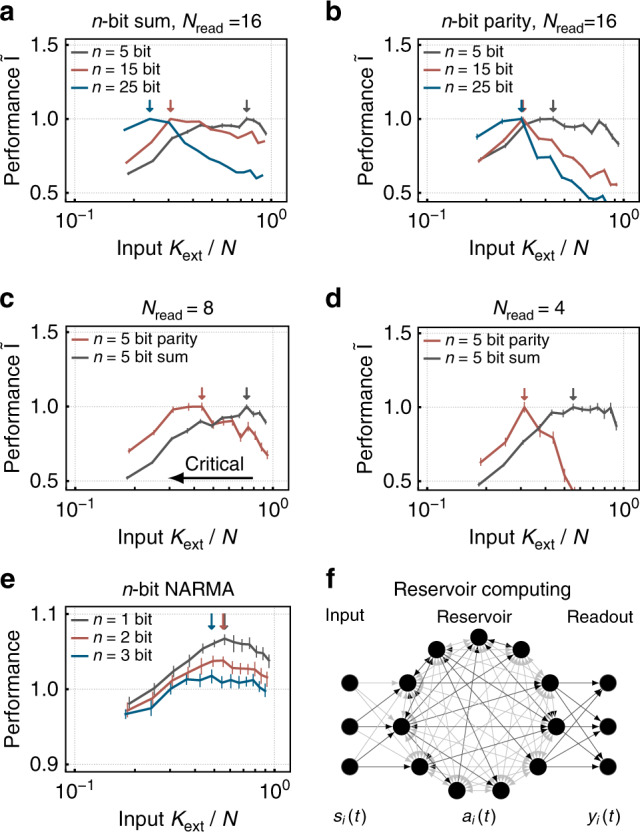
The network is used to solve (a) a n-bit sum and (b) a n-bit parity task by training a linear classifier on the activity of Nread = 16 neurons. Here, task complexity increases with n, the number of past inputs that need to be memorized and processed. For high n, task performance profits from criticality, whereas simple tasks suffer from criticality. Especially, the more complex, nonlinear parity tasks profits from criticality. Further, task complexity can be increased by restricting the classifier to c Nread = 8 and d Nread = 4. Again, the parity task increasingly profits from criticality with decreasing Nread. The performance is quantified by the normalized mutual information between the vote of the classifier and the parity or sum of the input. e Likewise, the peak performance moves toward criticality with increasing complexity in a NARMA task. The performance is quantified by the inverse NRMSE. Highest performance for a given task is highlighted by colored arrows. f Schematic reservoir computing setup.
