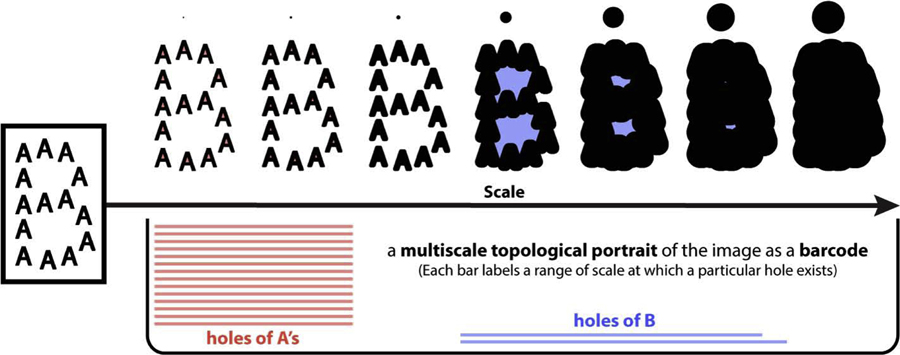
Fig 4. A big letter B made up of many small letter A’s and its multiscale topological portrait.

This figure illustrates intuitively how one may gain insights about a multiscale structure, i.e. a B of many A’s (image in left box), by studying the scale-dependency of its topological features, i.e. connected components and holes. The image may be viewed at succeeding greater scales as a sequence of images (above the scale axis) created by blowing up each pixel to a disk with increasing radius (size of disks are shown on top). At finer scales (left two images above the scale axis), the image has 14 connected components and 14 holes (from 14 A’s). At intermediate scales (4^th–6^th image from left above the scale axis), a large connected component is formed with two holes in it (from one B). At even larger scales, all holes are filled in (right-most image above the scale axis). A multiscale topological portrait (below the scale axis) summarizes the emergence and disappearance of holes as a function of scale. The portrait consists of a collection of bars (a barcode), where each bar represents a particular hole and the scales at which it exists. The portrait captures the separation between two descriptions (many A’s or a B) in scale, by capturing the scale-dependency and relative size of topological features (14 red bars appear only at finer scales and are shorter, reflecting A’s; blue bars only appear at grosser scales and are longer, reflecting the B; one blue bar is longer than the other because the lower loop in B is larger than the upper). This portrait is drawn by hand for illustrative purposes, a computed version based on persistent homology (see text) is shown in Fig S1 B.