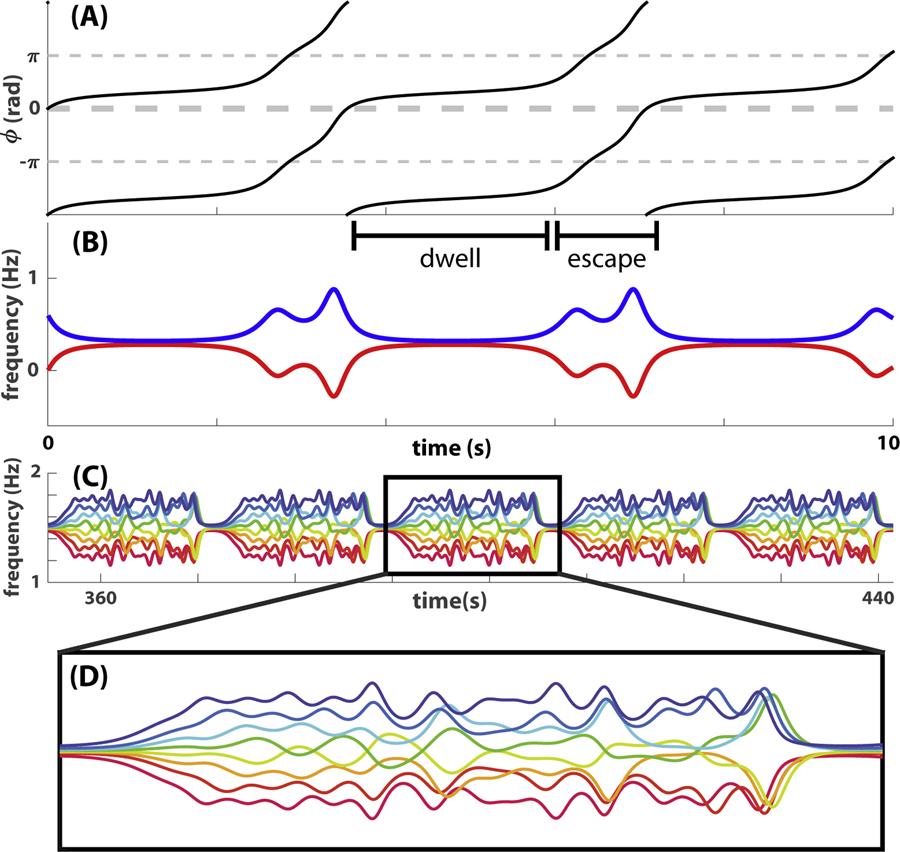
Fig 5. Metastable patterns characterized by topological features in frequency graphs.

Examples of simulated coordination dynamics are presented here to show why multiscale topological features are relevant to metastable patterns. (A-B) give a simple illustration of how relative phase dynamics (A) can be studied in terms of topological features in its corresponding frequency graph (B) defined as the collection of instantaneous frequency trajectories. A dwell in the relative phase (A; period labeled as “dwell”) is reflected as the merging of corresponding frequency trajectories into a single connected component (B, observed at a sufficiently gross scale). An escape in the relative phase (A; period labeled as “escape”) is reflected as the branching of frequency trajectories into two connected components or the formation of a loop if viewed in an extended time window (e.g. a window centered around the escape that extends to the middle of neighboring dwells). Thus, the dynamics of metastable phase coordination can be studied as topological features in the corresponding 2-dimensional frequency graph, which is very convenient when the dimension of the dynamical system increases. (C) shows the frequency graph of metastable coordination between eight oscillators, whereas a zoomed-in version of one period of the pattern is shown in (D). For such a complex pattern (D), the spacing between curves and the size of loops are very diverse, reflecting dwell-escape dynamics at various spatiotemporal scales. As a result, topological features in the frequency graph have to be measured at multiple scales to capture the complexity of such metastable patterns.