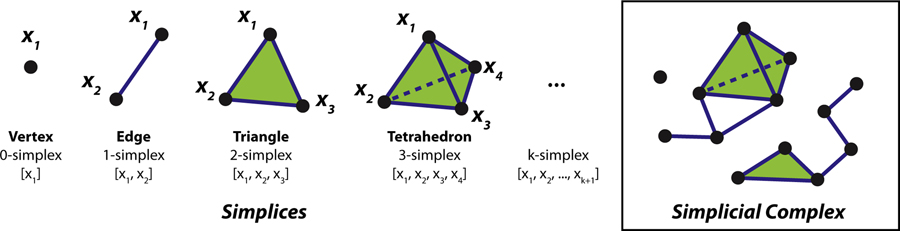
Fig 6. Simplices and a simplicial complex.
Simplices are elementary geometric objects of different dimensionality, which can be combined into more complex structures, i.e. simplicial complexes. A k-simplex can be thought of as a k-dimensional triangle, determined by its (k + 1) vertices; illustrations of such simplices are shown on the left. For example, a 2-simplex is a conventional triangle, determined by three vertices [x1, x2, x3]; a 0-simplex a vertex determined by itself [x1]; and a 1-simplex an edge determined by two vertices [x1, x2]. A simplicial complex (right box) is essentially a set of simplices, some of which are glued together along certain faces. Combinatorially, a simplicial complex can be described as a set of vertices plus a collection of its subsets which represent simplices connecting those vertices.