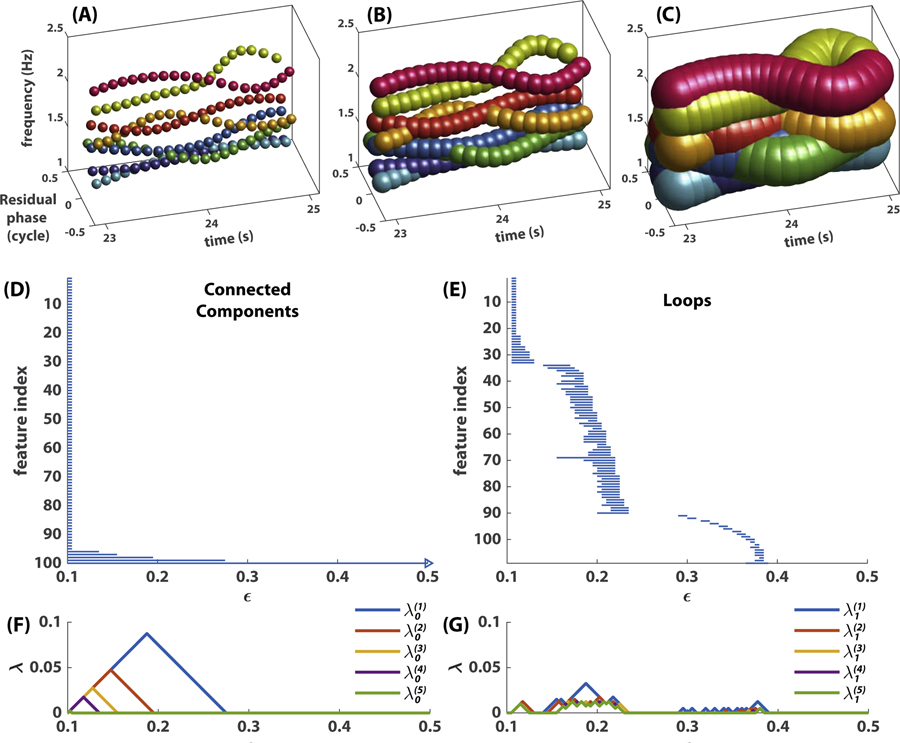
Fig 7. Persistence of topological features.

(A-C) shows a coordination pattern represented by point clouds at three different scales ϵ, i.e. a union of balls centered at each point with diameter ϵ = 0:1 in (A), ϵ = 0:2 in (B), or ϵ = 0:5 in (C). Note the merging of connected components from (A) to (B), the emergence of loops in (B) and their destruction in (C). The 0^th and 1^st persistent homology (connected components and loops respectively) of this point cloud are shown in (D,E) as barcodes, and in (F,G) as persistence landscapes. In (D,E), each horizontal bar represents a connected component (D) or loop (E), whose left (right) end indicates its birth (death) scale. Right arrow in (D) indicates that this component never dies (one connected component remains at any scale). (F,G) summarize the same information as a sequence of landscape functions, ${\lambda }_k^{\left(\mathcal{l}\right)}$, where k indicates that the landscape function is derived from the k^th persistent homology (i.e. 0^th persistent homology for connected components in F; 1^st persistent homology for loops in G) and ℓ indicates how prominent the landscape is (small ℓ more prominent; only the five most prominent landscape functions are shown).