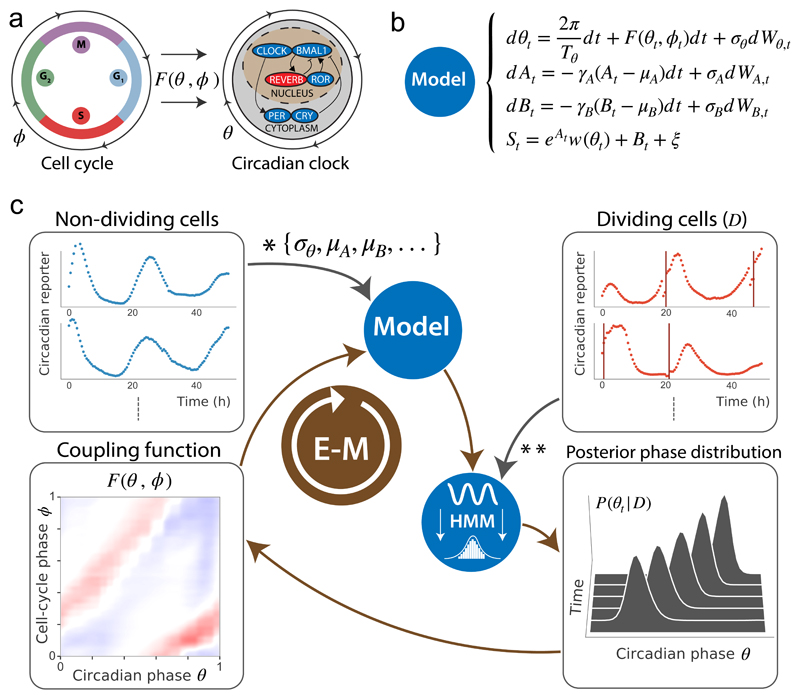
Figure 1. Reconstructing the phase dynamics and coupling of two biological oscillators.

(a) In mouse fibroblasts, the cell cycle (left) can influence the circadian oscillator (right) according to a coupling function F(θ, ϕ), where ϕ denotes the cell cycle and θ the circadian oscillator phases. (b) Stochastic model for the signal S_t using diffusion-drift SODEs for the circadian phase θ_t, amplitude A_t and background B_t fluctuations, as well as a function W(θ) linking the phase θ_t to the measured observations, and F(θ, ϕ) (c) Fluorescence microscopy traces (Rev-erbα-YFP circadian reporter) are recorded for non-dividing and dividing cells (top left and top right boxes). Coupling-independent parameters (*) are estimated from non-dividing cells while dividing cells are necessary to infer F(θ, ϕ) (**). The optimization problem is solved by converting the model to a HMM in which θ_t, A_t and B_t are latent variables. The HMM is used on traces to compute posterior probabilities of circadian phases (bottom right box), while the cell-cycle phase is retrieved using linear interpolation between successive divisions (top right box, vertical orange lines). An iterative EM algorithm then yields the converged F(θ, ϕ) (bottom left box).