Bayesian Inference: An Introduction to Hypothesis Testing Using Bayes Factors

Introduction

Monumental advances in computing power in recent decades have contributed to the rising popularity of Bayesian methods among applied researchers. This series of commentaries seeks to raise awareness among nicotine and tobacco researchers of Bayesian methods for analyzing experimental data. The current commentary introduces statistical inference via Bayes factors and demonstrates how they can be used to present evidence in favor of both alternative and null hypotheses.

Conceptualizing Hypothesis Testing via Bayes Factors

Bayesian inference is a fully probabilistic framework for drawing scientific conclusions that resembles how we naturally think about the world. Often, we hold an a priori position on a given issue. On a daily basis, we are confronted with facts about that issue. We regularly update our position in light of those facts. Bayesian inference follows this exact updating process. Formally stated, given a research question, at least one unknown parameter of interest, and some relevant data, Bayesian inference follows three basic steps. The process begins by specifying a prior probability distribution on the unknown parameter that often reflects accumulated knowledge about the research question. Next, the observed data, summarized using a likelihood function, are conditioned on the prior distribution. Finally, the resulting posterior distribution represents an updated state of knowledge about the unknown parameter and, by extension, the research question. Simulating data many times from the posterior distribution will ideally yield representative samples of the unknown parameter that we can interpret to answer the research question.

In an experimental context, we are often interested in evaluating two competing positions or hypotheses in light of data and making a determination about which to accept. In the context of Bayesian inference, hypothesis testing can be framed as a special case of model comparison where a model refers to a likelihood function and a prior distribution. Given two competing hypotheses and some relevant data, Bayesian hypothesis testing begins by specifying separate prior distributions to quantitatively describe each hypothesis. The combination of the likelihood function for the observed data with each of the prior distributions yields hypothesis-specific models. For each of the hypothesis-specific models, averaging (ie, integrating) the likelihood with respect to the prior distribution across the entire parameter space yields the probability of the data under the model and, therefore, the corresponding hypothesis. This quantity is more commonly referred to as the marginal likelihood and represents the average fit of the model to the data. The ratio of the marginal likelihoods for both hypothesis-specific models is known as the Bayes factor.

The Bayes factor is a central quantity of interest in Bayesian hypothesis testing. A Bayes factor has a range of near 0 to infinity and quantifies the extent to which data support one hypothesis over another. Bayes factors can be interpreted continuously so that a Bayes factor of 30 indicates that there is 30 times more support in the data for a given hypothesis than the alternative. They can also be interpreted discretely so that a Bayes factor of 3 or higher supports accepting a given hypothesis, 0.33 or lower supports accepting its alternative, and values in between are inconclusive.^1,2 Intuitively, the Bayes factor is the ratio of the odds of observing two competing hypotheses after examining relevant data compared to the odds of observing those hypotheses before examining the data. Therefore, the Bayes factor represents how we should update our knowledge about the hypotheses after examining data. We present two empirical examples with simulated data to demonstrate the computation and use of Bayes factors to test hypotheses.

Empirical Example 1: Is a Coin Fair or Tail-Biased?

Deciding whether a coin is fair or tail-biased is a simple, but useful example to illustrate hypothesis testing via Bayes factors. Let the null hypothesis be that the coin is fair, and let the alternative hypothesis be that the coin is tail-biased. We further intuit that coins, fair or not, can exhibit a considerable degree of variation in their head-tail biases depending on quality control issues during the minting process. Therefore, we use a Beta(5, 5) prior distribution to describe the null hypothesis. This distribution places the bulk of the probability density at or around 0.5 (ie, equal probability of heads or tails). Similarly, we use a Beta(3.8, 6.2) prior distribution to describe the alternative hypothesis. This skewed distribution places the bulk of the density at or around 0.35 (ie, lower probability of heads) and places less density on values greater than 0.4. The Beta prior is appropriate to describe hypotheses about a coin (and other binary variables) because it is continuously defined on the interval between 0 and 1 that the bias of a coin is also defined on; has hyperparameters that can be interpreted as the number of heads and tails; and provides flexibility in describing hypotheses because it does not have to be symmetric.

To test these hypotheses, we conduct a simple experiment by flipping the coin 20 times, recording 5 heads and 15 tails. We summarize this data using a Bernoulli(5, 15) likelihood function. After computing the marginal likelihoods of the models for both hypotheses, we find that the Bayes factor comparing the alternative hypothesis to the null is 2.65. This indicates that the data supports the alternative hypothesis that the coin is tail-biased over the null hypothesis that it is fair only by a factor of 2 or so. We further note that the Bayes factor falls into the range of inconclusive values. Therefore, we conclude that we need more experimental data to determine whether the coin is fair or tail-biased with greater certainty.

Empirical Example 2: Do Health Warnings for E-cigarettes Increase Worry About Health?

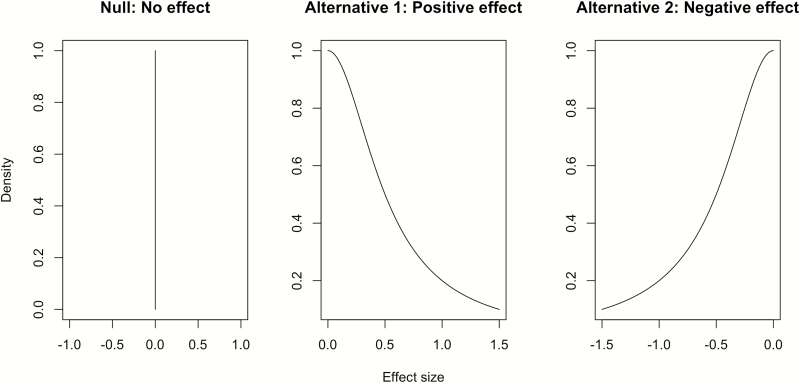
A more pertinent illustrative example of hypothesis testing via Bayes factors is deciding whether health warnings for e-cigarettes increase worry about one’s health. Let the null hypothesis be that health warnings have exactly no effect on worry. Let the first alternative hypothesis be one-sided that health warnings increase worry, and let the second alternative hypothesis also be one-sided that health warnings decrease worry. Bayes factors with the Jeffreys-Zellner-Siow (JZS) default prior can be used to evaluate these hypotheses.³ In comparison to other priors, default priors have mathematical properties that simplify the computation of Bayes factors. The JZS default prior describes hypotheses in terms of possible effect sizes (ie, Cohen’s d). As such, under the null hypothesis that health warnings have exactly no effect on worry, the prior distribution places the entire density on an effect size of 0 (Figure 1). Given that effect sizes in behavioral research in tobacco control are usually small,^4–6 the prior distributions for the alternative hypotheses use a scale parameter of 1/2 to distribute the density mostly over small positive or negative effect sizes.

Figure 1.

Prior distributions quantitatively describing competing hypotheses about the effect of e-cigarette health warnings on worry about one’s own health due to tobacco product use.

To test these hypotheses, we conduct a simple online experiment with 200 adults who vape every day or some days. The experiment randomizes participants to receive a stimulus depicting 1 of 5 e-cigarette devices (eg, vape pen) with or without a corresponding health warning. After viewing the stimulus for 10 seconds, participants complete a survey that includes an item on worry, “How worried are you about your health because of your e-cigarette use?”,⁷ with a response scale of 1 (“not at all”) to 5 (“extremely”). Participants who receive a health warning elicit mean worry of 2.38 (SD = 0.87), and those who do not elicit mean worry of 2.33 (SD = 0.84). The Bayes factors comparing the first and second alternative hypotheses to the null hypothesis are 0.16 and 0.30, respectively. These Bayes factors indicate that there is more support in the data for the null hypothesis than the alternative hypotheses. Taking the reciprocal of these Bayes factors indicates that there is approximately 3 to 6 times more support in the data for the null hypothesis that health warnings have no effect than either alternative. Therefore, we conclude that health warnings for e-cigarettes do not appear to affect worry based on the experimental data.

Conclusions

The hallmark of Bayesian model comparison (and other Bayesian approaches) is the incorporation of uncertainty at all stages of inference, particularly through the use of properly specified prior distributions. As a result, Bayesian model comparison has three practical advantages over conventional methods. First, Bayesian model comparison is not limited to tests of point null hypotheses.^8,9 In fact, the first empirical example essentially conceptualized the possibility of the coin being fair as an interval null hypothesis by permitting some unfair head-coin biases. Indeed, a great deal has already been written on how the use of point null hypotheses can lead to overstatements about the evidence for alternative hypotheses.¹⁰ Second, Bayesian model comparison is flexible enough to permit tests of any meaningful hypotheses.¹¹ As a result, the second empirical example demonstrated tests of two one-sided hypotheses against the same null hypothesis. Third, Bayesian model comparison uses the marginal likelihood, which is a measure of the average fit of a model across the parameter space.¹² Doing so leads to more accurate characterizations of the evidence for competing hypotheses because they account for uncertainty in parameter values even after observing the data instead of only focusing on the most likely values of those parameters.

Bayes factors specifically have three advantages over other inferential statistics. First, Bayes factors can provide direct evidence for the common null hypothesis of no difference.¹³ Second, they can reveal when experimental data is insensitive to the null and alternative hypotheses, clearly suggesting that the researcher should withhold judgment.¹³ Third, they can be interpreted continuously and thus provide an indication of the strength of the evidence for the null or alternative hypothesis. While Bayesian model comparison via Bayes factors leads to robust tests of competing hypotheses, this advantage is only realized when all hypotheses are quantitatively described using carefully chosen priors that are calibrated in light of accumulated knowledge. Furthermore, two analysts may choose different priors to describe the same hypothesis. This subjectivity in the choice of prior has promoted the development of a large class of Bayes factors for common analyses (eg, difference of means as illustrated in the second empirical example) that use default priors.^14–16 Thus, the analyst only needs to choose values for important parameters, as in the second empirical example, without having to select the functional form of the prior (eg, a Beta prior) as in the first empirical example. Published Bayesian analyses will often list priors and justify why they were chosen for full transparency (see Baig et al.¹⁷ for one succinct example). The next commentary will focus on informative hypotheses, prior specification when computing corresponding Bayes factors, and some Bayesian solutions for multiple testing. For the curious reader, the JASP package provides access to Bayes factors that use default priors for common analyses through a point-and-click interface similar to SPSS.¹⁸

Funding

This work was supported by the Office of The Director, National Institutes of Health (award number DP5OD023064).

Declaration of Interests

None declared.