Weight convergence analysis of DV-hop localization algorithm with GA

Abstract

The distance vector-hop (DV-hop) is a typical localization algorithm. It estimates sensor nodes location through detecting the hop count between nodes. To enhance the positional precision, the weight is used to estimate position, and the conventional wisdom is that the more hop counts are, the smaller value of weight will be. However, there has been no clear mathematical model among positioning error, hop count, and weight. This paper constructs a mathematical model between the weights and hops and analyzes the convergence of this model. Finally, the genetic algorithm is used to solve this mathematical weighted DV-hop (MW-GADV-hop) positioning model, the simulation results illustrate that the model construction is logical, and the positioning error of the model converges to 1/4R.

Introduction

In this unprecedented age of technology-driven modernization, technologies contribute greatly to the development of human society. For instance, fifth-generation wireless systems (5G) (Andrews et al. 2014; Boccardi et al. 2014) and the internet of things (IoT) (Gubbi et al. 2013; Al-Fuqaha et al. 2015) have greatly improved the speed of people’s communication and access to information and improved the user experience. In 2020, during the process of fighting the epidemic (COVID-19) (Zhou et al. 2020; Shi et al. 2020) worldwide, big data technology has played an irreplaceable role in the analysis of epidemic prevention and control. In these applications, location information plays an irreplaceable role.

Generally, satellite positioning is the main way to obtain location information. However, in areas where satellite signals are weak, such as tunnels and factory control systems, the positioning method based on wireless communication has become the main means of acquiring location. DV-hop (Niculescu and Nath 2003), as a prevailing and typical wireless communication-based localization algorithm, estimates sensor nodes location through detecting the hop count and acquiring estimated distance between nodes. However, this simple principle and operation cause the instability of the positional precision of the standard DV-hop algorithm. It makes the algorithm is unreliable in applications where accuracy is critical, such as medical health (Al Ameen et al. 2012). To reduce the error, scholars have proposed different improvement measures, including the introduction of weight models and optimization algorithms, and achieving a certain degree of accuracy improvement.

However, the conventional wisdom thinks that the weights will decrease with the hop counts increase. But there has been no clear mathematical model among positioning error, hop count, and weight. To address this issue, this paper improves the weight model and performs a convergence analysis. And the motivation and contribution are shown as follows: the goal of this study is to explore the convergence of the traditional weight model. Therefore, we construct a mathematical model between the weights and hops, reveal the relationship between the traditional weight model and the positioning error, and analyze and prove that the weight model is convergent. Through the proof of convergence, it provides a theoretical basis for scholars to improve the DV-hop positioning model. And this study uses the genetic algorithm (GA) (Goldberg 1989) to conduct a preliminary test of the model.

The remainder of this study is organized as follows. Section 2 provides a brief description of related work and introduces the traditional weight (TW) model with optimization algorithm; in Sect. 3, we construct a mathematical weight model (MW) based on the node communication features and analyze the convergence of this model. Section 4 uses the GA to solve this MW model and carries out the simulation test. Finally, the conclusions are drawn in Sect. 5.

Related work

Initially, the third phase of the DV-hop algorithm is to implement position calculation by a deterministic algorithm, such as the trilateration and the least square method. These methods require the algorithm provide an estimated distances with small error to achieve precise precision. But according to Eqs. (1) and (2), we can know this assumption that the acquisition of the highly accurate estimated distance is unrealistic for the DV-hop algorithm. Therefore, scholars use weight model and intelligent optimization algorithms to optimize the DV-hop algorithm to achieve a high accurate precision.

DV-hop with the optimization algorithms contains three stages. 1st phase: anchor nodes (ANs) transmit the packs to the network, other sensor nodes (contains the anchor and unknown nodes, UNs) receive the packs and retransmission them to network. During this process, each node counts the minimum number of hops required to communicate with other nodes. 2nd phase: according to the number of hops recorded, the distance per hop (dis_per) is calculated as follows:

$$\text{dis}\_{\text{per}}_i=\frac{{\sum }_{i\ne j}^{}∥{\text{AN}}_i-{\text{AN}}_j∥}{{\sum }_{i\ne j}^{}\text{hop}\_{\text{count}}_{i,j}}$$ 1

where ${\text{AN}}_i\text{and}{\text{AN}}_j$ denote the positions of the AN_i and AN_j, hop_count_i,j denotes the minimum hop count between AN_i and AN_j.

Then, the distance (dis_i,k) between AN_i and UN_k is estimated as follows:

$${\text{dis}}_{i,k}=\text{dis}\_{\text{per}}_i·\text{hop}\_{\text{count}}_{i,k}$$ 2

3rd phase: the optimization algorithm is used to solve the location of the UNs, and the model is as follows:

$$f_{i,k}=\sum _{i=1}^n\left|\sqrt{{\left(x_i-x_k\right)}^2+{\left(y_i-y_k\right)}^2}-{\text{dis}}_{i,k}\right|$$ 3

where (x_i, y_i) denotes the location of the AN_i, (x_k, y_k) denotes the location of the UN_i.

In 2007, Chuan (2008) proposed the concept of the weight and she thinks that the value of the weight is decrease with the hop count increase. In 2009, according to this viewpoint, Li et al. (2009) proposed a method for calculating the weight, which follows:

$${\text{Wh}}_j=\frac{1}{\text{hop}\_{\text{count}}_j}$$ 4

where the Wh_j denotes the hop-size weight of AN_j.

And the objective function model is calculated as follows:

$$f_{i,k}^{\ast }=\sum _{i=1}^n{\text{Wh}}_i^2{\left({\text{dis}}_{i,k}-\left|{\text{UN}}_i-{\text{AN}}_i\right|\right)}^2$$ 5

For the collinearity phenomenon of sensor nodes, Zhang et al. (2014) proposed to use the Voronoi diagram to divide the sensors network into difference multiple regions, each region containing an anchor node. Then, a weighted method is used to calculate the location of the UN. Gui et al. (2015) argued that when the hop count between the AN and UN is large, this AN will interfere rather than promote the positioning process of the UN. Therefore, he proposed to select three ANs closest to the UN for positioning, that is, select the three ANs with the smallest hop number for positioning. Song and Tam (2015) improved DV-hop with the weighted centroid, and the weight (W_i) is calculated as follows (where hop_i denotes the minimum hop count between the AN_i and UN). This model makes the closest AN has the greatest impact on the positioning results. Li et al. (2015) adapted a similar weight setting method to optimize the DV-hop algorithm.

$$w_i\frac{{\sum }_{i=1}^n{\text{hop}}_i}{n·{\text{hop}}_i}$$ 6

In recent years, with the recognition of this weight model, scholars have begun to seek to optimize it using various evolutionary algorithms; Mehrabi et al. (2017) proposed to optimize DV-hop with GA-PSO algorithm. Cui et al. (2017) developed a novel oriented cuckoo search (OCS) (Gandomi et al. 2013) algorithm to enhance the DV-hop performance. Sharma and Kumar (2018) also applied GA to the positioning process of wireless sensor nodes in three-dimensional (3D) space. Shi et al. (2019) proposed an improved DV-hop approach based on path matching and PSO. Cai et al. (2019a) introduced the rank transformation strategy to the bat algorithm (BA), proposed a fast triangle flip BA, and applied the algorithm to wireless sensor node localization. Further, scholars have also proposed new model improvements, such as the establishment of a multi-objective positioning model (Cai et al. 2019b; Wang et al. 2020; Kanwar and Kumar 2020) based on the theoretical hop distance.

However, it must be mentioned that although these algorithms improve the positional precision of the sensor nodes, they do not provide a convincing proof of the relationship among the errors, hop counts and weights. Therefore, based on the weighted conjectures put forward by scholars, this study constructs the corresponding model and analyzes the convergence of the model to reveal the potential relationship among the weights, hop counts, and errors.

Model establishment and analysis

The error models construction

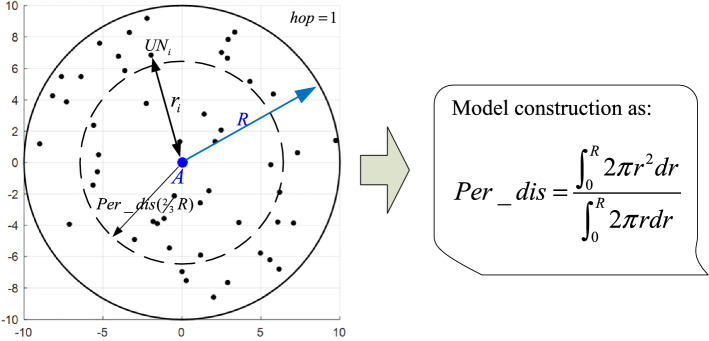
In the WSNs, according to the characteristics of the sensor node, we can get Fig. 1. In Fig. 1, the blue point denotes the anchor node, and the black points denote the UNs. Assumption all of the nodes is following the uniform distribution within the detecting area, and the maximum communication radius is R. The theoretical average distance per hop (Per_dis) when the hop count is one is calculated as follows in Eq. (7). Obviously, the calculation method of the Per_dis is different from the dis_per_i. The dis_per_i is obtained by the multi-hop transmission process; generally, the value of the dis_per_i is different from the dis_per_k. The Per_dis is obtained by probability statistics, and for different anchor nodes, the average distance is the same.

$$\text{Per}\_\text{dis}=\frac{{\int }_0^{R}2\pi r^2\text{d}r}{{\int }_0^{R}2\pi r\text{d}r}=\frac{2}{3}R$$ 7

Fig. 1.

Node distribution graph within the detection area when the hop count is 1

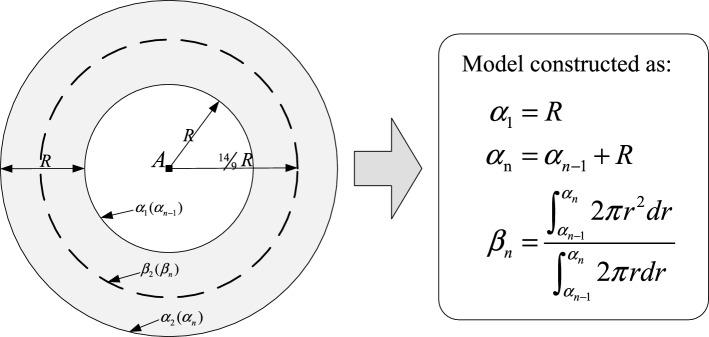
According to Eq. (7) and Fig. 1, we can obtain Fig. 2 when the hop count is two. Let the ${\alpha }_n$ indicate the maximum detectable range (also named the up bound) when the hop count is n, and the ${\alpha }_1$ is the R. Let the ${\beta }_n$ represent the average detection distance (also named the estimated distance) at the nth hop. In Fig. 2, the relationship between the ${\alpha }_n$ and ${\alpha }_{n-1}$ is shown in Eq. (8), because the communication radius is $R$, and the value of distance between the dotted line and the anchor node is $14/9R$, it is calculated by Eq. (9).

$${\alpha }_n={\alpha }_{n-1}+R=nR$$ 8

$${\beta }_n=\frac{{\int }_{{\alpha }_{n-1}}^{{\alpha }_n}2\pi r^2\text{d}r}{{\int }_{{\alpha }_{n-1}}^{{\alpha }_n}2\pi r\text{d}r}=\frac{2}{3}\left({\alpha }_n+{\alpha }_{n-1}\right)-\frac{2}{3}\frac{{\alpha }_n{\alpha }_{n-1}}{{\alpha }_n+{\alpha }_{n-1}}$$ 9

Fig. 2.

Node distribution graph within the detection area when the hop count is 2 (n)

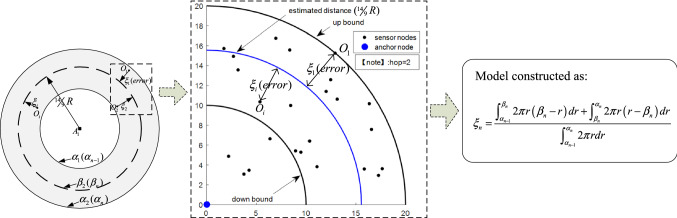
After obtaining the maximum detectable range and the average detection distance model, we also investigate the error model, as shown in Fig. 3, where the blue point denotes the anchor node, the black nodes denote the other sensor nodes, and the hop count is two. Let the ${\xi }_n$ represent the error when the hop count is n. As shown in Fig. 3, the error (${\xi }_2$) is that the distance between the sensor nodes (O_i) and the estimated distance (14/9R) within the detectable range when the hop count is two. Thus, the error model is expressed as Eq. (10).

$${\xi }_n=\frac{{\int }_{{\alpha }_{n-1}}^{{\beta }_n}2\pi r\left({\beta }_n-r\right)\text{d}r+{\int }_{{\beta }_n}^{{\alpha }_n}2\pi r\left(r-{\beta }_n\right)\text{d}r}{{\int }_{{\alpha }_{n-1}}^{{\alpha }_n}2\pi r\text{d}r}$$ 10

Fig. 3.

Error analysis with the detection area when the hop count is 2 (n)

Convergence analysis of the error model

In this subsection, we analyze the convergence of the error model. Firstly, when the hop count tends to infinity, Eq. (8) is follows:

$$\underset{n\to \infty }{lim}{\alpha }_n=\underset{n\to \infty }{lim}nR=\infty$$ 11

Similarly, Eq. (9) is calculated as follows:

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}{\beta }_n& =\underset{n\to \infty }{lim}\frac{2}{3}\left(nR+\left(n-1\right)R\right)-\frac{2}{3}\frac{nR\left(n-1\right)R}{nR+\left(n-1\right)R}\hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{\left(4nR-2R\right)\left(2nR-R\right)-2n^2{R}^2+2n{R}^2}{6nR-3R}\hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{8n^2{R}^2-4n{R}^2-4n{R}^2+2R^2-2n^2{R}^2+2n{R}^2}{6nR-3R}\hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{6n^2{R}^2-6n{R}^2+2R^2}{6nR-3R}\hfill \\ \hfill & =\infty \hfill \\ \hfill \end{array}$$ 12

Then, when the hop count tends to infinity, the error model can be indicated as follows:

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}{\xi }_n& =\underset{n\to \infty }{lim}\frac{{\int }_{{\alpha }_{n-1}}^{{\beta }_n}2\pi r\left({\beta }_n-r\right)\text{d}r+{\int }_{{\beta }_n}^{{\alpha }_n}2\pi r\left(r-{\beta }_n\right)\text{d}r}{{\int }_{{\alpha }_{n-1}}^{{\alpha }_n}2\pi r\text{d}r}\hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{\frac{2}{3}{\beta }_n^3-{\beta }_n\left({\alpha }_{n-1}^2+{\alpha }_n^2\right)+\frac{2}{3}\left({\alpha }_{n-1}^3+{\alpha }_n^3\right)}{{\alpha }_n^2-{\alpha }_{n-1}^2}\hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{\frac{2}{3}\left({\alpha }_n-\frac{1}{2}{R}^3\right)-\left({\alpha }_n-\frac{1}{2}R\right)\left({\alpha }_{n-1}^2+{\alpha }_n^2\right)+\frac{2}{3}\left({\alpha }_{n-1}^3+{\alpha }_n^3\right)}{{\alpha }_n^2-{\left({\alpha }_n-R\right)}^2}\hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{\frac{2}{3}\left({\alpha }_n^3-3{\alpha }_n^2\frac{1}{2}R+3{\alpha }_n\frac{1}{4}{R}^2-\frac{1}{8}R\right)-\left({\alpha }_n-\frac{1}{2}R\right)\left({\left({\alpha }_n-R\right)}^2+{\alpha }_n^2\right)+\frac{2}{3}\left({\left({\alpha }_n-R\right)}^3+{\alpha }_n^3\right)}{2{\alpha }_{n}R-R^2}\hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{\frac{2}{3}{\alpha }_n^3-{\alpha }_n^{2}R+\frac{1}{2}{\alpha }_n{R}^2-\frac{1}{12}{R}^3-\left({\alpha }_n-\frac{1}{2}R\right)\left({\alpha }_n^2-2{\alpha }_{n}R+R^2+{\alpha }_n^2\right)+\frac{2}{3}\left(2{\alpha }_n^3-3{\alpha }_n^{2}R+3{\alpha }_n{R}^2-R^3\right)}{2{\alpha }_{n}R-R^2}\hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{2{\alpha }_n^3-3{\alpha }_n^{2}R+\frac{1}{2}{\alpha }_n{R}^2+2{\alpha }_n{R}^2-\frac{3}{4}{R}^3-\left(2{\alpha }_n^3-2{\alpha }_n^{2}R+{\alpha }_n{R}^2-{\alpha }_n{R}^2-\frac{1}{2}{R}^3\right)}{2{\alpha }_{n}R-R^2}\hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{\frac{1}{2}{\alpha }_n{R}^2-\frac{1}{4}{R}^3}{2{\alpha }_{n}R-R^2}\hfill \\ \hfill & =\frac{1}{4}R\hfill \\ \hfill \end{array}$$ 13

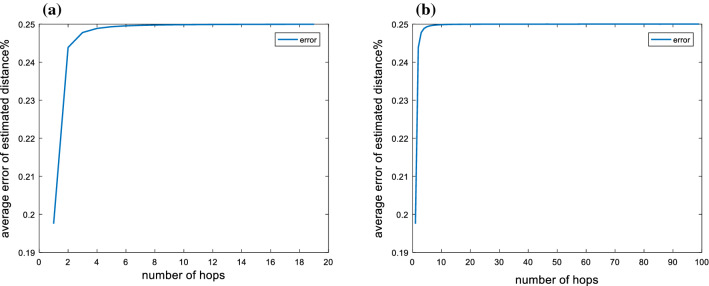
Thus, we can obtain that when the hop count tends to infinity (where, the sensor nodes are following the uniform distribution and the number of sensor nodes tends to infinity), the error of estimated distance converges to 1/4R. To reveal the convergence trend of the error, we calculated the error of this model with different hop counts, and the results are shown in Fig. 4. Obviously, the error increases as the number of hops increases and eventually converges to 1/4R.

Fig. 4.

Error analysis with the detection area when the hop count is 2 (n). a The total hop count is 20, and b the total hop count is 100

Construction and solution of weight model

The traditional weight model considers that the smaller the hop count, the stronger the influence on unknown nodes. However, this viewpoint ignores the relationship between the weight and the errors, because the convergence is not analyzed. Based on this deficiency, this study constructs the mathematical model based on the weight and errors, and the convergence of the error is analyzed in the subsection 3.2. And the weight model is expressed as follows:

$${\delta }_i=\frac{1}{{\xi }_i},i=1,2,\dots ,n$$ 14

where $n$ denotes the total number of ANs,${\delta }_i$ denotes the weight model, and it means the larger the theoretical error, the smaller the value of the weight.

Then, the weight model is normalized, as shown in Eq. (15).

$${\omega }_i=\frac{{\delta }_i}{{\sum }_{i=1}^n{\delta }_i}$$ 15

Thus, the objective of localization is expressed as:

$${\text{fitness}}_{i,k}=\sum _{i=1}^n{\omega }_i({\text{dis}}_{i,k}-|{\text{UN}}_i-{\text{AN}}_i{|)}^2$$ 16

Inspired by the traditional weight model, a weight model based on error variation was established and proved to be convergent. And this study solves this mathematical weighted DV-hop with genetic algorithm, named the MW-GADV-hop. The implementation of MW-GADV-hop is shown in Algorithm 1.

Simulation results

Simulation environment and evaluation criteria

To test the performance of the proposed weight model, experimental simulations were conducted in MATLAB 2016a. Then, we analyzed the performance of the algorithm and compared it with the DV-hop, TW-GADV-hop (Sharma and Kumar 2018), TW-PSODV-hop (Shi et al. 2019), and FTF-BADV-hop (Cai et al. 2019a). And the parameters are listed in Table 1.

Table 1.

Parameter settings

Parameters	Value
DV-hop
Network type	C-, O- and X-shaped network
Detection area	100 m × 100 m
Nodes (n)	100 (50–100)
Beacon nodes (n)	20 (5–30)
R (m)	25 (15–40)
GA
Population	20
Variable dimension (v)	2*(N − n)
Cross probability	0.9
Mutation probability	1/v
Maximum generation	500
Independently runtime	30

To evaluate the performance proposed algorithms, this study uses the average localization error (ALE) as the evaluation criteria, as follows:

$$\text{ALE}=\frac{100}{(N-n)·R}\sum _{i=1}^{N-n}\sqrt{{(x_i^{\ast }-x_i)}^2+{(y_i^{\ast }-y_i)}^2}$$ 17

where $(x_i^{\ast },y_i^{\ast })$ denotes the estimated location of the ${\text{UN}}_i$, $(x_i,y_i)$ denotes the actual location of the ${\text{UN}}_i$.

The main purpose of this study is to construct a mathematical model of weight based on the traditional weight concept and to prove the convergence of the model, instead of creating a new weight model. Therefore, our weight model should theoretically have similar positioning performance to the traditional weight model. In order to test the positioning performance, we execute the algorithm within the different network topologies, as shown in Fig. 5, where the ‘.’ denotes the UNs and the ‘*’ denotes the ANs. Obviously, the network topology contains the C- shaped, O-shaped and X-shaped networks.

Fig. 5.

Three complex shape test networks. a The C-shaped, b the O-shaped, and c the X-shaped

Different radii test

Table 2 and Fig. 6 show the simulation results with the different radii. From the distribution of the smallest error in Table 2, the MW-GADV-hop proposed in this paper does not show outstanding positioning advantages. And it has similar performance to other DV-hop algorithms solved by optimization algorithms (FTF-BADV-hop, TW-PSODV-hop, and TW-GADV-hop) in different network topologies. Obviously, in Fig. 6, DV-hop always maintains the maximum positioning error with different radii. And in C-shaped and X-shaped networks, MW-GADV-hop is significantly better than TW-GADV-hop solved by the same genetic algorithm.

Table 2.

The results with different radii test

Radii	15	20	25	30	35	40
C-shaped network
DV-hop	172.33	112.53	63.73	49.78	44.81	41.62
FTF-BADV-hop	94.01	63.49	36.58	31.15	29.89	27.32
TW-PSODV-hop	93.76	63.01	36.30	31.20	29.51	27.56
TW-GADV-hop	50.99	39.28	31.32	31.17	30.96	31.64
MW-GADV-hop	69.10	51.71	34.33	30.12	30.49	30.39
O-shaped network
DV-hop	117.88	56.50	44.77	39.39	29.24	31.28
FTF-BADV-hop	49.49	27.03	24.06	25.27	18.11	20.37
TW-PSODV-hop	50.58	27.28	24.33	24.74	18.06	20.58
TW-GADV-hop	44.14	31.77	28.15	30.39	25.70	28.37
MW-GADV-hop	49.20	27.55	23.96	25.15	19.86	22.11
X-shaped network
DV-hop	80.18	54.22	43.49	39.39	37.15	36.29
FTF-BADV-hop	43.96	32.29	34.45	35.32	28.44	27.68
TW-PSODV-hop	45.06	32.52	34.23	34.42	28.43	27.41
TW-GADV-hop	41.57	36.93	38.60	37.58	35.50	34.59
MW-GADV-hop	44.36	33.34	32.08	31.25	29.90	29.95

Bold values indicate the minimum error (the best solution)

Fig. 6.

The results with different radii test. a The results of C-shaped network, b the results of O-shaped network, and c the results of X-shaped network

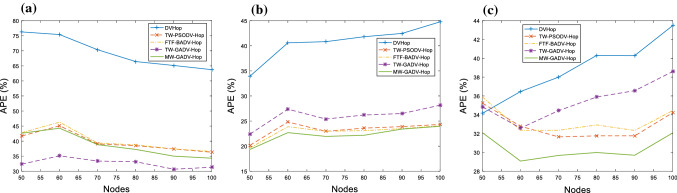
Different nodes test

Table 3 and Fig. 7 show the simulation results with the different numbers of nodes. From Table 3, MW-GADV-hop always maintains the minimum positioning error in O-shaped and X-shaped networks. And compared with DV-hop algorithm, the errors of MW-GADV-hop dropped by 33.64%, 20.81%, and 11.41%, respectively. From Fig. 7, in C-shaped network, the positioning performance of MW-GADV-hop is inferior to TW-GADV-hop, but similar to the FTF-BADV-hop and TW-PSODV-hop.

Table 3.

The results with different nodes test

Number of nodes	50	60	70	80	90	100
C-shaped network
DV-hop	76.27	75.39	70.34	66.42	65.12	63.73
FTF-BADV-hop	42.82	46.29	39.38	38.75	37.42	36.57
TW-PSODV-hop	41.70	45.09	39.05	38.47	37.40	36.30
TW-GADV-hop	32.35	35.11	33.38	33.15	30.68	31.32
MW-GADV-hop	42.63	44.29	38.83	37.24	35.01	34.33
O-shaped network
DV-hop	33.92	40.59	40.82	41.80	42.46	44.77
FTF-BADV-hop	19.64	23.87	22.97	23.09	23.49	24.06
TW-PSODV-hop	20.15	24.81	22.96	23.59	23.89	24.33
TW-GADV-hop	22.38	27.36	25.40	26.20	26.50	28.15
MW-GADV-hop	19.34	22.69	21.94	22.17	23.40	23.96
X-shaped network
DV-hop	34.16	36.47	38.00	40.31	40.30	43.49
FTF-BADV-hop	35.89	32.35	32.35	32.92	32.33	34.45
TW-PSODV-hop	35.24	32.78	31.65	31.76	31.76	34.23
TW-GADV-hop	34.85	32.58	34.44	35.89	36.56	38.60
MW-GADV-hop	32.10	29.08	29.68	29.99	29.70	32.08

Bold values indicate the minimum error (the best solution)

Fig. 7.

The results with different nodes test. a The C-shaped network, b the O-shaped network, and c the X-shaped network

Different anchor nodes test

Table 4 and Fig. 8 show the simulation results with the different numbers of ANs. From Table 4, the performance of MW-GADV-hop is slightly inferior to TW-GADV-hop in C-shaped network and superior to FTF-BADV-hop, TW-PSODV-hop, and TW-GADV-hop in other networks. From Fig. 8, compared with other algorithms, MW-GADV-hop has less volatility, which indicates it is not sensitive to the number of anchor nodes, reflecting the strong robustness of the MW-GADV-hop.

Table 4.

The results with different ANs test

Number of ANs	5	10	15	20	25	30
C-shaped network
DV-hop	88.45	67.42	69.45	63.73	64.88	69.80
FTF-BADV-hop	49.83	42.62	48.62	36.57	53.21	54.83
TW-PSODV-hop	46.99	41.45	46.81	36.30	52.46	52.71
TW-GADV-hop	116.76	43.28	37.54	31.32	33.21	31.30
MW-GADV-hop	116.80	41.40	42.59	34.33	38.62	36.87
O-shaped network
DV-hop	98.08	79.95	38.47	44.77	38.28	40.49
FTF-BADV-hop	31.75	34.34	28.02	24.06	32.24	30.97
TW-PSODV-hop	30.75	33.09	28.90	24.33	32.71	31.72
TW-GADV-hop	76.28	51.68	30.23	28.15	26.26	25.00
MW-GADV-hop	63.65	47.06	25.42	23.96	23.09	21.76
X-shaped network
DV-hop	58.46	59.14	47.89	43.49	46.66	48.57
FTF-BADV-hop	42.81	39.93	42.34	34.45	46.13	45.54
TW-PSODV-hop	41.99	39.80	41.92	34.23	47.04	46.36
TW-GADV-hop	60.86	42.36	38.83	38.60	36.91	33.12
MW-GADV-hop	51.73	36.52	32.82	32.08	32.06	27.80

Bold values indicate the minimum error (the best solution)

Fig. 8.

The results with different ANs test. a The results of C-shaped network, b the results of O-shaped network, and c the results of X-shaped network

Time complexity

Table 5 shows the time complexity of these algorithms, where the MaxG denotes the maximum generation and NP indicates the number of population in the algorithms. From Table 5, it can observe that the time complexity of the TW-GADV-hop and MW-GADV-hop is similar, and they are superior to the time complexity of the FTF-BADV-hop and TW-PSODV-hop. Therefore, our algorithm has higher timeliness than other algorithms during the location process.

Table 5.

Time complexity

Algorithms	Time complexity
FTF-BADV-hop	$O(\text{Max}G·(N-n)·NP·logNP)$
TW-PSODV-hop	$O(\text{Max}G·(N-n)·NP·logNP)$
TW-GADV-hop	$O(\text{Max}G·NP·logNP)$
MW-GADV-hop	$O(\text{Max}G·NP·logNP)$

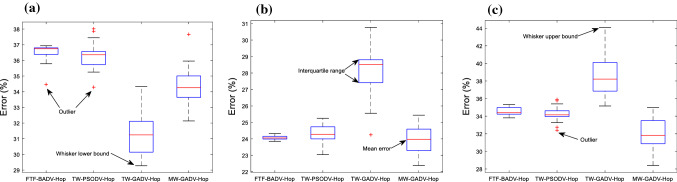
Figure 9 shows boxplot analysis of the results, and this figure exhibits the distribution of the simulation results. And the ‘mean error’ denotes the mean of the results of thirty runs, and the ‘Whisker lower bound’ and ‘Whisker up bound,’ respectively, denote the minimum and maximum error. From Fig. 9, FTF-BADV-hop has the smallest error interval; however, although the error interval of MW-GADV-hop is larger than FTF-BADV-hop, the error distribution interval is lower, which means MW-GADV-hop has higher reliability. In C-shaped network, MW-GADV-hop is inferior to TW-GADV-hop.

Fig. 9.

The boxplot analysis of the results. a The results of C-shaped network, b the results of O-shaped network, and c the results of X-shaped network

Conclusions

In this study, to explore the convergence of traditional weight models, we analyze the communication principle of sensor nodes. According to the traditional weight models, this study constructs a mathematical weight model based on the node communication features. Then, we analyze the convergence of the model and prove that when the number of hop count tends to infinity, the error of the model converges to 1/4R (where the sensor nodes are following the uniform distribution in the detection region and needs to have enough nodes). Finally, to test the model performance of this model, this algorithm is widely tested on different complex networks. The simulation results illustrate that the performance of this model is similar to other algorithms on the C-shaped network, and it is superior to other algorithms on the O-shaped and X-shaped networks.

Although the model achieved better positioning performance and proved to be convergent, we notice that some results do not converge to 1/4R. Therefore, we will explore a more reasonable and generalized weight model based on the communication principle of nodes to achieve better positioning performance.

Compliance with ethical standards

Conflict of interest

The author declares that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants performed by any of the authors.

Informed consent

Informed consent was obtained from all individual participants included in the study.