Global dynamics of a fractional order model for the transmission of HIV epidemic with optimal control

Highlights

• •Fractional order SEIR epidemic model with two infectious 'stages' is proposed.
• •Global dynamics of the model is performed.
• •Numerical simulations using Adam-Beshforth-Moulton method are conducted to support our results.
• •To present fractional order derivative as tool for the description of memory effects.
• •Fractional optimality condition for the proposed model is formulated.
• •Euler-Lagrange necessary conditions for the optimality of fractional optimal controls are obtained.

Abstract

In this paper, a nonlinear fractional order epidemic model for HIV transmission is proposed and analyzed by including extra compartment namely exposed class to the basic SIR epidemic model. Also, the infected class of female sex workers is divided into unaware infectives and the aware infectives. The focus is on the spread of HIV by female sex workers through prostitution, because in the present world sexual transmission is the major cause of the HIV transmission. The exposed class contains those susceptible males in the population who have sexual contact with the female sex workers and are exposed to the infection directly or indirectly. The Caputo type fractional derivative is involved and generalized Adams-Bashforth-Moulton method is employed to numerically solve the proposed model. Model equilibria are determined and their stability analysis is considered by using fractional Routh-Hurwitz stability criterion and fractional La-Salle invariant principle. Analysis of the model demonstrates that the population is free from the disease if ${\mathcal{R}}_0<1$ and disease spreads in the population if ${\mathcal{R}}_0>1$. Meanwhile, by using Lyapunov functional approach, the global dynamics of the endemic equilibrium point is discussed. Furthermore, for the fractional optimal control problem associated with the control strategies such as condom use for exposed class, treatment for aware infectives, awareness about disease among unaware infectives and behavioral change for susceptibles, we formulated a fractional optimality condition for the proposed model. The existence of fractional optimal control is analyzed and the Euler-Lagrange necessary conditions for the optimality of fractional optimal control are obtained. The effectiveness of control strategies is shown through numerical simulations and it can be seen through simulation, that the control measures effectively increase the quality of life and age limit of the HIV patients. It significantly reduces the number of HIV/AIDS patients during the whole epidemic.

1. Introduction

Epidemiology mainly deals with the infectious diseases and predicts their occurrence, transmission as well as control in a population. It identifies the factors responsible for disease spread, facilitates treatment quality and health services, provides necessary measures for prevention, treatment, planning in order to improve the efficiency and effectiveness of health services [1]. HIV is a retrovirus which is discovered in 1981 in USA among the gay community causes an AIDS a severe life intimidating ailment. At present, there is no vaccine or cure for AIDS, that makes it an incurable disease with high mortality rate (there are almost 25 million deaths by AIDS per year worldwide), also it spread quickly affecting about 14,000 new case/day. The time duration for HIV to develop AIDS mostly lasts from 6 months to 15 year. The virus destructs CD4⁺ T-cells ending of loss of cell mediated immunity, thus makes the immune system susceptible to cancers and various infectious diseases. The routes of transmission of HIV virus are unprotected sexual intercourse, through blood by sharing contaminated needles or infected blood transfusion, from mother to her child during pregnancy i.e., vertical transmission [2].

Mathematical models act as a tool which the researchers have extensively used in the epidemiology of HIV/AIDS to get the understanding of the major contributing factors in a given epidemic. Zafar et al. [3] fractionally studied the HIV/AIDS epidemics with three solution approaches namely Adams-Bashforth Moulton method, Grunwald Letnikov approach and Grunwald Letnikov approach with binomial coefficients. In their study, they have analyzed the model and obtained the necessary conditions for the existence and stability of both the equilibria. They have shown that the system is stable if ${\mathcal{R}}_0<1$ and if ${\mathcal{R}}_0>1$, then system becomes unstable and endemic equilibrium exists which behaves as an attractor. Wang et al. [4] studied a delayed fractional order SIR model with saturated incidence and treatment functions. They have provided the sufficient conditions that guarantee the existence of equilibria and discussed the global stability results for both disease-free equilibrium as well as endemic equilibrium by constructing a suitable Lyapunov functions. Almeida [5] in his paper studied a fractional SEIR epidemic model in presence of treatment. He analysed the model and his main focus was on the fractional differential equations in order to describe the dynamics of certain epidemics. Further, he proved the local stability for both equilibria. Carvalho et al. [6] provided a HIV/HCV coinfection fractional order model to understand the impact of HIV viral load on the coinfection. Their main motive in the model was to provide good fits to real data from patients suffering from several diseases such as HIV, HCV, dengue fever and many more. They have numerically suggested that the HIV viral load impacts impressively the severity of the HCV infection. Also, by their results they showed that the treatment efficacy is also influential over the natural progression of HCV on the HIV/HCV coinfection. Recently, Kheiri and Jafari [7] analysed a multi-patch HIV/AIDS epidemic model with fractional order derivatives and investigated the effect of human movement on the spread of HIV/AIDS epidemic among patches. They derived the basic reproduction number ${\mathcal{R}}_0$ of the model and studied the local as well as global stability of the equilibria on the basis of ${\mathcal{R}}_0$ . They have shown that the system is stable if ${\mathcal{R}}_0<1$ and it becomes unstable if ${\mathcal{R}}_0>1$. They also obtained the sufficient conditions under which the endemic equilibrium is unique and globally asymptotically stable. Besides this, they formulated a fractional optimal control problem in which the state and co-state equations are given in term of the left fractional derivatives. They incorporated in the model time dependent controls in order to control the spread of HIV/AIDS epidemics. They also derived the necessary conditions for the fractional optimal control in their proposed model. The effect of varying the fractional order on the disease spread is also studied in their model. Researchers have continuously studied the fractional order models of HIV disease dynamics and provided many well-known mathematical techniques for the solution of these models for the dynamics of HIV epidemics [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19]. Besides this, a number of studies on fractional order modeling of other infectious diseases can be found in the literature [20], [21], [22], [23]. The fractional order derivative not only find its application on modeling infectious diseases but in other fields as well like vibration equation [24] and so on.

The optimal control theory is developing fast and its various applications are extensively used in many fields of science and engineering [25]. This theory for linear systems has been highly improved [26], however, the nonlinear optimal control problem (OCP) has become a strong topic and should be deeper investigated [27], [28]. Jajarmi and Baleanu [29] proposed a new approach based on the modal series method and eigenvalue decomposition technique to solve a class of nonlinear optimal control problems. They have also investigated the convergence analysis of their suggested technique. Jajarmi et al. [30] proposed a new approach for the optimal control of time-varying delay systems with external persistent matched disturbances. In their internal model principle, they converted original time-delay model with disturbance into an augmented system without any disturbance. Then, they selected a quadratic performance index for the augmented system to form an undisturbed time-delay optimal control problem. The necessary optimality conditions are then derived in terms of a two-point boundary value problem involving advance and delay arguments. At the end they finally provided a fast iterative algorithm for the latter advance-delay boundary value problem. They also investigated the convergence of the new iterative technique.

The purpose of dealing with fractional order systems is the memory and hereditary properties which are the complex behavioral patterns of biological systems gives us more realistic way to model HIV/AIDS systems. In the fractional order models, the memory property allows the integration of more information from the past which predicts and translates the models more accurately. Also, the hereditary property describes the genetic profile along with age and status of the immune system. Because of such properties fractional order calculus have found wide applications to model dynamics processes in many well-known fields of science, engineering, biology, medicine and many other [31], [32]. Saeedian et al. [33] formulated SIR epidemic model with the inclusion of memory effect and studied its behavior along the memory effect on the disease spread with the help of fractional derivatives. Rihan [34] provided a class of fractional order differential models of biological systems with memory, such as dynamics of tumor-immune system and dynamics of HIV infection of CD4⁺ T cells.

Communicable diseases have been a cause of global concern throughout the history of mankind. Its outbreak severely affects the morbidity and the mortality rates across the globe. It is therefore important to implement the control measures to prevent and control the disease spread among the populations. Kheiri and Jafari [35] formulated a fractional optimal control epidemic model of HIV/AIDS with random testing and contact tracing. In their model, they have incorporated the control measures of condom use and antiretroviral therapy for the control of spread of HIV/AIDS in the susceptible population. They have presented a Forward-Backword sweep numerical method based on Adams-Bashforth-Moulton method for the solution of their model. Agrawal [36] formulated a fractional optimal control problem by using the Reimann-Liouville fractional derivatives and presented a numerical method for its solution. Bashir et al. [37] presented a fractional optimal control for a kinetic model and provided a numerical scheme for its solution.

Going by the antecedents, we have seen clearly that modeling of physical and real-life scenarios with the fractional order derivatives is much more accurate when compared with the integer order cases. This assertion has been demonstrated a number of research papers, monographs and books, see for example [38], [39], [40], [41]. In view of these achievements, we are motivated in this research work by modeling the control and analysis of SEI₁I₂R dynamics of HIV disease transmission using the Caputo fractional order operator which is most suited for modeling the biological and physical facts [42], [43], [44], [45], [46], [47]. The choice of using the Caputo derivative is due to the fact that, if the given function is a constant, then the Caputo derivative of that function gives zero. Primarily, the Caputo operator computes an ordinary differential equation, followed by a fractional integral to obtain the desired order of fractional derivative. More importantly, the Caputo fractional differential equation (FDO) permits the use of local initial conditions to be included in the derivation of the model.

In the present paper, we propose and analyze a fractional optimal control problem, in which the state and co-state equations are given in terms of the Caputo fractional derivatives. This approach simplifies the use of fractional numerical methods to solve the state and co-state equations. Fractional optimal control problems can be regarded as a generalization of classic optimal control problems for which the dynamics of the control system are described by fractional differential equations. We incorporate into the model time dependent controls such as condom use for exposed individuals, treatment for infected female sex workers, awareness about the disease among unaware infectives and behavioral change for susceptibles in order to reduce the risk of the spread of HIV/AIDS disease. Conditions for fractional optimal control of the disease are derived and the state and co-state equations are characterized by Caputo fractional derivatives. The numerical solution of the proposed fractional optimal control problem is obtained by using generalized Adams-Bashforth-Moulton method. Furthermore, the efficacy of order of fractional derivative, the control strategies and the value of objective functional is investigated.

The structure of the paper is designed as: in the next Section 2, some preliminary results required for the formulation of mathematical model is provided. Development of the proposed mathematical model and its well-posedness is discussed in Section 3. In Section 4, we discuss the mathematical analysis of the proposed fractional order SEI₁I₂R epidemic model along with equilibrium points and the stability of equilibrium points. In Section 5, the fractional optimal control problem is formulated and discussed. Also, in this Section, the necessary conditions for the optimality of proposed fractional optimal control problem is provided. Furthermore, in Section 6, application of the generalized Adams-Bashforth-Moulton method is performed on the proposed model and the numerical simulations are done to validate the analytical studies. In Section 7, numerical results are given to illustrate the capability of generalized Adams-Bashforth-Moulton method and the behavior of the obtained solutions is also discussed in this section. Finally, Section 8 concludes all the major findings of the present research study.

2. Mathematical preliminaries

Researchers have continuously extended the definitions of fractional order derivatives like the Riemann-Liouville, the Caputo, Caputo-Fabrizio, Atangana-Baleanu, the Grunwald-Letnikov, the Weyl, the Marchaud, the Riesz, and the Miller and Ross [48], [49], [50], [51], [52]. Recently, many new definitions of fractional derivative [53] have hugely evolved, going from the derivatives with nonsingular kernel and new Riemann-Liouville fractional derivative without singular kernel to the two-parameter derivatives with non-singular and non-local kernel [54], [55], [56].

Definition 2.1

A real function ψ(t), t > 0 is said to be in the space $C_{\eta },\eta \in \mathcal{R},$ if there exists a real number l > η, such that $\psi \left(t\right)=t^l{\psi }_1\left(t\right),$ where ψ ₁(t) ∈ C[0, ∞) and it is said to be in the space $C_{\eta }^n,$ if and only if ψⁿ(t) ∈ C_η, n ∈ N.

Definition 2.2

The Riemann-Liouville form of fractional integral operator ${}_0^{RL}{D}_t^{-\kappa }$of order κ > 0 for a function $\psi :{\mathcal{R}}^{+}\to \mathcal{R}$ is defined as

$${}_0^{RL}{D}_t^{-\kappa }\psi \left(t\right)=\frac{1}{\Gamma \left(\kappa \right)}\underset{0}{\overset{t}{\int }}{(t-\epsilon )}^{\kappa -1}\psi \left(\epsilon \right)d\epsilon ,t>0,$$ (1)

or

$$\begin{array}{c}{}_0^{RL}{I}_t^{\kappa }\psi \left(t\right)=\frac{1}{\Gamma \left(\kappa \right)}\underset{0}{\overset{t}{\int }}{(t-\epsilon )}^{\kappa -1}\psi \left(\epsilon \right)d\epsilon ,t>0,\hfill \\ {}_0^{RL}{I}_t^0\psi \left(\epsilon \right)=\psi \left(\epsilon \right),\hfill \end{array}$$ (2)

where κ > 0 and Γ(.) is a well-known Gamma function.

Definition 2.3

The Riemann-Liouville form of fractional derivative of ψ(t) order κ > 0 is defined as

$$\begin{array}{c}\hfill {}_0^{\mathit{RL}}{D}_t^{\kappa }\psi \left(t\right)=\{\begin{array}{c}{\displaystyle \frac{1}{\Gamma (n-\kappa )}{\left(\frac{d}{\mathit{dt}}\right)}^n{\underset{0}{\int }}^t\frac{\psi \left(\epsilon \right)}{{(t-\epsilon )}^{\kappa -n+1}}d\epsilon ,}\hfill \\ 0\le n-1<\kappa <n,n=\left[\kappa \right],n\in N,\hfill \\ {\displaystyle {\left(\frac{d}{\mathit{dt}}\right)}^n\psi \left(t\right),\kappa =n,n\in N.}\hfill \end{array}\end{array}$$ (3)

Definition 2.4

The Caputo fractional derivative of ψ(t) order κ > 0 is defined as

$$\begin{array}{c}\hfill {}_0^C{D}_t^{\kappa }\psi \left(t\right)=\{\begin{array}{c}{\displaystyle \frac{1}{\Gamma (n-\kappa )}{\underset{0}{\int }}^t\frac{{(d/\mathit{dt})}^n\psi \left(\epsilon \right)}{{(t-\epsilon )}^{\kappa -n+1}}d\epsilon ,}\hfill \\ 0\le n-1<\kappa <n,n=\left[\kappa \right],n\in N,\hfill \\ {\displaystyle {\left(\frac{d}{\mathit{dt}}\right)}^n\psi \left(t\right),\kappa =n,n\in N.}\hfill \end{array}\end{array}$$ (4)

where the operator ${}_0^C{D}_t^{\kappa }$ satisfies the following two basic properties:

$$\begin{array}{ccc}& & {}_0^C{D}_t^{\kappa }{}_0^{RL}{I}_t^{\kappa }\psi \left(t\right)=\psi \left(t\right)\text{and}{}_0^{RL}{I}_t^{\kappa }{}_0^C{D}_t^{\kappa }\psi \left(t\right)\hfill \\ & & =\psi \left(t\right)-\sum _{\vartheta =0}^{n-1}\frac{{\psi }^{\left(\vartheta \right)}\left(a\right)}{\vartheta !}{(t-a)}^{\vartheta },t>a.\hfill \end{array}$$

The definition 2.3 and definition 2.4 are not equivalent to each other, and their difference is expressed by

$${}_0^C{D}_t^{\kappa }\psi \left(t\right)={}_0^{RL}{D}_t^{\kappa }\psi \left(t\right)-\sum _{x=0}^{n-1}{r}_x^{\kappa }\left(t\right){\psi }^{\left(x\right)}\left(0\right),r_x^{\kappa }\left(t\right)=\frac{t^{x-\kappa }}{\Gamma \left(x+1-\kappa \right)}$$

The Caputo operator ${}_0^C{D}_t^{\kappa },$ has advantages for differential equations with initial values. In the case of Riemann-Liouville and Caputo derivatives, respectively, the initial values are usually given as [57]

$${}_0^{RL}{D}_t^{\kappa }\psi \left(0\right)=b_v,{}_0^C{D}_t^{\kappa }\psi \left(0\right)=b_v,v=1,2,3...,n$$

A direct definition of the fractional derivative $D_t^{\kappa }\psi \left(t\right),$ is based on finite differences of an equidistant grid in [0, t]. Assume that the function $D_t^{\kappa }\psi \left(t\right),$ satisfies some smoothness conditions in every finite interval (0, t), t ≤ T. Choosing the grid

$0={\tau }_0<{\tau }_1<...<{\tau }_{n+1}=t=\left(n+1\right)u,{\tau }_{n+1}-{\tau }_n=u,$ and using the classical notation of finite differences,

$$\frac{1}{u^{\kappa }}{\Delta }_u^{\kappa }\psi \left(t\right)=\frac{1}{u^{\kappa }}\left(\psi \left({\tau }_{n+1}\right)-\sum _{v=1}^{n+1}{c}_v^{\kappa }\psi \left({\tau }_{n+1-v}\right)\right)$$

where

$$c_v^{\kappa }=-{\left(1\right)}^{v-1}\left(\begin{array}{c}\kappa \\ v\end{array}\right)$$

Definition 2.5

The Laplace transform of the Caputo fractional derivative of ψ(t) order κ > 0 is defined as

$$L\left[{}_0^C{D}_t^{\kappa }\psi \left(t\right)\right]=s^{\kappa }\Psi \left(s\right)-\sum _{\vartheta =0}^{n-1}{\psi }^{\left(\vartheta \right)}\left(0\right)s^{\kappa -\vartheta -1}$$ (5)

Definition 2.6

The Laplace transform of the function $t^{{\kappa }_1-1}{E}_{\kappa ,{\kappa }_1}\left(\pm \lambda t^{\kappa }\right)$ is defined as

$$L\left[t^{{\kappa }_1-1}{E}_{\kappa ,{\kappa }_1}\left(\pm \lambda t^{\kappa }\right)\right]=\frac{s^{\kappa -{\kappa }_1}}{s^{\kappa }\mp \lambda }$$ (6)

where $E_{\kappa ,{\kappa }_1}$ is the two-parameter Mittage-Leffler function with κ, κ ₁ > 0.

Further, the Mittage-Leffler function satisfies the following equation [58]

$$E_{\kappa ,{\kappa }_1}\left(q\right)=q.E_{\kappa ,\kappa +{\kappa }_1}\left(q\right)+\frac{1}{\Gamma \left({\kappa }_1\right)}.$$ (7)

3. Model formulation

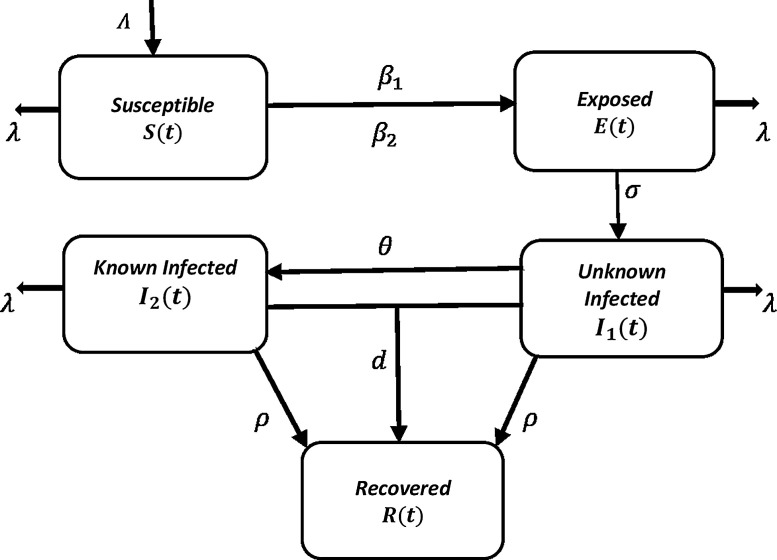
To describe the transmission dynamics of HIV epidemics, we have generalized the basic SIR epidemic model by including more compartments, to one in which population is divided into five sub-classes, the susceptible population S(t), the exposed population E(t), the infective population that don't know they are infected I ₁(t), the infective population that know they are infected I ₂(t), by means of medical screening or otherwise and recovered population R(t). The proposed model is considered as the generalization of the original Kermack-Mckendrick model [8], where only three compartments were considered, but here the exposed compartment is included contains those susceptible males in the population who have sexual intercourse with the female sex workers as a result by having sexual contact they are exposed to the infection. Furthermore, the infected class is divided into two sub-classes namely infected female sex workers who are unaware about their disease status and the infected female sex workers who knows their disease status. Thus, the model takes the following form [3,15,18].

$$\begin{array}{c}\hfill \{\begin{array}{c}{\displaystyle \frac{\mathit{dS}\left(t\right)}{\mathit{dt}}=\Lambda -S\left(t\right)({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right))-\lambda S\left(t\right)}\hfill \\ {\displaystyle \frac{\mathit{dE}\left(t\right)}{\mathit{dt}}=S\left(t\right)({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right))-(\lambda +\sigma )E\left(t\right)}\hfill \\ {\displaystyle \frac{d{I}_1\left(t\right)}{\mathit{dt}}=\sigma E\left(t\right)-(\rho +\lambda +\theta )I_1\left(t\right)}\hfill \\ {\displaystyle \frac{d{I}_2\left(t\right)}{\mathit{dt}}=\theta I_1\left(t\right)-(\lambda +\rho )I_2\left(t\right)}\hfill \\ {\displaystyle \frac{\mathit{dR}\left(t\right)}{\mathit{dt}}=\rho (I_1\left(t\right)+I_2\left(t\right))-(d+\lambda )R\left(t\right)}\hfill \end{array}\end{array}$$ (8)

For the understanding of HIV disease dynamics, the total population N(t) is divided into five sub-population compartments namely susceptible, exposed, infected but unaware, infected but aware and recovered such that $N\left(t\right)=S\left(t\right)+E\left(t\right)+I_1\left(t\right)+I_2\left(t\right)+R\left(t\right)$ for all t. The following description is associated to the above classical model: the susceptibles are recruited at a rate Λ, β ₁ is the per capita rate for susceptibles individuals with unaware infectives, β ₂ is the per capita rate for susceptibles individuals with aware infectives, λ is the natural death rate unrelated to AIDS, σ is the break through into infected class, θ is the rate of unaware infectives to become aware infectives by screening or testing, ρ is the rate by which types of infectives develop AIDS and d is the AIDS related death rate. It may further be noted that $N^{\prime }\left(t\right)=S^{\prime }\left(t\right)+E^{\prime }\left(t\right)+I_1^{\prime }\left(t\right)+I_2^{\prime }\left(t\right)+R^{\prime }\left(t\right)=0$ reveals constancy of total population.

We further extend the above ordinary differential model to the following fractional order system of order κ, with σ, ρ > 0 being the rate that exposed individuals become infectious and recovery rate, respectively and λ ≥ 0 being the infection related death rate. The purpose of considering the fractional order case is the significant uniqueness of these varieties of fractional order systems with non-local characteristics (memory) and hereditary properties that have not been seen with the integer-order differential operators which widely exists in biology. Also, using fractional order differential equations can help us to reduce the errors arising from the neglected parameters in modelling real life phenomena. In each case, we replace the ordinary derivative by a fractional derivative. Thus, our proposed fractional order model for HIV disease transmission has the form

$$\begin{array}{c}\hfill \{\begin{array}{c}{\displaystyle {}_0^C{D}_t^{\kappa }S\left(t\right)=\Lambda -S\left(t\right)({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right))-\lambda S\left(t\right)}\hfill \\ {\displaystyle {}_0^C{D}_t^{\kappa }E\left(t\right)=S\left(t\right)({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right))-(\lambda +\sigma )E\left(t\right)}\hfill \\ {\displaystyle {}_0^C{D}_t^{\kappa }{I}_1\left(t\right)=\sigma E\left(t\right)-(\rho +\lambda +\theta )I_1\left(t\right)}\hfill \\ {\displaystyle {}_0^C{D}_t^{\kappa }{I}_2\left(t\right)=\theta I_1\left(t\right)-(\lambda +\rho )I_2\left(t\right)}\hfill \\ {\displaystyle {}_0^C{D}_t^{\kappa }R\left(t\right)=\rho (I_1\left(t\right)+I_2\left(t\right))-(d+\lambda )R\left(t\right)}\hfill \end{array}\end{array}$$ (9)

subject to the initial conditions

$$S\left(0\right)=S_0,E\left(0\right)=E_0,I_1\left(0\right)=I_{1,0},I_2\left(0\right)=I_{2,0}\text{and}R\left(0\right)=R_0$$ (10)

where 0 < κ ≤ 1, $N\left(t\right)=S\left(t\right)+E\left(t\right)+I_1\left(t\right)+I_2\left(t\right)+R\left(t\right),\left(S\left(t\right),E\left(t\right),I_1\left(t\right),I_2\left(t\right),R\left(t\right)\right)\in {\Re }_{+}^5$ and if $\kappa =1$, then system (9) reduces to an integer order system (8). It is clear that the variable R(t) does not appear in the first four equations, thus it is meaningful to consider the reduced system (9) as:

$$\begin{array}{c}\hfill \{\begin{array}{c}{\displaystyle {}_0^C{D}_t^{\kappa }S\left(t\right)=\Lambda -S\left(t\right)({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right))-\lambda S\left(t\right)}\hfill \\ {\displaystyle {}_0^C{D}_t^{\kappa }E\left(t\right)=S\left(t\right)({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right))-(\lambda +\sigma )E\left(t\right)}\hfill \\ {\displaystyle {}_0^C{D}_t^{\kappa }{I}_1\left(t\right)=\sigma E\left(t\right)-(\rho +\lambda +\theta )I_1\left(t\right)}\hfill \\ {\displaystyle {}_0^C{D}_t^{\kappa }{I}_2\left(t\right)=\theta I_1\left(t\right)-(\lambda +\rho )I_2\left(t\right)}\hfill \end{array}\end{array}$$ (11)

subject to the positive initial conditions

$$S\left(0\right)=S_0,E\left(0\right)=E_0,I_1\left(0\right)=I_{1,0},I_2\left(0\right)=I_{2,0}$$ (12)

Here, it is assumed that the functions S(t), E(t), I ₁(t), I ₂(t), R(t) and their Caputo fractional derivatives are continuous at t ≥ 0. Again, since ${}_0^C{D}_t^{\kappa }N\left(t\right)=0,$ the population size is constant. To start, the existence, uniqueness, and non-negativity of the solution of system (11) are analyzed. The schematic diagram of the proposed fractional order SEI₁I₂R epidemic model (9) is shown in Fig. 1 .

Fig. 1.

Schematic diagram of the fractional order HIV epidemic model.

4. Analysis of the model

In this section, we first prove the existence and uniqueness of positive solution, then the basic reproduction number and the existence conditions for both equilibria (disease-free equilibrium and endemic equilibrium) are obtained, finally, the conditions for the stability of both the equilibria are obtained.

4.1. Positivity and boundedness

Let us denote ${\mathcal{R}}_{+}^4=\{\psi \left(t\right)\in {\mathcal{R}}^4:\psi \left(t\right)\ge 0\}$ and let $\psi \left(t\right)={\left[S\left(t\right),E\left(t\right),I_1\left(t\right),I_2\left(t\right)\right]}^T.$ For the proof of the main theorem about the non-negativity of the solutions, we recall the following lemma [3,8,15].

Lemma 4.1

(Generalized Mean Value Theorem [3,8,15]). Let ψ(t) ∈ C[a, b] and Caputo fractional derivative ${}_0^C{D}_t^{\kappa }\psi \left(t\right)\in C\left(a,b\right]$ for 0 < κ ≤ 1, then we have

$$\psi \left(t\right)=\psi \left(a\right)+\frac{1}{\Gamma \left(\kappa \right)}{}_0^C{D}_t^{\kappa }\psi \left(ϵ\right){(t-a)}^{\kappa }$$

with $0\le ϵ\le t,\forall t\in \left(a,b\right].$

Remark 4.1

If ψ(t) ∈ C[0, b] and Caputo fractional derivative ${}_0^C{D}_t^{\kappa }\psi \left(t\right)\in \left(0,b\right]$ for 0 < κ ≤ 1. It is clear from the lemma 4.1 that if ${}_0^C{D}_t^{\kappa }\psi \left(t\right)\ge 0,\forall t\in \left(0,b\right],$ then the function ψ(t) is non-decreasing and if ${}_0^C{D}_t^{\kappa }\psi \left(t\right)\le 0,\forall t\in \left(0,b\right],$ then the function ψ(t) is non-increasing for all t ∈ [0, b].This completes the proof.□

Theorem 4.1

There is a unique solution $\psi \left(t\right)={\left[S\left(t\right),E\left(t\right),I_1\left(t\right),I_2\left(t\right)\right]}^T$for the initial value problem given by (11) along initial conditions (12) on t ≥ 0 in (0, κ) and the solution will remain in ${\mathcal{R}}_{+}^4.$ Furthermore, the solutions are all bounded.

Proof

According to Lin [58] from the Theorem 3.2 [58] and Remark 3.2 [58], we can determine the solution on (0, ∞) by solving the model (11) along initial conditions (12) which is not only existent but also unique. Subsequently, we have to explain the non-negative domain ${\mathcal{R}}_{+}^4,$ is positively invariant region. From model (11), we find

$${}_0^C{D}_t^{\kappa }S\left(t\right){|}_{S=0}=\Lambda >0,{}_0^C{D}_t^{\kappa }E\left(t\right){|}_{E=0}=S\left(t\right)\left[{\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right]\ge 0,$$

$${}_0^C{D}_t^{\kappa }{I}_1\left(t\right){|}_{I_1=0}=\sigma E\left(t\right)\ge 0,{}_0^C{D}_t^{\kappa }{I}_2\left(t\right){|}_{I_2=0}=\theta I_1\left(t\right)\ge 0,$$

On each hyperplane bounding the non-negative orthant, the vector field points into ${\mathcal{R}}_{+}^4.$ Furthermore, from system (11)

$${}_0^C{D}_t^{\kappa }N\left(t\right)+\lambda N\left(t\right)\le \Lambda$$

Thus, by Lemma 4.1, in the case of HIV infection, the total population N(t), i.e., the subpopulations S(t), E(t), I ₁(t) and I ₂(t) are bounded.

By positivity means the population survives and boundedness refers as a natural restriction to growth as a consequence of limited resources. This completes the proof of the theorem 4.1. □

Therefore, the biologically feasible region for the system (9) is

$$\begin{array}{c}\hfill \Psi =\left\{\begin{array}{c}\left(S\left(t\right),E\left(t\right),I_1\left(t\right),I_2\left(t\right)\right)\hfill \\ \in {\mathcal{R}}_{+}^4|0<S\left(t\right)+E\left(t\right)+I_1\left(t\right)+I_2\left(t\right)\le \frac{\Lambda }{\lambda }\hfill \end{array}\right\}\end{array}$$

4.2. Existence of equilibria and their stability

For the equilibrium points, setting the right-hand side of the system (11) equal to zero, we obtain equilibrium points as

$$\begin{array}{c}\hfill \{\begin{array}{c}{\displaystyle \Lambda -S\left(t\right)({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right))-\lambda S\left(t\right)=0}\hfill \\ {\displaystyle S\left(t\right)({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right))-(\lambda +\sigma )E\left(t\right)=0}\hfill \\ {\displaystyle \sigma E\left(t\right)-(\rho +\lambda +\theta )I_1\left(t\right)=0}\hfill \\ {\displaystyle \theta I_1\left(t\right)-(\lambda +\rho )I_2\left(t\right)=0}\hfill \end{array}\end{array}$$ (13)

After simplification, the system (13) gives the disease-free equilibrium point Đ${}^0=\left(\frac{\Lambda }{\lambda },0,0,0\right)$ and the endemic equilibrium point Đ${}^{*}=\left(S^{*},E^{*},I_1^{*},I_2^{*}\right)$, where

$$S^{*}=\frac{\left(\lambda +\rho \right)\left(\lambda +\sigma \right)\left(\lambda +\rho +\theta \right)}{\sigma \left({\beta }_1\left(\lambda +\rho \right)+{\beta }_2\theta \right)},E^{*}=\frac{\left(\rho +\lambda +\theta \right)}{\sigma }{I}_1^{*},I_1^{*}=\frac{\Lambda \sigma }{\left(\lambda +\sigma \right)\left(\lambda +\rho +\theta \right)}+\frac{\lambda \left(\lambda +\rho \right)}{{\beta }_1\left(\lambda +\rho \right)+{\beta }_2\theta }$$

$$I_2^{*}=\frac{\theta }{\left(\lambda +\rho \right)}{I}_1^{*}$$

Thus, the proposed nonlinear fractional order SEI ₁ I ₂ R epidemic model has at most two equilibria namely disease-free equilibrium point Đ${}^0=\left(\frac{\Lambda }{\lambda },0,0,0\right)$ and the endemic equilibrium point Đ${}^{*}=\left(S^{*},E^{*},I_1^{*},I_2^{*}\right)$.

In order to study the local stability of the disease-free equilibrium, we first compute the basic reproduction number by using next generation matrix method [61], [62], [63], [64]. Let ${\phi }^{\prime }={\left(E,I_1,I_2,S\right)}^T.$ System (11) can be written as

$${\phi }^{\prime }=\mathcal{F}\left(\phi \right)-\mathcal{V}\left(\phi \right)$$

where

$$\begin{array}{ccc}\hfill \mathcal{F}\left(\phi \right)& =& \left(\begin{array}{c}\begin{array}{c}S\left(t\right)\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)\\ 0\\ 0\end{array}\\ 0\end{array}\right),\mathcal{V}\left(\phi \right)\hfill \\ & =& \left(\begin{array}{c}\begin{array}{c}\left(\lambda +\sigma \right)E\left(t\right)\\ \left(\rho +\lambda +\theta \right)I_1\left(t\right)-\sigma E\left(t\right)\\ \left(\lambda +\rho \right)I_2\left(t\right)-\theta I_1\left(t\right)\end{array}\\ S\left(t\right)\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)+\lambda S\left(t\right)-\Lambda \end{array}\right)\hfill \end{array}$$

By the next generation matrix method, the matrices Ғ and Ѵ at the disease-free equilibrium point Đ⁰ are obtained by

$$\Gamma =\left[\frac{\partial {\mathcal{F}}_p\left({-D}^0\right)}{\partial y_m}\right]\text{and}\mathcal{V}=\left[\frac{\partial {\mathcal{V}}_p\left({-D}^0\right)}{\partial y_m}\right],1\le p,m\le 4,$$

where Ғ is non-negative and $\mathcal{V}$ is a non-singular M-matrix.

Therefore, the basic reproduction number denoted by ${\mathcal{R}}_0$ which is considered as the spectral radius of the next generation matrix $\Gamma {\mathcal{V}}^{-1}$ at the disease-free equilibrium Đ⁰ is thus given by

$${\mathcal{R}}_0=\frac{\Lambda \left({\beta }_1\left(\lambda +\rho \right)\left(\lambda +\sigma \right)+{\beta }_2\theta \left(\lambda +\sigma \right)\right)}{\lambda \left(\lambda +\sigma \right)\left(\lambda +\rho \right)\left(\rho +\lambda +\theta \right)}$$

It shows that if ${\mathcal{R}}_0<1$, then the disease does not spread in the population and the infection dies. On the other hand, if ${\mathcal{R}}_0>1$, then the disease persists in the whole population.

4.3. Local stability of equilibria

Now, we will discuss the local stability analysis of equilibrium points. For this, we state the results in the form of theorems and prove them.

Theorem 4.2

The disease-free equilibrium Đ⁰ of proposed fractional order SEI₁I₂R epidemic model is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$.

Proof

To prove the above theorem 4.2, the general Jacobian matrix and the matrices corresponding to each equilibrium point will be obtained. Therefore, the Jacobian matrix is given by

$$\Omega =\left[\begin{array}{cccc}-({\beta }_1{I}_1+{\beta }_2{I}_2)-\lambda & 0& -{\beta }_{1}S& -{\beta }_{2}S\\ {\beta }_1{I}_1+{\beta }_2{I}_2& -\left(\lambda +\sigma \right)& {\beta }_{1}S& {\beta }_{2}S\\ 0& \sigma & -\left(\rho +\lambda +\theta \right)& 0\\ 0& 0& \theta & -\left(\lambda +\rho \right)\end{array}\right]$$

Now at the disease-free equilibrium Đ⁰,

$$\Omega \left({-\mathrm{D}}^0\right)=\left[\begin{array}{cccc}-\lambda & 0& -\frac{\Lambda }{\lambda }{\beta }_1& -\frac{\Lambda }{\lambda }{\beta }_2\\ 0& -\left(\lambda +\sigma \right)& \frac{\Lambda }{\lambda }{\beta }_1& \frac{\Lambda }{\lambda }{\beta }_2\\ 0& \sigma & -\left(\rho +\lambda +\theta \right)& 0\\ 0& 0& \theta & -\left(\lambda +\rho \right)\end{array}\right]$$

Therefore, by the Routh-Hurwitz stability conditions for fractional order systems [65], the necessary and sufficient condition

$$\left|\arg \left(eig\left(\Omega \right)\right)\right|=\left|\arg \left({\gamma }_i\right)\right|>\kappa \frac{\pi }{2}$$ (14)

for various fractional order models. Therefore, the disease-free equilibrium of system (11) is asymptotically stable if all of the eigenvalues, ${\gamma }_i,i=1,2,3,4,$ of $\Omega \left({-D}^0\right)$ satisfy the condition (14).

Hence, a sufficient condition for the local asymptotic stability of the equilibrium points is that the eigenvalues ${\gamma }_i,i=1,2,3,4,$ of the Jacobian matrix $\Omega \left({-D}^0\right)$ satisfy the condition $|\arg \left({\gamma }_i\right)|>\kappa \frac{\pi }{2}.$ This confirms that fractional order differential equations are, at least, as stable as their integer order counterpart. By solving the characteristic equation, the eigenvalues can be obtained as

$$\det \left(\Omega \left({-D}^0\right)-\gamma I\right)=0$$

The simplification allows us to get the following algebraic equation

$$\left(\lambda +\gamma \right)\left(\lambda +\rho +\gamma \right)\left({\gamma }^2+\left({\delta }_1+{\delta }_2\right)\gamma +{\delta }_1{\delta }_2-{\delta }_3\right)=0$$

where ${\delta }_1=\left(\lambda +\sigma \right)$, ${\delta }_2=\left(\rho +\lambda +\theta \right)$ and ${\delta }_3=\frac{\Lambda \sigma }{\lambda }{\beta }_1.$

If ${\mathcal{R}}_0<1$, then δ ₃ > 0 and also

$$\lambda \left(\lambda +\sigma \right)\left(\lambda +\rho \right)\left(\rho +\lambda +\theta \right)>\Lambda \left({\beta }_1\left(\lambda +\rho \right)\left(\lambda +\sigma \right)+{\beta }_2\theta \left(\lambda +\sigma \right)\right)$$

This implies,

$$\left(\lambda +\sigma \right)\left(\rho +\lambda +\theta \right)>\frac{\Lambda \sigma }{\lambda }{\beta }_1$$

Therefore, the roots of the characteristic equation are

$${\gamma }_1=-\lambda ,{\gamma }_2=-\left(\lambda +\rho \right),$$

$${\gamma }_{3,4}=\frac{-\left({\delta }_1+{\delta }_2\right)\pm \sqrt{{\left({\delta }_1+{\delta }_2\right)}^2-4\left({\delta }_1{\delta }_2-{\delta }_3\right)}}{2},$$

because ${\delta }_1+{\delta }_2>0\text{and}$ δ ₁ δ ₂ > δ ₃, all of the eigenvalues γ_i for $i=1,2,3,4,$ satisfy the condition given by (14). Therefore, all the eigenvalues have negative real parts if ${\mathcal{R}}_0<1$. This completes the proof of the theorem 4.2. □

In the next theorem 4.3, we discuss the local asymptotic stability of the endemic equilibrium of the system given by (11).

Theorem 4.3

The endemic equilibrium Đ* is locally asymptotically stable whenever ${\mathcal{R}}_0>1$ and unstable otherwise.

Proof

The Jacobian matrix of the system (11) evaluated at endemic equilibrium Đ* is given as

$$\Omega \left({-\mathrm{D}}^{*}\right)=\left[\begin{array}{cccc}{\beta }_1{I}_1^{*}+{\beta }_2{I}_2^{*}-\lambda & 0& -{\beta }_1{S}^{*}& -{\beta }_2{S}^{*}\\ {\beta }_1{I}_1^{*}+{\beta }_2{I}_2^{*}& -\left(\lambda +\sigma \right)& {\beta }_1{S}^{*}& {\beta }_2{S}^{*}\\ 0& \sigma & -\left(\rho +\lambda +\theta \right)& 0\\ 0& 0& \theta & -\left(\lambda +\rho \right)\end{array}\right]$$

The characteristic equation of the linearized system is in the form

$$\mathcal{C}\left(\gamma \right)=-\left(\lambda +\rho +\gamma \right)-P\left(\gamma \right)=0$$

with $-\mathrm{P}\left(\gamma \right)={\gamma }^3+{\vartheta }_1{\gamma }^2+{\vartheta }_2\gamma +{\vartheta }_3$, where

$${\vartheta }_1=\left(3\lambda +\sigma +\rho +\theta -{\beta }_1{I}_1^{*}-{\beta }_2{I}_2^{*}\right),$$ (15)

$$\begin{array}{ccc}\hfill {\vartheta }_2& =& ({\lambda }^2+\lambda \sigma -{\beta }_1{I}_1^{*}\left(\lambda +\sigma \right)-{\beta }_1{I}_1^{*}\left(\rho +\lambda +\theta \right)-{\beta }_2{I}_2^{*}\left(\lambda +\sigma \right)\hfill \\ & & -{\beta }_2{I}_2^{*}\left(\rho +\lambda +\theta \right)-\lambda \rho -\sigma \rho -\sigma \theta ),\hfill \end{array}$$ (16)

$$\begin{array}{ccc}\hfill {\vartheta }_3& =& ({\beta }_1{I}_1^{*}\left(\lambda +\sigma \right)\left(\rho +\lambda +\theta \right)-{\beta }_1^2\sigma I_1^{*}{S}^{*}\hfill \\ & & +{\beta }_2{I}_2^{*}\left(\lambda +\sigma \right)\left(\rho +\lambda +\theta \right)\hfill \\ & & -{\beta }_1{\beta }_2\sigma I_2^{*}{S}^{*}-\lambda \left(\lambda +\sigma \right)\left(\rho +\lambda +\theta \right)+{\beta }_1\lambda \sigma S^{*}),\hfill \end{array}$$ (17)

Now, the discriminant of the polynomial $-\mathrm{P}\left(\gamma \right)={\gamma }^3+{\vartheta }_1{\gamma }^2+{\vartheta }_2\gamma +{\vartheta }_3$ is described by [3,12,15]

$$D\left(-\mathrm{P}\right)=18{\vartheta }_1{\vartheta }_2{\vartheta }_3+{\left({\vartheta }_1{\vartheta }_2\right)}^2-4{\vartheta }_3{\vartheta }_1^2-4{\vartheta }_2^2-27{\vartheta }_3^2$$ (18)

and using the construction of results by Ahmed et al. [19,66], following fractional Routh-Hurwitz conditions associated with are observed. We have the following result.

Corollary 4.1

The positive equilibrium point Đ* of the system (11) is asymptotically stable for $\mathcal{R}>1,$ if one of the following conditions holds for polynomial -P(γ) and coefficients ϑ₁, ϑ₂, ϑ₃ which are given by (15),(16),(17) respectively.

• iIf D(-P)  > 0, then the necessary and sufficient condition for the equilibrium point to be locally asymptotically stable is ϑ₁ > 0, ϑ₃ > 0, ϑ₁ϑ₂ > ϑ₃,
• iiIf D(-P) < 0,ϑ₁ ≥ 0, ϑ₂ ≥ 0, ϑ₃ > 0, then the equilibrium point is locally asymptotically stable if $\kappa <\frac{2}{3},$
• iiiIf D(-P) < 0, ϑ₁ < 0, ϑ₂ < 0 and $\kappa >\frac{2}{3},$ then all roots of the Eq. (18) satisfy the condition $|\arg \left({\gamma }_i\right)|<\kappa \frac{\pi }{2},i=1,2,3,4.$

4.4. Global stability of equilibria

The global existence of the solution of the fractional differential equation always becomes a most important concern, which is carry out in the following section.

Theorem 4.4

[12,58], Assume that the function $\Phi :{\mathcal{R}}_{+}\times {\mathcal{R}}^4\to {\mathcal{R}}^4$satisfies the following conditions in the global space:

• 1)The function Φ(t, ψ(t)) is Lebesgue measurable with respect to t on $\mathcal{R}$.
• 2)The function Φ(t, ψ(t)) is continuous with respect to ψ(t) on ${\mathcal{R}}^4$.
• 3)The function $\frac{\partial \Phi \left(t,\psi \left(t\right)\right)}{\partial \psi }$ is continuous with respect to ψ(t) on ${\mathcal{R}}^4$.

$\Phi \left(t,\psi \left(t\right)\right)\le {\alpha }_1+{\alpha }_2\psi \left(t\right),$ for all most every $t\in \mathcal{R}$ and all $\psi \left(t\right)\in {\mathcal{R}}^4$.

Here α ₁,α ₂ are two positive constants and $\psi \left(t\right)={\left[S\left(t\right),E\left(t\right),I_1\left(t\right),I_2\left(t\right)\right]}^T.$ Then, the initial value problem

$$\begin{array}{c}\hfill \{\begin{array}{c}{\displaystyle \begin{array}{c}{\displaystyle {}_0^C{D}_t^{\kappa }\psi \left(t\right)=\Phi (t,\psi \left(t\right)),\kappa \in (0,1]}\hfill \end{array}}\hfill \\ {\displaystyle \psi \left(t_0\right)={\psi }_0,}\hfill \end{array}\end{array}$$ (19)

has a unique solution.

Theorem 4.5

The system (11) has a unique solution and the solution remains in ${\mathcal{R}}_{+}^4.$

Proof

From the Theorem 4.4, we obtain the unique solution on (0, ∞) by solving the system (11). Firstly, Lin [58] discussed the proof of theorem and shows that the solution is not only exist but also unique. In Theorem 4.1, we already proved that the solution of model (11) will remain in ${\mathcal{R}}_{+}^4.$

Lemma 4.2

([52,67]) Let $\psi \left(t\right)\in {\mathcal{R}}^{+}$ be a continuous and derivable function. Then, for any time instant t ≥ 0,

$${}_0^C{D}_t^{\kappa }\left(\psi \left(t\right)-{\psi }^{*}-{\psi }^{*}\ln \frac{\psi \left(t\right)}{{\psi }^{*}}\right)\le \left(1-\frac{{\psi }^{*}}{\psi \left(t\right)}\right){}_0^C{D}_t^{\kappa }\psi \left(t\right)$$ (20)

and

$$\frac{1}{2}{}_0^C{D}_t^{\kappa }{\psi }^2\left(t\right)\le \psi \left(t\right){}_0^C{D}_t^{\kappa }\psi \left(t\right)$$ (21)

where κ ∈ (0, 1).

Note that for $\kappa =1,$ the inequalities in (20) and (21) becomes equalities.

Now, we provide the global stability results of the equilibria in the following theorems by considering the Lyapunov direct method.

Theorem 4.6

The disease-free equilibrium ${-\mathrm{D}}^0=\left(\frac{\Lambda }{\lambda },0,0,0\right)$ of proposed model (11) is globally asymptotically stable in Ψ, if ${\mathcal{R}}_0\le 1$ and unstable when ${\mathcal{R}}_0>1$.

Proof

To prove this, we define a Lyapunov function ϕ ₁(t) given by

$${\varphi }_1\left(t\right)=\frac{1}{2S_0}{\left(S-S_0\right)}^2+E$$

This function is defined, continuous and positive definite for all t ≥ 0. It can be verified that the equality holds if and only if $S\left(t\right)=S_0,$ $E\left(t\right)=I_1\left(t\right)=I_2\left(t\right)=0$. Now, we have

$${}_0^C{D}_t^{\kappa }{\varphi }_1\left(t\right)=\frac{1}{2S_0}{}_0^C{D}_t^{\kappa }{\left(S-S_0\right)}^2+{}_0^C{D}_t^{\kappa }E\left(t\right)$$

$$\le \frac{1}{S_0}\left(S-S_0\right){}_0^C{D}_t^{\kappa }S\left(t\right)+{}_0^C{D}_t^{\kappa }E\left(t\right)$$

$$\begin{array}{ccc}& =& \frac{1}{S_0}\left(S-S_0\right)\left[\Lambda -\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)S\left(t\right)-\lambda S\left(t\right)\right]\hfill \\ & & +\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)S\left(t\right)-\left(\lambda +\sigma \right)E\left(t\right)\hfill \end{array}$$ (22)

Using the disease-free steady state condition of model (11), $S_0=\frac{\Lambda }{\lambda }$, we have from the equation (22) as

$$\begin{array}{ccc}& & {}_0^C{D}_t^{\kappa }{\varphi }_1\left(t\right)\le -\frac{\lambda }{S_0}{\left(S-S_0\right)}^2-\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)\left(S-S_0\right)S\left(t\right)\hfill \\ & & +\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)S\left(t\right)-\left(\lambda +\sigma \right)E\left(t\right)\hfill \end{array}$$

$$\begin{array}{ccc}& =& -\frac{\lambda }{S_0}{\left(S-S_0\right)}^2-\frac{\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)\left(S-S_0\right)S\left(t\right)}{S_0}\hfill \\ & & +\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)S\left(t\right)-\left(\lambda +\sigma \right)E\left(t\right)\hfill \end{array}$$

$$\begin{array}{ccc}& =& -\frac{\lambda }{S_0}{\left(S-S_0\right)}^2-\frac{\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right){\left(S-S_0\right)}^2}{S_0}\hfill \\ & & -\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)\left(S-S_0\right)+\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)S\left(t\right)\hfill \\ & & -\left(\lambda +\sigma \right)E\left(t\right)\hfill \end{array}$$

$$\begin{array}{ccc}& =& -\frac{\left(\lambda +{\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)}{S_0}{\left(S-S_0\right)}^2\hfill \\ & & -\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)S\left(t\right)+\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)S_0\hfill \end{array}$$

$$+\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)S\left(t\right)-\left(\lambda +\sigma \right)E\left(t\right)$$

$$\begin{array}{ccc}& =& -\frac{\left(\lambda +{\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)}{S_0}{\left(S-S_0\right)}^2\hfill \\ & & +\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)S_0-\left(\lambda +\sigma \right)E\left(t\right)\hfill \end{array}$$

$$\begin{array}{ccc}& =& -\frac{\left(\lambda +{\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)}{S_0}{\left(S-S_0\right)}^2\hfill \\ & & +\left({\beta }_1{I}_1\left(t\right)+{\beta }_2\frac{\theta I_1\left(t\right)}{\left(\lambda +\rho \right)}\right)\frac{\Lambda }{\lambda }-\frac{\left(\lambda +\sigma \right)\left(\lambda +\rho +\theta \right)}{\sigma }{I}_1\left(t\right)\hfill \end{array}$$

$$\begin{array}{ccc}& =& -\frac{\left(\lambda +{\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)}{S_0}{\left(S-S_0\right)}^2\hfill \\ & & +\frac{\sigma \Lambda }{\lambda }\left(\frac{{\beta }_1{I}_1\left(t\right)\left(\lambda +\rho \right)+{\beta }_2\theta I_1\left(t\right)}{\left(\lambda +\rho \right)}\right)-\left(\lambda +\sigma \right)\left(\lambda +\rho +\theta \right)I_1\left(t\right)\hfill \end{array}$$

$$\begin{array}{ccc}& =& -\frac{\left(\lambda +{\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)}{S_0}{\left(S-S_0\right)}^2\hfill \\ & & +\frac{\sigma }{\left(\lambda +\sigma \right)}\left(\frac{\Lambda \left({\beta }_1\left(\lambda +\sigma \right)\left(\lambda +\rho \right)+{\beta }_2\theta \left(\lambda +\sigma \right)\right)}{\lambda \left(\lambda +\sigma \right)\left(\lambda +\rho \right)\left(\lambda +\rho +\theta \right)}-1\right)I_1\left(t\right)\hfill \end{array}$$

This further implies,

$$\begin{array}{ccc}& & {}_0^C{D}_t^{\kappa }{\varphi }_1\left(t\right)\le -\frac{\left(\lambda +{\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)}{S_0}{\left(S-S_0\right)}^2\hfill \\ & & +\frac{\sigma }{\left(\lambda +\sigma \right)}\left({\mathcal{R}}_0-1\right)I_1\left(t\right)\le 0\hfill \end{array}$$

Therefore,

$${}_0^C{D}_t^{\kappa }{\varphi }_1\left(t\right)\le 0$$

It follows that if ${\mathcal{R}}_0<1$, then we have ${}_0^C{D}_t^{\kappa }{\varphi }_1\left(t\right){|}_{\left(11\right)}\le 0$. In addition, we know that ${}_0^C{D}_t^{\kappa }{\varphi }_1\left(t\right){|}_{\left(11\right)}=0$, if and only if $S\left(t\right)=S_0$ and $I_1\left(t\right)=0$.Substituting $I_1\left(t\right)=0$ into (11), one can directly obtain $E\left(t\right)=0$. Using $I_1\left(t\right)=E\left(t\right)=0$ again in (11), then $I_2\left(t\right)=0$. Therefore, the maximum invariant set for $\{\left(S,E,I_1,I_2\right)\in {\Omega }^0:{}_0^C{D}_t^{\kappa }{\varphi }_1\left(t\right){|}_{\left(11\right)}=0\}$ is the singleton set -D⁰. According to the LaSalle's invariance principle [61], [62], [63], [64], we know that all solutions in Ω⁰ converge to -D⁰.Therefore, the disease-free steady state of model (11) is globally asymptotically stable when ${\mathcal{R}}_0\le 1.$ This completes the proof of the theorem 4.6. □

Theorem 4.7

The endemic equilibrium Đ${}^{*}=\left(S^{*},E^{*},I_1^{*},I_2^{*}\right)$ of proposed model (11) is globally asymptotically stable in Ψ, when ${\mathcal{R}}_0>1$.

Proof

To prove this, we define a Lyapunov function ϕ ₂(t) given by

$$\begin{array}{ccc}\hfill {\varphi }_2\left(t\right)& =& \frac{1}{\lambda }\left(S-S^{*}-S^{*}\ln \frac{S}{S^{*}}\right)+\Theta \left(E-E^{*}-E^{*}\ln \frac{E}{E^{*}}\right)\hfill \\ & & +\frac{1}{\left(\rho +\lambda +\theta \right)}\left(I_1-I_1^{*}-I_1^{*}\ln \frac{I_1}{I_1^{*}}\right)\hfill \end{array}$$

where $\Theta =\frac{\left({\mathcal{R}}_0-1\right)}{\left(\lambda +\sigma \right)}>0$, when ${\mathcal{R}}_0>1.$

This function is defined, continuous and positive definite for all t ≥ 0. It can be verified that the equality holds if and only if $S\left(t\right)=S^{*},$ $E\left(t\right)=E^{*},I_1=I_1^{*}.$Now, we have from Lemma 4.2

$$\begin{array}{ccc}& & {}_0^C{D}_t^{\kappa }{\varphi }_2\left(t\right)={}_0^C{D}_t^{\kappa }[\frac{1}{\lambda }\left(S-S^{*}-S^{*}\ln \frac{S}{S^{*}}\right)\hfill \\ & & +\Theta \left(E-E^{*}-E^{*}\ln \frac{E}{E^{*}}\right)+\frac{1}{\left(\rho +\lambda +\theta \right)}\left(I_1-I_1^{*}-I_1^{*}\ln \frac{I_1}{I_1^{*}}\right)]\hfill \end{array}$$

$$\begin{array}{ccc}& & {}_0^C{D}_t^{\kappa }{\varphi }_2\left(t\right)\le \frac{1}{\lambda }\left(1-\frac{S^{*}}{S}\right){}_0^C{D}_t^{\kappa }S\left(t\right)\hfill \\ & & +\Theta \left(1-\frac{E^{*}}{E}\right){}_0^C{D}_t^{\kappa }E\left(t\right)+\frac{1}{\left(\rho +\lambda +\theta \right)}\left(1-\frac{I_1^{*}}{I_1}\right){}_0^C{D}_t^{\kappa }{I}_1\left(t\right)\hfill \end{array}$$

$$\begin{array}{ccc}& =& \frac{1}{\lambda }\left(1-\frac{S^{*}}{S}\right)\left[\Lambda -\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)S\left(t\right)-\lambda S\left(t\right)\right]\hfill \\ & & +\Theta \left(1-\frac{E^{*}}{E}\right)\left[\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)S\left(t\right)-\left(\lambda +\sigma \right)E\left(t\right)\right]\hfill \\ & & +\frac{1}{\left(\rho +\lambda +\theta \right)}\left(1-\frac{I_1^{*}}{I_1}\right)\left[\sigma E\left(t\right)-\left(\rho +\lambda +\theta \right)I_1\left(t\right)\right]\hfill \end{array}$$ (23)

Using the endemic conditions,

$$\Lambda -\left({\beta }_1{I}_1^{*}+{\beta }_2{I}_2^{*}\right)S^{*}=\lambda S^{*}$$

$$\left({\beta }_1{I}_1^{*}+{\beta }_2{I}_2^{*}\right)S^{*}=\left(\lambda +\sigma \right)E^{*}$$

$$\sigma E^{*}=\left(\rho +\lambda +\theta \right)I_1^{*}$$

$$\theta I_1^{*}=\left(\lambda +\rho \right)I_2^{*}$$

in equation (23), we get

$${}_0^C{D}_t^{\kappa }{\varphi }_2\left(t\right)\le -\frac{{\left(S-S^{*}\right)}^2}{S}-\frac{{\left(E-E^{*}\right)}^2}{E}\left({\mathcal{R}}_0-1\right)-\frac{{\left(I_1-I_1^{*}\right)}^2}{I_1}$$

This implies,

$${}_0^C{D}_t^{\kappa }{\varphi }_2\left(t\right)\le 0$$

It follows that if ${\mathcal{R}}_0>1$, then we have ${}_0^C{D}_t^{\kappa }{\varphi }_2\left(t\right){|}_{\left(11\right)}\le 0$. Therefore, ϕ ₂(t) is bounded and non-increasing. Further, the limit of ϕ ₂(t) exits as t → ∞. In addition, we know that ${}_0^C{D}_t^{\kappa }{\varphi }_2\left(t\right){|}_{\left(11\right)}=0$, if and only if $S\left(t\right)=S^{*},$ $E\left(t\right)=E^{*},I_1\left(t\right)=I_1^{*}$ and $I_2\left(t\right)=I_2^{*}$. Therefore, the maximum invariant set for $\{\left(S^{*},E^{*},I_1^{*},I_2^{*}\right)\in {\Omega }^{*}:{}_0^C{D}_t^{\kappa }{\varphi }_2\left(t\right){|}_{\left(11\right)}=0\}$ is the singleton set {Đ*}. According to the LaSalle's invariance principle [61], [62], [63], [64], we know that all solutions in Ω* converge to Đ*.Therefore, the endemic equilibrium of proposed model (11) is globally asymptotically stable when ${\mathcal{R}}_0>1.$ This completes the proof of the theorem 4.7. □

5. Fractional optimal problem

In this section, we extend the basic model (8) by including some particular control measures aimed at controlling the spread of the HIV infection and formulate the fractional optimal control problem by proposing the control objectives. The aim of the control measures is to reduce the infection in the population and thus there is the need to formulate the optimal control problem to achieve this goal. The first control function v ₁(t) represents the behavioral change for susceptibles which reduced the number of exposed by a factor $\left(1-v_1\left(t\right)\right)$. The control v ₁(t) is proposition of the susceptible individuals who change their sexual habits per unit of time. The second control function v ₂(t) is the use of condoms to the exposed individuals who are going to have sexual interaction with the female sex workers. The third control function v ₃(t) represent the enhancement of the strength of treatment for the infected individuals. The fourth control function v ₄(t) is the awareness source among the unaware infectives about their disease status. Under these control measures the proposed model (8) is modified as

$$\begin{array}{c}\hfill \{\begin{array}{c}{\displaystyle {}_0^C{D}_t^{\kappa }S\left(t\right)=\Lambda -(1-v_2)S\left(t\right)({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right))-(\lambda +v_1)S\left(t\right)}\hfill \\ {\displaystyle {}_0^C{D}_t^{\kappa }E\left(t\right)=(1-v_2)S\left(t\right)({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right))-(\lambda +\sigma )E\left(t\right)}\hfill \\ {\displaystyle {}_0^C{D}_t^{\kappa }{I}_1\left(t\right)=\sigma E\left(t\right)-(\rho +\lambda +\theta +v_4)I_1\left(t\right)}\hfill \\ {\displaystyle {}_0^C{D}_t^{\kappa }{I}_2\left(t\right)=\theta I_1\left(t\right)-(\lambda +\rho +v_3)I_2\left(t\right)}\hfill \\ {\displaystyle {}_0^C{D}_t^{\kappa }R\left(t\right)=\rho (I_1\left(t\right)+I_2\left(t\right))-(d+\lambda )R\left(t\right)+v_{1}S\left(t\right)}\hfill \\ \mathit{All}\mathit{formulas}\mathit{and}\mathit{models}\mathit{should}\mathit{be}\mathit{left}\mathit{aligned}\hfill \end{array}.\end{array}$$ (24)

with the non-negative initial conditions

$$S\left(0\right)=S_0,E\left(0\right)=E_0,I_1\left(0\right)=I_{1,0},I_2\left(0\right)=I_{2,0}\text{and}R\left(0\right)=R_0$$ (25)

The control is completely effective when $v_i\left(t\right)=1$ and the control is not effective when $v_i\left(t\right)=0$, for $i=1,2,3,4$ i.e., 0 ≤ v_i(t) < 1. Our focus is to minimize the number of exposed individuals under the cost of applying control measures which can be done by consider the following fractional optimal control problem to minimize the objective functional given by

$$\begin{array}{ccc}& & \gamma \left(v_1,v_2,v_3,v_4\right)\hfill \\ & & =\underset{0}{\overset{\tau }{\int }}\left(\mathbb{Q}E+\frac{{-\mathrm{p}}_1}{2}{v}_1^2\left(t\right)+\frac{{-\mathrm{p}}_2}{2}{v}_2^2\left(t\right)+\frac{{-\mathrm{p}}_3}{2}{v}_3^2\left(t\right)+\frac{{-\mathrm{p}}_4}{2}{v}_4^2\left(t\right)\right)dt\hfill \end{array}$$ (26)

subjected to the state system given in (24) along non-negative initial conditions (25). In Eq. (26), $\mathbb{Q}$ represent the positive weight constant of the exposed population, while -p₁, -p₂, -p₃, and -p₄ are positive weight constants for behavioral change, personal protection, treatment strategy and awareness source respectively. The terms $\frac{1}{2}{-\mathrm{p}}_1{v}_1^2,\frac{1}{2}{-\mathrm{p}}_2{v}_2^2,\frac{1}{2}{-\mathrm{p}}_3{v}_3^2\text{and}\frac{1}{2}{-\mathrm{p}}_4{v}_4^2$ describe the costs associated with the corresponding interventions. It is supposed that the costs are proportional to the square of the corresponding control function. Our objective of the fractional optimal control problem is to find out the optimal control functions $v_1^{*},$ $v_2^{*},v_3^{*},v_4^{*}$ such that

$$\mathrm{Y}\left(v_1^{*},v_2^{*},v_3^{*},v_4^{*}\right)=min\left\{\mathrm{Y}\left(v_1,v_2,v_3,v_4\right),\left(v_1,v_2,v_3,v_4\right)\in V\right\},$$ (27)

subjected to the state system given in (24), where the control set is defined as

$$\begin{array}{ccc}\hfill V& =& \{(v_1,v_2,v_3,v_4)|v_i\left(t\right)\text{is}\text{Lebesgue}\text{measuerable}\text{on}\left[0,1\right],\hfill \\ & & i=1,2,3,4\}.\hfill \end{array}$$ (28)

The Lagrangian Ɫ and Hamiltonian $\mathcal{H}$ for the fractional optimal problem (24)-(28) are respectively given by [35,[68], [69]]

$$-L\left(E,v_1,v_2,v_3,v_4\right)=\mathbb{Q}E+\frac{{-\mathrm{p}}_1}{2}{v}_1^2+\frac{{-\mathrm{p}}_2}{2}{v}_2^2+\frac{{-\mathrm{p}}_3}{2}{v}_3^2+\frac{{-\mathrm{p}}_4}{2}{v}_4^2$$ (29)

and

$$\begin{array}{ccc}& & \mathcal{H}=-L\left(E,v_1,v_2,v_3,v_4\right)+{\lambda }_S{}_0^C{D}_t^{\kappa }S\left(t\right)+{\lambda }_E{}_0^C{D}_t^{\kappa }E\left(t\right)\hfill \\ & & +{\lambda }_{I_1}{}_0^C{D}_t^{\kappa }{I}_1\left(t\right)+{\lambda }_{I_2}{}_0^C{D}_t^{\kappa }{I}_2\left(t\right)+{\lambda }_R{}_0^C{D}_t^{\kappa }R\left(t\right)\hfill \end{array}$$

This further implies,

$$\begin{array}{c}\hfill \begin{array}{c}\mathcal{H}=\mathbb{Q}E+\frac{{-\mathrm{p}}_1}{2}{v}_1^2+\frac{{-\mathrm{p}}_2}{2}{v}_2^2+\frac{{-\mathrm{p}}_3}{2}{v}_3^2+\frac{{-\mathrm{p}}_4}{2}{v}_4^2\hfill \\ +{\lambda }_S\left[\Lambda -\left(1-v_2\right)S\left(t\right)\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)-\left(\lambda +v_1\right)S\left(t\right)\right]\hfill \\ +{\lambda }_E\left[\left(1-v_2\right)S\left(t\right)\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)-\left(\lambda +\sigma \right)E\left(t\right)\right]\hfill \\ +{\lambda }_{I_1}\left[\sigma E\left(t\right)-\left(\rho +\lambda +\theta +v_4\right)I_1\left(t\right)\right]\hfill \\ +{\lambda }_{I_2}\left[\theta I_1\left(t\right)-\left(\lambda +\rho +v_3\right)I_2\left(t\right)\right]\hfill \\ +{\lambda }_R\left[\rho \left(I_1\left(t\right)+I_2\left(t\right)\right)-\left(d+\lambda \right)R\left(t\right)+v_{1}S\left(t\right)\right]\hfill \end{array}\end{array}$$ (30)

where ${\lambda }_S,{\lambda }_E,{\lambda }_{I_1}$, ${\lambda }_{I_2}$ and λ_R are the adjoint variables. We have to prove the necessary conditions for the optimality of the fractional system (24). For the optimal control v(t), that minimizes the performance index

$$\mathrm{Y}\left(v\right)=\underset{0}{\overset{\tau }{\int }}\mathcal{L}\left(t,\pi ,v\right)dt$$ (31)

subjected to the dynamical constraints

$${}_0^C{D}_t^{\kappa }\pi \left(t\right)=\omega \left(t,\pi ,v\right)$$ (32)

with initial conditions

$$\pi \left(0\right)={\pi }_0$$ (33)

where π(t) and v(t) are the state and control variables, respectively, $\mathcal{L}$ and ω are differentiable functions, and 0 < κ ≤ 1. We have the following theorem.

Theorem 5.1

If (π, v) is a minimizer of (31) under the dynamic constraint (32) and the boundary condition (33), then there exists a function λ such that the triplet (π, v, λ) satisfies

$$\begin{array}{c}\hfill \{\begin{array}{c}{\displaystyle {}_0^C{D}_t^{\kappa }\pi \left(t\right)=\frac{\partial \mathcal{H}}{\partial \lambda }(t,\pi \left(t\right),v\left(t\right),\lambda \left(t\right))}\hfill \\ {\displaystyle {}_0^C{D}_t^{\kappa }\lambda \left(t\right)=-\frac{\partial \mathcal{H}}{\partial \pi }(t,\pi \left(t\right),v\left(t\right),\lambda \left(t\right))}\hfill \\ {\displaystyle 0=\frac{\partial \mathcal{H}}{\partial v}(t,\pi \left(t\right),v\left(t\right),\lambda \left(t\right))}\hfill \\ {\displaystyle \lambda \left(\tau \right)=0}\hfill \\ {\displaystyle }\hfill \end{array}\end{array}$$ (34)

for the Hamiltonian $\mathcal{H}\left(t,\pi ,v,\lambda \right)=\mathcal{L}\left(t,\pi ,v\right)+{\lambda }^T\omega \left(t,\pi ,v\right)$.

Proof

For the proof of theorem 5.1, readers are suggested to see [7,[35], [36]], where the authors have given the proof in detail. This completes the proof of the theorem 5.1. □

Theorem 5.2

Let $S^{*},E^{*},I_1^{*},I_2^{*}$ and R* be optimal state solutions with associated optimal control variables $v_1^{*},v_2^{*},v_3^{*},v_4^{*}$ for the optimal control problems (24) and (26). Then there exist adjoint variables ${\lambda }_S,{\lambda }_E,{\lambda }_{I_1}$, ${\lambda }_{I_2}$ and λ_R satisfying

$$\begin{array}{c}\hfill \{\begin{array}{c}{\displaystyle {{\lambda }^{\prime }}_S=({\lambda }_S-{\lambda }_E)\left[(1-v_2)({\beta }_1{I}_1+{\beta }_2{I}_2)\right]+({\lambda }_S-{\lambda }_R)v_1+\lambda {\lambda }_S}\hfill \\ {\displaystyle {{\lambda }^{\prime }}_E=-\mathbb{Q}+{\lambda }_E(\lambda +\sigma )-{\lambda }_{I_1}\sigma }\hfill \\ {\displaystyle {{\lambda }^{\prime }}_{I_1}=({\lambda }_S-{\lambda }_E)\left[(1-v_2){\beta }_{1}S\right]+({\lambda }_{I_1}-{\lambda }_R)\rho +({\lambda }_{I_1}-{\lambda }_{I_2})\theta +\lambda {\lambda }_{I_1}+{\lambda }_{I_2}{v}_4}\hfill \\ {\displaystyle {{\lambda }^{\prime }}_{I_2}=({\lambda }_S-{\lambda }_E)\left[(1-v_2){\beta }_{2}S\right]+({\lambda }_{I_2}-{\lambda }_R)\rho +\lambda {\lambda }_{I_2}+{\lambda }_{I_2}{v}_3}\hfill \\ {\displaystyle {{\lambda }^{\prime }}_R={\lambda }_R(d-\lambda )}\hfill \end{array}\end{array}$$ (35)

with transversality conditions or boundary conditions

$${\lambda }_S\left(\tau \right)=0,{\lambda }_E\left(\tau \right)=0,{\lambda }_{I_1}\left(\tau \right)=0,{\lambda }_{I_2}\left(\tau \right)=0\text{and}{\lambda }_R\left(\tau \right)=0$$

Furthermore, the control functions $v_1^{*},v_2^{*},v_3^{*}$ and $v_4^{*}$ are given by

$$\begin{array}{c}\hfill \{\begin{array}{c}{\displaystyle v_1^{*}=\min (1,\max (0,\frac{({\lambda }_S-{\lambda }_R)S\left(t\right)}{-{\mathrm{p}}_1}))}\hfill \\ {\displaystyle v_2^{*}=\min (1,\max (0,\frac{({\lambda }_E-{\lambda }_S)({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2(t)S\left(t\right)}{-{\mathrm{p}}_2}))}\hfill \\ {\displaystyle v_3^{*}=\min (1,\max (0,\frac{{\lambda }_{I_2}{I}_2\left(t\right)}{-{\mathrm{p}}_3}))}\hfill \\ {\displaystyle v_4^{*}=\min (1,\max (0,\frac{{\lambda }_{I_1}{I}_1\left(t\right)}{-{\mathrm{p}}_4}))}\hfill \end{array}.\end{array}$$ (36)

Proof

The adjoint system (35) i.e., ${\lambda }_S^{\prime }$, ${\lambda }_E^{\prime }$, ${\lambda }_{I_1}^{\prime }$,${\lambda }_{I_2}^{\prime }$ and ${\lambda }_R^{\prime }$ are obtained from the Hamiltonian $\mathcal{H}$ as

• ${\displaystyle -\frac{d{\lambda }_S}{dt}=\frac{\partial \mathcal{H}}{\partial S}}$, ${\displaystyle -\frac{d{\lambda }_E}{dt}=\frac{\partial \mathcal{H}}{\partial E}}$, ${\displaystyle -\frac{d{\lambda }_{I_1}}{dt}=\frac{\partial \mathcal{H}}{\partial I_1}}$, ${\displaystyle -\frac{d{\lambda }_{I_2}}{dt}=\frac{\partial \mathcal{H}}{\partial I_2}}$, ${\displaystyle -\frac{d{\lambda }_R}{dt}=\frac{\partial \mathcal{H}}{\partial R}}$,

with zero final time conditions (transversality) conditions

$${\lambda }_S\left(\tau \right)=0,{\lambda }_E\left(\tau \right)=0,{\lambda }_{I_1}\left(\tau \right)=0,{\lambda }_{I_2}\left(\tau \right)=0\text{and}{\lambda }_R\left(\tau \right)=0$$

and the characterization of the fractional optimal control given by (36) is obtained by solving the equations

• ${\displaystyle \frac{\partial \mathcal{H}}{\partial v_1}=0}$, ${\displaystyle \frac{\partial \mathcal{H}}{\partial v_2}=0}$, ${\displaystyle \frac{\partial \mathcal{H}}{\partial v_3}=0}$, and ${\displaystyle \frac{\partial \mathcal{H}}{\partial v_4}=0}$

on the interior of the control set and using the property of the control space V.

This completes the proof of the theorem 5.2. □

6. Numerical scheme for the solution

In this section numerical solution for the proposed fractional order SEI₁I₂R epidemic model (9) is presented. Because no analytical solution to the nonlinear fractional system (9) is available, we use the technique so-called generalized Adams-Bashforth-Moulton method [3,35,37] to obtain the numerical solution of the system (9). In this algorithm, we derive the predictor-corrector scheme for obtaining the numerical solution of the nonlinear FDEs. To provide the estimated solution by means of this algorithm, consider the subsequent nonlinear fractional differential equation [3,35,37]

$${}_0{D}_t^{\kappa }\psi \left(t\right)=f\left(t,\psi \left(t\right)\right),0\le t\le T$$ (37)

with the following initial conditions

$${\psi }^{\left(j\right)}\left(0\right)={\psi }_0^j,j=0,1,2,...,\left[\kappa \right]-1,$$ (38)

Now, with operating by the fractional integral operator on the equation (37), we can obtain on the solution ψ(t) by solving the following equation:

$$\psi \left(t\right)=\sum _{j=0}^{\left[\kappa \right]-1}\frac{{\psi }_0^j}{j!}{t}^j+\frac{1}{\Gamma \left(\kappa \right)}\underset{0}{\overset{t}{\int }}{(t-\tau )}^{\kappa -1}f\left(\tau ,\psi \left(\tau \right)\right)d\tau ,$$ (39)

this equation (39) is equivalent to the Volterra integral equation.

Diethelm et al. [70], [71], [72] used the predictor-corrector scheme based on the Adams-Bashfort-Moulton algorithm to integrate (39). Setting $h=\frac{T}{N},t_n=nh$ and $n=0,1,2,...,N\in Z^{+},$ the equation (39) can be discretized as follows:

$${\psi }_h\left(t_{n+1}\right)=\sum _{j=0}^{\left[\kappa \right]-1}\frac{{\psi }_0^j}{j!}{t}_{n+1}^j+\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}f\left(t_{n+1},{\psi }_h^p\left(t_{n+1}\right)\right)+\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}\sum _{q=0}^n{a}_{q,n+1}f\left(t_q,{\psi }_h\left(t_q\right)\right)$$ (40)

where

$$\begin{array}{c}\hfill a_{q,n+1}=\{\begin{array}{c}{\displaystyle n^{\kappa +1}-(n-\kappa ){(n+1)}^{\kappa },\mathit{if}q=0,}\hfill \\ {\displaystyle {(n-q+2)}^{\kappa +1}+{(n-q)}^{\kappa +1}-2{(n-q+1)}^{\kappa +1},\mathit{if}0<q\le n,}\hfill \\ {\displaystyle 1,\mathit{if}q=n+1}\hfill \end{array}.\end{array}$$ (41)

and the predicted value ${\psi }_h^p\left(t_{n+1}\right)$ is determined by

$${\psi }_h^p\left(t_{n+1}\right)=\sum _{j=0}^{\left[\kappa \right]-1}\frac{{\psi }_0^j}{j!}{t}_{n+1}^j+\frac{1}{\Gamma \left(\kappa \right)}\sum _{q=0}^n{b}_{q,n+1}f\left(t_q,{\psi }_h\left(t_q\right)\right)$$

with

$$b_{q,n+1}=\frac{h^{\kappa }}{\kappa }\left({(n+1-q)}^{\kappa }-{(n-q)}^{\kappa }\right).$$ (42)

The error estimate is

$$\underset{q=0,1,2,...,m}{max}\left|\psi \left(t_q\right)-{\psi }_h\left(t_q\right)\right|=o\left(h^p\right),$$

in which $p=\min (2,1+\kappa )$.

6.1. Application of Adams-Bashforth-Moulton method to the proposed model

In this subsection, we solve numerically the nonlinear fractional SEI₁I₂R epidemic model using the proposed method. In view of the generalized Adams-Bashforth-Moulton method, the numerical scheme for the proposed model (9) is given in the following form [73], [74], [75], [76], [77]

$$\begin{array}{ccc}\hfill S_h\left(t_{n+1}\right)& =& S_0+\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}{f}_S\left(t_{n+1},S_h^p\left(t_{n+1}\right),E_h^p\left(t_{n+1}\right),I_{1,h}^p\left(t_{n+1}\right),I_{2,h}^p\left(t_{n+1}\right),R_h^p\left(t_{n+1}\right)\right)\hfill \\ & & +\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}\sum _{q=0}^n{a}_{q,n+1}{f}_S\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill E_h\left(t_{n+1}\right)& =& E_0+\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}{f}_E\left(t_{n+1},S_h^p\left(t_{n+1}\right),E_h^p\left(t_{n+1}\right),I_{1,h}^p\left(t_{n+1}\right),I_{2,h}^p\left(t_{n+1}\right),R_h^p\left(t_{n+1}\right)\right)\hfill \\ & & +\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}\sum _{q=0}^n{a}_{q,n+1}{f}_E\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill I_{1,h}\left(t_{n+1}\right)& =& I_{1,0}+\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}{f}_{I_1}\left(t_{n+1},S_h^p\left(t_{n+1}\right),E_h^p\left(t_{n+1}\right),I_{1,h}^p\left(t_{n+1}\right),I_{2,h}^p\left(t_{n+1}\right),R_h^p\left(t_{n+1}\right)\right)\hfill \\ & & +\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}\sum _{q=0}^n{a}_{q,n+1}{f}_{I_1}\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill I_{2,h}\left(t_{n+1}\right)& =& I_{2,0}+\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}{f}_{I_2}\left(t_{n+1},S_h^p\left(t_{n+1}\right),E_h^p\left(t_{n+1}\right),I_{1,h}^p\left(t_{n+1}\right),I_{2,h}^p\left(t_{n+1}\right),R_h^p\left(t_{n+1}\right)\right)\hfill \\ & & +\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}\sum _{q=0}^n{a}_{q,n+1}{f}_{I_2}\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill R_h\left(t_{n+1}\right)& =& R_0+\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}{f}_R\left(t_{n+1},S_h^p\left(t_{n+1}\right),E_h^p\left(t_{n+1}\right),I_{1,h}^p\left(t_{n+1}\right),I_{2,h}^p\left(t_{n+1}\right),R_h^p\left(t_{n+1}\right)\right)\hfill \\ & & +\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}\sum _{q=0}^n{a}_{q,n+1}{f}_R\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),\hfill \end{array}$$

where

$$S_h^p\left(t_{n+1}\right)=S_0+\frac{1}{\Gamma \left(\kappa \right)}\sum _{q=0}^n{b}_{q,n+1}{f}_S\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),$$

$$E_h^p\left(t_{n+1}\right)=E_0+\frac{1}{\Gamma \left(\kappa \right)}\sum _{q=0}^n{b}_{q,n+1}{f}_E\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),$$

$$I_{1,h}^p\left(t_{n+1}\right)=I_{1,0}+\frac{1}{\Gamma \left(\kappa \right)}\sum _{q=0}^n{b}_{q,n+1}{f}_{I_1}\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),$$

$$I_{2,h}^p\left(t_{n+1}\right)=I_{2,0}+\frac{1}{\Gamma \left(\kappa \right)}\sum _{q=0}^n{b}_{q,n+1}{f}_{I_2}\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),$$

$$R_h^p\left(t_{n+1}\right)=R_0+\frac{1}{\Gamma \left(\kappa \right)}\sum _{q=0}^n{b}_{q,n+1}{f}_R\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right).$$

Further, the quantities

$$f_S\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),f_E\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),$$

$$f_{I_1}\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),f_{I_2}\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right),$$

and f_R(t_q, S_h(t_q), E_h(t_q), I _{1, h}(t_q), I _{2, h}(t_q), R_h(t_q)), are computed from the following functions,

$$f_S\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right)=\Lambda -S\left(t\right)\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)-\lambda S\left(t\right)$$ (43)

$$f_E\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right)=S\left(t\right)\left({\beta }_1{I}_1\left(t\right)+{\beta }_2{I}_2\left(t\right)\right)-\left(\lambda +\sigma \right)E\left(t\right)$$ (44)

$$f_{I_1}\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right)=\sigma E\left(t\right)-\left(\rho +\lambda +\theta \right)I_1\left(t\right)$$ (45)

$$f_{I_2}\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right)=\theta I_1\left(t\right)-\left(\lambda +\rho \right)I_2\left(t\right)$$ (46)

$$f_R\left(t_q,S_h\left(t_q\right),E_h\left(t_q\right),I_{1,h}\left(t_q\right),I_{2,h}\left(t_q\right),R_h\left(t_q\right)\right)=\rho \left(I_1\left(t\right)+I_2\left(t\right)\right)-\left(d+\lambda \right)R\left(t\right)$$ (47)

In addition, the quantities

$$f_S\left(t_{n+1},S_h^p\left(t_{n+1}\right),E_h^p\left(t_{n+1}\right),I_{1,h}^p\left(t_{n+1}\right),I_{2,h}^p\left(t_{n+1}\right),R_h^p\left(t_{n+1}\right)\right),$$

$$f_E\left(t_{n+1},S_h^p\left(t_{n+1}\right),E_h^p\left(t_{n+1}\right),I_{1,h}^p\left(t_{n+1}\right),I_{2,h}^p\left(t_{n+1}\right),R_h^p\left(t_{n+1}\right)\right),$$

$$f_{I_1}\left(t_{n+1},S_h^p\left(t_{n+1}\right),E_h^p\left(t_{n+1}\right),I_{1,h}^p\left(t_{n+1}\right),I_{2,h}^p\left(t_{n+1}\right),R_h^p\left(t_{n+1}\right)\right),$$

$$f_{I_2}\left(t_{n+1},S_h^p\left(t_{n+1}\right),E_h^p\left(t_{n+1}\right),I_{1,h}^p\left(t_{n+1}\right),I_{2,h}^p\left(t_{n+1}\right),R_h^p\left(t_{n+1}\right)\right),$$

$$f_R\left(t_{n+1},S_h^p\left(t_{n+1}\right),E_h^p\left(t_{n+1}\right),I_{1,h}^p\left(t_{n+1}\right),I_{2,h}^p\left(t_{n+1}\right),R_h^p\left(t_{n+1}\right)\right),$$

are computed from equations (43)-(47) respectively, at the points $t_{n+1},n=1,2,3,...,m.$

For the fractional optimal control problem (24) discussed in section 5, similar procedure is followed for the numerical results. Therefore

$${\pi }_h\left(t_{n+1}\right)={\pi }_0+\frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}\left[{\omega }_{\pi }\left(t_{n+1},{\pi }_h^p\left(t_{n+1}\right),v_h\left(t_{n+1}\right)\right)+\sum _{q=0}^n{a}_{q,n+1}{\omega }_{\pi }\left(t_q,{\pi }_h\left(t_q\right),v_h\left(t_q\right)\right)\right]$$

where

$${\pi }_h^p\left(t_{n+1}\right)={\pi }_0+\frac{h^{\kappa }}{\Gamma \left(\kappa \right)}\sum _{q=0}^n{b}_{q,n+1}{\omega }_{\pi }\left(t_q,{\pi }_q,v_q\right)$$

with $\pi =S,E,I_1,I_2,R$ and the control v.

Similarly, for the adjoint system we have

$$\begin{array}{ccc}\hfill {\lambda }_h\left(t_{n+1}\right)& =& \frac{h^{\kappa }}{\Gamma \left(\kappa +2\right)}[\frac{\partial \mathcal{H}}{\partial \pi }\left(t_{n+1},{\pi }_h\left(t_{n+1}\right),v_h\left(t_{n+1}\right),{\lambda }_h^p\left(t_{n+1}\right)\right)\hfill \\ & & +\sum _{q=0}^n{a}_{q,n+1}\frac{\partial \mathcal{H}}{\partial \pi }(t_q,{\pi }_h\left(t_q\right),v_h\left(t_q\right),{\lambda }_h\left(t_q\right))]\hfill \end{array}$$

where

${\lambda }_h^p\left(t_{n+1}\right)=\frac{h^{\kappa }}{\Gamma \left(\kappa \right)}\sum _{q=0}^n{b}_{q,n+1}\frac{\partial \mathcal{H}}{\partial \pi }\left(t_q,{\pi }_q,v_q,{\lambda }_q\right)$.

The coefficients $a_{q,n+1}$, $b_{q,n+1}$ are given by equations (41) and (42) respectively.

7. Numerical results and discussion

In order to justify our theoretical findings, we introduced in this section some numerical experiments obtained for different instances of fractional power κ for the HIV epidemic model without control (9) and with control (24) along with adjoint variable systems and the control strategies. We present the numerical results for the model (9) when all control measures are absent and also to examine the role of fractional order κ on the HIV disease spread. Then, we simulate the fractional optimal control of the model and investigate the effect of the controls introduced in the model on the spread of epidemics. We use the generalized Adams-Bashforth-Moulton method for the simulation of both the systems and use the values of parameters described in Table 1 .

Table 1.

Parameters and variables with their values for fractional order SEI₁I₂R epidemic model [3,5,15,18,[59], [60]].

Parameters and functions	Meaning	Values
S(t)	Susceptible individuals at time t	Variable
E(t)	Exposed individuals at time t	Variable
I1(t)	Unaware infected individuals at time t	Variable
I2(t)	Aware infected individuals at time t	Variable
R(t)	Recovered individuals at time t	Variable
Λ	Recruitment rate	0.32
β1	Unaware infection rate	0.00009
β2	Aware infection rate	0.000027
λ	Natural death rate	0.2
σ	Infected class rate	0.01
θ	Awareness rate	0.015
ρ	Recovery rate	0.5
d	AIDs related death rate	0.1
S0	Initially susceptible individuals	200
E0	Initially exposed individuals	0.01
I1, 0	Initially unaware infected individuals	0.02
I2, 0	Initially aware infected individuals	0.01
R0	Initially recovered individuals	0.0

7.1. Numerical simulation without control measures

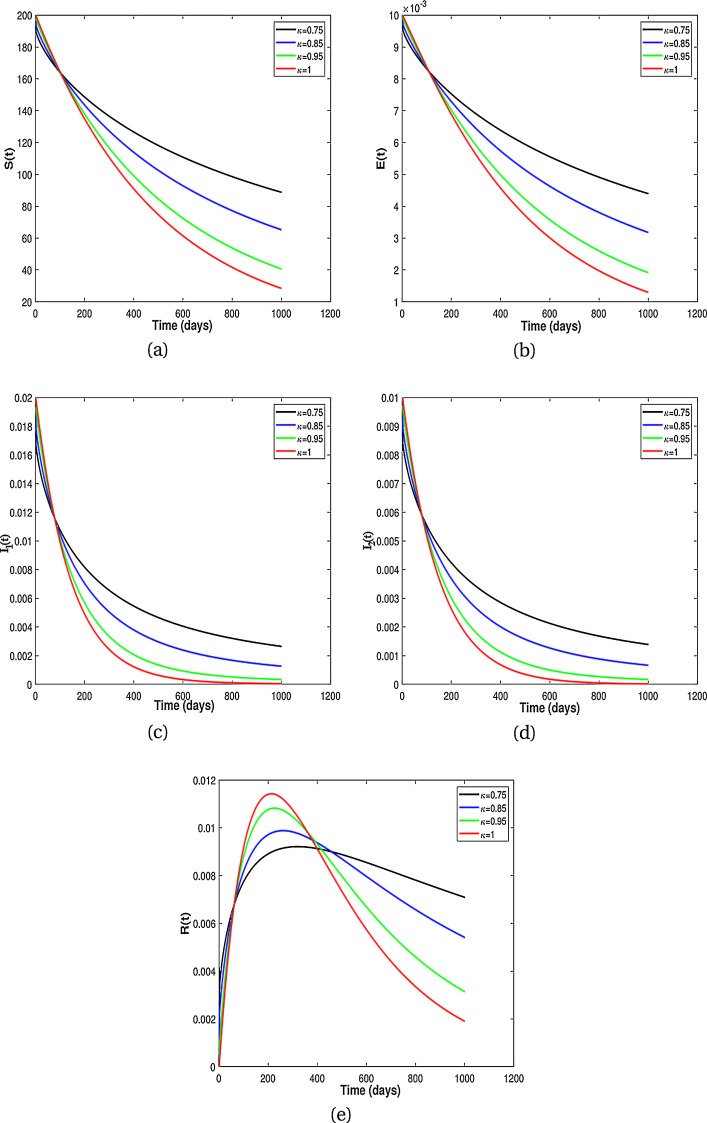
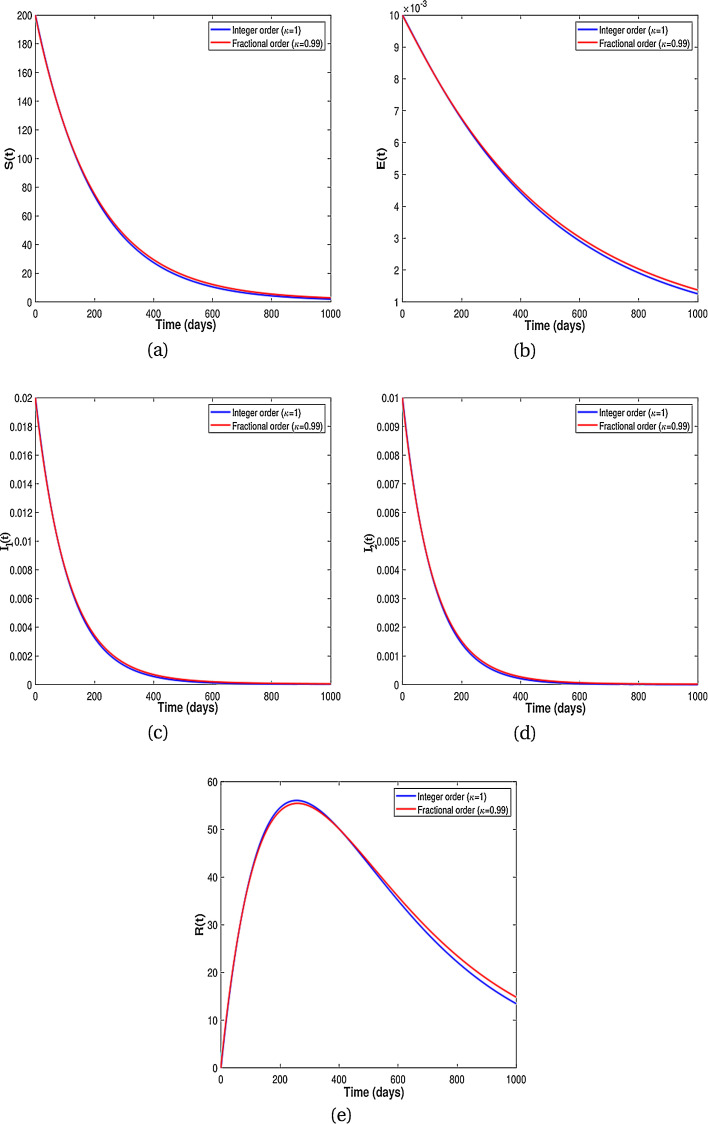
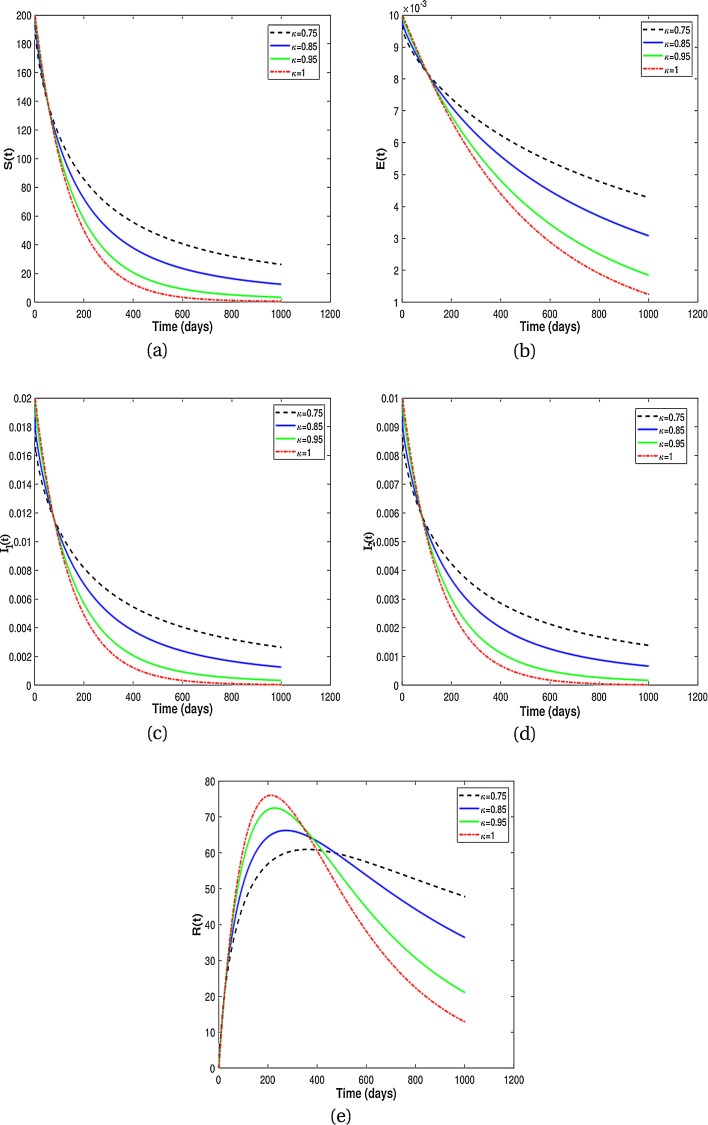
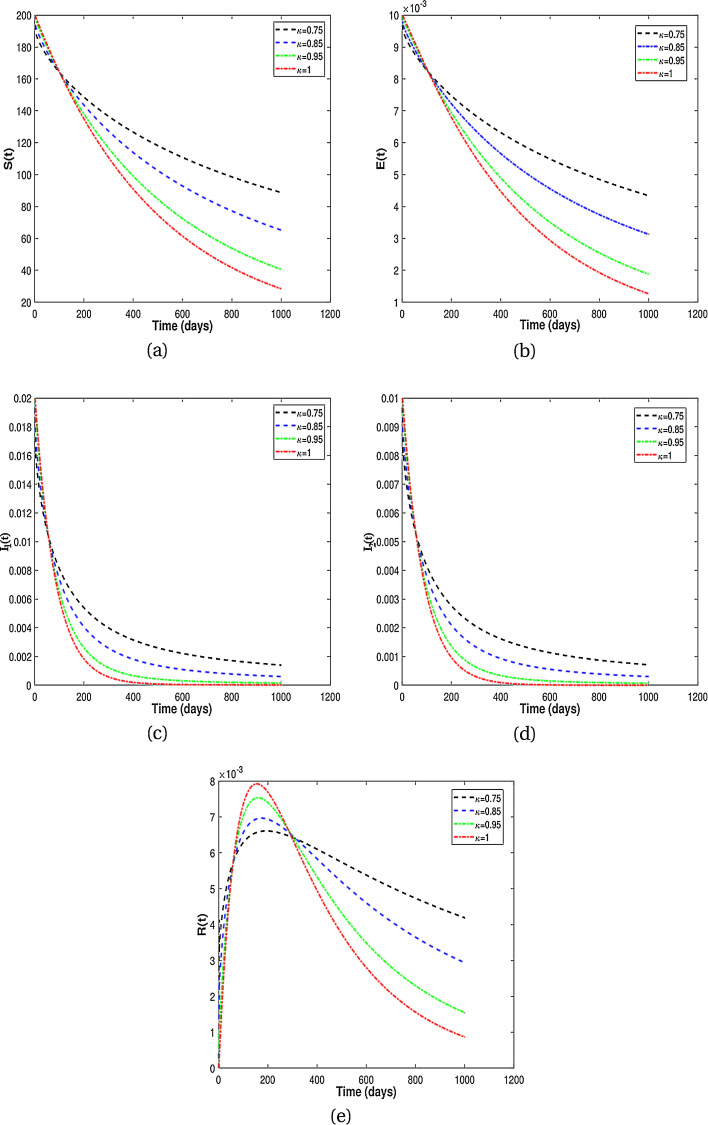
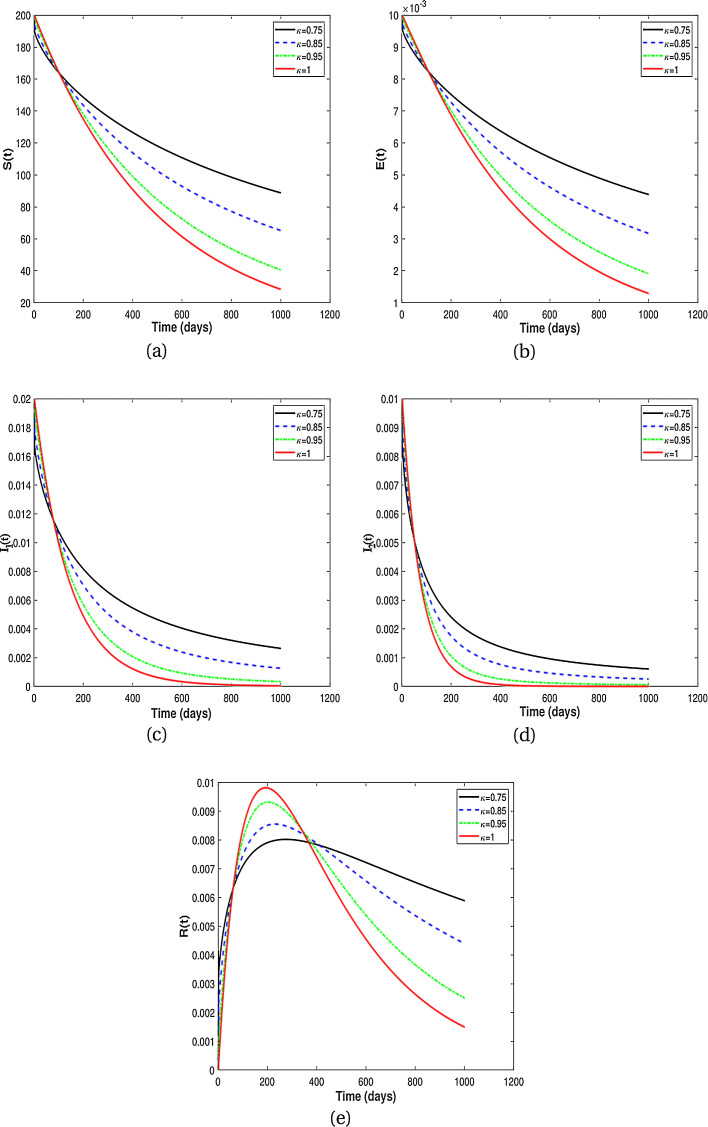
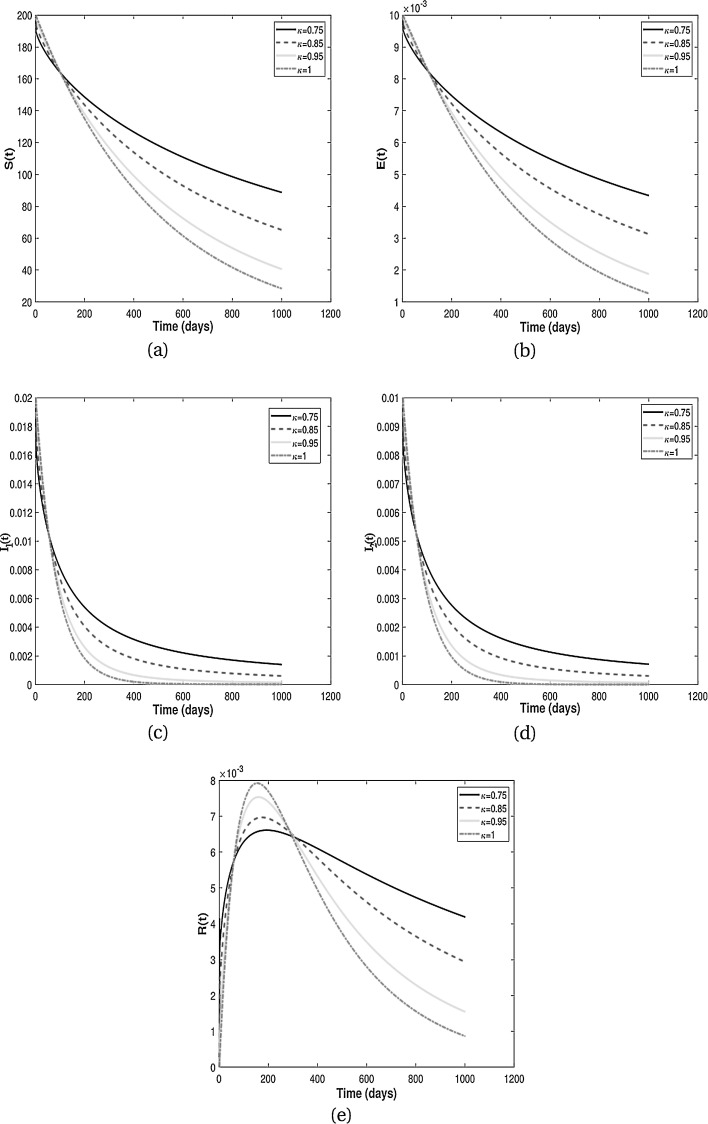
In this subsection, we present numerical results for fractional system (9) and allow the values of κ to varies from $k=0.75$ to $k=1$ as seen in the Fig. 2 . It is clear from the Fig. 2 that fractional order has significant effect on dynamic behavior of all the components. We observe that when the derivative order κ is reduced from 1, the memory effect of the system increases, and therefore the infection grows slowly and the number of HIV-infected population and AIDS people increases for a long time. Also, undiagnosed HIV-infected population in some societies refuse to perform HIV test for reasons such as stigma and fear of identification due to lack of knowledge about the disease. This results in a delay in identification of HIV-infected individuals, an increase in the undiagnosed HIV-infected population, fast progress of AIDS and an increase in people diagnosed with AIDS. On the other hand, the experience or knowledge of individuals about the disease causes susceptible and exposed individuals to take different precautions, such as behavioral change, vaccination, treatment and condom use, against infection transmission. This leads to a slow growth of infection among the population. Therefore, from the numerical results in Fig. 2, we conclude that the derivative order κ (0.75 ≤ κ ≤ 1) can play the role of precautionary measures against infection transmission, treatment of infection and delay in accepting HIV test.

Fig. 2.

Numerical results for different fractional order κ.

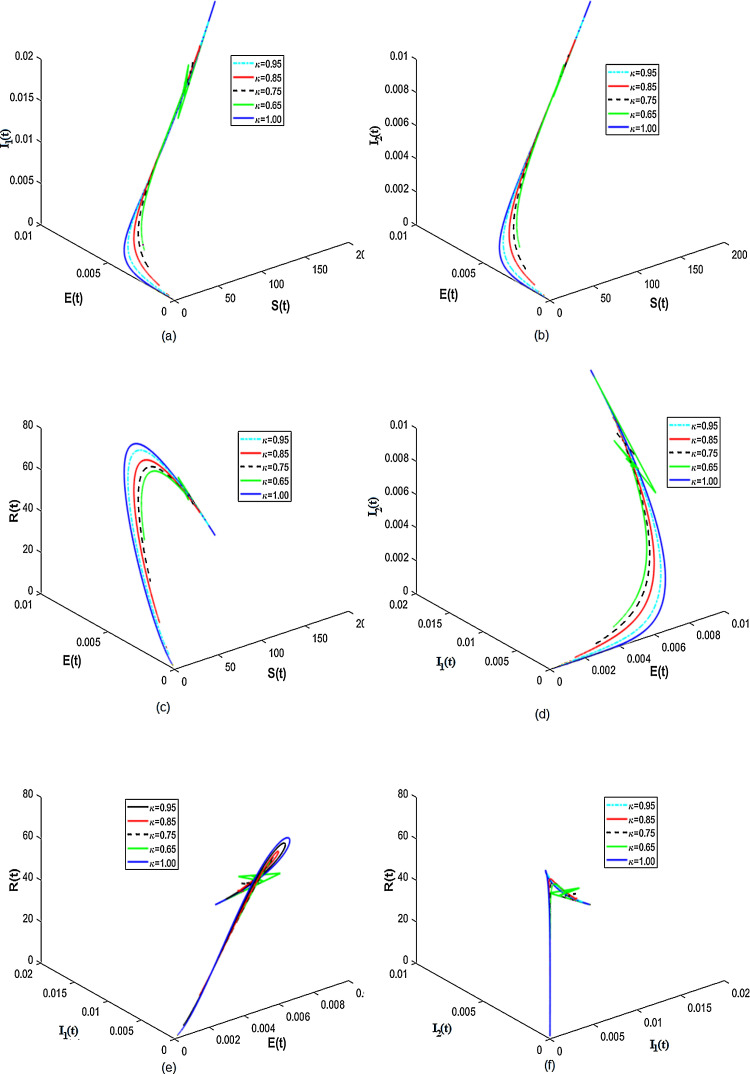
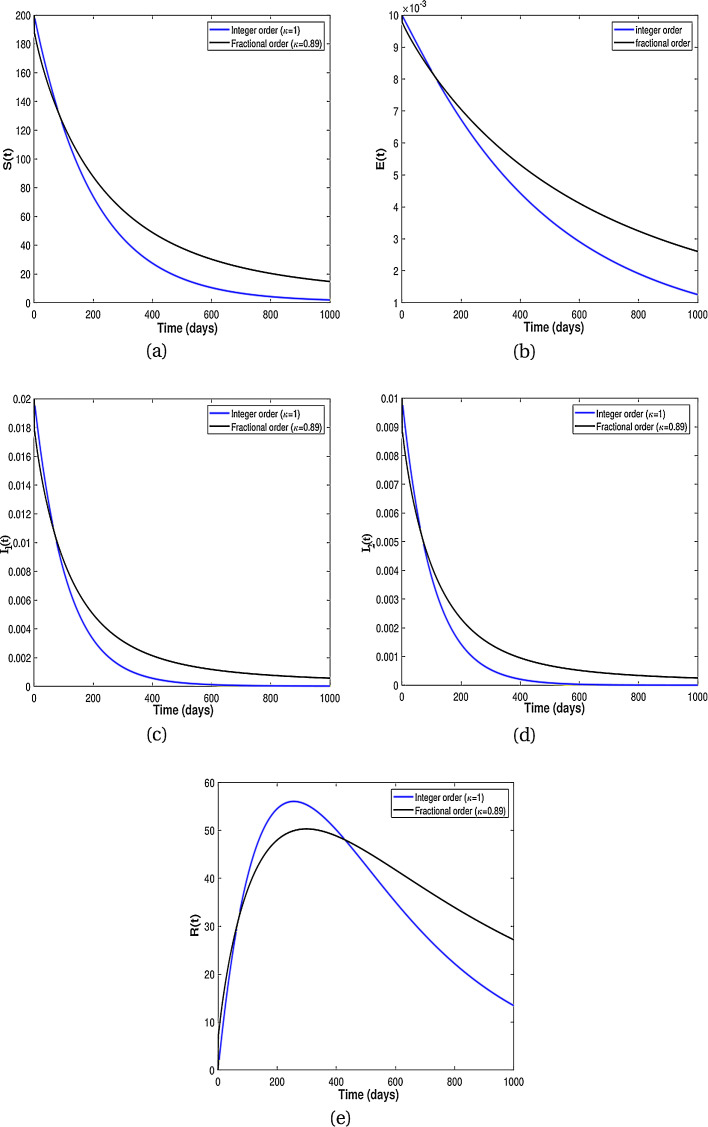
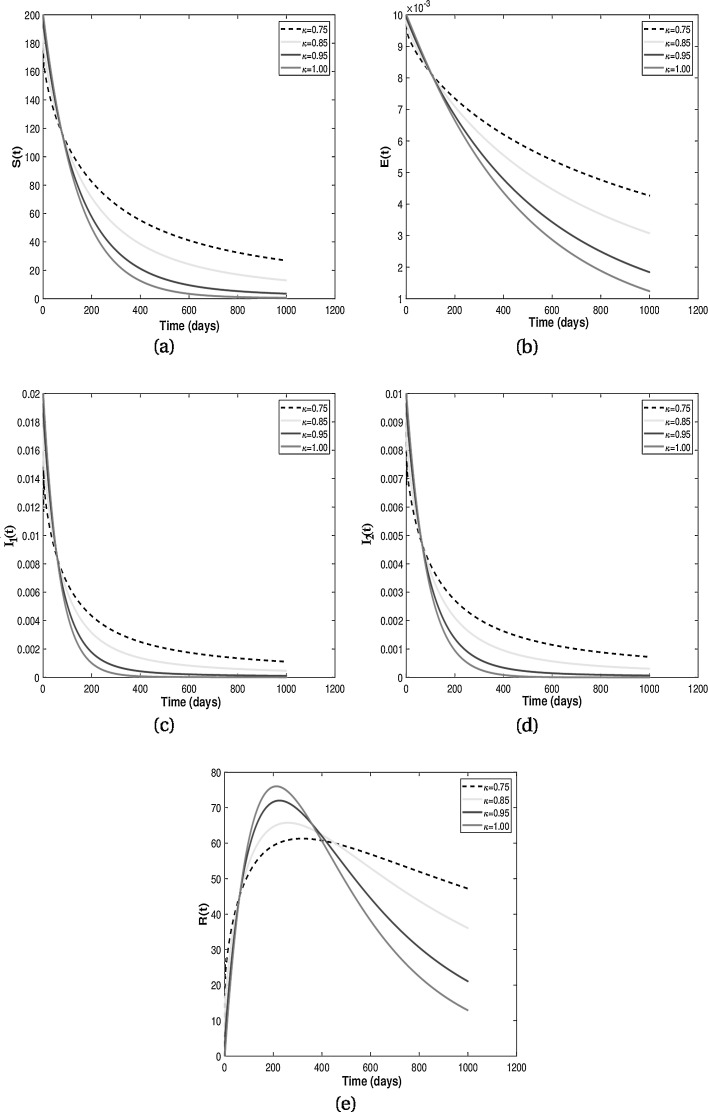
Existence of attractors for some fractional order κ for different population groups are given in Fig. 3 . Thus, the results from Fig. 3 shows that there is tendency of each population class to exist and enter into permanence with time. Numerical results for the difference of integer-order and fractional order are given in Fig. 4, Fig. 5 . It is clearly visible from Fig. 4, Fig. 5 that the differential equations with fractional order derivative have rich dynamics and describe biological systems better than traditional integer-order models.

Fig. 3.

Numerical results showing the existence of attractors for different values of κ.

Fig. 4.

Numerical results showing comparison between the classical model (8) and the fractional dynamics (9) with $\kappa =0.89$.

Fig. 5.

Numerical results showing comparison between the classical model (8) and the fractional dynamics (9) with $\kappa =0.99$.

From the above discussion and numerical results in Fig. 2, Fig. 3, Fig. 4, Fig. 5, we conclude that the derivative order κ can play the role of experience or knowledge of individuals about the past of the disease. Therefore, the numerical results confirm that differential equations with fractional order derivative have rich dynamics and describe biological systems better than traditional integer order models. As a result, our numerical results are more logical than the results of other articles on the modeling of the HIV/AIDS epidemic and other models with integer-order derivative due to the presence of the fractional derivative order κ (0.75 < κ ≤ 1).

Now, we investigate the effect of the control measures introduced in the model on the spread of the epidemic. We consider the following strategies and examine the corresponding numerical results.

7.2. Numerical simulation with control measures

In this subsection, we present the numerical results for the model (24) when all control measures are present. The results are obtained in different ways by applying control strategies in the following five ways.

Strategy-1. Using behavioral change control and condom use control (v ₁ ≠ 0, v ₂ ≠ 0) and $({\mathit{v}}_3={\mathit{v}}_4=0)$ .

In the first control strategy, we set the control measures $v_3=0,$ $v_4=0$ and active the control measures $v_1=0.5,$ $v_2=0.5$ namely the behavioral change for susceptible individuals and condom use for the exposed individuals which is shown in Fig. 6 , for different values of fractional order κ. Analysis of control strategy-1 predicts that susceptible and exposed individuals greatly decrease after implementing control measure v ₁, v ₂. In Fig. 6, we observe that this control strategy results in a significant decrease in the number of undiagnosed HIV-infected population and AIDS people for a long time compared with the case without control. Fig. 6 shows that, by applying the strategy-1, the value of ${\mathcal{R}}_0$ will be less than 1 for more time when κ is reduced from 1. This means that by decreasing κ from 1, we can control the spread of disease over a longer period of time. Therefore, the presence of the fractional derivative order κ in the model increases the use of condom control and behavioural control in the population.

Fig. 6.

Numerical results showing the effect of control measures $v_1=0.5,$$v_2=0.5$ and $v_3=v_4=0$ on the dynamics (9) for different fractional order κ.

The control v ₁ is proportion of the susceptible individuals who change their sexual habits per unit time. The class R, the removed class, represents the number of people who have greatly changed their sexual habits such that they cannot easily be infected through sexual contact. People in the class R take on safe habits and keep these habits in the rest of their lives. The importance of class R is that it emphasizes the need for prevention for a disease like HIV that has no treatment. Therefore, increasing the members of this class plays an important role in controlling the spread of disease.

Strategy-2. Using only condom use control $\left({\mathit{v}}_2\ne 0\mathit{and}{\mathit{v}}_1={\mathit{v}}_3={\mathit{v}}_4=0\right)$ .

In the second control strategy, we set the control measures $v_1=0,v_3=0,$ $v_4=0$ and active the control measure $v_2=0.5$ namely the condom use for the exposed individuals which is shown in Fig. 7 , for different values of fractional order κ. Analysis of control strategy-2 predicts that exposed individuals greatly decrease after implementing control measure v ₂. The results in Fig. 7, further show that condom use is the main control measure which can be helpful in controlling the disease more properly. This is because the control is applied to exposed class which is the main source from which the virus can transmit and spread due to the fact that this class is easily available for virus during their sexual contact with infected female sex workers.

Fig. 7.

Numerical results showing the effect of control measure $v_2=0.5$ and $v_1=v_3=v_4=0$ on the dynamics (9) for different fractional order κ.

Strategy-3. Using only treatment control $\left({\mathit{v}}_3\ne 0\mathit{and}{\mathit{v}}_1={\mathit{v}}_2={\mathit{v}}_4=0\right)$ .

In the third control strategy, we set the control measures $v_1=0,v_2=0,$ $v_4=0$ and active the control measure $v_3=0.7$ namely the efficiency of treatment given to the aware infected individuals which is shown in Fig. 8 , for different values of fractional order κ. Analysis of control strategy-3 predicts that infected individuals greatly decreases after implementing control measure v ₃. This is due to the fact that treatment of diagnosed HIV-infected population results in an increase in the level of CD4⁺ T-cells of this class. Therefore, this strategy prolongs the lifespan of HIV-infected patients and delays the onset of AIDS. Fig. 8 shows that differential equations with fractional order derivative have rich dynamics and describe biological systems better than traditional integer-order models.

Fig. 8.

Numerical results showing the effect of control measure $v_3=0.7$ and $v_1=v_2=v_4=0$ on the dynamics (9) for different fractional order κ.

Strategy-4. Using treatment control and awareness control $\left({\mathit{v}}_1={\mathit{v}}_2=0\mathit{and}{\mathit{v}}_3\ne 0,{\mathit{v}}_4\ne 0\right)$ .

In the fourth control strategy, we set the control measures $v_1=0,v_2=0$ and active the control measures $v_3=0.5$, $v_4=0.5$ namely the efficiency of treatment given to the aware infected individuals and the awareness source for unaware infected individuals which is shown in Fig. 9, for different values of fractional order κ. Analysis of control strategy-4 predicts that infected individuals greatly decreases after implementing control measures v ₃ and v ₄. In Fig. 9 , we observe that this control strategy results in a significant decrease in the number of aware infected HIV people and unware infected people compared with the case without control.

Fig. 9.

Numerical results showing the effect of control measure $v_1=v_2=0$ and $v_3=v_4=0.5$ on the dynamics (9) for different fractional order κ.

Strategy-5. Using all controls (v ₁ ≠ 0, v ₂ ≠ 0, v ₃ ≠ 0, v ₄ ≠ 0).

In last control strategy, we activate all the control measures $v_1=0.5,v_2=0.5,v_4=0.5$ and $v_4=0.8$ namely the behavioral change for susceptible individuals, condom use for exposed individuals, efficiency of treatment given to the aware infected individuals and the awareness source for unaware infected individuals which is shown in Fig. 10 , for different values of fractional order κ. Analysis of control strategy-5 predicts that susceptible individuals and exposed individuals decreases with the control measures v ₁ and v ₂ while infected individuals greatly decrease after implementing control measures v ₃ and v ₄.

Fig. 10.

Numerical results showing the effect of all control measures $v_1=0.5,v_2=0.5,$$v_3=0.5$and $v_4=0.8$ on the dynamics (9) for different fractional order κ.

By adding the behavioral change control v ₁ or condom use control v ₂ to the ART treatment control v ₃, we see from Fig. 6, Fig. 7, Fig. 8, Fig. 9, that the strategies 1-4 result in a decrease in the HIV infected population and AIDS people compared with the case without control. With implementing all the control efforts, we observe that the strategy-5 results in a significant decrease in the HIV-infected population and AIDS people compared with the case without control. With comparison of the strategies, we see that the strategy-5 is better than the other strategies in control and reduction of the spread of HIV/AIDS epidemic. Therefore, by applying the strategy-5, we can increase the life time and the quality of life for those living with HIV and decrease significantly the number of HIV-infected population and AIDS people.

On the other hand, in human societies, the process of evolution and control of the epidemic is associated with memory. When a disease spreads in a society, the experience or knowledge of individuals about the past of the disease helps susceptible individuals to take different precautions, such as behavioural change, treatment, awareness and condom use against infection transmission. Also, the experience or knowledge can lead to the screening measures of entry and exit between different groups.

It is noticeable from Fig. 10 that due to the memory property of fractional derivatives, the derivative order κ affects the values of the controls. We see that the maximum levels of the controls are reduced when κ limits to 1. On the other hand, the memory effect characterized by fractional derivative is reduced when κ limits to 1. Therefore, by reducing the memory effect, the maximum levels of the controls are reduced.

8. Conclusion

In the current study, we have introduced a nonlinear SEI₁I₂R fractional order epidemic model for the transmission dynamics of HIV epidemics. The non-negative solution of the model is provided by using the generalized mean value theorem. We obtained the basic reproductive number ${\mathcal{R}}_0$, which perform as a threshold parameter in the disease status. The existence of equilibria and their asymptotical stability results using fractional Routh-Hurwitz stability criterion is discussed. We established and investigated the stability analysis of the fractional order model with respect to the values of ${\mathcal{R}}_0$. The disease-free equilibrium is locally asymptotically stable if ${\mathcal{R}}_0\le 1$. For ${\mathcal{R}}_0>1$, using Theorem 4.3 and Corollary 4.1, we investigated the local stability of the positive endemic equilibrium state Đ*. Meanwhile, global asymptotic stability of the disease-free and endemic equilibrium point is investigated by constructing a suitable Lyapunov functions. Additionally, we investigated the optimal control problem by the application of the optimal control theory. We used the Pontryagin's Minimum Principle to provide the necessary conditions needed for the existence of the optimal solution to the optimal control problem. Furthermore, generalized Adams-Bashforth-Moulton method is applied to obtain a numerical solution of the proposed fractional order SEI₁I₂R epidemic model (9) and the fractional optimal problem (24). The results obtained shown that the Adams-Bashforth-Moulton method is an accurate and effective technique for obtaining the numerical solution of the proposed nonlinear fractional order SEI₁I₂R epidemic model. Lastly, the theoretical results are verified by numerical simulations to measure the efficacy and impact of controls on the transmission of the HIV/AIDS disease. From the numerical simulation, the size of the exposed population is significantly reduced under the controlled conditions. This proposes that if all four control measures v ₁ (behavioral change for susceptibles), v ₂ (condom use by the exposed individuals), v ₃ (strength of treatment for the infected individuals), v ₄ (awareness source among the unaware infectives) are employed for the same period of time and continue for a considerable period of time, the spread of HIV disease through prostitution could be restricted. In this manner, the fractional order optimal control method can progress the value of the necessary control measures. This recommends that personal precautional measures, periodic monitoring by medical professionals and researchers should be done to control the transmission of the HIV disease dynamics.

The recently emerged virus namely novel coronavirus (COVID-19) which has originated from Wuhan the capital city of Hubei providence of mainland China in December 2019 is a major threat to mankind at present in the whole world. Application of fractional order derivatives to model the new outbreak of coronavirus and other trending diseases are left for future research.

CRediT authorship contribution statement

Parvaiz Ahmad Naik: Conceptualization, Formal analysis, Methodology, Writing - original draft. Jian Zu: Writing - review & editing, Funding acquisition, Supervision. Kolade M. Owolabi: Software, Validation, Project administration.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.