Abstract
A statistical framework of model comparison and model validation is essential to resolving the debates over concatenation and coalescent models in phylogenomic data analysis. A set of statistical tests are here applied and developed to evaluate and compare the adequacy of substitution, concatenation, and multispecies coalescent (MSC) models across 47 phylogenomic data sets collected across tree of life. Tests for substitution models and the concatenation assumption of topologically congruent gene trees suggest that a poor fit of substitution models, rejected by 44% of loci, and concatenation models, rejected by 38% of loci, is widespread. Logistic regression shows that the proportions of GC content and informative sites are both negatively correlated with the fit of substitution models across loci. Moreover, a substantial violation of the concatenation assumption of congruent gene trees is consistently observed across six major groups (birds, mammals, fish, insects, reptiles, and others, including other invertebrates). In contrast, among those loci adequately described by a given substitution model, the proportion of loci rejecting the MSC model is 11%, significantly lower than those rejecting the substitution and concatenation models. Although conducted on reduced data sets due to computational constraints, Bayesian model validation and comparison both strongly favor the MSC over concatenation across all data sets; the concatenation assumption of congruent gene trees rarely holds for phylogenomic data sets with more than 10 loci. Thus, for large phylogenomic data sets, model comparisons are expected to consistently and more strongly favor the coalescent model over the concatenation model. We also found that loci rejecting the MSC have little effect on species tree estimation. Our study reveals the value of model validation and comparison in phylogenomic data analysis, as well as the need for further improvements of multilocus models and computational tools for phylogenetic inference. [Bayes factor; Bayesian model validation; coalescent prior; congruent gene trees; independent prior; Metazoa; posterior predictive simulation.]
Due to the increasing growth in dimensionality and complexity of multilocus sequence data, accurate phylogenetic inference for understanding the evolutionary history of species faces substantial computational and modeling challenges (Rannala and Yang 2008; Liu et al. 2015a; Edwards 2016). With the assumption of topologically congruent (TC) genealogies across loci, a phylogenetic tree estimated from concatenated sequences is often used as the estimate of the species tree, despite the fact that the concatenation model oversimplifies the complexity inherent in the diversification of species by ignoring many biological phenomena, such as deep coalescence, hybridization, recombination, and gene duplication and loss, that are commonly observed during the history of species (Maddison 1997; Rannala and Yang 2003; Bravo et al. 2019). Since the advent of multilocus sequence data, there has been ongoing effort toward building stochastic models for handling gene tree variation. Given that incomplete lineage sorting (ILS) is likely the most common biological source of gene tree variation (Edwards 2009), some of the earliest efforts included parsimony and Bayesian multispecies coalescent (MSC) models based on a coalescence process running along the lineages of the species tree (Page 1998; Liu and Pearl 2007; Liu 2008; Heled and Drummond 2010). Subsequently, the MSC model has been updated by adding biological parameters, such as gene flow, rate variation among lineages, recombination, and hybridization (Kubatko 2009; Hey 2010; Wang et al. 2014). In other developments, methods have been proposed to ask whether a tree is the best model for a given data set, or whether reticulations in the form of gene flow or lineage merging are more appropriate (see below) (Moret et al. 2004; Jackson et al. 2017; Burbrink and Gehara 2018). Meanwhile, skeptics of the MSC and advocates for simpler models, particularly concatenation models, have raised critical questions about appropriateness of the MSC and argued that observed gene tree variation is often not caused by ILS, but instead by gene tree estimation error (Springer and Gatesy 2016; Scornavacca and Galtier 2017; Richards et al. 2018). The inconsistency of concatenation methods under some regions of tree space in which coalescent methods of tree building are still consistent (Liu et al. 2010) should to many researchers be sufficient evidence to choose coalescent over concatenation methods for species tree inference. However, since the mathematical proofs or simulations for inconsistency of concatenation methods assume that the MSC model is true (Kubatko and Degnan 2007; Roch and Steel 2015), it is important to show empirical evidence for validating and comparing the concatenation and MSC models. Resolution of debates over concatenation and coalescent models requires a statistical framework of model comparison and model validation on a variety of empirical and simulated data.
Model Fit and Model Adequacy in Phylogenomics
Discussions about the necessity or adequacy of MSC models versus concatenation have taken three principle forms. One form involves questioning the phylogenetic signal in data sets designed for application of the MSC. For example, several authors have suggested that gene tree error (whether deriving from alignment artifacts, low signal, or gene tree estimation error), rather than ILS, is responsible for most if not all observed gene tree variation (Gatesy and Springer 2014; Arcila et al. 2017). If demonstrable gene tree variation can be ruled out for a given data set, this logic goes, then concatenation is a reasonable fallback model for analysis. This logic reasonably implies that the simpler model inherent in concatenation is favored, especially when gene tree variation can be shown to be low or negligible. The problem with this logic, however, is that gene tree variation is only one motivation for MSC models. The other, more fundamental, motivation for MSC models is the conditional independence of loci in the genome, wherein recombination and random drift render the topologies, but more often the branch lengths of different loci independent of one another, conditional on the species tree, which necessarily influences the shape of all gene trees in the genome (Edwards 2016). This point leads to the second common argument against MSC models: that violation of MSC model assumptions, such as evidence for recombination within loci or lack of recombination between loci or violations of neutrality, render MSC models poor descriptors of actual data sets, again recommending concatenation or other approaches as more robust alternatives (Gatesy and Springer 2014; Scornavacca and Galtier 2017). Again, however, demonstration of violation of a model’s assumptions does not necessarily imply that model is not a reasonable, or even the best available, description of the data. Indeed, we know of no violation of assumptions of an MSC model that is not also a violation of the concatenation model, especially since the concatenation model is best described as a special case of the MSC model, wherein all gene trees are topologically identical (Liu et al. 2015a).
A third approach to deciding whether MSC, concatenation, or other models might best apply to a given data set is testing for model fit and model adequacy (Brown and Thomson 2018). Only a few papers have explicitly tested the fit and adequacy of the MSC, and, crucially, in doing so, have usually neglected to compare the fit of the major alternative model, concatenation, to that of the MSC. Reid et al. (2014) applied posterior predictive simulation (PPS), a Bayesian modeling approach, to a series of moderately sized data sets and concluded that “a poor fit to the MSC is widely detectable in empirical data”. Although this study was a major advance in our understanding of the MSC as applied to real data sets, we wonder whether the sweeping nature of this conclusion is reasonable and suggest that it may have been overly pessimistic. First, they definitively rejected the fit of the MSC at the level of gene trees for only four out of 25 data sets, and only seven total loci (2.9%), hardly suggesting that poor fit at the level of the coalescent is “widespread”. Reid et al. (2014) also suggest that a large percentage of partitions or loci in data sets, sometimes as high as 50%, violate the MSC; but the largest data set in their analysis consisted of only 20 loci, with 15 out of 25 data sets consisting of less than 10 loci, thereby possibly exaggerating the extent of violations of the MSC. Many of these rejections were based not on a poor fit of coalescent assumptions but on deviations of the loci from assumed substitution models, which is hardly a direct rejection of the MSC itself. In several cases, Reid et al. (2014) were unable to distinguish whether the MSC was a poor fit due to analyses at the level of estimating gene trees and substitution models or at the level of the coalescent model itself. In addition, their use of a 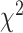 test for comparing the observed site patterns with those expected from the assumed substitution models could not accommodate missing data, making this aspect of their model testing problematic and raising the possibility that different substitution models could improve model fit. Moreover, several of the data sets in their analysis can be reasonably thought of as phylogeographic data sets (e.g., Leache 2009; Walstrom et al. 2012) rather than phylogenomic data sets. Arguably, none of the data sets they analyzed could be called robustly phylogenomic in the modern sense: only five of the data sets interrogated relationships above the level of genus and none of them examined relationships among higher taxa. Jackson et al. (2017) recently applied a novel model fitting algorithm, Phrapl, to a series of multilocus phylogeographic data sets, concluding that a pure isolation model, such as the MSC, is rejected in favor of models including gene flow and other reticulate events. Here, again, however, the data sets analyzed are explicitly termed phylogeographic, and, although the MSC was often applied to these data sets in the original papers, it is unsurprising that this model is a poor fit compared to models that include gene flow. Like all models, the MSC has a particular domain of application, one that we suggest is even wider than that in which concatenation is appropriate, but not so wide as to be applicable to data sets that demonstrably include gene flow or hybridization.
test for comparing the observed site patterns with those expected from the assumed substitution models could not accommodate missing data, making this aspect of their model testing problematic and raising the possibility that different substitution models could improve model fit. Moreover, several of the data sets in their analysis can be reasonably thought of as phylogeographic data sets (e.g., Leache 2009; Walstrom et al. 2012) rather than phylogenomic data sets. Arguably, none of the data sets they analyzed could be called robustly phylogenomic in the modern sense: only five of the data sets interrogated relationships above the level of genus and none of them examined relationships among higher taxa. Jackson et al. (2017) recently applied a novel model fitting algorithm, Phrapl, to a series of multilocus phylogeographic data sets, concluding that a pure isolation model, such as the MSC, is rejected in favor of models including gene flow and other reticulate events. Here, again, however, the data sets analyzed are explicitly termed phylogeographic, and, although the MSC was often applied to these data sets in the original papers, it is unsurprising that this model is a poor fit compared to models that include gene flow. Like all models, the MSC has a particular domain of application, one that we suggest is even wider than that in which concatenation is appropriate, but not so wide as to be applicable to data sets that demonstrably include gene flow or hybridization.
Most arguments in favor of concatenation, such as those summarized above, assert the superiority of concatenation by noting widespread perceived violations of the MSC or lack of demonstrable gene tree variation, and there have only been a few scattered examples of statistical comparisons of model fit and model adequacy between the MSC and concatenation. To our knowledge, only Liu and Pearl (2007) and Edwards et al. (2007) have explicitly compared the fit of MSC and concatenation models to the same data set and asked which is a better fit (model comparison) and whether either model can account for the details of the multilocus data (model adequacy). Tests of model fit and model adequacy have been conspicuously absent from discussions about the relative merits of the MSC versus concatenation, although they have begun to appear in discussions of the relative merits of simple and more elaborate MSC models (Wen et al. 2016; Jackson et al. 2017). Testing whether the MSC or concatenation can adequately describe multilocus data sets, and which model can describe those data better, will go a long way toward addressing concerns about the MSC and toward delimiting its appropriate domain of application.
In this article, we will address several questions regarding the MSC and its application to empirical data sets: (1) Is gene tree variation primarily caused by estimation error? (2) How well do the assumed substitution models fit multilocus sequence data and how does this fit drive the overall fit of the MSC? (3) How well does the MSC model, divorced from shortcomings of the substitution model, fit empirical data? and (4) Which model fits empirical multilocus data sets better, concatenation, or the MSC? Question 1 can be addressed by a likelihood ratio test (LRT), where the null hypothesis is that all loci have the same tree topology (but possibly different branch lengths) versus the alternative hypothesis that allows gene tree variation across loci (testing TC gene trees; Fig. 1). We addressed Question 2 with the same 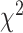 test used by Reid et al. (2014), comparing the observed and expected frequencies of site patterns, but this test cannot be applied to sequences with missing characters. We therefore modified this
test used by Reid et al. (2014), comparing the observed and expected frequencies of site patterns, but this test cannot be applied to sequences with missing characters. We therefore modified this 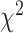 test to handle missing characters (goodness of fit of substitution models; Fig. 1). To evaluate the effect of substitution models on the fit of the MSC, model validation analysis was conducted with different substitution models for the same data sets. Question 3, the adequacy of the MSC, can be addressed using PPS in a Bayesian framework (Reid et al. 2014) implemented in a Bayesian phylogenetic program BEAST (Suchard et al. 2018). Unlike previous studies utilizing sequence data simulated under the MSC model to validate coalescent methods (Kubatko and Degnan 2007), PPS directly evaluates the fit of the MSC model by comparing the posterior gene trees and the gene trees simulated from the MSC (Reid et al. 2014). However, the posterior gene trees generated with a coalescent prior are biased toward the MSC, especially when the alignments lack phylogenetic signal and Bayesian inference of gene trees is primarily driven by the coalescent prior. Validation analysis should instead compare the simulated gene trees with empirical gene trees estimated from multilocus sequence data without any influence of the MSC (i.e., the posterior gene trees generated independently across loci). In addition, to reduce the influence of substitution models on the fit of the MSC, we perform model validation only for loci that fit the substitution model (Bayesian model validation; Fig. 1). Question 4, model comparison between the concatenation and MSC models, can again be addressed in a Bayesian framework, using Bayes factors (BFs) (Bayesian model comparison; Fig. 1) or other posterior predictive approaches (Lewis et al. 2014). By addressing these questions, we aim to directly compare competing models, especially as they apply to phylogenomic data sets where concatenation might plausibly be applied.
test to handle missing characters (goodness of fit of substitution models; Fig. 1). To evaluate the effect of substitution models on the fit of the MSC, model validation analysis was conducted with different substitution models for the same data sets. Question 3, the adequacy of the MSC, can be addressed using PPS in a Bayesian framework (Reid et al. 2014) implemented in a Bayesian phylogenetic program BEAST (Suchard et al. 2018). Unlike previous studies utilizing sequence data simulated under the MSC model to validate coalescent methods (Kubatko and Degnan 2007), PPS directly evaluates the fit of the MSC model by comparing the posterior gene trees and the gene trees simulated from the MSC (Reid et al. 2014). However, the posterior gene trees generated with a coalescent prior are biased toward the MSC, especially when the alignments lack phylogenetic signal and Bayesian inference of gene trees is primarily driven by the coalescent prior. Validation analysis should instead compare the simulated gene trees with empirical gene trees estimated from multilocus sequence data without any influence of the MSC (i.e., the posterior gene trees generated independently across loci). In addition, to reduce the influence of substitution models on the fit of the MSC, we perform model validation only for loci that fit the substitution model (Bayesian model validation; Fig. 1). Question 4, model comparison between the concatenation and MSC models, can again be addressed in a Bayesian framework, using Bayes factors (BFs) (Bayesian model comparison; Fig. 1) or other posterior predictive approaches (Lewis et al. 2014). By addressing these questions, we aim to directly compare competing models, especially as they apply to phylogenomic data sets where concatenation might plausibly be applied.
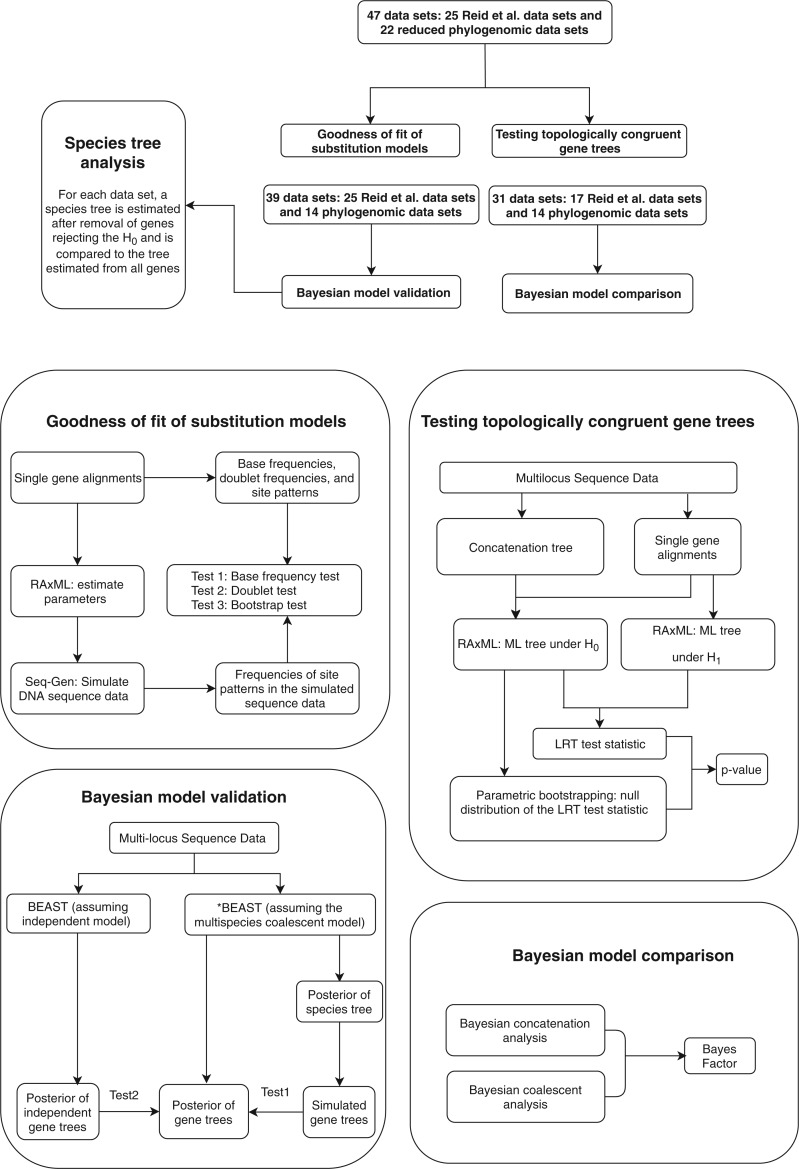
Figure 1.
Flowchart of phylogenetic analyses in this study. The alignments of 47 data sets were used to test the hypothesis of TC gene trees and goodness of fit of substitution models. Model validation and comparison were only performed for the loci that fit the GTRGAMMA model, reducing the number of input data for model validation to 39 (25 Reid et al. data sets and 14 phylogenomic data sets). Because model comparison as implemented in BEAST does not allow missing taxa in any locus, eight Reid et al. data sets were removed, further reducing the number of input data for model comparison to 31 (17 Reid et al. data sets and 14 phylogenomic data sets).
Materials and Methods
Phylogenomic Data Sets
This study consists of 47 empirical data sets (available on Dryad at https://doi.org/10.5061/dryad.7q6q3s0), including the 25 data sets from Reid et al. (2014) and 22 additional data sets (termed “phylogenomic data sets”) across the tree of life. We chose phylogenomic data sets primarily based on their having been sampled from multiple species, usually more than 10 at the level of family or above, for their coverage of at least 50 loci and for their availability in already aligned nexus or phylip format on an easy accessible open access database. We also eased our search by focusing primarily although not exclusively on data sets from the journal Molecular Phylogenetics and Evolution, where a large number of phylogenomic data sets can be found in one place. The 22 phylogenomic data sets were downloaded from the data links available in the original papers (Table 1). The genetic markers of the 22 phylogenomic data sets are highly diversified, including CDS matrices, exons, and UCEs (Table 1). There are 12–207 species in the 22 additional data sets, and the number of loci ranges from 110 to 30,636 (Table 1). Due to computational limits of Bayesian model comparisons (Questions 3 and 4), each of the 22 phylogenomic data sets was reduced to only include the alignments of the 10 most fully populated species across loci, and loci with missing sequences were removed from further analysis. Reducing the number of species in alignments will, if anything, increase gene tree similarity across loci when compared with data sets with the full complement of species, and therefore, increase the fit of the concatenation model to the data. After data reduction, the data sets contained alignments of 36 (Aitken et al. 2017) to 4709 (Wu et al. 2018) loci, each with 10 species (Table 1).
Table 1.
Summary of 22 phylogenomic data sets analyzed here, in addition to those of Reid et al. (2014).
| Data set | OTUs | Loci | Markers |
|---|---|---|---|
| Ant (Blaimer et al. 2018b) | 10/153 | 1509/1763 | UCE |
| Bee (Sann et al. 2018) | 10/95 | 193/195 | CDS |
| Bird (Prum et al. 2015) | 10/198 | 259/259 | CDS |
| Lizard (Blom et al. 2017) | 10/29 | 1831/1852 | Exon |
| Brittlestar (O’Hara et al. 2019) | 10/46 | 407/416 | CDS |
| Butterfly (Espeland et al. 2018) | 10/207 | 325/352 | Exon |
| CarpenterBee (Blaimer et al. 2018a) | 10/179 | 597/753 | UCE |
| Cichlid (McGee et al. 2016) | 10/50 | 924/1043 | UCE |
| Clupeocephalan (Straube et al. 2018) | 10/52 | 48/829 | Exon |
| Cracids (Hosner et al. 2016) | 10/23 | 430/430 | UCE |
| Darter (MacGuigan and Near 2018) | 10/112 | 363/30,636 | RADseq |
| Diplostomoidea (Locke et al. 2018) | 10/12 | 324/517 | UCE |
| Gallopheasant (Meiklejohn et al. 2016) | 10/18 | 1479/1479 | UCE |
| Hemimastigophora (Lax et al. 2018) | 10/61 | 239/351 | CDS |
| Lepanthes (Bogarín et al. 2018) | 10/33 | 334/433 | CDS |
| Mammal2018 (Wu et al. 2018) | 10/90 | 4709/5162 | CDS |
| Mammal2017 (Scornavacca and Galtier 2017) | 10/97 | 108/110 | CDS |
| Metazoan2015 (Whelan et al. 2015) | 10/76 | 36/115 | CDS |
| Shrew (Giarla and Esselstyn 2015) | 10/19 | 966/1112 | UCE |
| Squirrel (McLean et al. 2019) | 10/74 | 3209/3951 | UCE |
| Weevil (Aitken et al. 2017) | 10/67 | 318/521 | CDS |
| Fish (Cui et al. 2013) | 10/27 | 1183/1183 | CDS |
Notes: In the columns OTUs and Loci, the bottom number is the count of taxa (or loci) in the original data set; the top number is the count of taxa (or loci) after data reduction for Questions 3 and 4 (see Materials and Methods section).
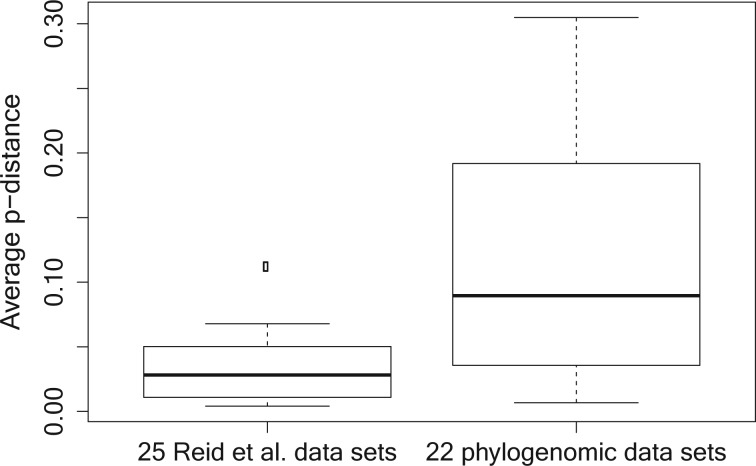
The sequence divergence (i.e., the average pairwise p-distance) of the 22 reduced phylogenomic data sets was significantly higher (P  0.01) than that of the 25 Reid et al. data sets (Appendix Fig. A.1). Indeed, several of the data sets we analyze are at very high taxonomic levels, such as those of metazoans (Whelan et al. 2015; Simion et al. 2017) or mammals (Scornavacca and Galtier 2017; Wu et al. 2018). Some of these data sets, such as those from metazoans, are at such high taxonomic levels, that MSC models have to our knowledge never been applied, perhaps in the mistaken idea that ILS is extremely unlikely to occur among such deep lineages. However, as pointed out by many authors, even if ILS is harder to detect among deep lineages, it is no less likely to occur among deeply diverging than recently diverging lineages, since it is the length of internodes, rather than their depth in time that is most relevant to MSC processes.
0.01) than that of the 25 Reid et al. data sets (Appendix Fig. A.1). Indeed, several of the data sets we analyze are at very high taxonomic levels, such as those of metazoans (Whelan et al. 2015; Simion et al. 2017) or mammals (Scornavacca and Galtier 2017; Wu et al. 2018). Some of these data sets, such as those from metazoans, are at such high taxonomic levels, that MSC models have to our knowledge never been applied, perhaps in the mistaken idea that ILS is extremely unlikely to occur among such deep lineages. However, as pointed out by many authors, even if ILS is harder to detect among deep lineages, it is no less likely to occur among deeply diverging than recently diverging lineages, since it is the length of internodes, rather than their depth in time that is most relevant to MSC processes.
Goodness of Fit of Substitution Models
Let  be the counts of k site patterns in a locus alignment. The random variables
be the counts of k site patterns in a locus alignment. The random variables 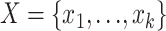 have a multinomial distribution with
have a multinomial distribution with 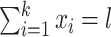 , where l denotes the length of the alignment. Let M be the preselected substitution model. When there is no missing data, the
, where l denotes the length of the alignment. Let M be the preselected substitution model. When there is no missing data, the 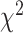 goodness of fit test can evaluate adequacy of model M by comparing the observed and expected counts of site patterns (Reeves 1992; Goldman 1993; Jhwueng 2013). The test statistic is
goodness of fit test can evaluate adequacy of model M by comparing the observed and expected counts of site patterns (Reeves 1992; Goldman 1993; Jhwueng 2013). The test statistic is  , in which
, in which 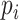 is the probability of site pattern i. The probability
is the probability of site pattern i. The probability  can be estimated under the null hypothesis using the maximum likelihood (ML) estimates of the tree topology, branch lengths, and the parameters in model M. Asymptotically, the test statistic has the
can be estimated under the null hypothesis using the maximum likelihood (ML) estimates of the tree topology, branch lengths, and the parameters in model M. Asymptotically, the test statistic has the 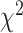 distribution with (k
distribution with (k 1) degrees of freedom. Since this
1) degrees of freedom. Since this 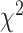 test statistic is based on the frequencies of sites for fully populated characters, sites with missing characters (gaps, ambiguous nucleotides, and unidentified regions) are excluded from analysis, even though only a small portion of nucleotides are missing in each site. To incorporate partially missing sites, a modified
test statistic is based on the frequencies of sites for fully populated characters, sites with missing characters (gaps, ambiguous nucleotides, and unidentified regions) are excluded from analysis, even though only a small portion of nucleotides are missing in each site. To incorporate partially missing sites, a modified 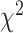 test was developed to calculate the observed and expected counts of site patterns in the presence of missing data (Waddell 2005). We instead calculate the marginal proportion of a site with missing characters and then compare the marginal proportion of the site with its expectation. For example, there are two missing characters in a site
test was developed to calculate the observed and expected counts of site patterns in the presence of missing data (Waddell 2005). We instead calculate the marginal proportion of a site with missing characters and then compare the marginal proportion of the site with its expectation. For example, there are two missing characters in a site 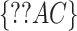 of four species
of four species 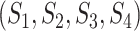 , that is, the nucleotides from species
, that is, the nucleotides from species 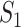 and
and 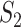 are missing. The marginal proportion
are missing. The marginal proportion 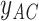 of {AC} in the alignments of
of {AC} in the alignments of 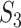 and
and  is given by
is given by  , in which
, in which 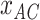 is the count of
is the count of 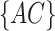 and z is the number of sites without missing characters in the alignment of
and z is the number of sites without missing characters in the alignment of  and
and  . Since a small z indicates a large amount of missing data in the alignment, we arbitrarily ignore sites for which z/l
. Since a small z indicates a large amount of missing data in the alignment, we arbitrarily ignore sites for which z/l 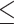 0.8. The test statistic
0.8. The test statistic 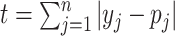 , in which
, in which  is the observed proportion of a site pattern with or without missing characters, and
is the observed proportion of a site pattern with or without missing characters, and 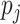 is the probability of the site pattern under the null hypothesis, and n is the number of site patterns for which z/l
is the probability of the site pattern under the null hypothesis, and n is the number of site patterns for which z/l 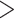 0.8. The null distribution of the test statistic is estimated by parametric bootstrap samples generated from the ML estimates of the tree topology, branch lengths, and the parameters in model M.
0.8. The null distribution of the test statistic is estimated by parametric bootstrap samples generated from the ML estimates of the tree topology, branch lengths, and the parameters in model M.
Marginal tests of base compositions between pairs of taxa (Tavare 1986; Chen et al. 2019) have been found to be more powerful than the 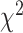 goodness of fit test of the substitution models to phylogenetic data (Waddell et al. 2009). We therefore perform two marginal tests. The first test is to detect heterogeneity of base compositions across species when the observed base frequencies of individual species deviate significantly from the overall average base frequencies across species. Let
goodness of fit test of the substitution models to phylogenetic data (Waddell et al. 2009). We therefore perform two marginal tests. The first test is to detect heterogeneity of base compositions across species when the observed base frequencies of individual species deviate significantly from the overall average base frequencies across species. Let 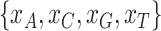 be the observed frequencies of nucleotides A, C, G, and T of a species. The frequency of nucleotide
be the observed frequencies of nucleotides A, C, G, and T of a species. The frequency of nucleotide  is equal to
is equal to 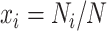 , where
, where  is the number of nucleotide i and N is the total number of nucleotides excluding missing characters in the sequence. Under the null hypothesis of homogeneous substitution models, all species are expected to have the same base frequencies and thus the expected base frequencies under the null hypothesis are estimated by the overall average frequencies
is the number of nucleotide i and N is the total number of nucleotides excluding missing characters in the sequence. Under the null hypothesis of homogeneous substitution models, all species are expected to have the same base frequencies and thus the expected base frequencies under the null hypothesis are estimated by the overall average frequencies 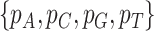 of A, C, G, and T across species. The
of A, C, G, and T across species. The 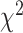 test of the observed frequencies
test of the observed frequencies 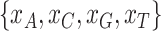 against the expected frequencies
against the expected frequencies 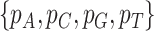 is carried out for each species to detect those species whose base frequencies significantly deviate from the null hypothesis that all species have the same base frequencies. Similarly, the second marginal test is applied to the frequencies of double-nucleotides (doublets) between pairs of species to find pairs of species for which doublet frequencies are inconsistent with the preselected substitution model (Chen et al. 2019). The frequency of doublet
is carried out for each species to detect those species whose base frequencies significantly deviate from the null hypothesis that all species have the same base frequencies. Similarly, the second marginal test is applied to the frequencies of double-nucleotides (doublets) between pairs of species to find pairs of species for which doublet frequencies are inconsistent with the preselected substitution model (Chen et al. 2019). The frequency of doublet 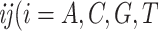 and
and 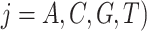 is equal to
is equal to 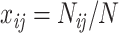 , where
, where 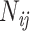 is the number of doublet ij and N is the total number of doublets excluding those with missing characters.
is the number of doublet ij and N is the total number of doublets excluding those with missing characters.
The bootstrap and two marginal tests were conducted to evaluate goodness of fit of the GTRGAMMA model to 47 empirical data sets (Fig. 1). We chose the GTRGAMMA model because the most parameter-rich model (GTRGAMMA in RAxML) is sufficient for reliable phylogenetic inference (Abadi et al. 2019) and a more complex model tends to be a better fit to phylogenomic data than simpler models (Liu et al. 2017). For each locus, the ML estimates of the phylogenetic tree and other parameters were obtained by RAxML v8.2.3 (Stamatakis 2014) using the GTRGAMMA model. Then, 100,000 base pairs of sequence were simulated from the estimated phylogenetic tree using Seq-Gen v1.3.2x (Rambaut and Grassly 1997). The expected frequencies of site patterns were estimated by the corresponding frequencies in the simulated sequences. In addition, 100 bootstrap samples were generated by simulating DNA sequences from the concatenation tree for each locus. If taxa were missing from the loci, they were pruned from the concatenation tree and DNA sequences were simulated from the pruned concatenation tree. The test statistic was calculated for each bootstrap sample. The observed test statistic t* was compared with the bootstrap test statistics 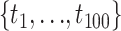 and P-value
and P-value  (
(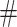 of
of 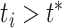 )/100. For the marginal test of base frequencies, the sequence of a species was considered significant if its P-value was less than 0.05 divided by the number of species. A locus was deemed significant if it had at least one significant species. Similarly, for the test of doublet frequencies between pairs of species, a pair of species was significant if its P-value was
)/100. For the marginal test of base frequencies, the sequence of a species was considered significant if its P-value was less than 0.05 divided by the number of species. A locus was deemed significant if it had at least one significant species. Similarly, for the test of doublet frequencies between pairs of species, a pair of species was significant if its P-value was 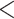 0.05 divided by the number of pairs. Here, a locus was significant if it had at least one significant pair. The bootstrap and two marginal tests were applied to each locus of the 47 data sets. A locus was considered significant if any of the above three tests was significant for the locus.
0.05 divided by the number of pairs. Here, a locus was significant if it had at least one significant pair. The bootstrap and two marginal tests were applied to each locus of the 47 data sets. A locus was considered significant if any of the above three tests was significant for the locus.
Testing for Topologically Congruent Gene Trees
We ask the question whether a single gene tree topology can adequately explain a given multilocus data set, using a variant of the LRT. Similar types of LRTs were developed to test if alternative trees are congruent with the (ML) tree for a single locus (Shimodaira and Hasegawa 1999; Shimodaira 2002). McVay and Carstens (2013) proposed a parametric bootstrap approach to assess the extent to which gene tree variation can be attributed to phylogenetic estimation error. Here, we develop an LRT to evaluate the concatenation assumption of congruent gene trees for multiple loci. Let 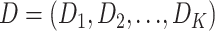 be the concatenated alignments of a multilocus sequences data set, in which
be the concatenated alignments of a multilocus sequences data set, in which 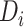 represents the alignments of locus i and K is the count of loci. The tree topology of locus i is denoted by
represents the alignments of locus i and K is the count of loci. The tree topology of locus i is denoted by 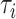 . Under the concatenation model, all loci are assumed to have the same tree topology
. Under the concatenation model, all loci are assumed to have the same tree topology 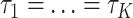 . We develop an LRT to evaluate the null hypothesis that all gene trees have the same topology
. We develop an LRT to evaluate the null hypothesis that all gene trees have the same topology 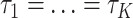 versus the alternative hypothesis that not all gene trees are topologically identical. The test statistic is defined as
versus the alternative hypothesis that not all gene trees are topologically identical. The test statistic is defined as 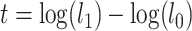 , in which
, in which 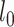 and
and 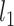 are the likelihoods of the null and alternative hypotheses. Under the null hypothesis, the ML tree is built from the concatenated alignments across loci using RAxML v8.2.3 (Stamatakis 2014) with the GTRGAMMA model (Tavare 1986; Yang 1994). Using the ML tree instead of the true concatenation tree for the null hypothesis may lead to a biased test. However, since the concatenated sequences of phylogenomic data consist of millions of base pairs, the ML tree is very similar, if not identical, to the true concatenation tree. Thus, the bias induced by the topological difference between the ML and true concatenation tree is likely negligible for phylogenomic data. Let
are the likelihoods of the null and alternative hypotheses. Under the null hypothesis, the ML tree is built from the concatenated alignments across loci using RAxML v8.2.3 (Stamatakis 2014) with the GTRGAMMA model (Tavare 1986; Yang 1994). Using the ML tree instead of the true concatenation tree for the null hypothesis may lead to a biased test. However, since the concatenated sequences of phylogenomic data consist of millions of base pairs, the ML tree is very similar, if not identical, to the true concatenation tree. Thus, the bias induced by the topological difference between the ML and true concatenation tree is likely negligible for phylogenomic data. Let  be the log-likelihood of locus i by refitting branch lengths and substitution model parameters to the concatenation tree with missing taxa being removed. The log-likelihood under the null hypothesis is equal to the sum of the log-likelihoods of individual loci, that is,
be the log-likelihood of locus i by refitting branch lengths and substitution model parameters to the concatenation tree with missing taxa being removed. The log-likelihood under the null hypothesis is equal to the sum of the log-likelihoods of individual loci, that is, 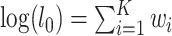 . Refitting branch lengths and model parameters on a fixed tree topology was performed in RAxML using the command line “raxml-HPC-AVX –s datafile –m GTRGAMMA –n outputfile –f e –t fixtree”. To find the log-likelihood of the alternative hypothesis, ML trees were independently built for individual loci using RAxML. Since model parameters include tree topologies, the
. Refitting branch lengths and model parameters on a fixed tree topology was performed in RAxML using the command line “raxml-HPC-AVX –s datafile –m GTRGAMMA –n outputfile –f e –t fixtree”. To find the log-likelihood of the alternative hypothesis, ML trees were independently built for individual loci using RAxML. Since model parameters include tree topologies, the 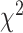 distribution is not a good approximation to the null distribution of the test statistic (Jhwueng et al. 2014). Therefore, the null distribution of the test statistic was approximated by a parametric bootstrap. Bootstrap samples were generated under the null hypothesis by simulating DNA sequences from the concatenation tree pruned for available species at each locus. Since the original alignments include missing characters (gaps, ambiguous nucleotides, and unidentified regions), bootstrap samples should involve a similar pattern of missing characters. Thus, corresponding nucleotides in bootstrap samples were replaced by missing characters. Let
distribution is not a good approximation to the null distribution of the test statistic (Jhwueng et al. 2014). Therefore, the null distribution of the test statistic was approximated by a parametric bootstrap. Bootstrap samples were generated under the null hypothesis by simulating DNA sequences from the concatenation tree pruned for available species at each locus. Since the original alignments include missing characters (gaps, ambiguous nucleotides, and unidentified regions), bootstrap samples should involve a similar pattern of missing characters. Thus, corresponding nucleotides in bootstrap samples were replaced by missing characters. Let 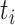 be the value of the test statistic t for the bootstrap sample i = 1, …, B. The log-likelihoods of the null and alternative hypothesis in the test statistic t were generated using RAxML. The values
be the value of the test statistic t for the bootstrap sample i = 1, …, B. The log-likelihoods of the null and alternative hypothesis in the test statistic t were generated using RAxML. The values 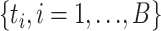 of the test statistic for B bootstrap samples were used to approximate the null distribution of the test statistic t. The P-value was estimated by the proportion of
of the test statistic for B bootstrap samples were used to approximate the null distribution of the test statistic t. The P-value was estimated by the proportion of 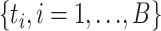 that were greater than or equal to the test statistic t calculated from real data. Rejection of the null hypothesis indicates that some gene trees are incongruent with the concatenation tree. Then, the LRT was further applied to each locus to identify alignments that reject the null (concatenation) tree. Let
that were greater than or equal to the test statistic t calculated from real data. Rejection of the null hypothesis indicates that some gene trees are incongruent with the concatenation tree. Then, the LRT was further applied to each locus to identify alignments that reject the null (concatenation) tree. Let  be the concatenation tree and
be the concatenation tree and 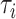 is the gene tree i. The null and alternative hypotheses are
is the gene tree i. The null and alternative hypotheses are 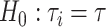 and
and 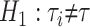 . The test statistic is
. The test statistic is 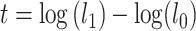 , in which
, in which 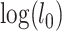 and
and 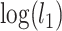 are the log-likelihoods of locus i under the null and alternative hypotheses. The null distribution of the test statistic was approximated by bootstrap samples generated under the null hypothesis and the P-value was equal to the proportion of bootstrap test statistics that are greater than or equal to the observed test statistic. A locus was significant if its P-value is less than or equal to 0.05 divided by the number of loci (Bonferroni correction for multiple comparisons).
are the log-likelihoods of locus i under the null and alternative hypotheses. The null distribution of the test statistic was approximated by bootstrap samples generated under the null hypothesis and the P-value was equal to the proportion of bootstrap test statistics that are greater than or equal to the observed test statistic. A locus was significant if its P-value is less than or equal to 0.05 divided by the number of loci (Bonferroni correction for multiple comparisons).
Bayesian Validation of the Multispecies Coalescent Model
Like Reid et al. (2014), the Bayesian MSC model is here validated by Bayesian predictive simulation. Reid et al. (2014) recommended comparing the posterior coalescent gene trees to the gene trees simulated from the posterior species trees. However, the posterior coalescent gene trees have been influenced by the MSC prior, which is implemented in packages such as BEST (Liu 2008) or *BEAST (Heled and Drummond 2010). The posterior gene trees with an MSC prior are biased toward the MSC model to some extent, compared with gene trees generated without an MSC prior, making this test conservative (i.e., in favor of the MSC). Therefore, in this work, simulated gene trees are compared to posterior gene trees generated without the MSC prior. We validate the MSC model using two tests. The first test, as in Reid et al. (2014), involves two comparisons–comparing the MSC likelihoods of the simulated and posterior coalescent gene trees and comparing the number of deep coalescences of the simulated and posterior coalescent gene trees. The first test is rejected if either or both of the two comparisons reject the MSC model. In the second test, not used by Reid et al. (2014), the posterior gene trees are first estimated independently across loci in BEAST by unlinking the substitution models, clock models, and trees. If the 99.9% posterior credible regions of the log-likelihoods of the independent model and the MSC model do not overlap, we conclude that there is a significant difference between the posterior independent and coalescent gene trees. We infer a poor fit of the MSC model to the data if either or both of the two tests are rejected. Both tests can also be applied to each locus in the data to identify gene trees that significantly deviate from the MSC model.
To alleviate the impact of poorly fitting substitution models on the fit of the MSC, model validation, and comparison were only performed on the loci that fit the assumed substitution model (GTRGAMMA). Since the number of loci in the 25 Reid et al. data sets is insufficient for filtering out the unfit loci, selection of loci that fit the substitution model was only performed on the 22 reduced phylogenomic data sets. After locus selection, 8 of 22 data sets had 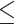 3 loci that fit the substitution model and thus they were removed from further analysis. We then randomly selected 50 loci from the remaining 14 phylogenomic data sets, resulting in a total of 39 data sets (25 Reid et al. data sets
3 loci that fit the substitution model and thus they were removed from further analysis. We then randomly selected 50 loci from the remaining 14 phylogenomic data sets, resulting in a total of 39 data sets (25 Reid et al. data sets  14 phylogenomic data sets with 50 loci) for the model validation analysis (Fig. 1). The xml input files of the 25 data sets from Reid et al. were available in the data package provided by the authors. Reid et al. (2014)’s *BEAST analyses of those data sets assumed HKY and TN93 (+GAMMA) substitution models for individual loci and an MSC prior for gene trees. To evaluate the effect of substitution models on the fit of the MSC model, Bayesian model validation of 25 Reid et al. data sets was conducted again with the GTRGAMMA model. To reduce the effect of substitution models on the overall fit of the MSC for the 14 phylogenomic data sets, the validation analysis was conducted only for loci for which the GTRGAMMA model was a good fit. Consequently, rejections of the MSC imply a poor fit of coalescent assumptions rather than a poor fit of the assumed substitution model. The xml input files of 14 data sets were generated using BEAUti v1.8.4, assuming the GTRGAMMA substitution model for all loci.
14 phylogenomic data sets with 50 loci) for the model validation analysis (Fig. 1). The xml input files of the 25 data sets from Reid et al. were available in the data package provided by the authors. Reid et al. (2014)’s *BEAST analyses of those data sets assumed HKY and TN93 (+GAMMA) substitution models for individual loci and an MSC prior for gene trees. To evaluate the effect of substitution models on the fit of the MSC model, Bayesian model validation of 25 Reid et al. data sets was conducted again with the GTRGAMMA model. To reduce the effect of substitution models on the overall fit of the MSC for the 14 phylogenomic data sets, the validation analysis was conducted only for loci for which the GTRGAMMA model was a good fit. Consequently, rejections of the MSC imply a poor fit of coalescent assumptions rather than a poor fit of the assumed substitution model. The xml input files of 14 data sets were generated using BEAUti v1.8.4, assuming the GTRGAMMA substitution model for all loci.
Two independent runs were carried out for each analysis and convergence was checked by comparing the outputs from two runs. The first 50% of (MCMC) samples were discarded as burn-in. Then, 1000 samples were selected from the remaining MCMC samples and used as input for Bayesian model validation. The first test of Bayesian model validation was conducted using the R package starbeastPPS (Reid et al. 2014). To perform the second test, 39 input data sets were reanalyzed by unlinking the substitution models, clock models, and trees across loci in BEAST, which produced posterior gene trees independently across loci without the MSC prior. The 99.9% credible region of the difference between the log-likelihoods of the independent and coalescent models was calculated in R. The two tests were also applied to each locus to identify gene trees that significantly deviate from the MSC model.
To evaluate the effect of loci rejecting the MSC on species tree estimation, species trees were built from all loci and only loci that did not reject the MSC for each of the 14 phylogenomic data sets using NJst (Liu and Yu 2011) implemented in the R package Phybase (Liu and Yu 2010). This analysis was not performed for the 25 Reid et al. data sets due to their small numbers of loci for species tree estimation. We calculated the Robinson–Foulds (RF) distance (Robinson and Foulds 1981) of two species trees reconstructed for each data set using the function dist.topo in the R package ape (Paradis and Schliep 2019). To evaluate statistical significance of the difference between pairs of species trees with a positive RF distance, bootstrap support values of the incongruent branches were calculated using bootstrap gene trees estimated from alignments. Specifically, bootstrap gene trees were built for each locus and then used as input data to calculate bootstrap NJst trees. The bootstrap support value of a branch was equal to the count of bootstrap NJst trees supporting the clade indicated by the branch. Romiguier et al. (2013) suggested that high GC content may cause problems for phylogenetic inference under the MSC model and that selecting AT-rich loci can improve the resolution of estimated phylogenies. To investigate the association between GC content and poor fit of the MSC, we calculated GC content for loci rejecting and accepting the MSC, respectively. A two-sample t-test was used to find significant difference in GC content between loci rejecting the MSC and those accepting the MSC.
Bayesian Model Comparison for MSC Versus Concatenation
Bayesian model comparison for concatenation versus the MSC was evaluated using BFs (Kass and Raftery 1995), the ratio of marginal likelihoods  , in which D denotes data and
, in which D denotes data and  and
and  are two competing models. Here,
are two competing models. Here, 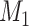 is the MSC model and
is the MSC model and  is the concatenation model. The Bayesian concatenation analyses assumed a partition model by unlinking substitution models and clock models across loci. The marginal log-likelihoods of the Bayesian MSC and concatenation models were estimated using path sampling/stepping-stone sampling with 100 path steps as implemented in BEAST. A value of log(BF)
is the concatenation model. The Bayesian concatenation analyses assumed a partition model by unlinking substitution models and clock models across loci. The marginal log-likelihoods of the Bayesian MSC and concatenation models were estimated using path sampling/stepping-stone sampling with 100 path steps as implemented in BEAST. A value of log(BF)  10 indicates that the Bayesian MSC model
10 indicates that the Bayesian MSC model 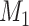 is strongly favored by the data versus the Bayesian concatenation model
is strongly favored by the data versus the Bayesian concatenation model  . Model comparison was applied to the 39 data sets used in the Bayesian model validation analysis. Since model comparison implemented in BEAST does not allow missing taxa in any locus, eight data sets with missing data were removed, further reducing the number of input data for the model comparison analysis to 31 (Fig. 1).
. Model comparison was applied to the 39 data sets used in the Bayesian model validation analysis. Since model comparison implemented in BEAST does not allow missing taxa in any locus, eight data sets with missing data were removed, further reducing the number of input data for the model comparison analysis to 31 (Fig. 1).
To demonstrate that model assumptions may influence species tree inference, we reconstructed species trees for four phylogenomic data sets using concatenation and a coalescent method (NJst). These data sets were chosen based on gene tree heterogeneity so as to illustrate the potential for differing results from coalescent and concatenation approaches. In addition, we subsampled 25%, 50%, and 75% of loci from the original phylogenomic data, and compared the species trees built from the subsamples with those for the full phylogenomic data (Edwards et al. 2016). The concatenation trees were estimated by RAxML with the GTRCAT model. The NJst trees were built using the function sptree.njst in Phybase. We calculated the bootstrap support values for each estimated species tree. Two estimated species trees were deemed significantly incongruent if they have a conflicting branch with bootstrap support of 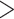 70. Subsampling was repeated 10 times and we reported the proportion of subsamples (out of 10) for which the estimated species tree was significantly incongruent with the species tree built from the full phylogenomic data.
70. Subsampling was repeated 10 times and we reported the proportion of subsamples (out of 10) for which the estimated species tree was significantly incongruent with the species tree built from the full phylogenomic data.
Results
Goodness of Fit of Substitution Models
There was a total of 20,032 loci (CDS, UCEs, or exons) throughout the 47 empirical data sets; 241 loci from the 25 Reid et al. data sets and 19,791 loci from the 22 phylogenomic data sets. The marginal test of base frequencies identified a total of 1362 (7%) loci/alignments (or 9% loci per data set in Fig. 2a) for which at least one sequence significantly deviates from the average base frequencies expected from the GTRGAMMA model. The doublet test indicated that 6990 (35%) loci/alignments (or 51% loci per data set in Fig. 2a) have at least a pair of species whose doublet patterns are significantly different from the patterns expected from the GTRGAMMA model. The marginal test favors complex substitution models, because a complex model has a higher likelihood than a simple model, indicating that the expected frequencies under the complex model are more consistent with the observed frequencies of site patterns in the alignments. Thus, rejection of the GTRGAMMA model suggests that a more complex substitution model should be fit to the data. In the bootstrap test for site patterns, the GTRGAMMA model fails to fit the alignments of 5718 (24%) loci across the 47 data sets (or 34% loci per data set in Fig. 2a). The doublet test appears to be more likely than the bootstrap test for site patterns to reject the GTRGAMMA model (Fig. 2a), indicating the necessity of marginal tests for goodness of fit of substitution models. Because the doublet test is more likely to reject the GTRGAMMA model than the other two tests, the intersection test (the intersection of three tests, i.e., at least one of two marginal tests and the bootstrap test reject the GTRGAMMA model) appears to be primarily driven by the doublet test (Fig. 2a). Overall, nearly half of the alignments (8775 loci or 44%) were found significant (P 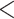 0.05) in the intersection test, and the proportion of significant loci per data set identified by the intersection test ranges from 6% to 100% across the 47 data sets (Fig. 2a). A two-sample t-test finds no significant difference in the proportion of loci rejecting the GTRGAMMA model between the 25 Reid et al. data sets and the 22 phylogenomic data sets (Fig. 2b).
0.05) in the intersection test, and the proportion of significant loci per data set identified by the intersection test ranges from 6% to 100% across the 47 data sets (Fig. 2a). A two-sample t-test finds no significant difference in the proportion of loci rejecting the GTRGAMMA model between the 25 Reid et al. data sets and the 22 phylogenomic data sets (Fig. 2b).
Figure 2.
Goodness of fit of substitution models for 47 data sets. a) The violin boxplot of the proportion of loci rejecting the GTRGAMMA model in 47 data sets by the base frequency test, doublet test, bootstrap test, and the intersection of three tests (i.e., the intersection test), respectively. b) The violin boxplot of the proportion of loci rejecting the GTRGAMMA model for the 25 Reid et al. data sets and the 22 phylogenomic data sets. A two-sample t-test shows no significant difference between the two sets of data (P  0.96). c) Boxplots of GC content of loci rejecting or accepting the GTRGAMMA model. d) Boxplots of informative sites of loci rejecting or accepting the GTRGAMMA model. e) Logistic regression of whether a locus rejects the GTRGAMMA model (response variable) versus GC content and informative sites (two explanatory variables). The y-axis is the count of data sets with a negative or positive coefficient of GC content (or number of informative sites, IS) estimated in the logistic regression. The bars in dark gray denote the count of data sets for which the coefficient (negative or positive) of GC (or informative sites) is significant (P
0.96). c) Boxplots of GC content of loci rejecting or accepting the GTRGAMMA model. d) Boxplots of informative sites of loci rejecting or accepting the GTRGAMMA model. e) Logistic regression of whether a locus rejects the GTRGAMMA model (response variable) versus GC content and informative sites (two explanatory variables). The y-axis is the count of data sets with a negative or positive coefficient of GC content (or number of informative sites, IS) estimated in the logistic regression. The bars in dark gray denote the count of data sets for which the coefficient (negative or positive) of GC (or informative sites) is significant (P 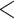 0.05) in the logistic regression.
0.05) in the logistic regression.
To understand the causes of poor substitution model fit, we investigated the relationship between GC content (and proportion of informative sites) and the rejection of the GTRGAMMA model. A two-sample t-test suggests that the proportions of GC content and informative sites of loci rejecting the GTRGAMMA model are significantly higher (P 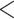 0.05) than those for loci that fit the GTRGAMMA model (Fig. 2c and d). We fitted a logistic regression for all loci across the 47 data sets, where nonsignificance or significance of a locus in the intersection test is the binary response variable, and the proportions of GC content and informative sites are two explanatory variables. In the fitted logistic regression, the coefficients of two explanatory variables are significantly negative with P-value
0.05) than those for loci that fit the GTRGAMMA model (Fig. 2c and d). We fitted a logistic regression for all loci across the 47 data sets, where nonsignificance or significance of a locus in the intersection test is the binary response variable, and the proportions of GC content and informative sites are two explanatory variables. In the fitted logistic regression, the coefficients of two explanatory variables are significantly negative with P-value 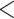 0.01. We further fit a logistic regression to each of the 47 data sets. The coefficient of GC content is negative/positive for 29/18 data sets, among which 6/1 negative/positive coefficients are significant at the
0.01. We further fit a logistic regression to each of the 47 data sets. The coefficient of GC content is negative/positive for 29/18 data sets, among which 6/1 negative/positive coefficients are significant at the 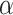 level of 5% (Fig. 2e). Similarly, the coefficient for the number of informative sites is negative/positive for 33/14 data sets, among which 14/0 negative/positive coefficients are significant (Fig. 2e). The preponderance of significantly negative coefficients indicates that a higher GC content and/or proportion of informative sites tends to increase the chance of a poor fit of the GTRGAMMA substitution model.
level of 5% (Fig. 2e). Similarly, the coefficient for the number of informative sites is negative/positive for 33/14 data sets, among which 14/0 negative/positive coefficients are significant (Fig. 2e). The preponderance of significantly negative coefficients indicates that a higher GC content and/or proportion of informative sites tends to increase the chance of a poor fit of the GTRGAMMA substitution model.
Testing Topologically Congruent Gene Trees
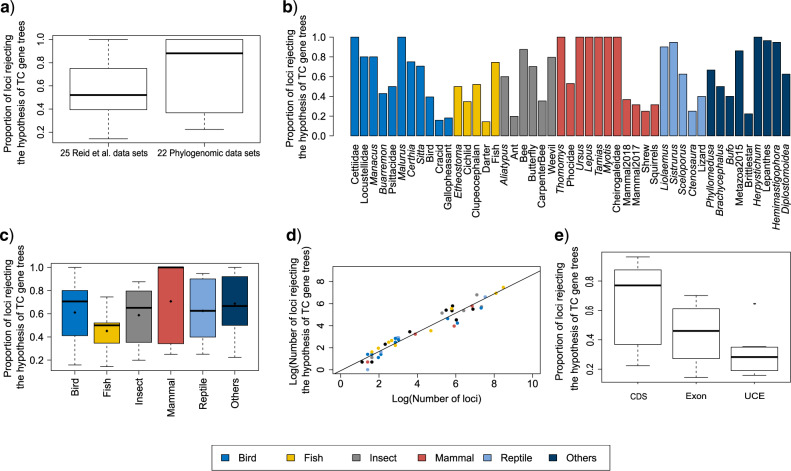
The LRT for TC gene trees rejected the null hypothesis of tree congruence for all 47 empirical data sets with P 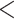 0.05. Thus, all empirical data sets in this study strongly favor the alternative hypothesis of incongruent gene trees, a pattern that cannot be adequately explained by gene tree estimation errors. The P-values of the data sets with 10 or more loci are very close to 0, indicating that the assumption of TC gene trees is rarely satisfied for phylogenomic data, which often involve thousands of loci.
0.05. Thus, all empirical data sets in this study strongly favor the alternative hypothesis of incongruent gene trees, a pattern that cannot be adequately explained by gene tree estimation errors. The P-values of the data sets with 10 or more loci are very close to 0, indicating that the assumption of TC gene trees is rarely satisfied for phylogenomic data, which often involve thousands of loci.
A two-sample t-test finds no significant difference (P  0.10) in the proportion of loci rejecting the null hypothesis of TC gene trees between the 22 phylogenomic data sets and the 25 Reid et al. data sets (Fig. 3a). The topological congruence LRT on individual loci suggests that 38% of gene trees across 47 data sets are statistically incongruent with the concatenation tree (Fig. 3b). When the 47 data sets are grouped into six categories mammals (11), birds (11), insects (6), fish (5), reptiles (5), and others (9), the analysis of variance (ANOVA) finds no significant difference in the proportion of loci rejecting the hypothesis of TC gene trees among six groups (Fig. 3c). Both a two-sample t-test and ANOVA indicate that the proportion of loci rejecting the hypothesis of gene tree congruence is similar across groups and data sets. A linear regression line was fit for the log scale of the number of incongruent loci rejecting the hypothesis of TC gene trees (y) versus the log scale of the number of loci (x), that is,
0.10) in the proportion of loci rejecting the null hypothesis of TC gene trees between the 22 phylogenomic data sets and the 25 Reid et al. data sets (Fig. 3a). The topological congruence LRT on individual loci suggests that 38% of gene trees across 47 data sets are statistically incongruent with the concatenation tree (Fig. 3b). When the 47 data sets are grouped into six categories mammals (11), birds (11), insects (6), fish (5), reptiles (5), and others (9), the analysis of variance (ANOVA) finds no significant difference in the proportion of loci rejecting the hypothesis of TC gene trees among six groups (Fig. 3c). Both a two-sample t-test and ANOVA indicate that the proportion of loci rejecting the hypothesis of gene tree congruence is similar across groups and data sets. A linear regression line was fit for the log scale of the number of incongruent loci rejecting the hypothesis of TC gene trees (y) versus the log scale of the number of loci (x), that is, 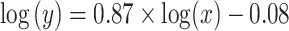 with a significant (P
with a significant (P 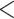 0.01) positive correlation between
0.01) positive correlation between 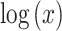 and
and  (Fig. 3d). This result is consistent with the previous conclusion that phylogenomic data sets with more loci are more likely to reject the assumption of TC gene trees; namely, the observed gene tree variation cannot be adequately explained by gene tree estimation error. Moreover, both ANOVA and linear regression analyses suggest a constant and high proportion (38%) of loci rejecting the assumption of TC gene trees across 47 data sets, providing strong evidence for violation of the concatenation assumption of congruent gene trees in phylogenomic data across the tree of life. When the 22 phylogenomic data sets are grouped by data types–CDS (10), exonic (4), and UCEs (8), a t-tests for pairwise comparisons find no significant difference (P
(Fig. 3d). This result is consistent with the previous conclusion that phylogenomic data sets with more loci are more likely to reject the assumption of TC gene trees; namely, the observed gene tree variation cannot be adequately explained by gene tree estimation error. Moreover, both ANOVA and linear regression analyses suggest a constant and high proportion (38%) of loci rejecting the assumption of TC gene trees across 47 data sets, providing strong evidence for violation of the concatenation assumption of congruent gene trees in phylogenomic data across the tree of life. When the 22 phylogenomic data sets are grouped by data types–CDS (10), exonic (4), and UCEs (8), a t-tests for pairwise comparisons find no significant difference (P  0.1) for the proportion of loci rejecting the assumption of TC gene trees between the CDS and exon groups, but the proportions of both groups are significantly (P
0.1) for the proportion of loci rejecting the assumption of TC gene trees between the CDS and exon groups, but the proportions of both groups are significantly (P 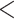 0.01) higher than that of the UCE group (Fig. 2e). This result indicates that the congruent gene tree assumption of the concatenation model is more likely to hold for the UCE data than for the CDS and exon data.
0.01) higher than that of the UCE group (Fig. 2e). This result indicates that the congruent gene tree assumption of the concatenation model is more likely to hold for the UCE data than for the CDS and exon data.
Figure 3.
LRT for topologically congruent gene trees. a) Boxplots of the proportion of loci rejecting the hypothesis of TC gene trees for 25 Reid et al. data sets and 22 phylogenomic data sets. A two-sample t-test shows no significant difference (P  0.10) in the proportion of loci rejecting the hypothesis of TC gene trees between the two sets of data. b) Proportion of loci rejecting the hypothesis of TC gene trees across the 47 data sets. c) Proportion of loci rejecting the hypothesis of TC gene trees in six taxonomic groups. The 47 data sets fall into six groups (bird, mammal, insect, fish, reptile, and others). The filled black diamond represents the average proportion of loci rejecting the hypothesis of TC gene trees in each group. ANOVA finds no significant difference (P
0.10) in the proportion of loci rejecting the hypothesis of TC gene trees between the two sets of data. b) Proportion of loci rejecting the hypothesis of TC gene trees across the 47 data sets. c) Proportion of loci rejecting the hypothesis of TC gene trees in six taxonomic groups. The 47 data sets fall into six groups (bird, mammal, insect, fish, reptile, and others). The filled black diamond represents the average proportion of loci rejecting the hypothesis of TC gene trees in each group. ANOVA finds no significant difference (P  0.71) in the proportion of loci rejecting the hypothesis of TC gene trees among the six groups. d) A linear regression line fitted for the log of the number of loci rejecting the hypothesis of TC gene trees (y) versus the log of the number of loci (x). e) Proportion of loci rejecting the hypothesis of TC gene trees for different data types (CDS, Exon, and UCE).
0.71) in the proportion of loci rejecting the hypothesis of TC gene trees among the six groups. d) A linear regression line fitted for the log of the number of loci rejecting the hypothesis of TC gene trees (y) versus the log of the number of loci (x). e) Proportion of loci rejecting the hypothesis of TC gene trees for different data types (CDS, Exon, and UCE).
To reduce the potential bias caused by an unfit substitution model, the LRT was only applied to the loci that fit the GTRGAMMA model. We filtered out 27 data sets with 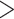 5 loci that fit the GTRGAMMA model and applied the LRT to the remaining 20 data sets. The null hypothesis of tree congruence was rejected for all 20 data sets with P-value
5 loci that fit the GTRGAMMA model and applied the LRT to the remaining 20 data sets. The null hypothesis of tree congruence was rejected for all 20 data sets with P-value 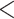 0.05. The LRT on individual loci suggests that 46% of gene trees across the 20 data sets are statistically incongruent with the concatenation tree, which is lower (but not significantly so) than the proportion (48%) when the LRT was applied to all loci of the 20 data sets (Appendix Fig. A.2).
0.05. The LRT on individual loci suggests that 46% of gene trees across the 20 data sets are statistically incongruent with the concatenation tree, which is lower (but not significantly so) than the proportion (48%) when the LRT was applied to all loci of the 20 data sets (Appendix Fig. A.2).
Bayesian Model Validation
Coalescent methods have been widely used for estimating species trees from phylogenomic data. Due to computational constraints, however, few studies have evaluated the fit of the MSC to the multilocus sequences. Here, we validate the MSC model using two tests based on Bayesian predictive simulation. The first test (i.e., PPS proposed by Reid et al. (2014)) compares the simulated gene trees with the posterior coalescent gene trees generated with the MSC prior, whereas the second test (i.e., the independent test) compares the posterior coalescent gene trees with the posterior independent gene trees generated with the independent prior. The analysis of the 25 Reid et al. data sets found that 8 (32%) data sets failed either or both of the two tests (Fig. 4a), among which three data sets were also found to poorly fit to the MSC by Reid et al. (2014; Certhiidae, Tamias, and Aliatypus). However, the xml input files provided by Reid et al. (2014) assumed the HKY and TN93 (+GAMMA) substitution models for all loci. When the *BEAST analyses were rerun with the GTRGAMMA model, only two data sets provided were rejected by either or both of the two tests (Table 2). Thus, the choice of substitution models has major effects on the fit of the MSC. In addition, Bayesian model validation for the 14 phylogenomic data sets for which the GTRGAMMA model was a good fit found that 12 data sets failed the first test and all 14 data sets failed the second test. Thus, the MSC model failed to fit all 14 phylogenomic data sets (Fig. 4a). Since these 14 data sets have more loci than the Reid et al. data sets, this result implies that phylogenomic data with more loci are more likely to reject the MSC. In addition, Bayesian model validation for individual loci of the 14 phylogenomic data sets found that 10.88% of loci rejected the MSC (Fig. 4b), significantly higher (P 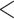 0.01) than the proportion (4.17%) for the 25 Reid et al. data sets, indicating that the probability of a locus rejecting the MSC increases as the number of loci grows.
0.01) than the proportion (4.17%) for the 25 Reid et al. data sets, indicating that the probability of a locus rejecting the MSC increases as the number of loci grows.
Figure 4.
Two tests of Bayesian model validation. The first test proposed in Reid et al. (2014) compares the simulated and posterior coalescent gene tree. The second test compares the gene trees estimated with the coalescent prior and those estimated with the independent prior. The MSC model is a poor fit to the data if either or both of the two tests are rejected. a) The proportion of data sets rejecting the MSC model. Thirty-two percent of the 25 Reid et al. data sets and 100% of the 14 phylogenomic data sets reject the MSC model. b) The proportion (10.88%) of loci rejecting the MSC for 22 phylogenomic data sets is significantly (P 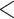 0.01) higher than the proportion (4.17%) of loci in 25 Reid et al. data sets that reject the MSC model. c) Scatter plot of the RF distance versus the proportion of loci rejecting the MSC model. The RF distance between two species trees built from all loci and only loci that fit to the MSC is calculated for 14 phylogenomic data sets; RF = 0 for 9 data sets, RF = 2 for 4, RF = 4 for 1 data set. The number below each point is the bootstrap support value on the corresponding incongruent branch in two species trees. Note that two points with RF = 2 are overlapping, and two values below the point with RF = 4 (i.e., two incongruent branches) are the bootstrap support values on two incongruent branches. d) Testing the association between GC content and poor fit of the MSC. We calculated the average GC content of loci rejecting or accepting the MSC for two phylogenomic data sets with large numbers of loci rejecting the MSC (Birds and mammal 2017). We performed a two-sample t-test for the overall average GC content (combining two data sets) and the average GC content of each of two data sets, respectively. All three tests found no significant difference (P
0.01) higher than the proportion (4.17%) of loci in 25 Reid et al. data sets that reject the MSC model. c) Scatter plot of the RF distance versus the proportion of loci rejecting the MSC model. The RF distance between two species trees built from all loci and only loci that fit to the MSC is calculated for 14 phylogenomic data sets; RF = 0 for 9 data sets, RF = 2 for 4, RF = 4 for 1 data set. The number below each point is the bootstrap support value on the corresponding incongruent branch in two species trees. Note that two points with RF = 2 are overlapping, and two values below the point with RF = 4 (i.e., two incongruent branches) are the bootstrap support values on two incongruent branches. d) Testing the association between GC content and poor fit of the MSC. We calculated the average GC content of loci rejecting or accepting the MSC for two phylogenomic data sets with large numbers of loci rejecting the MSC (Birds and mammal 2017). We performed a two-sample t-test for the overall average GC content (combining two data sets) and the average GC content of each of two data sets, respectively. All three tests found no significant difference (P 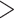 0.3) in GC content between loci rejecting the MSC and loci accepting the MSC.
0.3) in GC content between loci rejecting the MSC and loci accepting the MSC.
Table 2.
Bayesian model validation for the 25 data sets in Reid et al. (2014).
| Data set | starbeastPPS | Independent test | GTRGAMMA | |
|---|---|---|---|---|
| starbeastPPS | Independent test | |||
| Aliatypus | *** | *** | NS | NS |
| Certhiidae | ** | *** | **** | *** |
| Cheirogaleidae | NS | *** | NS | NS |
| Liolaemus | NS | *** | NS | NS |
| Malurus | NS | *** | NS | NS |
| Sceloporus | NS | *** | NS | NS |
| Sitta | NS | *** | NS | NS |
| Tamias | **** | NS | **** | NS |
Notes: The validation analysis involves two tests–starbeastPPS and the independent test. Significance symbols * 0.05, **
0.05, ** 0.025, ***
0.025, ***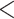 0.01, ****
0.01, **** 0.001, and NS denotes nonsignificant. The last column GTRGAMMA indicates that the Bayesian model validation analyses assuming HKY and TN93
0.001, and NS denotes nonsignificant. The last column GTRGAMMA indicates that the Bayesian model validation analyses assuming HKY and TN93 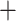 GAMMA were reconducted with the GTRGAMMA model.
GAMMA were reconducted with the GTRGAMMA model.
To evaluate the effect of loci rejecting the MSC on species tree estimation, two species trees were reconstructed, one from all loci and one from only loci that fit to the MSC for each of 14 phylogenomic data sets. A majority (9) of 14 data sets produced two identical species trees (i.e., RF = 0), whereas RF = 2 for 4 data sets (Ant, Cracid, Mammal2017, Squirrel) and RF = 4 for 1 data set (Fig. 4c). Note that RF = 2 or 4 indicates only 1 or 2 conflicting branches in two species trees. Since the incongruent branches are not strongly supported (bootstrap support values 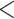 60), the conflict between two different species trees is not significant. This analysis suggests that including loci that fail to fit the MSC has little impact on species tree estimation when a small portion (10.88%) of loci rejects the MSC.
60), the conflict between two different species trees is not significant. This analysis suggests that including loci that fail to fit the MSC has little impact on species tree estimation when a small portion (10.88%) of loci rejects the MSC.
To investigate the association between GC content and poor fit of the MSC, we calculated the average GC content of loci rejecting or accepting the MSC for two phylogenomic data sets for which the number of loci rejecting the MSC is large (Birds and mammal 2017, in which the number of loci rejecting the MSC is 10 and 17, respectively; Fig. 4d). Other phylogenomic data sets contain insufficient number of loci rejecting the MSC for the analysis. A two-sample t-test for the overall average GC content (combining two data sets) and the average GC content of each of two data sets unanimously found that the difference in GC content between loci rejecting the MSC and loci accepting the MSC was not significant (Fig. 4d), suggesting little evidence for a positive association between high GC content and poor fit of the MSC.
Bayesian Model Comparison for MSC Versus Concatenation
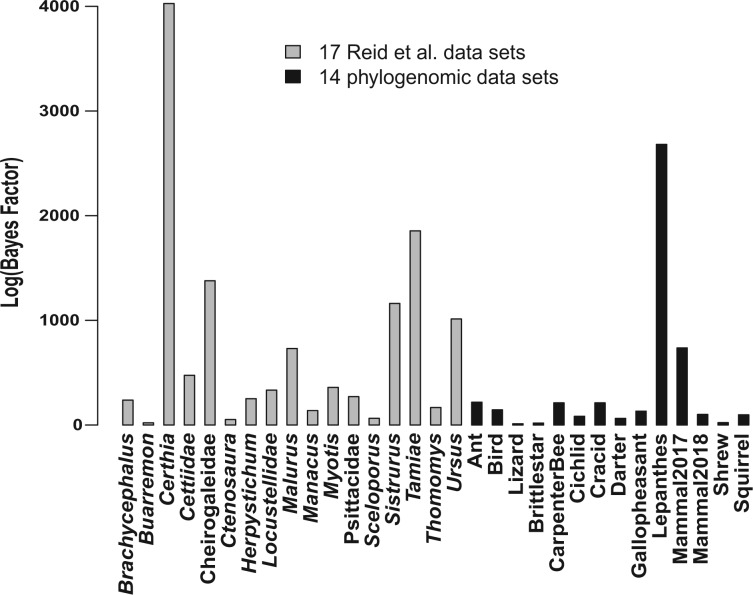
Bayesian model comparison was applied to 31 data sets for which there was no missing data, including 17 Reid et al. data sets and 14 phylogenomic data sets. The BFs (on logarithmic scale) of 26 data sets are greater than 100 and the BFs of the remaining 5 data sets are between 15 and 90. Overall, the high BFs imply that all 31 data sets strongly favor the MSC rather than the concatenation model (Fig. 5). This Bayesian model comparison is consistent with the LRT results for congruent gene trees, which reject the concatenation assumption of congruent gene trees and thus favor the MSC for all 47 data sets.
Figure 5.
Bayesian model comparison. The log-scale Bayes factors of coalescent versus concatenation (unlinking substitution model parameters) models for 31 data sets, including 17 Reid et al. data sets and 14 phylogenomic data sets.
To demonstrate the impact of model assumptions on species tree inference, species trees were estimated for four phylogenomic data sets (Cracids, 23 species and 430 loci; Gallophesants, 18 species and 1479 loci; Lizards, 29 species and 1852 loci; and Shrews, 19 species and 1112 loci, Table 1) using concatenation and a coalescent method NJst. We found three data sets (Cracids, Gallophesants, and Lizard) for which the concatenation trees were significantly incongruent with the corresponding NJst trees (Appendix Fig. A.3), indicating that different models may yield conflict species trees. In the subsampling analysis, the average proportion of significantly incongruent concatenation trees across four data sets is 0.19, much higher than the average proportion (0.008) of significantly incongruent NJst trees (Appendix Fig. A.4), suggesting that concatenation is more likely than coalescent methods to produce incorrect relationships with high bootstrap support values, a pattern that has been noted elsewhere (Kubatko and Degnan 2007; Song et al. 2012; Liu et al. 2015a; Edwards 2016).
Discussion and Conclusions
Model validation and comparison are essential to accurate phylogenetic inference for genome-scale sequence data. Many recent disputes about the utility of the MSC model in phylogenomics have rested on perceived model violations of the MSC, rather than direct tests of the explanatory power of the MSC versus concatenation. Here, we developed and implemented a set of statistical tests to evaluate the adequacy of substitution models, the concatenation model, and the MSC model. In particular, we tried to distinguish two possible sources of rejection of the MSC in empirical data sets: rejection due to violation of the substitution model and rejection due to violation of the MSC. The LRT results for congruent gene trees reveals strong evidence in 47 data sets against the concatenation assumption of congruent gene trees across loci. Crucially, this test suggests that the gene tree variation is real and cannot be explained simply by gene tree estimation error, a point of increasing concern among skeptics of the MSC model (Richards et al. 2018). This result is consistent with the subsequent Bayesian model comparisons, which unanimously favored the MSC over concatenation for all phylogenomic data sets under consideration. Moreover, the proportion of gene trees significantly deviating from the concatenation tree (38%) is consistently high across taxonomic groups (bird, fish, mammal, insect, reptile, and others), and our linear regressions suggest that the concatenation assumption of congruent gene trees is more seriously violated as the number of loci continues to grow in phylogenomic data across the tree of life (Bravo et al. 2019).
The fact that Bayesian model comparison strongly favors the coalescent over concatenation does not necessarily validate the use of the MSC model for analyzing phylogenomic data. In our Bayesian model validation, the MSC model is a good fit for the majority of data sets in Reid et al. (2014), but the choice of substitution models has a strong influence on the fit of the MSC model. To alleviate the effect of substitution models, we applied Bayesian model validation to the loci of the 14 phylogenomic data sets that fit the assumed substitution model. The MSC failed to completely fit all loci in the 14 phylogenomic data sets, but the proportion of loci rejecting the MSC was only 11% ( 12%), significantly smaller than those for substitution models (44%) and concatenation models (38%). Thus, deficiencies in the fit of data to substitution models and to concatenation models appear to be much more severe than the fit to the MSC model, suggesting that more attention should be given to appropriately modeling the evolution of DNA sequences (i.e., substitution models) and gene tree variation, though continuous efforts for improving models at the level of both sequences and gene trees are ultimately desirable.
12%), significantly smaller than those for substitution models (44%) and concatenation models (38%). Thus, deficiencies in the fit of data to substitution models and to concatenation models appear to be much more severe than the fit to the MSC model, suggesting that more attention should be given to appropriately modeling the evolution of DNA sequences (i.e., substitution models) and gene tree variation, though continuous efforts for improving models at the level of both sequences and gene trees are ultimately desirable.
An empirical study of placental mammals (Romiguier et al. 2013) suggested that GC-rich regions perform poorly in phylogenetic analysis, perhaps due to higher rates of gene conversion and recombination, which may be problematic for species tree inference under the MSC model. Our analysis, however, finds no convincing evidence for a positive association between high GC content and poor fit of the MSC. Instead, we find that high GC content is strongly associated with poor fit of substitution models. Thus, the shifting phylogenetic relationships of placental mammals for GC-rich regions found by Romiguier et al. (2013) may be caused not by poor fit of the MSC, but the conflicts among gene trees due to poorly fitted substitution models (see also Romiguier and Roux 2017).
Stochastic models for phylogenomic data should consider the cumulative effect of the mutation process of nucleotides (molecular evolution) and biological processes rooted in population genetics that have played important roles in the evolution of species. Some have argued (Edwards 2009; Liu et al. 2015a) that, among the relevant biological processes, the coalescence process, which assumes random drift, should serve as the null model, and other biological factors, such as gene flow and hybridization, can be added to the null model if the null model cannot adequately explain the observed gene tree variation. As the number of loci continues to increase, some loci are bound to reject the MSC model. Several authors (Brown and Thomson 2017; Shen et al. 2017; Gatesy et al. 2019) have suggested that a small number of extremely influential loci can significantly change the estimates of phylogenetic trees, at least with some coalescent methods. Our analysis indicates that if the loci rejecting the MSC only account for a small proportion of the empirical data (e.g.,  % in this study), the MSC model can still be applied to entire data sets or to data sets purged of the loci that violate the MSC. On the other hand, a large number of loci rejecting the MSC suggests that additional biological phenomena may have occurred and must be added to the stochastic model when analyzing such data sets. Similarly, soundness of the concatenation model depends on the proportion of loci that violate the assumption of homogeneous gene trees.
% in this study), the MSC model can still be applied to entire data sets or to data sets purged of the loci that violate the MSC. On the other hand, a large number of loci rejecting the MSC suggests that additional biological phenomena may have occurred and must be added to the stochastic model when analyzing such data sets. Similarly, soundness of the concatenation model depends on the proportion of loci that violate the assumption of homogeneous gene trees.
Mathematical models are variably robust to violations of assumptions. Several authors have identified numerous putative biological violations of the MSC in empirical data sets, including recombination within loci, pseudoconcatenation of loci such as occurs in transcriptome data as well as natural selection (Gatesy and Springer 2014; Scornavacca and Galtier 2017). However, even in these data sets, despite numerous putative violations of the MSC, the MSC is a better fit than concatenation, suggesting that violations of the MSC may not recommend falling back on concatenation as an alternative method of analysis (Liu et al. 2015a; Edwards 2016). The analysis of empirical data in this study suggests that, although 11% of loci reject the MSC, there is no significant difference between the species trees estimated from all loci and only loci that fit the MSC model. Thus, consistent with other work (Liu et al. 2015b; Xi et al. 2016; Nute et al. 2018), we find that gene tree-based coalescent methods are robust to a certain degree of violation of coalescent assumptions and other biases (but see: Simmons and Gatesy 2015; Meiklejohn et al. 2016; Simmons et al. 2016). In this study, model validation and species tree analyses were conducted on reduced phylogenomic data sets of 50 loci and 10 species each. Our analyses suggest that the concatenation assumption of congruent gene trees rarely holds for phylogenomic data with more than 10 loci. Thus, for large phylogenomic data sets, model comparisons are expected to consistently and more strongly favor the coalescent model over the concatenation model. Adding species in phylogenomic data will introduce additional gene tree variation caused by gene flow, gene duplication/loss, and other factors. Unlike increasing numbers of loci, growth in the number of taxa in phylogenomic data is likely to increase the proportion of loci rejecting the MSC. When the majority of loci do not support the MSC, coalescent methods will eventually fail to accurately reconstruct species trees from the full phylogenomic data, even though model comparison will still favor the MSC over the concatenation model. In such cases, MSC network models, in which gene flow and lineage merging are incorporated, may better fit phylogenomic data sets than the standard MSC model (Wen et al. 2016; Bastide et al. 2018; Blair and Ane 2019).
Acknowledgments
We thank Noah Reid for sharing 25 multilocus sequence data and the xml *BEAST input files, three anonymous reviewers for helpful comments on the manuscript, and Bryan Carstens for the valuable comments. We thank Georgia Advanced Computing Research Center (GACRC) for their computing resource.
Appendix
Figure A.1.
Boxplots for the sequence divergence of 25 Reid et al. data sets and 22 reduced phylogenomic data sets analyzed in this article. Sequence divergence is measured by the average pairwise p-distance (i.e., the proportion of different nucleotides between two sequences). A two-sample t-test finds a significant difference (P  0.01) in sequence divergence between 25 Reid et al. data sets and 22 reduced phylogenomic data sets.
0.01) in sequence divergence between 25 Reid et al. data sets and 22 reduced phylogenomic data sets.
Figure A.2.
Testing congruent gene trees for the loci that fit the GTRGAMMA model. The LRT for congruent gene trees was applied to the loci of 20 data sets that fit the GTRGAMMA model. The gray bars are the proportions of loci rejecting the hypothesis of congruent gene trees when the LRT was applied to all loci. The black bars are the proportions of loci rejecting the hypothesis of congruent gene trees when the LRT was only applied to the loci that fit the GTRGAMMA model.
Figure A.3.
The concatenation and NJst trees for Cracids, Gallopheasants, Lizard, and Shrews. The species trees are built for the four data sets using concatenation and a coalescent method NJst. The numbers at the internal nodes are bootstrap support values.
Figure A.4.
The subsampling analysis for Cracids, Gallophesants, Lizard, and Shrews data sets. We sampled 25%, 50%, and 75% of loci from each data set. Species trees were reconstructed for each sample using the concatenation and coalescent (i.e., NJst) methods. Each subsampling analysis was repeated 10 times. The color of a square represents the proportion of samples for which the estimated species trees were significantly incongruent (i.e., containing a conflict branch with bootstrap support value  70) with the species tree built from the full data set.
70) with the species tree built from the full data set.
Supplementary Material
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.7q6q3s0.
Funding
This research was supported by National Science Foundation grant DEB 1355343 (EAR 1355292) to S.V.E and National Institutes of Health R01AI093856 to L.L. The publication fees for this article were covered by a grant from the Wetmore Colles Fund of the Museum of Comparative Zoology, Harvard University.
References
- Abadi S., Azouri D., Pupko T., Mayrose I.. 2019. Model selection may not be a mandatory step for phylogeny reconstruction. Nat. Commun. 10:934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aitken A.L., Clarke D.J., McKenna D.D., Shin S., Haddad S., Lemmon A.R., Moriarty Lemmon E., Farrell B.D., Marvaldi A.E., Oberprieler R.G.. 2017. Phylogenomic data yield new and robust insights into the phylogeny and evolution of weevils. Mol. Biol. Evol. 35:823–836. [DOI] [PubMed] [Google Scholar]
- Arcila D., Orti G., Vari R., Armbruster J.W., Stiassny M.L.J., Ko K.D., Sabaj M.H., Lundberg J., Revell L.J., Betancur R.R.. 2017. Genome-wide interrogation advances resolution of recalcitrant groups in the tree of life. Nat. Ecol. Evol. 1:20. [DOI] [PubMed] [Google Scholar]
- Bastide P., Solis-Lemus C., Kriebel R., William Sparks K., Ane C.. 2018. Phylogenetic comparative methods on phylogenetic networks with reticulations. Syst. Biol. 67:800–820. [DOI] [PubMed] [Google Scholar]
- Blaimer B.B., Mawdsley J.R., Brady S.G.. 2018a. Multiple origins of sexual dichromatism and aposematism within large carpenter bees. Evolution. 72:1874–1889. [DOI] [PubMed] [Google Scholar]
- Blaimer B.B., Ward P.S., Schultz T.R., Fisher B.L., Brady S.G.. 2018b. Paleotropical diversification dominates the evolution of the hyperdiverse ant tribe crematogastrini (Hymenoptera: Formicidae). Insect Syst. Diversity. 2:3. [Google Scholar]
- Blair C., Ane C.. 2019. Phylogenetic trees and networks can serve as powerful and complementary approaches for analysis of genomic data. Syst. Biol. doi: 10.1093/sysbio/syz056. [DOI] [PubMed] [Google Scholar]
- Blom M.P.K., Bragg J.G., Potter S., Moritz C.. 2017. Accounting for uncertainty in gene tree estimation: summary-coalescent species tree inference in a challenging radiation of Australian lizards. Syst. Biol. 66:352–366. [DOI] [PubMed] [Google Scholar]
- Bogarín D., Pérez-Escobar O.A., Groenenberg D., Holland S.D., Karremans A.P., Lemmon E.M., Lemmon A.R., Pupulin F., Smets E., Gravendeel B.. 2018. Anchored hybrid enrichment generated nuclear, plastid and mitochondrial markers resolve the Lepanthes horrida (Orchidaceae: Pleurothallidinae) species complex. Mol. Phylogenet. Evol. 129:27–47. [DOI] [PubMed] [Google Scholar]
- Bravo G.A., Antonelli A., Bacon C.D., Bartoszek K., Blom M.P.K., Huynh S., Jones G., Knowles L.L., Lamichhaney S., Marcussen T., Morlon H., Nakhleh L.K., Oxelman B., Pfeil B., Schliep A., Wahlberg N., Werneck F.P., Wiedenhoeft J., Willows-Munro S., Edwards S.V.. 2019. Embracing heterogeneity: coalescing the tree of life and the future of phylogenomics. PeerJ. 7:e6399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown J.M., Thomson R.C.. 2017. Bayes factors unmask highly variable information content, bias, and extreme influence in phylogenomic analyses. Syst. Biol. 66:517–530. [DOI] [PubMed] [Google Scholar]
- Brown J.M., Thomson R.C.. 2018. Evaluating model performance in evolutionary biology. Annu. Rev. Ecol. Evol. Syst. 49:95–114. [Google Scholar]
- Burbrink F.T., Gehara M.. 2018. The biogeography of deep time phylogenetic reticulation. Syst. Biol. 67:743–744. [DOI] [PubMed] [Google Scholar]
- Chen W., Kenney T., Bielawski J., Gu H.. 2019. Testing adequacy for DNA substitution models. BMC Bioinformatics. 20:349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui R., Schumer M., Kruesi K., Walter R., Andolfatto P., Rosenthal G.G.. 2013. Phylogenomics reveals extensive reticulate evolution in xiphophorus fishes. Evolution. 67:2166–2179. [DOI] [PubMed] [Google Scholar]
- Edwards S.V. 2009. Is a new and general theory of molecular systematics emerging? Evolution. 63:1–19. [DOI] [PubMed] [Google Scholar]
- Edwards S.V. 2016. Phylogenomic subsampling: a brief review. Zool. Scr. 45:63–74. [Google Scholar]
- Edwards S.V., Liu L., Pearl D.K.. 2007. High-resolution species trees without concatenation. Proc. Natl. Acad. Sci. USA. 104:5936–5941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards S.V., Xi Z.X., Janke A., Faircloth B.C., McCormack J.E., Glenn T.C., Zhong B.J., Wu S.Y., Lemmon E.M., Lemmon A.R., Leache A.D., Liu L., Davis C.C.. 2016. Implementing and testing the multispecies coalescent model: a valuable paradigm for phylogenomics. Mol. Phylogenet. Evol. 94:447–462. [DOI] [PubMed] [Google Scholar]
- Espeland M., Breinholt J., Willmott K.R., Warren A.D., Vila R., Toussaint E.F.A., Maunsell S.C., Aduse-Poku K., Talavera G., Eastwood R., Jarzyna M.A., Guralnick R., Lohman D.J., Pierce N.E., Kawahara A.Y.. 2018. A comprehensive and dated phylogenomic analysis of butterflies. Curr. Biol. 28:770–778.e775. [DOI] [PubMed] [Google Scholar]
- Gatesy J., Sloan D.B., Warren J.M., Baker R.H., Simmons M.P., Springer M.S.. 2019. Partitioned coalescence support reveals biases in species-tree methods and detects gene trees that determine phylogenomic conflicts. Mol. Phylogenet. Evol. 139:106539. [DOI] [PubMed] [Google Scholar]
- Gatesy J., Springer M.S.. 2014. Phylogenetic analysis at deep timescales: unreliable gene trees, bypassed hidden support, and the coalescence/concatalescence conundrum. Mol. Phylogenet. Evol. 80:231–266. [DOI] [PubMed] [Google Scholar]
- Giarla T.C., Esselstyn J.A.. 2015. The challenges of resolving a rapid, recent radiation: empirical and simulated phylogenomics of Philippine shrews. Syst. Biol. 64:727–740. [DOI] [PubMed] [Google Scholar]
- Goldman N. 1993. Statistical tests of models of DNA substitution. J. Mol. Evol. 36:182–198. [DOI] [PubMed] [Google Scholar]
- Heled J., Drummond A.J.. 2010. Bayesian inference of species trees from multilocus data. Mol. Biol. Evol. 27:570–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey J. 2010. Isolation with migration models for more than two populations. Mol. Biol. Evol. 27:905–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hosner P., Braun E., Kimball R.. 2016. Rapid and recent diversification of curassows, guans, and chachalacas (Galliformes: Cracidae) out of Mesoamerica: phylogeny inferred from mitochondrial, intron, and ultraconserved element sequences. Mol. Phylogenet. Evol. 102:320–330. [DOI] [PubMed] [Google Scholar]
- Jackson N.D., Morales A.E., Carstens B.C., O’Meara B.C.. 2017. Phrapl: phylogeographic inference using approximate likelihoods. Syst. Biol. 66:1045–1053. [DOI] [PubMed] [Google Scholar]
- Jhwueng D.C. 2013. Assessing the goodness of fit of phylogenetic comparative methods: a meta-analysis and simulation study. PLoS One. 8:e67001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jhwueng D.C., Huzurbazar S., O’Meara B.C., Liu L.. 2014. Investigating the performance of AIC in selecting phylogenetic models. Stat. Appl. Genet. Mol. Biol. 13:459–475. [DOI] [PubMed] [Google Scholar]
- Kass R.E., Raftery A.E.. 1995. Bayes factors. J. Am. Stat. Assoc. 90:773–795. [Google Scholar]
- Kubatko L.S. 2009. Identifying hybridization events in the presence of coalescence via model selection. Syst. Biol. 58:478–488. [DOI] [PubMed] [Google Scholar]
- Kubatko L.S., Degnan J.H.. 2007. Inconsistency of phylogenetic estimates from concatenated data under coalescence. Syst. Biol. 56:17–24. [DOI] [PubMed] [Google Scholar]
- Lax G., Eglit Y., Eme L., Bertrand E.M., Roger A.J., Simpson A.G.B.. 2018. Hemimastigophora is a novel supra-kingdom-level lineage of eukaryotes. Nature. 564:410–414. [DOI] [PubMed] [Google Scholar]
- Leache A.D. 2009. Species tree discordance traces to phylogeographic clade boundaries in North American fence lizards (Sceloporus). Syst. Biol. 58:547–559. [DOI] [PubMed] [Google Scholar]
- Lewis P.O., Xie W.G., Chen M.H., Fan Y., Kuo L.. 2014. Posterior predictive Bayesian phylogenetic model selection. Syst. Biol. 63:309–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu L. 2008. Best: Bayesian estimation of species trees under the coalescent model. Bioinformatics. 24:2542–2543. [DOI] [PubMed] [Google Scholar]
- Liu L., Pearl D.K.. 2007. Species trees from gene trees: reconstructing Bayesian posterior distributions of a species phylogeny using estimated gene tree distributions. Syst. Biol. 56:504–514. [DOI] [PubMed] [Google Scholar]
- Liu L., Wu S.Y., Yu L.L.. 2015a. Coalescent methods for estimating species trees from phylogenomic data. J. Syst. Evol. 53:380–390. [Google Scholar]
- Liu L., Xi Z., Davis C.C.. 2015b. Coalescent methods are robust to the simultaneous effects of long branches and incomplete lineage sorting. Mol. Biol. Evol. 32:791–805. [DOI] [PubMed] [Google Scholar]
- Liu L., Yu L.. 2010. Phybase: an R package for species tree analysis. Bioinformatics. 26:962–963. [DOI] [PubMed] [Google Scholar]
- Liu L., Yu L.. 2011. Estimating species trees from unrooted gene trees. Syst. Biol. 60:661–667. [DOI] [PubMed] [Google Scholar]
- Liu L., Yu L., Edwards S.V.. 2010. A maximum pseudo-likelihood approach for estimating species trees under the coalescent model. BMC Evol. Biol. 10:302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu L., Zhang J., Rheindt F.E., Lei F., Qu Y., Wang Y., Zhang Y., Sullivan C., Nie W., Wang J., Yang F., Chen J., Edwards S.V., Meng J., Wu S.. 2017. Genomic evidence reveals a radiation of placental mammals uninterrupted by the KPg boundary. Proc. Natl. Acad. Sci. USA. 114:E7282–E7290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Locke S.A., Van Dam A., Caffara M., Pinto H.A., López-Hernández D., Blanar C.A.. 2018. Validity of the diplostomoidea and diplostomida (digenea, platyhelminthes) upheld in phylogenomic analysis. Int. J. Parasitol. 48:1043–1059. [DOI] [PubMed] [Google Scholar]
- MacGuigan D.J., Near T.J.. 2018. Phylogenomic signatures of ancient introgression in a rogue lineage of darters (Teleostei: Percidae). Syst. Biol. 68:329–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maddison W.P. 1997. Gene trees in species trees. Syst. Biol. 46:523–536. [Google Scholar]
- McGee M.D., Faircloth B.C., Borstein S.R., Zheng J., Darrin Hulsey C., Wainwright P.C., Alfaro M.E.. 2016. Replicated divergence in cichlid radiations mirrors a major vertebrate innovation. Proc. Biol. Sci. 283:1822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLean B.S., Bell K.C., Allen J.M., Helgen K.M., Cook J.A.. 2019. Impacts of inference method and data set filtering on phylogenomic resolution in a rapid radiation of ground squirrels (Xerinae: Marmotini). Syst. Biol. 68:298–316. [DOI] [PubMed] [Google Scholar]
- McVay J.V., Carstens B.. 2013. Phylogenetic model choice: justifying a species tree or concatenation analysis. J. Phylogenet. Evol. Biol. 1:114. [Google Scholar]
- Meiklejohn K.A., Braun E.L., Kimball R.T., Faircloth B.C., Glenn T.C.. 2016. Analysis of a rapid evolutionary radiation using ultraconserved elements: evidence for a bias in some multispecies coalescent methods. Syst. Biol. 65:612–627. [DOI] [PubMed] [Google Scholar]
- Moret B.M.E., Nakhleh L., Warnow T., Linder C.R., Tholse A., Padolina A., Sun J., Timme R.. 2004. Phylogenetic networks: modeling, reconstructibility, and accuracy. IEEE/ACM Trans. Comput. Biol. Bioinform. 1:13–23. [DOI] [PubMed] [Google Scholar]
- Nute M., Chou J., Molloy E.K., Warnow T.. 2018. The performance of coalescent-based species tree estimation methods under models of missing data. BMC Genomics. 19:286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Hara T.D., Hugall A.F., Cisternas P.A., Boissin E., Bribiesca-Contreras G., Sellanes J., Paulay G., Byrne M.. 2019. Phylogenomics, life history and morphological evolution of ophiocomid brittlestars. Mol. Phylogenet. Evol. 130:67–80. [DOI] [PubMed] [Google Scholar]
- Page R.D.M. 1998. Genetree: comparing gene and species phylogenies using reconciled trees. Bioinformatics. 14:819–820. [DOI] [PubMed] [Google Scholar]
- Paradis E., Schliep K.. 2019. Ape 5.0: an environment for modern phylogenetics and evolutionary analyses in r. Bioinformatics. 35:526–528. [DOI] [PubMed] [Google Scholar]
- Prum R.O., Berv J.S., Dornburg A., Field D.J., Townsend J.P., Lemmon E.M., Lemmon A.R.. 2015. A comprehensive phylogeny of birds (Aves) using targeted next-generation DNA sequencing. Nature. 526:569. [DOI] [PubMed] [Google Scholar]
- Rambaut A., Grassly N.C.. 1997. Seq-gen: an application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comput. Appl. Biosci. 13:235–238. [DOI] [PubMed] [Google Scholar]
- Rannala B., Yang Z.H.. 2003. Bayes estimation of species divergence times and ancestral population sizes using DNA sequences from multiple loci. Genetics. 164:1645–1656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala B., Yang Z.H.. 2008. Phylogenetic inference using whole genomes. Annu. Rev. Genom. Hum. Genet. 9:217–231. [DOI] [PubMed] [Google Scholar]
- Reeves J.H. 1992. Heterogeneity in the substitution process of amino-acid sites of proteins coded for by mitochondrial-DNA. J. Mol. Evol. 35:17–31. [DOI] [PubMed] [Google Scholar]
- Reid N.M., Hird S.M., Brown J.M., Pelletier T.A., McVay J.D., Satler J.D., Carstens B.C.. 2014. Poor fit to the multispecies coalescent is widely detectable in empirical data. Syst. Biol. 63:322–333. [DOI] [PubMed] [Google Scholar]
- Richards E.J., Brown J.M., Barley A.J., Chong R.A., Thomson R.C.. 2018. Variation across mitochondrial gene trees provides evidence for systematic error: how much gene tree variation is biological? Syst. Biol. 67:847–860. [DOI] [PubMed] [Google Scholar]
- Robinson D.F., Foulds L.R.. 1981. Comparison of phylogenetic trees. Math. Biol. 53:131–147. [Google Scholar]
- Roch S., Steel M.. 2015. Likelihood-based tree reconstruction on a concatenation of aligned sequence data sets can be statistically inconsistent. Theor. Popul. Biol. 100:56–62. [DOI] [PubMed] [Google Scholar]
- Romiguier J., Ranwez V., Delsuc F., Galtier N., Douzery E.J.. 2013. Less is more in mammalian phylogenomics: at-rich genes minimize tree conflicts and unravel the root of placental mammals. Mol. Biol. Evol. 30:2134–2144. [DOI] [PubMed] [Google Scholar]
- Romiguier J., Roux C.. 2017. Analytical biases associated with GC-content in molecular evolution. Front. Genet. 8:16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sann M., Niehuis O., Peters R.S., Mayer C., Kozlov A., Podsiadlowski L., Bank S., Meusemann K., Misof B., Bleidorn C., Ohl M.. 2018. Phylogenomic analysis of apoidea sheds new light on the sister group of bees. BMC Evol. Biol. 18:71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scornavacca C., Galtier N.. 2017. Incomplete lineage sorting in mammalian phylogenomics. Syst. Biol. 66:112–120. [DOI] [PubMed] [Google Scholar]
- Shen X.X., Hittinger C.T., Rokas A.. 2017. Contentious relationships in phylogenomic studies can be driven by a handful of genes. Nat. Ecol. Evol. 1:126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimodaira H. 2002. An approximately unbiased test of phylogenetic tree selection. Syst. Biol. 51:492–508. [DOI] [PubMed] [Google Scholar]
- Shimodaira H., Hasegawa M.. 1999. Multiple comparisons of log-likelihoods with applications to phylogenetic inference. Mol. Biol. Evol. 16:1114–1116. [Google Scholar]
- Simion P., Philippe H., Baurain D., Jager M., Richter D.J., Di Franco A., Roure B., Satoh N., Quéinnec É., Ereskovsky A., Lapébie P., Corre E., Delsuc F., King N., Wörheide G., Manuel M.. 2017. A large and consistent phylogenomic dataset supports sponges as the sister group to all other animals. Curr. Biol. 27:958–967. [DOI] [PubMed] [Google Scholar]
- Simmons M.P., Gatesy J.. 2015. Coalescence vs. concatenation: sophisticated analyses vs. first principles applied to rooting the angiosperms. Mol. Phylogenet. Evol. 91:98–122. [DOI] [PubMed] [Google Scholar]
- Simmons M.P., Sloan D.B., Gatesy J.. 2016. The effects of subsampling gene trees on coalescent methods applied to ancient divergences. Mol. Phylogenet. Evol. 97:76–89. [DOI] [PubMed] [Google Scholar]
- Song S., Liu L., Edwards S.V., Wu S.. 2012. Resolving conflict in eutherian mammal phylogeny using phylogenomics and the multispecies coalescent model. Proc. Natl. Acad. Sci. USA. 109:14942–14947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Springer M.S., Gatesy J.. 2016. The gene tree delusion. Mol. Phylogenet. Evol. 94:1–33. [DOI] [PubMed] [Google Scholar]
- Stamatakis A. 2014. Raxml version 8: a tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics. 30: 1312–1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Straube N., Li C., Mertzen M., Yuan H., Moritz T.J.B.E.B.. 2018. A phylogenomic approach to reconstruct interrelationships of main clupeocephalan lineages with a critical discussion of morphological apomorphies. BMC Evol. Biol. 18:158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suchard M.A., Lemey P., Baele G., Ayres D.L., Drummond A.J., Rambaut A.. 2018. Bayesian phylogenetic and phylodynamic data integration using beast 1.10. Virus Evol. 4:vey016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavare S. 1986. Some probabilistic and statistical problems in the analysis of DNA sequences. Lectures on Math. Life Sci. 17: 57–86. [Google Scholar]
- Waddell P.J. 2005. Measuring the fit of sequence data to phylogenetic model: allowing for missing data. Mol. Biol. Evol. 22:395–401. [DOI] [PubMed] [Google Scholar]
- Waddell P.J., Ota R., Penny D.. 2009. Measuring fit of sequence data to phylogenetic model: gain of power using marginal tests. J. Mol. Evol. 69:289–299. [DOI] [PubMed] [Google Scholar]
- Walstrom V.W., Klicka J., Spellman G.M.. 2012. Speciation in the white-breasted nuthatch (sitta carolinensis): a multilocus perspective. Mol. Ecol. 21:907–920. [DOI] [PubMed] [Google Scholar]
- Wang Y., Zhou Y., Li L.F., Chen X., Liu Y.T., Ma Z.M., Xu S.H.. 2014. A new method for modeling coalescent processes with recombination. BMC Bioinformatics. 15:273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen D., Yu Y., Nakhleh L.. 2016. Bayesian inference of reticulate phylogenies under the multispecies network coalescent. PLoS Genet. 12:e1006006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whelan N.V., Kocot K.M., Moroz L.L., Halanych K.M.. 2015. Error, signal, and the placement of Ctenophora sister to all other animals. Proc. Natl. Acad. Sci. USA. 112:5773–5778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu S., Edwards S., Liu L.. 2018. Genome-scale DNA sequence data and the evolutionary history of placental mammals. Data Brief. 18:1972–1975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xi Z., Liu L., Davis C.C.. 2016. The impact of missing data on species tree estimation. Mol. Biol. Evol. 33:838–860. [DOI] [PubMed] [Google Scholar]
- Yang Z. 1994. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J. Mol. Evol. 39:306–314. [DOI] [PubMed] [Google Scholar]