Movement Decomposition in the Primary Motor Cortex

Abstract

A complex action can be described as the composition of a set of elementary movements. While both kinematic and dynamic elements have been proposed to compose complex actions, the structure of movement decomposition and its neural representation remain unknown. Here, we examined movement decomposition by modeling the temporal dynamics of neural populations in the primary motor cortex of macaque monkeys performing forelimb reaching movements. Using a hidden Markov model, we found that global transitions in the neural population activity are associated with a consistent segmentation of the behavioral output into acceleration and deceleration epochs with directional selectivity. Single cells exhibited modulation of firing rates between the kinematic epochs, with abrupt changes in spiking activity timed with the identified transitions. These results reveal distinct encoding of acceleration and deceleration phases at the level of M1, and point to a specific pattern of movement decomposition that arises from the underlying neural activity. A similar approach can be used to probe the structure of movement decomposition in different brain regions, possibly controlling different temporal scales, to reveal the hierarchical structure of movement composition.

Introduction

Compositionality and serial processing play a key role in our interaction with the environment. We listen to a speech by effortlessly grouping phonemes into words, and detect objects by grouping points into lines, and lines into shapes. Principles of compositionality are also used in acting on the environment, since writing one’s name or performing a dance move involves the concatenation of several movement elements. Yet, the structure of movement composition and the underlying neural dynamics are not well understood, posing a problem for the analysis of complex movements, as well as for attempts to mimic human movement using artificial devices. Identifying movement segments and their representation in the motor cortex are thus necessary steps towards a complete understanding of the manner by which a goal-directed action is translated into the final output movement (Doeringer and Hogan 1998; d’Avella et al. 2003; Mussa-Ivaldi and Solla 2004; Flash and Hochner 2005; Hatsopoulos et al. 2007; Giszter 2015).

Previous studies have proposed different models for the serial and parallel processing of action composition, both at the kinematic level such as the superposition of short strokes characterized by bell-shaped speed profiles (Abend et al. 1982; Viviani and Terzuolo 1982; Miall et al. 1986; Flash and Henis 1991; Milner 1992; Doeringer and Hogan 1998; Krebs et al. 1999; Hatsopoulos et al. 2007; Polyakov et al. 2009), and at the dynamics level, such as the summation of spatio-temporal patterns of muscle activities (Mussa-Ivaldi et al. 1994; Giszter and Kargo 2000; Kargo and Giszter 2000; d’Avella et al. 2003; Cheung et al. 2005; d’Avella and Bizzi 2005; Overduin et al. 2012, 2015). The proposed compositional elements are hypothesized to be more complex than an instantaneous single muscle activation, and are frequently described as generating temporally extended elements that combine the activities of different muscles and joints. An important step towards supporting this hypothesis was made by studies employing long-duration intracortical microstimulation (ICMS), which demonstrated that transient activation of M1 neurons evoked complex time-dependent movements, involving multiple muscles across one or more joints (Graziano et al. 2002; Overduin et al. 2012).

A dynamical system perspective focusing on the ensemble activity of neural populations offers a framework that may provide a better understanding of the neural processes underlying the observed evoked responses (Abeles et al. 1995; Churchland et al. 2012; Shenoy et al. 2013). In this framework, the ensemble activity in the motor cortex is thought to facilitate the executed movement by shifting from a state of spontaneous activity to a state associated with the intended action. Once the population reaches the intended state, or pattern of activity, the ensemble dynamics elicit the generation of the corresponding movement. By tracing the population dynamics, previous studies have identified transitions between epochs of movement preparation and execution, and have distinguished between preparatory states associated with different intended actions (Abeles et al. 1995; Kemere et al. 2008; Churchland et al. 2010; Afshar et al. 2011; Petreska et al. 2011).

Here, we sought to identify the temporal structure of movement decomposition by targeting the dynamics of the associated neural population activity. We hypothesized that transitions in the population activity may not only distinguish between global epochs of movement preparation and execution, but further reveal transitions between movement segments, allowing an estimation of the composing elements directly from the underlying neural activity. To identify state transitions in the population activity, we modeled the firing patterns of dozens of neurons in M1 of non-human primates, recorded during the execution of arm movements in a random target pursuit (RTP) task and in a center-out reaching task, using a hidden Markov model (HMM). The underlying assumption of an HMM is that a time-evolving low-dimensional hidden state (e.g., neural state) is indirectly observed through a noisy signal (e.g., firing of neurons) (Rabiner 1989; Abeles et al. 1995; Kemere et al. 2008; Polyakov et al. 2009; Escola et al. 2011). Modeling the population activity using an HMM enabled us to estimate the structure of movement decomposition solely from the neural activity in M1, in an unsupervised manner, without any assumptions on the encoded movement parameters and without predefining a specific duration for the composing elements. The identified neural segmentation revealed distinct epochs of movement, consistently decomposing the movement into acceleration and deceleration phases executed towards specific directions in the workspace. These findings provide new insights regarding the temporal structure of movement decomposition and its underlying neural representation.

Methods

Behavioral Task

The experiments were performed on two male rhesus macaques (“RJ” and “RS”, ages 9 and 6, respectively). The manner in which the data were collected and handled was previously described in Hatsopoulos et al. (2007), and is further discussed below. Subjects were trained to move a cursor appearing on a horizontal screen above the monkey’s hand location toward targets projected onto the screen. The monkey’s arm was attached to a two-joint exoskeletal robotic arm (BKIN Technologies, Inc.). The shoulder joint was abducted by 90°, such that the shoulder and elbow flexion and extension movements were made in the horizontal plane. The shoulder and elbow joint angles were sampled at 500 Hz by the robotic arm’s motor encoders. The X and Y positions of the hand were computed using forward kinematics calculations.

Random Target Pursuit Task

The monkeys performed a random target pursuit (RTP) task, in which a sequence of 7 targets appeared on the projection surface (Fig. 1A). At any one time, a single target appeared at a pseudo-random location in the workspace, and the monkey was required to move toward it. As soon as the cursor reached the target, the target disappeared and a new target appeared at a new randomly selected location. After reaching the seventh target the monkey was rewarded with a drop of water. We only analyzed successful trials, in which the monkey reached 7 targets in a reasonable time (≤8 s) and did not stop for more than 500 ms, and discarded trials in which X and Y were outside the workspace boundaries or trials in which the monkey’s speed exceeded the average speed +3 SD, to avoid excessive noise that may reflect erroneous measurements.

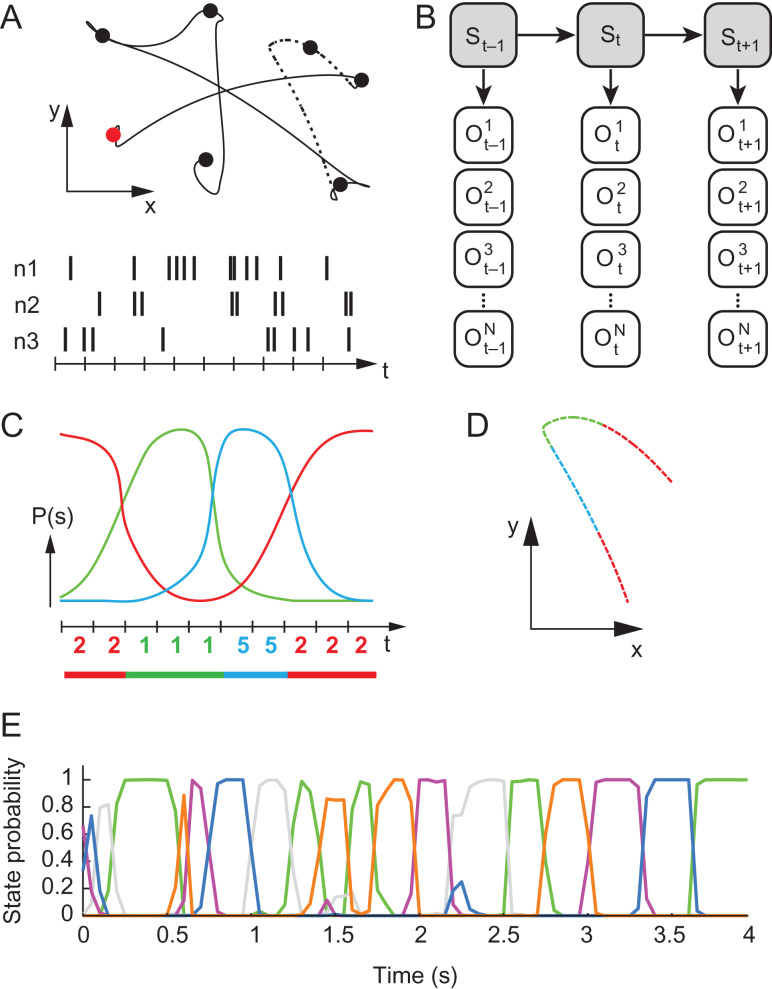
Figure 1.

Experimental paradigm and illustration of HMM analysis. (A) Top: An example of a single behavioral trial in the RTP task. In each successful trial the monkey passed through 7 targets that appeared sequentially at pseudo-random locations in the workspace. Filled circles represent the target locations, first target is colored in red. Bottom: illustration of spike trains for 3 neurons, recorded during the behavioral task. (B) HMM modeling and training: $O_t^n$ is a variable corresponding to the observed spike-count within time bin $t$, for the nth neuron. Observables at each time point are assumed to be dependent on a hidden state $S_t$, according to the distribution $P(O^n\mathit{|S})$. The dynamics of the states is governed by the transition probability $P(S_{t+1}|S_t$). Training of the model yields an estimation of these distributions from the observed spike trains. (C) Decoding: Using the trained model, the sequence of hidden states is inferred for an independent test trial by calculating the probability for each hidden state at each time-bin for a given set of spike trains (each color represents a different state). A deterministic sequence of states is then constructed by associating each time bin with the most probable state at that time point (color-coded digits represent the sequence of decoded hidden states). Consecutive bins that are associated with the same state make up a segment (segmented line at the bottom). (D) Movement segmentation: The resulting neural segmentation is used to segment the behavioral data, taking into account a lag of 100 ms. The line trace shows a section of the movement path corresponding to the dashed line in A-top, colored according to the illustrated segmentation in C. (E) Example of the state probabilities assessed for a single RTP trial. Each color represents a single neural state. Note the dominance of a single state in most time points and the sharp transitions between dominant states. Data from RJ.

Center-out Task

We also analyzed recordings from a center-out task, performed by monkey RS, which involved movements from a center target to one of 8 peripherally positioned targets (7 cm distance). On each trial, one of the 8 targets was pseudorandomly selected. The task consisted of two epochs: (1) a fixed instruction period of 1000 ms during which the monkey was required to hold its hand over the center target, and one of the 8 peripherally positioned final targets appeared, and (2) a “go” period during which the target began to blink, informing the monkey to begin moving to the target. As we were interested in the neural activity underlying movement execution, we analyzed the neural activation starting from the “go” signal until 100 ms past the point where the speed decreased below 15% of the maximal speed of each trial.

All of the surgical and behavioral procedures were approved by the University of Chicago Institutional Animal Care and Use Committee and conform to the principles outlined in the Guide for the Care and Use of Laboratory Animals (NIH publication no. 86-23, revised 1985).

Neural Data Acquisition

A silicon-based electrode array composed of 100 electrodes (1.0 mm electrode length; 400 μm inter-electrode separation) was implanted in the arm area of the primary motor cortex (M1) of each monkey. During a recording session, signals from up to 96 electrodes were amplified (gain, 5000), bandpass filtered between 0.3 Hz and 7.5 kHz, and recorded digitally (14-bit) at 30 kHz per channel using a Cerebus acquisition system (BlackRock Microsystems, Salt Lake City, UT). Only waveforms (1.6 ms in duration) that crossed a threshold were stored and spike-sorted using Offline Sorter (Plexon, Inc., Dallas, TX). A single recording session from each monkey was analyzed in this study from the RTP task, with 54 and 100 simultaneously recorded units from M1 of RJ and RS, respectively, and a single recording session from the center-out task with 141 units from M1 of RS.

Neural Data Segmentation Using a Hidden Markov Model

Data Preprocessing

Spikes were binned by summing the number of spikes of each single unit within non-overlapping 50 ms windows. We refer to the ensemble activation at each time point as an “activation pattern”, denoted as: ${\mathit{O}}_t=(O_t^1,O_t^2,\mathrm{\dots },O_t^N)$ where $O_t^n$ is an integer variable, corresponding to the number of spikes observed in the $n^{\mathit{th}}$ neuron at time-step $t$, and $N$ is the number of neurons. For each recording session, about 75% of the trials were defined as a training set (251/334 trials for RJ in the RTP task, 569/758 for RS in the RTP task, 293/391 for RS in the center-out task), whereas the rest of the trials were used as an independent test set.

Hidden Markov Model (HMM)

Recorded spike trains were modeled using a hidden Markov model, a method frequently used in speech and hand gesture recognition (Rabiner 1989). An HMM describes a system that transitions between distinct states, related by a Markov process. The states are hidden and can only be observed through the observations that are a probabilistic process of the hidden states. Here, the model regards the recorded spike trains as observations, dependent on the hidden states that are assumed to reflect global changes in cortical activity (Abeles et al. 1995). Formally, assuming there are $M$ possible states $S_t\in \{\mathrm{1,\; 2},\mathrm{\dots },\mathit{M}\}$, the Markovian property implies that the hidden process is fully described by the transition probabilities $P\left(S_t=i\right|S_{t-1}=j)=A_{\mathit{ji}}$ [$M\times M$ matrix], and an initial distribution $P\left(S_1=i\right)={\pi }_i$ [column vector of length $M$]. The dependence between the hidden states and the observable output (emissions) is captured by a conditional distribution, $P\left({\mathit{O}}_t\right|S_t=i)=B_i\left({\mathit{O}}_t\right)$, where ${\left\{\mathit{O}\right\}\equiv \left\{{\mathit{O}}_t\right\}}_{t=1}^T$ represents the sequence of observations. In this work, we employed a homogeneous discrete time Markov chain, and defined the emissions as an ensemble of $N$ emission-units ${\mathit{O}}_t=\left(O_t^1,\mathrm{\dots },O_t^N\right)$ that represent the $N$ recorded neurons (Fig. 1B). We assume that emission units (neurons) are independent given a state, and that each unit may obtain one of $k=\mathrm{0,\; 1},\mathrm{\dots },(K-1)$ possible values (i.e., spike-counts). Namely, each unit $\left(n\right)$ is described by its own distribution $P\left(O_t^n=k\right|S_t=i)=B_i^n\left(k\right)$ [$M\times K$ matrix], and the full emission probability is captured by matrix $\mathit{B}$ such that $B_i\left({\mathit{O}}_t\right)=\prod _{\mathrm{n}=1}^{\mathrm{N}}{B}_i^n\left(O_t^n\right).$ Thus, an HMM is fully described by the set of distributions $\lambda =\{\pi ,A,\mathit{B}\}$. Note that in this implementation of HMM the distributions are non-parametric, liberating the model from any assumptions regarding the behavior of individual units.

Training & Decoding

A separate HMM was trained for each of the 3 analyzed recording sessions using the observed spike trains from trials in the training sets. Training of the models was done using the Baum–Welch algorithm, an iterative expectation-maximization algorithm for finding the maximum likelihood estimate of the model parameters given the sequence of observations, widely used for HMM training (Baum and Petrie 1966). The Baum–Welch algorithm makes use of the forward–backward procedure, which yields the likelihood of the observation sequence $\{\mathit{O}\}$ given the model parameters $\lambda$: $P(\{\mathit{O}\left\}\mathit{|}\lambda \right)$. The standard forward–backward algorithm is designed for models with a single emission node, i.e., a conditional distribution of a single unit $B_i^n\left(O_t^n\right)$. To account for multiple emission nodes we replaced this distribution with the full emission distribution $B_i\left({\mathit{O}}_{\mathit{t}}\right)$. A known drawback of the Baum–Welch algorithm is its sensitivity to initial conditions, especially for models with a large number of parameters such as in our case. To address this issue the algorithm was incorporated in a simulated-annealing regime (Paul 1985). On each iteration, a small perturbation of the parameters was generated and the new parameters were considered as candidates for replacing the current parameters. The perturbation was random, with a tendency to increase the transition matrix’s diagonal values, reflecting a preference for “persistent” states and smooth dynamics. Specifically, a perturbation was generated by randomly selecting half of the matrix rows, and for each selected row i, choosing a single column j, according to the distribution $P\left(j\right)$ s.t. $P\left(j=i\right)=0.5,\mathit{P}\left(j\ne i\right)=0.5/(M-1)$. Transition probabilities in the resulting matrix indices were then each increased by a random factor, followed by a normalization of the rest of the transition probabilities in the same row, such that each row will still sum to 1. Next, the difference between the log-likelihoods of the original and the candidate parameters was computed: $\mathrm{\Delta }\mathit{LL}=\mathit{LL}\left(\lambda \right)-\mathit{LL}\left({\lambda }_{\mathrm{cand}}\right)$. The candidate parameters were then accepted with probability $P\left(\lambda \leftarrow {\lambda }_{\mathrm{cand}}\right)=\min \left({\mathrm{e}}^{-{\beta }_t\mathrm{\Delta }\mathit{LL}},1\right)$, ${\mathrm{\beta }}_{\mathrm{t}}$ being the inverse of the temperature, governed by the annealing process. The number of states used to construct the models was determined by repeating the process for a range of possible values (2–15 states) and calculating the cross-validated log likelihood calculated on the test set. We also calculated a moderate version of the Akaike information criterion (AIC), penalizing the log likelihood for an increasing number of free parameters in the transition matrix (AIC was calculated as: $\mathrm{AIC}=2K-2\mathit{LL}$, where $K$ is the number of free parameters in the transition matrix and $\mathit{LL}$ is the log-likelihood of the model on the test set). For each monkey, we selected the number of states that maximized the log-likelihood before it reached a plateau, which also corresponded to a similar range of number of states that minimized the AIC measure (see Supplementary Fig. 6). For the center-out session, the number of states was taken to be the same as obtained for RS in the RTP session, which resulted in 7 meaningful states and one empty state (training the model on a higher number of states resulted in further empty states). It should be emphasized that the exact number of obtained states is not thought to reflect a closed set of elementary building blocks, and may vary depending on the nature of the behavioral task, while the obtained segmentation is assumed to reflect global changes in the dynamics of the population activity underlying the execution of movement.

The trained models were subsequently used to infer the sequence of hidden states of trials in the test sets (“decoding”). We employed the forward–backward algorithm to estimate the probability that the system was at a certain hidden state at each time-bin given the observed spike trains and the model parameters: $P(S_t|\left\{\mathit{O}\right\},\lambda )$. To obtain a deterministic sequence of states, each bin was associated with the single most probable state at that bin, $s_t={\mathrm{argmax}}_{i}P(S_t=\mathit{i|}\mathbf{\{O\}},\lambda )$. A time-bin at which a state change occurred ($t$ such that $s_t\ne s_{t-1}$) defined the beginning of a new neural segment, each such segment had a single hidden state associated with it (Fig. 1C). Bins that were associated with a state that lasted for only one time step or had a probability lower than 60% were discarded and replaced by the last state (this corresponded to <10% of the bins in each dataset; these bins were not included in the analyses performed on the extracted segments).

Movement Segmentation

Kinematic data were smoothed via a fourth-order Butterworth low pass filter with 6 Hz cut-off. To examine movement decomposition, the kinematic data was then segmented according to the obtained neural segmentation, and each single neural segment defined a corresponding movement segment, taking into account a lag of 100 ms between the neural activation and the kinematic output (Fig. 1D) (Schwartz 1994; Paninski, Fellows, et al. 2004). Note that the entire training of the HMM and the subsequent decoding of the neural states did not depend on the chosen lag.

Assessing Behavioral Relevance of Neural Segmentation in the RTP Task

We first assessed whether the neural segmentation parsed the kinematic output in behaviorally relevant points. Using the neural segmentation to parse the movements executed during the RTP task yielded a decomposition that coincided with specific time points of the kinematic output. Namely, neural state transitions occurred in close proximity to minima and maxima points of the tangential velocity of the end-effector. To test whether the transition points between neural states indeed corresponded to speed extrema in the movement, we first computed the correlation between the number of neural state transitions and the number of speed extrema across trials. The resulting correlation values were compared to null distributions of correlation values, created by shuffling the labels of the trials 10³ times. In each shuffle, we calculated the correlation on random pairings between the number of speed extrema and the number of state transitions. As the number of state transitions and speed extrema may be affected by the length of the trial, we next examined whether the time points of neural state transitions could predict the time points of speed extrema. This was accomplished by calculating precision and recall measurements, which are a better estimate of model predictions in the case of sparse events (instead of the often-used ROC curves), as is the case of speed extrema in a whole trial. To calculate these measurements, we first paired points of speed extrema and points of state transitions in each trial using a cost-based metric originally proposed by Victor and Purpura (1996) to compare between two spike trains. In short, this method aligns the time points of two vectors by minimizing an estimated cost. This includes a cost of 1 for each instance which should be inserted or deleted, and a cost of q*t for each shift in time of a single instance. Two time points are coupled together only if the cost of the time shift between them is smaller than the cost of insertion and deletion. We used q = 20, corresponding to two time bins, i.e., 100 ms. The mean absolute distance between matched points was 0.039 s ± 0.026 SD for RJ and 0.041 s ± 0.026 SD for RS, and the distributions of signed distances were centered on zero, suggesting that there was no bias between the time points of neural state transitions and the speed extrema. This was confirmed by using a lag of 50 ms or 150 ms, which gave a higher mean absolute distance and skewed distributions in either direction (Supplementary Fig. 1). Note that the timing of state transitions is limited by the resolution of binned spikes. We regarded matched pairs as true positives, any state transition that was not matched to a speed extremum was considered as a false positive, and any non-matched speed extremum was considered as a false negative. For each trial we then calculated the precision as $\frac{\mathrm{\#\; true\; positives}}{\mathrm{\#\; true\; positives}+\mathrm{\#\; false\; positives}}$, and the recall as $\frac{\mathrm{\#\; true\; positives}}{\mathrm{\#\; true\; positives}+\mathrm{\#\; false\; negatives}}$. In a perfect prediction, both the precision and recall would be equal to one, suggesting that the state transitions predicted all speed extrema, and did not falsely predict any event. We compared these resulting measurements with null distributions, created by placing the neural state transitions at random times within the trial, calculating the above-mentioned measures, and repeating the process 10³ times (possible times were taken according to the resolution of the binned spikes).

Next, we examined whether the obtained neural states were characterized by specific kinematic features. Specifically, we extracted the movement segments corresponding to each of the states and calculated different movement parameters for each of the segments, including the mean direction, speed, tangential acceleration, and Euclidean length. We then performed one-way ANOVA for the different kinematic parameters to test for a consistent difference between the segments corresponding to the different states. We also ran a sign test for the mean acceleration within each state, examining the distribution of average acceleration values of the segments corresponding to each state. For visualization purposes, speed profiles of the segments corresponding to each state were normalized both in time and in amplitude, and resampled to enable the calculation of the average speed profile across segments.

Segmentation of Center-out Reaching Movements

We conducted similar analyses on the center-out dataset to characterize the relation between the obtained neural segmentation and the kinematic output. Here too, the identified transitions between neural states occurred in proximity to extrema points of the speed profile. To verify this observation, we calculated the distances between time points of peak speed in the reaching movements and the nearest neural state transition. We also assessed the number of segments obtained during the initial bell-shaped speed profile, between the point at which the speed first exceeded 15% of maximal speed in that trial and the first minimum point following peak speed, to specifically address the first speed bump and avoid possible additional submovements near the target.

Simulations of Instantaneous Encoding of Kinematic Parameters

To test whether the obtained segmentation could emerge from previously proposed models of instantaneous encoding of kinematic parameters (Georgopoulos et al. 1982; Schwartz and Moran 2000), we used the center-out dataset and simulated populations of spiking neurons tuned for velocity and acceleration. We tested 6 models that incorporated tuning for: (1) movement direction; (2) movement direction gain modulated by speed; (3) direction of the acceleration vector; (4) direction of the acceleration vector gain modulated by the magnitude of the acceleration vector; (5) both movement direction and direction of the acceleration vector; or (6) both movement direction and direction of the acceleration vector, each gain modulated by the magnitude of the corresponding vector:

1. ${\mathit{fr}}_i\left(t-\tau \right)={B_0}_i+{B_1}_i\cos \mathrm{}({\theta }_v\left(t\right)-{\theta }_{{\mathit{v\; pd}}_i})$

2. ${{{\mathit{fr}}_i\left(t-\tau \right)=B}_0}_i+{B_1}_i\Vert \vec{v}\left(t\right)\Vert \cos \mathrm{}({\theta }_v\left(t\right)-{\theta }_{{\mathit{v\; pd}}_i})$

3. ${\mathit{fr}}_i\left(t-\tau \right)={B_0}_i+{B_1}_i\cos \mathrm{}({\theta }_a\left(t\right)-{\theta }_{{\mathit{apd}}_i})$

4. ${\mathit{fr}}_i\left(t-\tau \right)={B_0}_i+{B_1}_i\Vert \vec{a}\left(t\right)\Vert \cos \mathrm{}({\theta }_a\left(t\right)-{\theta }_{{\mathit{apd}}_i})$

5. ${\mathit{fr}}_i\left(t-\tau \right)={B_0}_i+{B_1}_i\cos \mathrm{}({\theta }_v\left(t\right)-{\theta }_{{\mathit{v\; pd}}_i})+{B_2}_i\cos \mathrm{}({\theta }_a\left(t\right)-{\theta }_{{\mathit{apd}}_i})$

6. ${\mathit{fr}}_i\left(t-\tau \right)={B_0}_i+{B_1}_i\Vert \vec{v}\left(t\right)\Vert \cos \mathrm{}({\theta }_v\left(t\right)-{\theta }_{{\mathit{v\; pd}}_i})+{B_2}_i\Vert \vec{a}\left(t\right)\Vert \cos \mathrm{}({\theta }_a\left(t\right)-{\theta }_{{\mathit{apd}}_i})$

where ${\mathit{fr}}_i$ is the instantaneous firing rate of neuron $i$, $\tau$ is the time lag between neural activity and kinematic output (taken to be 100 ms), ${B_0}_i$ is the baseline firing rate, ${B_1}_i$ and ${B_2}_i$ are modulation depths, $\Vert \vec{v}\left(t\right)\Vert$ and $\Vert \vec{a}\left(t\right)\Vert$ represent the magnitude of the velocity and acceleration vectors, respectively, ${\theta }_v$ and ${\theta }_a$ are the directions of the velocity and acceleration vectors, and ${\theta }_{{\mathit{v\; pd}}_i}$ and ${\theta }_{{\mathit{apd}}_i}$ are the preferred velocity and acceleration angles of neuron $i$. For each simulation, we first extracted the corresponding $\beta$ values and preferred directions from the actual data by performing a regression analysis per each neuron. Next, we simulated the spike trains of each neuron $i$ according to the recorded kinematics (with $\mathit{dt}=2\mathrm{ms}$). For each time step a random threshold $x_{\mathit{th}}$ was chosen from a uniform distribution, and compared to the estimated probability of a spike

$$p_i\left(\mathrm{spike}\right)={\mathit{fr}}_i·\mathit{dt}$$

If $p_i\left(\mathrm{spike}\right)>x_{\mathit{th}}$, a spike occurred, otherwise no spike occurred. The simulated units showed similar average firing rates and standard deviations to the actual data. We then used the simulated spike trains as the original recorded ones, and performed training and testing of the HMM as described in the previous sections.

Neural Activity within HMM States

Single Cell Activation and Correspondence to Neural States

We then turned to characterize the neural activity underlying the obtained segmentation. We first assessed the mean firing rate of each neuron per neural state. Mean firing rates were standardized by subtracting the mean and dividing by the standard deviation of each cell. The resulting z-score values were used to examine the modulation of single cells’ firing rates across the obtained states and to evaluate whether each state was characterized by a unique set of active neurons or whether single cells were active in multiple states.

Next, we examined the firing rates of single units at a higher temporal resolution and asked whether a consistent modulation could be observed at time points of transitions between states across multiple cells. To test this, we extracted the time points of transitions between states, for pairs of states that showed a probability higher than 0.05 of transition (i.e., for transitioning from state i to state j, $A_{\mathit{ij}}>0.05$). Then, we took spike trains from each neuron in a 300 ms time window around the extracted transition points using 5 ms bins and smoothed the firing trains using a 15 ms box-car moving average. We aligned the firing patterns to the time of transition, and averaged across the instances to yield a mean firing pattern per neuron per state-pair. For this analysis we used all the trials, including the trials from the training set, in order to average across as many instances as possible. To test whether single cells showed a modulation in their firing patterns that corresponded to the state transition, we fitted a regression tree to each mean firing pattern described above, constrained to a single partition. This yielded a piece-wise constant model that divided the mean firing rate into two sub-divisions at a specific time point, similar to a step function. For each neuron we then took the state-pair transition which showed the highest goodness of fit with the fitted regression tree, and extracted the time point of the corresponding step. Note that such a step may occur at any time point within the 300 ms time window. Examining the time of the obtained steps can suggest whether indeed single cells showed a consistent change in firing rate that corresponded to the time of state transition, and provide an estimate of the percentage of cells that are involved in the transitions obtained from the HMM. As a control, we performed the same analysis on firing patterns aligned to the middle point of each state, such that averaging across multiple instances would still be meaningful (i.e., averaging the neural activity across instances associated with the execution of similar movements). This enabled us to examine whether a consistent modulation at the level of single cells is unique to the time points of state transitions, or whether it could also be found during the states themselves. As a second control, we generated random transitions within each trial according to the distribution of states’ durations, obtained from the original models, and conducted similar analyses to those described above. We repeated this process for 50 iterations, with random transitions generated each time. This enabled us to assess whether similar modulations may occur by chance, when averaging the firing rate of a single neuron across random time points.

Finally, we tested whether a significant modulation occurred in the activities of single cells between epochs of acceleration and deceleration, regardless of the obtained neural segmentation. To accomplish this, we examined spike trains recorded during the center-out task, and summed the number of spikes per neuron that occurred during time-windows of 150 ms before and after the point of peak speed minus a lag of 100 ms, per trial. We then performed a t-test for paired samples for each neuron to test for a significant difference between the acceleration and deceleration epochs.

Population Activity and Collective Neural Dynamics Within States

The neural activity associated with the obtained segmentation was further examined at the population level. As a visual inspection of the population activity is challenging due to the large number of recorded cells, we performed a principal component analysis (PCA) on the firing rates of the recorded neurons and projected the activity patterns onto a low-dimensional space using the first 3 principal components (Cunningham and Yu 2014). This enabled us to visually examine whether the activity patterns associated with each state corresponded to a consistent and unique representation at the population level. The principal components were computed on smoothed neural data, in which the binned activity (using 10 ms bins) of each unit was filtered separately using a Gaussian with 30 ms SD. Further smoothing was only performed for visualization purposes. Although PCA does not take into account any temporal dependencies as the HMM does, the different principal components may reflect certain dependencies between the neurons that may dissociate between the identified states.

Furthermore, the low-dimensional projection enabled us to visually track the evolution of the time-dependent neural activity within each trial and each neural segment. Although the model we used assumes a relatively simple structure, in which the population activity remains constant within a state, this does not have to be the case. Previous studies have shown that different epochs of movement, such as preparation versus execution, identified using an HMM (Abeles et al. 1995; Kemere et al. 2008), encompass further characteristic temporal structure (Afshar et al. 2011; Churchland et al. 2012). Thus, we examined whether each neural state was associated with a characteristic path that was not captured by the HMM. To test this, we computed the pair-wise distances in the high-dimensional space between pairs of segments associated with the same neural state. Specifically, we extracted segments that were at least 150 ms long and linearly resampled each segment to T = 20 uniformly spaced points. Then, we calculated the distance between the $i^{\mathit{th}}$ and $j^{\mathit{th}}$ segments of state $s$ according to: $d_{\mathit{ij}}^s=\sum _{t=1}^T\Vert {\tau }_i^s\left(t\right)-{\tau }_j^s\left(t\right)\Vert$, where $T$ is the number of uniformly spaced points, ${\tau }_i^s$ is a matrix of size $T\times \mathrm{number\; of\; neurons}$ corresponding to the activity patterns associated with segment $\mathit{i}$, and $\Vert ·\Vert$ denotes the $L_2$ norm. The mean distance per state is given by ${\stackrel{\circledR }{d}}^s=\langle d_{\mathit{ij}}^s\rangle$. To compare the obtained average distances to null distributions, we shuffled the binned spike counts of each segment such that any temporal information would be lost, and conducted the same analysis as described above. This was repeated for 500 iterations to create a null distribution per state. If the firing patterns within a neural segment are merely noise within a certain subspace or around an average pattern of activity, two independent segments should not necessarily share a similar neural trajectory, and a temporal shuffle should not affect the distribution of distances calculated between pairs of segments. This enabled us to examine the existence of any further temporal structure in the population activity within the identified states and to better characterize the underlying population activity.

Results

Movement kinematics and the simultaneous activity of neural populations in M1 of two macaque monkeys were recorded during the performance of a random-target pursuit (RTP) task and a center-out reaching task. We segmented the neural activity by identifying sequences of neural states using a hidden Markov model and used the neural segmentation to parse the kinematic output (Fig. 1). This enabled us to examine the structure of movement decomposition solely from the underlying neural activity in an unsupervised manner without imposing assumptions regarding the encoded movement features, the nature of the segmentation, or the duration of the composing elements.

Segmentation of Neural Activity Reveals Distinct Kinematic Epochs in the RTP Task

Decoding the sequences of neural states in the RTP task resulted in neural segments characterized by a single dominant hidden state that lasted for a few time points (mean segment duration 260 ± 140 ms SD and 240 ± 170 ms, for RJ and RS, respectively), with sharp transitions between dominant states marking the beginning of a new neural segment (Fig. 1E).

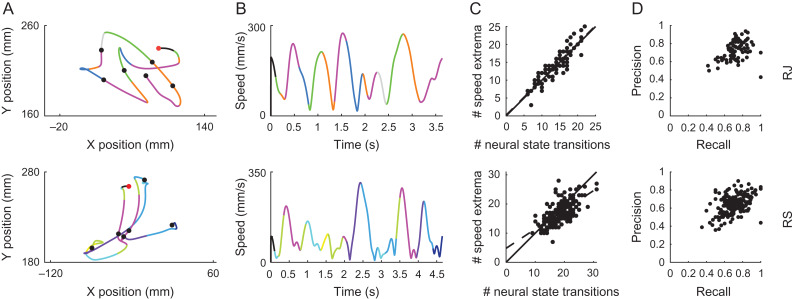
We first assessed the relation between the resulting neural segmentation and the kinematic output by examining whether transitions in the neural population activity segmented the movement in behaviorally relevant points. We found that transitions between the neural states repeatedly occurred in close proximity to points of minima and maxima of the tangential velocity (i.e., speed) of the end effector, segmenting the continuous movement into acceleration and deceleration phases, evident at the level of single trials (Fig. 2A,B). The number of transitions between neural states and the number of movement speed extrema were highly correlated across trials, with a linear fit close to the diagonal line, suggesting that the number of neural state transitions was similar to the number of movement speed extrema within individual trials. These correlation values were significantly higher compared to null distributions, created by shuffling the number of state transitions across trials, such that each trial’s number of speed extrema was paired with a different trial’s number of state transitions (RJ R = 0.89, P < 0.001; RS R = 0.66, P < 0.001, randomization tests, Fig. 2C). We further tested whether the specific timing of the neural state transitions was predictive of points of speed extrema. This was accomplished by pairing time points of neural state transitions with time points of speed extrema (see Methods), and calculating precision $\left(\frac{\mathrm{\#\; true\; positives}}{\mathrm{\#\; true\; positives}+\mathrm{\#\; false\; positives}}\right)$ and recall $\left(\frac{\mathrm{\#\; true\; positi}v\mathit{es}}{\mathrm{\#\; true\; positives}+\mathrm{\#\; false\; negatives}}\right)$ measures. The resulting precision and recall measures were significantly higher than those obtained from null datasets, created by placing the HMM transitions of each trial at random time points within the trial (RJ mean precision from actual dataset – 0.73 ± 0.011 SEM, mean recall – 0.73 ± 0.012 SEM; RS mean precision – 0.64 ± 0.007 SEM, mean recall – 0.7 ± 0.008 SEM, P < 0.001 for both precision and recall measures in both monkeys, randomization tests, Fig. 2D).

Figure 2.

Movement decomposition following neural segmentation in the RTP task. (A) Position data of exemplar trials from the RTP task segmented and colored according to the decoded neural states. Each color represents a single state. Filled circles represent the target locations, first target is colored in red. (B) Corresponding speed profiles, colored as in A. (C) Number of speed extrema versus number of neural state transitions across trials. Each point represents a single RTP trial, dashed line represents the linear regression line, solid line represents the 45° line. (D) Precision versus recall across trials. Each point represents a single trial. Top row - monkey RJ, bottom row - monkey RS.

As there is a strong coupling between instantaneous tangential velocity and path curvature (Abend et al. 1982; Lacquaniti et al. 1983; Flash and Hogan 1985), we assessed whether the obtained neural segmentation specifically occurred at points of high curvature, i.e., at changes of movement direction. As can be seen in Supplementary Figure 2A, neural state transitions that co-occurred with minima points of the speed profile were also associated with curvature maxima. However, neural transitions also occurred along straight segments (i.e., $\mathrm{curvature}\to 0$), at points of speed maxima. Consistently, the number of neural transition points was higher than the number of curvature maxima across trials (Supplementary Fig. 2B), suggesting that global changes of the population dynamics are not solely related to changes in movement direction, but are more tightly coupled to maxima and minima of the tangential velocity.

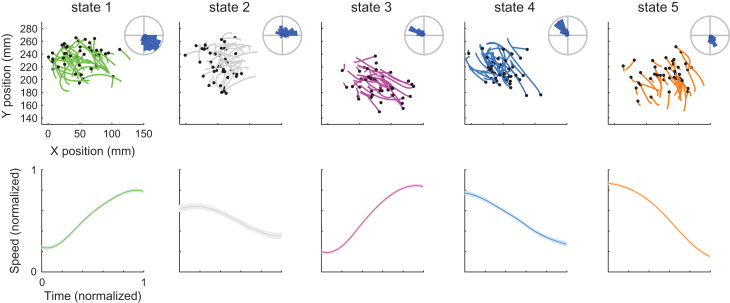
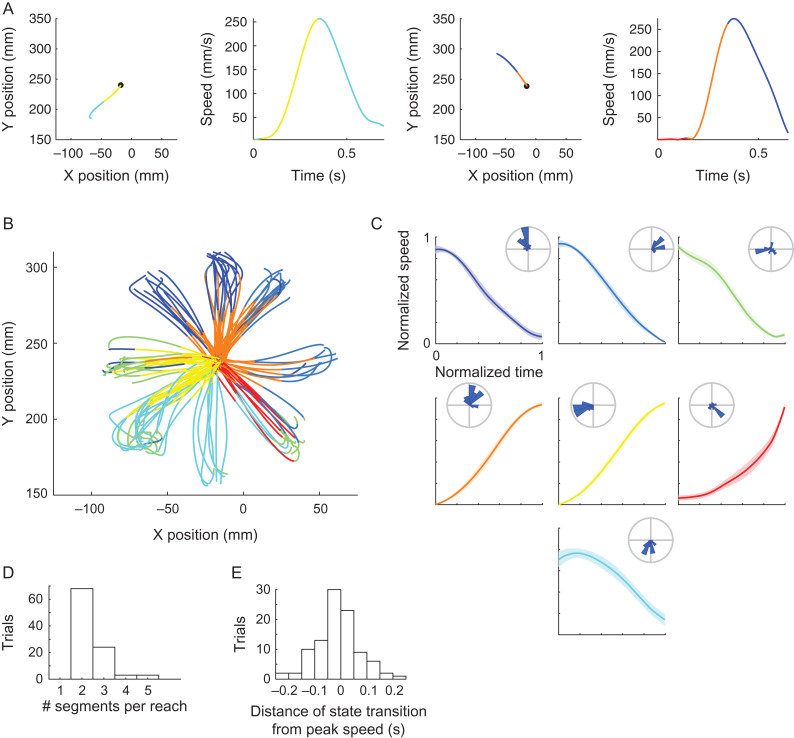
We next examined the movement segments associated with each of the neural states. In both monkeys, each neural state was coupled with either accelerating or decelerating movement segments that occurred between successive speed extrema, executed towards a specific direction within the workspace. Hence, a single neural state corresponded, for example, to accelerating movement segments executed from left to right. The top panels in Figure 3 and Supplementary Figure 3 show the apparent directional selectivity within each state (one-way ANOVA for movement direction RJ – F(4 1225) = 317, P < 0.001; RS F(7 3721) = 264, P < 0.001). The bottom panels in Figure 3 and Supplementary Figure 3 show the mean normalized speed profile across segments for each neural state, emphasizing the accelerating or decelerating shape within each state (one-way ANOVA for mean tangential acceleration across states RJ – F(4 1225) = 172, P < 0.001; RS – F(7 3721) = 309, P < 0.001; sign-test for mean tangential acceleration showed P < 0.001, for all states in both datasets, except for state 3 in RS).

Figure 3.

Directional and acceleration selectivity of neural states in the RTP task. Top – Each panel shows the position of movement segments corresponding to each of the neural states. Each line is a single segment, black dots represent the beginning of the segment. For visualization purposes we only show a random subset of the segments. Radial histograms show the mean directions of all the segments within each state. Bottom – Each panel shows the mean ± SEM of the normalized speed profiles of movement segments corresponding to a single neural state. Colors indicate different neural states. Data from RJ, see Supplementary Figure 3 for RS.

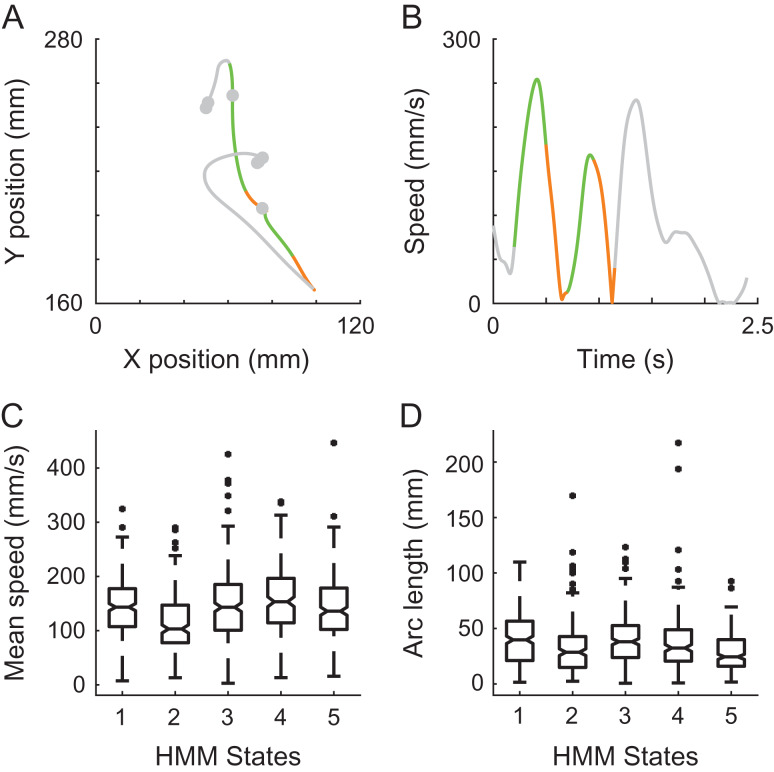
Notably, the neural states did not show a consistent selectivity to the magnitude of movement speed or movement amplitude. Figure 4A and B shows an example RTP trial, in which two strokes of movement were coupled with similar neural states, although they were executed with considerably different mean speeds and amplitudes. This non-selectivity was observed across trials, as can be seen in Figure 4C and D showing the distributions of speeds and amplitudes of the movement segments associated with each state. A non-selectivity of the neural states for position was also evident, yet as the workspace was relatively small this property was not further examined.

Figure 4.

Invariance of neural states to movement speed and amplitude. Position (A) and speed profile (B) of a single RTP trial, with two highlighted strokes that were executed with different amplitudes and mean speed, yet associated with similar neural states. Green and orange colors represent the decoded neural states. Gray represents the rest of the trial. (C) Boxplots of mean speed of all of the segments corresponding to each of the neural states show similar ranges and non-selectivity across states. (D) Boxplots of Euclidean length, similar to C. Data from RJ.

Center-out Reaching Movements Present a Similar Decomposition

A similar decomposition of the kinematic output was found in the center-out reaching movements. Mean segment duration was similar to that obtained in the RTP task, yet slightly shorter (200 ± 110 ms SD). Transitions between neural states occurred in proximity to speed extrema, and the neural states were associated with either accelerating or decelerating segments coupled with directional selectivity (one-way ANOVA for movement direction F(6 303) = 27, P < 0.001; one-way ANOVA for mean tangential acceleration across states F(6 303) = 85, P < 0.001; sign-test for mean tangential acceleration showed P < 0.001 for all states; Figure 5A–C). The majority of the bell-shaped speed profiles within the single reaches (bounded by the point at which the speed first exceed 15% of maximal speed and the first speed minimum point following peak speed) were segmented into two epochs (Fig. 5D). The mean absolute distance between peak speed and the nearest neural transition was 0.06 s, and the distribution of signed distances distributed approximately normal and was centered on zero (Fig. 5E). These results confirm the findings observed in the RTP task and demonstrate generalizability of the results across the tasks. Taken together, these findings indicate that transitions in the population activity repeatedly distinguish between epochs of acceleration and deceleration with a dependence on movement direction, within both sequential target pursuit movements and single center-out reaching movements.

Figure 5.

Directional and acceleration selectivity of neural states in the center-out task. (A) Examples of two center-out trials, with position (left) and speed profile (right) colored according to the identified neural states. Black dot represents the starting position. (B) Position data of all decoded trials, colored according to the identified neural states. (C) Each panel shows the mean ± SEM of the normalized speed profiles of movement segments corresponding to a single neural state. Radial histograms show the distribution of directions within each state. (D) Histogram of the number of neural segments found within single reaching movements, between the point at which the speed first exceeded 15% of maximal speed and the first speed minimum point following peak speed. (E) Histogram of the distances between peak speed and the nearest neural transition across trials.

Instantaneous Tuning for Kinematic Features Does not Explain the Observed Segmentation

As the observed segmentation is not directly predicted by previously proposed models of instantaneous directionally tuned neurons (Georgopoulos et al. 1982; Schwartz and Moran 2000), we tested whether it could emerge indirectly from such a model. To accomplish this, we used the center-out dataset and simulated a population of neurons coding for instantaneous direction or velocity. Specifically, we fitted a cosine function to each neuron’s firing rate to determine their preferred directions, simulated Poisson spike trains according to the obtained cosine functions and the instantaneous kinematics, and modeled the simulated spike trains using an HMM. As expected, performing the HMM analyses on the simulated population of neurons tuned to movement direction/velocity did not result in segmentation of the kinematic output into epochs of acceleration/deceleration. Performing a similar analysis using models that incorporated tuning for movement acceleration or a combination of velocity and acceleration showed a closer segmentation to the actual data, yet still did not capture the consistent segmentation we observed (Supplementary Fig. 4A). The average absolute distance between peak speed and the nearest neural transition was smaller in the actual data compared with the distances derived from the simulated populations, and the distribution of signed distances across trials was narrower (Supplementary Fig. 4B). These findings suggest that the neural state transitions were consistently closer to peak speed in the actual data than in the simulated populations. These observations were made across training and decoding of each simulated population using a range of 4–10 hidden states, with 5 iterations of model training per number of hidden states, implying that the tuning models we used were not sufficient to explain the decomposition we observed.

Modulation in the Activity of Single Cells Between Identified Epochs

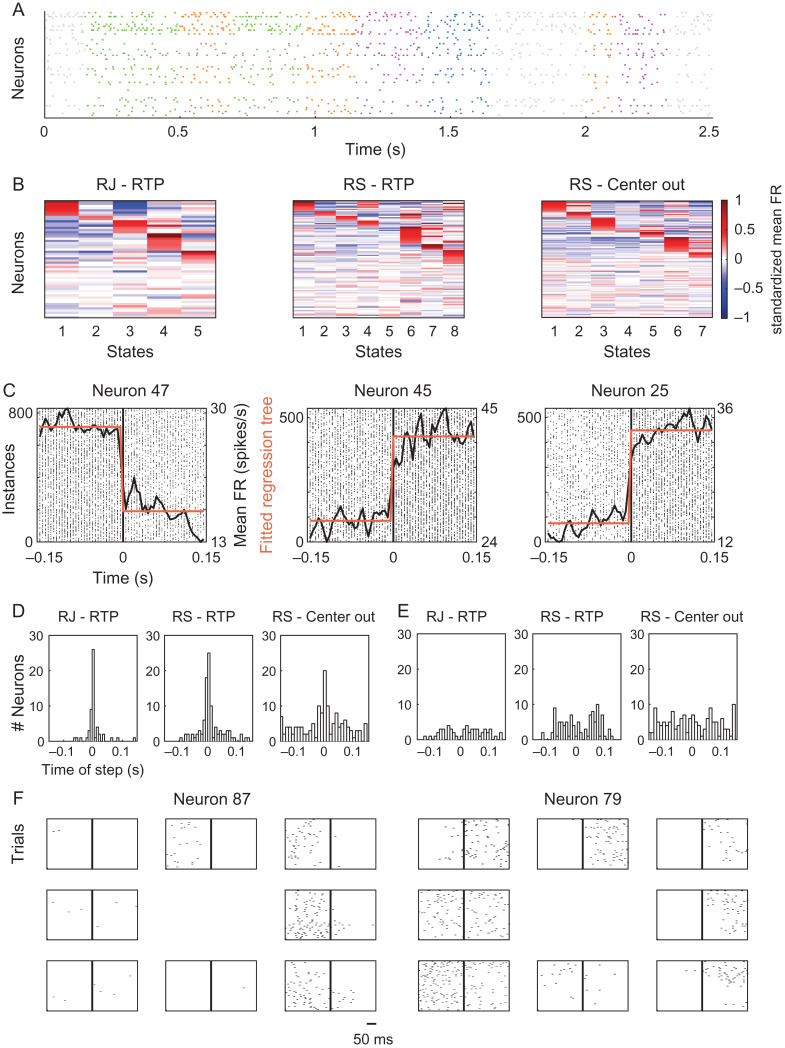
We then turned to characterize the neural activity underlying the obtained segmentation. Figure 6A presents example spike trains of the recorded cells during a single RTP trial, colored according to the decoded states. The mean firing rate of each unit was computed during each state, and standardized to indicate whether the cell fired above or below its mean in standard deviation units (Fig. 6B). Most units were active in multiple states, suggesting that each state was not represented by a completely separate ensemble of neurons.

Figure 6.

Modulation in the activity of single cells across neural states. (A) Example spike trains of single neurons during a single RTP trial, colored according to the decoded neural states. Data from RJ. (B) Standardized mean firing rates of single cells within each state. Red colors denote positive values, indicating neurons that were active above their mean, blue colors denote negative values, indicating neurons that were active below their mean. To aid in visualizing the active neurons in each state we sorted the cells (i.e., the rows of each matrix) by their activity in a sequential manner. We first placed cells that showed standardized values above 0.25 in the first state, then, from the remaining cells, cells that crossed the same threshold in the second state, and so on until the last state (red “block” within each state). Cells that did not cross this threshold in any of the states were placed last with no particular order. (C) Spike trains of 3 single cells aligned to the time point of transition between a specific pair of neural states (time zero, black vertical line), showing an abrupt change in firing rate. Plotted on top are the mean firing rate across the different instances (black line) and the fitted regression tree (step-like function in orange). Data from RJ. (D) Histograms of the time of the step of the best fitted regression tree for each neuron, for all 3 datasets, showing a peak around time zero – corresponding to the time of a state transition. (E) Similar to D, but here the regression trees were fitted to the mean firing rate calculated on firing patterns that were aligned to the middle point of the state, showing no evident peak at any time point. See also Supplementary Figure 5. (F) Spike trains of two example neurons recorded during the center-out trials, aligned to peak speed minus 100 ms lag (vertical line in the middle of each panel). The panels are organized according to the direction of motion of each condition. The neuron displayed on the left showed an increase in activity only during the acceleration phase, coupled with directional selectivity. The neuron displayed on the right showed an increase in activity during acceleration and deceleration, depending on the direction of movement.

Next, we inspected the activity of single units at a higher temporal resolution around time points of transition between states and examined the percentage of cells which showed a consistent modulation in the activity near these time points. This was accomplished by extracting spike trains of individual cells around transitions between specific state-pairs and averaging across instances associated with the same state-pair. Figure 6C shows single neurons that displayed a clear abrupt change in their firing rate at the time of transition between a specific pair of states. These single examples were not unique and a similar pattern of activity was found in multiple cells in all 3 datasets. We further fitted a regression tree to each such mean firing pattern constrained to a single partition, resulting in a step-like function. For each neuron, we took the state-pair transition which showed the highest goodness of fit with the fitted regression tree and extracted the time point of the corresponding step (goodness of fit was assessed according to the correlation values between the fitted regression tree and the mean firing rate, correlation values across neurons within each dataset were: RJ RTP task – mean R² = 0.78 ± 0.15 SD; RS RTP task – mean R² = 0.82 ± 0.09 SD; RS center-out task – mean R² = 0.57 ± 0.17 SD). Figure 6D shows histograms of the extracted step-times across the different neurons. In all datasets there was an evident peak in the histogram at time zero – corresponding to the time of transition between states. Specifically, 66%, 50% and 25% of the cells from RJ in the RTP task, RS in the RTP task, and RS in the center-out task, respectively, were fitted with a step function in which the step occurred less than 10 ms around the point of transition. This does not mean to imply that all of these units specifically exhibited a step-like change in activity, but that a consistent modulation in activity was coupled with the transition between states across many cells within each dataset. As a control, we did the same analysis on firing patterns aligned to the middle point of each state. The R² values obtained per neuron when aligning the firing patterns to the state transition points were statistically higher than the R² values obtained in the control analyses (P < 0.001 for each of the datasets, t-tests for dependent samples). Furthermore, the control analyses did not yield any evident peak, as apparent in the histograms presented in Figure 6E. Similarly, using randomly generated state transitions resulted in a poor fit of the regression trees and no evident peaks in the corresponding histograms (Supplementary Fig. 5). These results demonstrate that the segmentation obtained by the model resulted from a consistent modulation in the firing patterns across many cells, and imply that further segmentation, e.g., at the middle point of states, may not be as evident in the neural activity.

Finally, we tested whether there was a significant difference in the firing rates of single cells between behavioral epochs of acceleration and deceleration, regardless of the obtained neural segmentation. This was accomplished by comparing between the number of spikes that occurred during the acceleration phase and during the deceleration phase of the center-out reaching movements, per neuron. We found that 47% of the neurons showed a statistically significant difference between the sum of spikes during these epochs (pooling together all trials, t-test for paired samples, P < 0.05). Most of the neurons that exhibited a modulation in activity showed an increase in activity during either the acceleration phase or the deceleration phase (see Fig. 6F left). However, a subset of the neurons showed an increase in activity during acceleration when the reach was directed in a certain direction, and an increase in activity during deceleration when the reach was directed in the opposite direction (see Fig. 6F right). The latter type of neurons may not result in a statistically significant difference between the two epochs when pooling together all trials, suggesting that the actual percentage of neurons showing a significant modulation may be even greater than assessed. Interestingly, the increase in activity during one of the epochs seemed to be coupled in certain cases with a strong silencing effect during the other epoch, highlighting the difference between the two phases. Overall, these findings demonstrate the differential involvement of single cells during distinct phases of acceleration and deceleration, and suggest that the obtained segmentation was associated with a modulation in the activity of many cells within each dataset.

Population Activity Captures Different Subspaces and Follows Consistent Temporal Trajectories

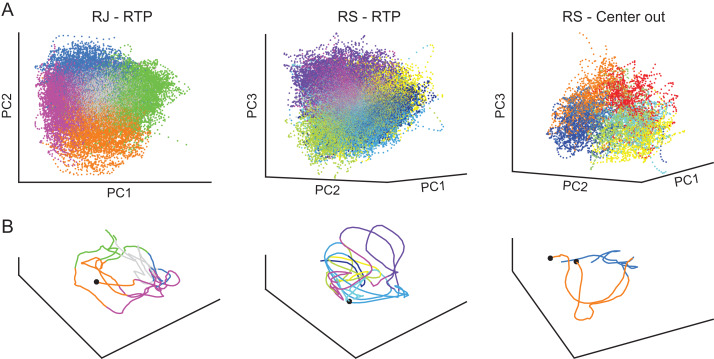
To examine the population activity that characterized the obtained neural states we performed a principal component analysis (PCA) on the firing patterns and visualized the population activity in a reduced space (Cunningham and Yu 2014). As expected, we found that the neural patterns associated with each of the states clustered in different regions of the low-dimensional space (Fig. 7A), demonstrating that each of the neural states was associated with a distinct subspace of the neural activity. Following evidence for specific population dynamics associated with different behavioral epochs (Afshar et al. 2011; Petreska et al. 2011; Churchland et al. 2012), we also traced the time-dependent neural trajectories of single trials (Fig. 7B). This revealed that different instances of a single neural state followed a similar neural trajectory, implying that the population activity within a single state was not only constrained to a specific subspace, but followed a certain time-dependent propagation. Indeed, the pair-wise distances between neural trajectories associated with the same state, calculated in the high-dimensional space, were smaller than the distances obtained using a temporal shuffle (see Methods) (RJ P < 0.05 for all states; RS RTP task P < 0.05 for all states, RS center-out task P < 0.05 for 5 out of 7 states, randomization tests). Although a more elaborate characterization of the population activity remains to be explored in future studies (e.g., using state-dependent continuous dynamics; Petreska et al. 2011), these results indicate that the discrete states identified by the HMM may be further characterized by specific dynamical regimes.

Figure 7.

Neural population activity across neural states. (A) Neural activation of all trials projected onto a reduced space using PCA, show clusters of activations corresponding to the decoded neural states. (B) Neural trajectories of single RTP trials (from RJ and RS, left and middle panels respectively), or of two center-out trials (RS, right panel), show that segments associated with the same neural state propagate in a similar path. Colors denote different neural states. Black dots represent the beginning of a trial. Axes were rotated to capture best viewing angle of the 3D space.

Discussion

Understanding movement compositionality and the underlying neural processes has been a long-standing challenge. Here, we examined the temporal structure of movement decomposition using an unsupervised analysis of the associated neural population activity, recorded from the primary motor cortex (M1) of macaque monkeys while performing a random target pursuit task (RTP) or a center-out task. Specifically, we used a hidden Markov model to segment the neural activity into sequences of neural states and examined how the neural segmentation was related to the behavioral output. Our results show that the obtained neural segmentation was strongly associated with a decomposition of the movement into distinct phases of acceleration and deceleration combined with directional selectivity, evident at the level of single trials in both sequential target pursuit movements and center-out reaching movements.

Emerging Neural Segmentation Reveals a Distinct Decomposition of Movement

Transitions between neural segments systematically coincided with minima and maxima points of the tangential velocity of the end-effector, partitioning the movement into accelerating and decelerating phases. Indeed, we were able to predict points of speed extrema based on neural state transitions across trials in both monkeys. Furthermore, each neural state was associated with either accelerating or decelerating movement segments executed towards a certain direction within the workspace (see Figs 2, 3, 5). Interestingly, the obtained neural states did not show selectivity to movement speed and amplitude (see Fig. 4), pointing to similarities in the neural activity preceding movements executed with varying speeds and amplitudes (Messier and Kalaska 1997; d’Avella et al. 2008; Kadmon Harpaz et al. 2014).

Parsing of movements at minima of the tangential velocity (often associated with curvature maxima (Abend et al. 1982; Flash and Hogan 1985)) has been proposed by multiple studies that have put forth the concatenation or superposition of bell-shaped speed profiles as a model for movement decomposition (Flash and Henis 1991; Milner 1992; Doeringer and Hogan 1998; Krebs et al. 1999). Segmentation at maxima of the tangential velocity has been less frequent, yet suggested to occur at inflection points (Viviani 1986), at time points of minimal angular velocity (Schwartz and Moran 1999), or at points of concatenation between parabolic segments (Polyakov et al. 2009). Our findings, however, demonstrate a consistent decomposition of the bell-shaped speed profiles at both minima and maxima of the tangential velocity, segmenting even simple straight reaching movements into two epochs.

A decomposition of the bell-shaped speed profile into two discrete epochs has been previously associated with muscle activations in single joint point-to-point movements, during which the acceleration phase is generated by an initial agonist burst, while breaking of the movement is related to the following antagonist burst, hypothesized to be independently controlled (Hoffman and Strick 1990). This implies that the segmentation we observed may represent the temporal recruitment of muscle synergies by M1, possibly organized downstream of M1 (Flament and Hore 1988; Wessberg and Vallbo 1995; Sergio and Kalaska 1998; Kargo and Giszter 2000, 2008, d’Avella et al. 2003, 2008, Cheung et al. 2005, 2009; Sergio et al. 2005; Yanai et al. 2008; Overduin et al. 2015). Indeed, previous studies have shown that the temporal organization of coordinated muscle activity occurs upstream of the spinal cord in discrete time-steps (Cordo et al. 1993; Saltiel and Rossignol 2004a, 2004b). However, the relation between the temporal recruitment of muscle groups and the kinematic output in multi-joint movements is not fully understood (Flanders et al. 1996). Thus, a single neural state may not be simply associated with the activation of a group of muscles, but may be coupled to the temporal context within the movement, e.g., initiating the movement versus breaking it (Jin et al. 2014), or involvement during flexion versus extension (Griffin et al. 2015). Although an examination of the muscle activation patterns is required for a more elaborate understanding of the relation between the obtained segmentation and muscle activity, our findings point to an intermediate level in the compositionality of movements and may reflect a mapping from kinematic elements to the required dynamic output (Yanai et al. 2008).

Epoch-based and Population-dependent Encoding

Our results present a strong modulation in the neural activity of the primary motor cortex between distinct epochs of acceleration and deceleration. Single cells showed a significant change in the firing rate between these epochs, with abrupt changes at the time of transitions between neural states (see Fig. 6). These results are not consistent with models suggesting a continuous encoding of instantaneous direction or velocity of the end-effector, which predict that a neuron tuned to the output direction will be active throughout the entire reach (Georgopoulos et al. 1982; Moran and Schwartz 1999), as was also evident in the simulations we performed. Simulations using models of instantaneous encoding that combined tuning for both velocity and acceleration better captured the segmentation we observed, yet still did not replicate the consistent modulations found in the actual data (see Supplementary Fig. 4). Although a different model of instantaneous encoding for velocity and acceleration may lead to a better description of the data (e.g., a non-linear relation between the two variables or sharper tuning curves), previous studies have demonstrated that expanded models incorporating instantaneous tuning for multiple kinematic features were not sufficient to explain firing patterns of cells in M1 (Paninski, Shoham, et al. 2004; Wu and Hatsopoulos 2006; Hatsopoulos et al. 2007; Churchland et al. 2012). In a recent study, Suway et al. (2017) examined center-out reaching movements and modeled the firing of neurons in M1 using a time-dependent directional tuning function. The authors found discrete epochs within the reaching movements, which were approximately timed with the epochs found in our study. An epoch-based encoding is supported by evidence demonstrating a dependence of the firing rates on kinematic parameters with multiple time delays (Paninski, Shoham, et al. 2004; Hatsopoulos et al. 2007), as well as by studies showing that pair-wise correlations between the neurons change abruptly between different behavioral epochs (Abeles et al. 1995; Vaadia et al. 1995; Elsayed et al. 2016). Our results support and extend these findings by identifying neural states that are associated with distinct phases of the kinematic output, and by demonstrating the modulation of single cells at the transition between these movement phases.

Although the firing rates of single units demonstrated a clear modulation in the transition between epochs, single cells were active in multiple neural states, suggesting that the population activity is required to distinguish between different behavioral phases. This is in agreement with previous studies which have shown that single units may be active in multiple behavioral epochs, such as during preparation and execution, but the overall population activity demonstrates distinct properties that differentiate between the epochs (Abeles et al. 1995; Elsayed et al. 2016). Visualizing the population activity in a low-dimensional space verified the difference between the states by revealing a clustered organization of the neural patterns corresponding to each of the states in distinct subspaces (see Fig. 7A). Furthermore, a neural state seemed to be characterized by a specific temporal sequence of activations – a unique neural trajectory, rather than a single point or random cloud of points in the corresponding subspace (see Fig. 7B). Recent work has demonstrated that the population activity during reaching movements follows a specific neural trajectory, namely characterized by rotational dynamics (Afshar et al. 2011; Churchland et al. 2012; Shenoy et al. 2013). As rotational dynamics can originate from phase-locked and phase-shifted oscillations, the breakdown of a single reaching movement may represent neural ensembles activated with shifted phases that facilitate the different kinematic epochs we observed (Bruno et al. 2015). However, further work is needed in order to fully characterize the population activity within the identified states. Still, the findings presented here, along with previous findings, imply that neural ensembles in the primary motor cortex represent movement in a more epoch-based and population-dependent encoding than previously hypothesized.

Conclusions

Studying movement segmentation by modeling the neuronal activity with an HMM, enabled an unsupervised detection of movement epochs at the CNS level, without imposing assumptions regarding the encoded movement features, the nature of the segmentation, or the duration of the composing elements. Analyzing datasets consisting of hundreds of trials, each different from the others, with a large range of movement parameters, we were able to find a repeatable structure in the population activity of neurons in M1. This structure accurately predicted distinct temporally extended segments of the behavioral output, which coincided with acceleration and deceleration segments, evident at the level of single trials. These findings provide new insight regarding the structure of movement composition and emphasize the differential involvement of the population activity in multiple epochs of the movement, pointing to an encoding scheme that involves the control of discrete phases of acceleration/deceleration at the level of M1. A mechanism in which the neural activity transitions between discrete states may underlie an intermittent control regime, which is often hypothesized in the context of movement decomposition (Craik 1947; Miall et al. 1986; Gawthrop et al. 2011; Karniel 2013). The intermittent commands that control the transitions between the states may arrive either from other brain regions (Matsumoto et al. 1999; Jin et al. 2014) or from internal oscillations (Hall et al. 2014). It will be important, however, to test the segmentation of the neural activity in movements that go beyond single point-to-point reaching and sequential target pursuit movements in order to generalize the conclusions of this work to other types of movements. Another important follow-up would be to trace the generation of the identified states during learning. Will any change occur in the identified states during the appearance of chunked or co-articulated movements? One hypothesis is that new states will emerge. Another hypothesis is that the transitions between existing states will be strengthened and occur more rapidly. The methods presented here can be used to examine such questions and possibly dissociate between these different hypotheses. A similar approach can be used to probe the segmentation of movement at different brain regions, possibly controlling different temporal scales, and to reveal the structure of movement composition at different levels of the motor hierarchy.

Funding

This work was supported by the National Institute of Neurological Disorders and Stroke at the National Institutes of Health (Grant R01 NS045853 to N.G.H.); The Israeli Center of Research Excellence (I-CORE) in the cognitive sciences (Grant 51/11h to T.F.), The VERE project funded under the European Seventh Framework Program (EC-ICT-257695 to T.F.); The United States – Israel Binational Science Foundation (Travel grant award to N.K.); and The CRCNS from the United States – Israel Binational Science Foundation and the United States National Science Foundation (Grant 2016740 to T.F.); T.F. is an incumbent of the Dr Hymie Moross Professorial Chair.