Figure 1.

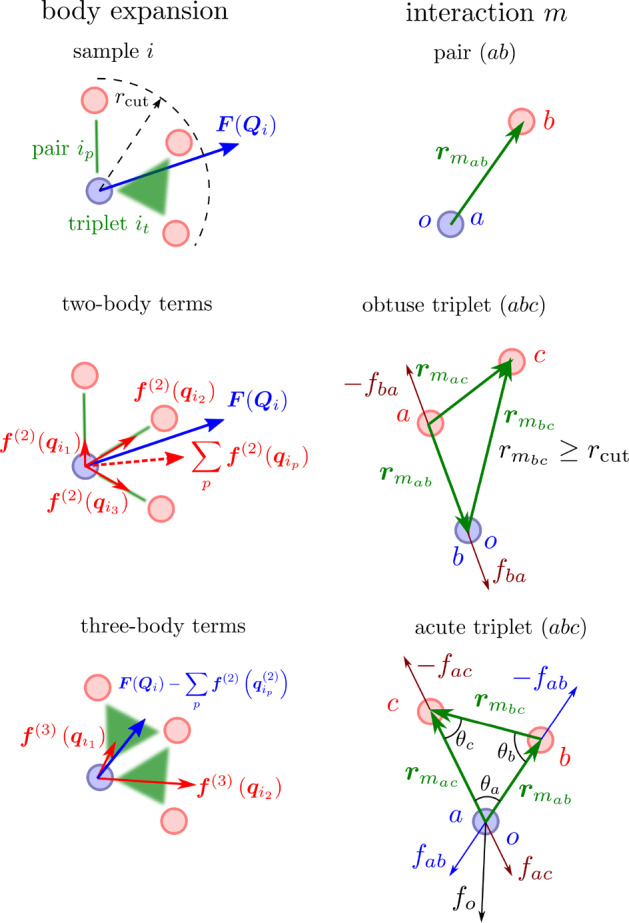
(left) Illustration of the body expansion of a configuration i on pairs and triplets, where the reference force F(Q_i) acts on the central particle. The two-body terms are shown by interparticle vectors (green lines) and result in total pairwise force ∑_p f⁽²⁾(q_ip⁽²⁾). A similar decomposition for triplets is used to fit the residual, i.e., total minus two-body, force. (right) Representations used for pairs and triplets. a, b, and c are the particles of the pair or triplet, and o is the central particle of the sample, which can be either a, b, or c. For triplets, two situations are possible: For obtuse triplets, with one edge larger than cutoff, the force on the central particle o = b is due to the reaction force on particle a. For acute triplets with all edges below the cutoff, the force on the central particle o = a, f_o, is a sum of two forces, f_ac and f_ab, which depend on all three angles, θ_a, θ_b, and θ_c. For vector differences, we use the standard convention, r_mab = r_mb – r_ma.