Summary
In early detection of disease, a single biomarker often has inadequate classification performance, making it important to identify new biomarkers to combine with the existing marker for improved performance. A biologically natural method for combining biomarkers is to use logic rules, e.g., the OR/AND rules. In our motivating example of early detection of pancreatic cancer, the established biomarker CA19-9 is only present in a subclass of cancers; it is of interest to identify new biomarkers present in the other subclasses and declare disease when either marker is positive. While there has been research on developing biomarker combinations using the OR/AND rules, inference regarding the incremental value of the new marker within this framework is lacking and challenging due to statistical non-regularity. In this article, we aim to answer the inferential question of whether combining the new biomarker achieves better classification performance than using the existing biomarker alone, based on a nonparametrically estimated OR rule that maximizes the weighted average of sensitivity and specificity. We propose and compare various procedures for testing the incremental value of the new biomarker and constructing its confidence interval, using bootstrap, cross-validation, and a novel fuzzy p-value-based technique. We compare the performance of different methods via extensive simulation studies and apply them to the pancreatic cancer example.
Keywords: Bootstrap, Combining biomarkers, Cross-validation, Fuzzy p-value, Incremental value, OR/AND rules
1. Introduction
In early detection of disease, a single biomarker often has inadequate classification performance. Identifying new biomarkers to combine with established predictors (biomarkers) for improved performance is an important research goal. For classification of binary diseases, a common modeling approach for combining biomarkers is using a likelihood-based logistic regression model, from which a marker combination score can be derived to subsequently generate a binary test based on a cut-off value. The use of logistic regression models has been well-studied in early detection; it yields optimal marker combination when the underlying risk model is correctly specified (McIntosh and Pepe, 2002), but may otherwise have suboptimal classification performance. Another commonly used approach in the applied literature for combining markers in a binary test is the use of logic rules (Etzioni and others, 2003), e.g., the “OR/AND” rules (Feng, 2010), which consider combination rules to be the set of “or-and” combinations of threshold rules in each biomarker. To declare an individual as disease-positive, the OR rule requires that either one or the other marker passes its individual threshold, while the AND rule requires that both markers pass their thresholds. For example, in early detection of pancreatic cancer, Tang and others (2015) considered a two-marker panel that declares disease if either the established biomarker CA19-9 exceeds a threshold OR a new discovered glycan marker exceeds a threshold. In a prostate cancer screening study, Gann and others (2002) showed that the addition of the ratio of free to total PSA (prostate-specific antigen) within a specific total PSA range with the OR/AND rules could simultaneously improve both specificity and sensitivity relative to the conventional strategy based on total PSA alone.
Logic combination rules are desirable for combining biomarkers mostly because of their simplicity and interpretability. For example, the OR rule is often preferred due to its biological appeal in detecting cancer, which is typically heterogeneous and composed of different subclasses. If biomarkers from each subclass can be identified, an OR rule combining these biomarkers is expected to boost the overall sensitivity without sacrificing much specificity. On the other hand, the AND rule is considered to be useful when individual biomarkers for combination have very high sensitivity and low specificity. Our research in this article is motivated by the development of biomarker combinations to improve early detection of pancreatic cancer. The current best marker for early detection of pancreatic cancer is the CA19-9 test, which detects the sialyl-Lewis A (sLeA) glycan. sLeA levels are not elevated in 25% of pancreatic cancers due to factors such as genetic inability. It is of interest to discover glycans other than sLeA that are overproduced in some pancreatic cancers that are low in sLeA. It is hoped that these glycans, when combined with CA19-9 using the OR rule (i.e., declaring a case if levels of either CA19-9 or the new marker are elevated), can improve the classification performance over CA19-9 alone (Tang and others, 2015). In other words, an important question that needs to be addressed is whether the new biomarker has significant incremental value when combined with an established biomarker, compared with using the established biomarker alone. While several authors have conducted statistical research on biomarker combinations using the OR/AND rules, the focus in the past has been mainly on algorithm development for finding the best combination instead of on making inference about the new biomarker’s incremental value. For example, Baker (2000) proposed a nonparametric multivariate algorithm that extended the idea of receiver-operating characteristic (ROC) cutpoints to multivariate positivity regions in order to find the optimal ROC curve. Etzioni and others (2003) considered classifying prostate cancers using OR/AND rules that combined total PSA with the ratio of free/total PSA; LOGIC regression (Ruczinski and others, 2003) was performed to find the best logic rule that maximizes the cross-validated weighted sum of sensitivity and specificity. Statistical research to answer the inferential question about the incremental value of a new biomarker, however, is lacking. As we will show next, this is a challenging problem due to the non-regularity of the incremental value estimator under the null hypothesis (i.e., when the new biomarker has no incremental value over the established biomarker). In this article, we aim to fill this gap. We will propose and compare various strategies for making inference regarding a new biomarker’s incremental value over an established biomarker. We consider a simple OR rule in this article for combining the established marker with the new marker, motivated by the pancreatic cancer example. However, the technique can be generalized to the AND rule or OR/AND rule combinations.
This article is organized as follows: In Section 2, we present an estimator for an OR rule that maximizes the weighted average of sensitivity and specificity, based on which the incremental value of the new marker is estimated. We develop procedures for testing the significance of the incremental value and for constructing its confidence interval (CI) utilizing the bootstrap, cross-validation, and a novel fuzzy p-value technique. In Section 3, we conduct extensive simulation studies to compare the performance of different methods. The application of the developed methods to the pancreatic cancer example is illustrated in Section 4. We finally make concluding remarks in Section 5.
2. Methodology
Let  be a binary disease outcome, with value
be a binary disease outcome, with value 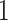 for diseased and
for diseased and  for non-diseased. Let
for non-diseased. Let  be an established biomarker (predictor) for predicting
be an established biomarker (predictor) for predicting  and let
and let  be a new biomarker that we are interested in evaluating. The objective is to test whether combination of
be a new biomarker that we are interested in evaluating. The objective is to test whether combination of 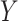 with
with 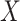 based on the OR rule offers any incremental value in classification performance over
based on the OR rule offers any incremental value in classification performance over  alone and to estimate the incremental value. Without loss of generality, we assume larger marker values are associated with higher risk of disease. Suppose a case is declared if either
alone and to estimate the incremental value. Without loss of generality, we assume larger marker values are associated with higher risk of disease. Suppose a case is declared if either  or
or  is elevated, i.e.,
is elevated, i.e.,  or
or 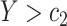 , for some thresholds
, for some thresholds 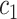 and
and 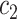 . We define sensitivity as
. We define sensitivity as 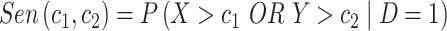 and specificity as
and specificity as  . For a test based on the biomarker
. For a test based on the biomarker  alone, sensitivity and specificity are defined as
alone, sensitivity and specificity are defined as  and
and  , respectively, for some threshold
, respectively, for some threshold 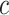 . To characterize the incremental performance of the new biomarker
. To characterize the incremental performance of the new biomarker  , we consider the weighted average of sensitivity and specificity as an overall summary measure of a model’s performance (Han and others, 2011), for pre-specified weight
, we consider the weighted average of sensitivity and specificity as an overall summary measure of a model’s performance (Han and others, 2011), for pre-specified weight  , for either the model based on
, for either the model based on  alone or the model based on the combination of
alone or the model based on the combination of  and
and  . The most common special case of the weighted average of sensitivity and specificity is the Youden’s index (Youden, 1950), which weights a model’s sensitivity and specificity equally. The equal weighting of sensitivity and specificity is oftentimes adopted in early stages of biomarker development when the objective is to discover a biomarker with good potential for future application based on a convenient case/control sample. This index will be adopted in our numerical studies in this article. In late phases of biomarker development, depending on the clinical practice where the biomarker will be utilized, weights for sensitivity/specificity can be chosen to reflect the relative importance of not missing the detection of a case versus not making false positive detection of a control, through a cost-benefit analysis. We define the incremental value of the new marker
. The most common special case of the weighted average of sensitivity and specificity is the Youden’s index (Youden, 1950), which weights a model’s sensitivity and specificity equally. The equal weighting of sensitivity and specificity is oftentimes adopted in early stages of biomarker development when the objective is to discover a biomarker with good potential for future application based on a convenient case/control sample. This index will be adopted in our numerical studies in this article. In late phases of biomarker development, depending on the clinical practice where the biomarker will be utilized, weights for sensitivity/specificity can be chosen to reflect the relative importance of not missing the detection of a case versus not making false positive detection of a control, through a cost-benefit analysis. We define the incremental value of the new marker  as the increase in the maximum value of the weighted average of sensitivity and specificity using the OR rule combining
as the increase in the maximum value of the weighted average of sensitivity and specificity using the OR rule combining  and
and  compared with the rule using
compared with the rule using  alone, i.e.,
alone, i.e.,
 |
(2.1) |
with some weight  . For the rule based on
. For the rule based on  alone, the rule that maximizes the summary measure of performance, i.e., the weighted average of sensitivity and specificity, is searched in a one-dimensional biomarker space. When using the OR rule combining
alone, the rule that maximizes the summary measure of performance, i.e., the weighted average of sensitivity and specificity, is searched in a one-dimensional biomarker space. When using the OR rule combining  with
with 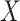 , the search is expanded to a two-dimensional biomarker space for the maximum performance measure. Since the optimization is performed over a larger space, the maximum possible value of the performance measure obtained using the OR rule is always greater than or equal to that using the rule based on
, the search is expanded to a two-dimensional biomarker space for the maximum performance measure. Since the optimization is performed over a larger space, the maximum possible value of the performance measure obtained using the OR rule is always greater than or equal to that using the rule based on  alone. That is, the rule based on
alone. That is, the rule based on 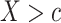 can be represented as a special case of the OR rule with
can be represented as a special case of the OR rule with  and
and  (or the largest value for a bounded
(or the largest value for a bounded  ). Thus the incremental value
). Thus the incremental value 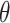 (2.1) is always non-negative.
(2.1) is always non-negative.
We note a connection between the maximizer of the weighted average of sensitivity and specificity and a logic regression risk model (Ruczinski and others, 2003). Specifically, suppose the risk of the disease conditional on the established biomarker  follows a logic regression model
follows a logic regression model
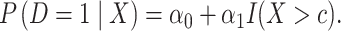 |
(2.2) |
When conditions in Result 1 below are satisfied, the threshold  in (2.2) will be the one that maximizes the weighted average of sensitivity and specificity in a binary classification rule based on
in (2.2) will be the one that maximizes the weighted average of sensitivity and specificity in a binary classification rule based on  alone. Similarly, suppose the risk of disease conditional on
alone. Similarly, suppose the risk of disease conditional on  and
and  follows a logic regression model
follows a logic regression model
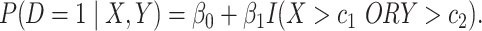 |
(2.3) |
When conditions in Result 2 below are satisfied, the thresholds 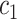 and
and  in (2.3) will be the corresponding thresholds for
in (2.3) will be the corresponding thresholds for  and
and  that maximize the weighted average of sensitivity and specificity in an OR rule.
that maximize the weighted average of sensitivity and specificity in an OR rule.
Result 1
For a binary rule based on
that classifies an observation as diseased if
, suppose the threshold value
is the maximizer of the weighted average of sensitivity and specificity, i.e.,
. If (2.2) holds, the CDF (cumulative distribution function) of
is not flat in a neighborhood of
,
and
, then
equals the parameter
indexing (2.2).
The proof of Result 1 is given in Appendix A of the supplementary material available at Biostatistics online. When the risk model (2.2) holds, the weighted average of sensitivity and specificity in the rule based on 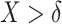 , i.e.,
, i.e., 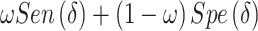 , can be represented as a linear function of the CDF of the biomarker
, can be represented as a linear function of the CDF of the biomarker  at
at 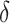 , for
, for 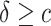 or
or 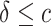 separately. The coefficient of the CDF of
separately. The coefficient of the CDF of  equals
equals 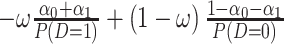 for
for 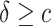 , and equals
, and equals 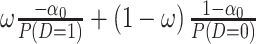 for
for  . As a result, the positivity condition of the coefficients stated in Result 1 guarantees that the weighted average of sensitivity and specificity reaches the maximum at
. As a result, the positivity condition of the coefficients stated in Result 1 guarantees that the weighted average of sensitivity and specificity reaches the maximum at  . Assuming larger marker value is associated with higher risk, i.e.,
. Assuming larger marker value is associated with higher risk, i.e.,  , then for a given risk model (2.2), the positivity condition is equivalent to
, then for a given risk model (2.2), the positivity condition is equivalent to
 |
An example for a given model (2.2) is presented in Figure 1 of the supplementary material available at Biostatistics online, which demonstrates how weighted sensitivity and specificity changes with 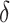 as
as 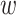 varies. Interestingly, the condition is always satisfied when
varies. Interestingly, the condition is always satisfied when  , i.e., equal weight is given to sensitivity and specificity.
, i.e., equal weight is given to sensitivity and specificity.
Fig. 1.
Distributions of  ,
,  , and
, and  based on 1000 simulated datasets, and distributions of
based on 1000 simulated datasets, and distributions of 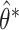 ,
, 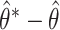 , and
, and 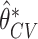 over 1000 bootstrap samples, for
over 1000 bootstrap samples, for  and
and  .
.
Result 2
For an OR rule based on
and
that classifies an observation as diseased if
or
, suppose the threshold value (
,
) for
and
is the maximizer of the weighted average of sensitivity and specificity, i.e.,
. If (2.3) holds, the CDF of
is not flat in the neighborhood of
,
and
, then
equals parameters
indexing (2.3).
The proof of Result 2 is given in Appendix B of the supplementary material available at Biostatistics online. Similarly as that in Result 1, we show that when the risk model (2.3) holds, the weighted average of sensitivity and specificity in an OR rule based on  and
and  can be written as a linear function of the joint CDF of biomarkers
can be written as a linear function of the joint CDF of biomarkers  and
and  at
at 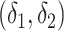 , for
, for  and
and 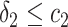 ,
,  and
and 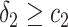 ,
, 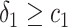 and
and 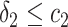 , or
, or  and
and 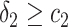 separately. The positivity condition of the coefficients in Result 2 ensures that the weighted average of sensitivity and specificity achieves its maximum at
separately. The positivity condition of the coefficients in Result 2 ensures that the weighted average of sensitivity and specificity achieves its maximum at 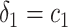 and
and  . Again assuming
. Again assuming  , for a given model (2.3), the positive condition results in
, for a given model (2.3), the positive condition results in
 |
which is always true for 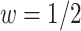 .
.
In general, even when the actual disease risk model conditional on biomarker(s) may not follow the conditions specified in Results 1 and 2, it is still appealing to identify classification rules based on  alone or an OR combination of
alone or an OR combination of  and
and  by maximizing the weighted average of sensitivity and specificity, given that the weighted average of sensitivity and specificity is a clinically meaningful operational criterion of practical interest. So is the estimation of the incremental value of
by maximizing the weighted average of sensitivity and specificity, given that the weighted average of sensitivity and specificity is a clinically meaningful operational criterion of practical interest. So is the estimation of the incremental value of  based on difference in model performance, as defined in equation (2.1).
based on difference in model performance, as defined in equation (2.1).
2.1. Inference
2.1.1. Estimation
To estimate the incremental value  , we consider nonparametric estimators of the classification rule based on either
, we consider nonparametric estimators of the classification rule based on either 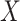 alone or combinations of
alone or combinations of  and
and  . In particular, we estimate threshold(s) in the corresponding rules by maximizing the weighted average of nonparametric estimates of sensitivity and specificity. Let subscripts
. In particular, we estimate threshold(s) in the corresponding rules by maximizing the weighted average of nonparametric estimates of sensitivity and specificity. Let subscripts  and
and  indicate case and control status, respectively, such that
indicate case and control status, respectively, such that  and
and  indicate biomarker measurements among cases and
indicate biomarker measurements among cases and  and
and 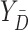 indicate biomarker measurements among controls. Let
indicate biomarker measurements among controls. Let  and
and 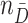 be sample sizes for cases and controls, respectively. We compute
be sample sizes for cases and controls, respectively. We compute 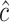 as the maximizer in
as the maximizer in 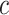 of
of 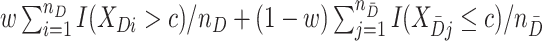 . Similarly, we compute
. Similarly, we compute  and
and  as the maximizers in
as the maximizers in  and
and  of
of  . In our simulation studies and real data example, we adopt the grid-search method to obtain the maximizers
. In our simulation studies and real data example, we adopt the grid-search method to obtain the maximizers 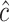 ,
,  , and
, and  . For the rule based on X alone, we take the grid points to include all unique values of
. For the rule based on X alone, we take the grid points to include all unique values of  from the sample; for the OR rule combining
from the sample; for the OR rule combining  with
with  , the search space is set to include all combinations of unique values of
, the search space is set to include all combinations of unique values of  and
and  from the sample. These grid searches are guaranteed to find the thresholds maximizing the empirical weighted average of sensitivity and specificity. Based on
from the sample. These grid searches are guaranteed to find the thresholds maximizing the empirical weighted average of sensitivity and specificity. Based on  ,
, 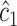 , and
, and  , we then estimate
, we then estimate 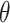 nonparametrically as
nonparametrically as
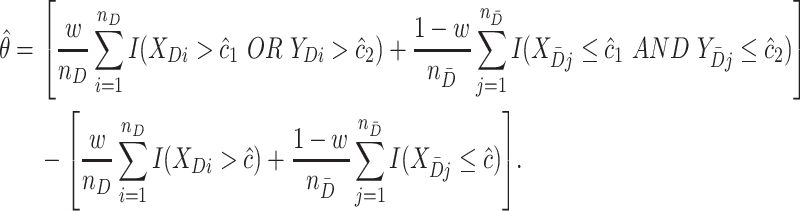 |
Note however this “naïve” estimator estimates the rule and its performance from the same dataset and thus is subject to overfitting bias. To reduce overfitting, a K-fold cross-validation method can be adopted instead. In performing cross-validation, first the dataset is split into  mutually exclusive and exhaustive subsets stratified on case/control status. Each time, one of the
mutually exclusive and exhaustive subsets stratified on case/control status. Each time, one of the  subsets is used as the test set and the remaining
subsets is used as the test set and the remaining  subsets are combined together to form a training set. The thresholds are estimated based on the training set and then they are used to obtain the incremental value estimator based on the
subsets are combined together to form a training set. The thresholds are estimated based on the training set and then they are used to obtain the incremental value estimator based on the  test set, denoted by
test set, denoted by  . The cross-validated estimator of incremental value is produced by taking average of the resulting
. The cross-validated estimator of incremental value is produced by taking average of the resulting  estimators, i.e.,
estimators, i.e.,
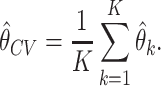 |
Next we investigate approaches to test the hypothesis that  has significant incremental value when combined with
has significant incremental value when combined with  through an OR rule, i.e., to test
through an OR rule, i.e., to test
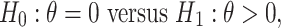 |
as well as approaches to construct the CI of the incremental value. We will propose a novel fuzzy p-value-based testing procedure and investigate various bootstrap-based approaches for inference.
2.1.2. Hypothesis testing
To perform the one-sided hypothesis test, we consider both a fuzzy p-value based approach and the bootstrap based approaches as described below.
A challenge with the test of incremental value in this problem setting is the non-regularity of the incremental value estimator under the null hypothesis. In other words, the naïve nonparametric estimator 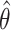 is not asymptotically normal, so the standard testing procedure based on asymptotic normality of the test statistics is not applicable here. Figure 1 presents numerical examples of distribution of
is not asymptotically normal, so the standard testing procedure based on asymptotic normality of the test statistics is not applicable here. Figure 1 presents numerical examples of distribution of 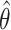 for various
for various 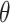 values. When the null hypothesis is true (
values. When the null hypothesis is true (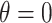 ),
), 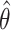 is heavily right-skewed with a peak at zero. The distribution of
is heavily right-skewed with a peak at zero. The distribution of  approaches normality as
approaches normality as 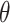 moves away from zero.
moves away from zero.
Fuzzy p-value Approach In this section, we propose a novel test for the incremental value of  that leverages the fact that
that leverages the fact that  will converge to zero under the null given some regularity conditions. Let
will converge to zero under the null given some regularity conditions. Let 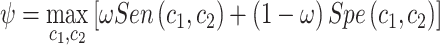 and
and  . Under some regularity conditions, the key of which is that the
. Under some regularity conditions, the key of which is that the 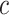 maximizing
maximizing 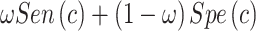 is unique, one can show that the nonparametric maximum likelihood estimator (NPMLE)
is unique, one can show that the nonparametric maximum likelihood estimator (NPMLE) 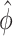 satisfies the following asymptotically linear expansion
satisfies the following asymptotically linear expansion
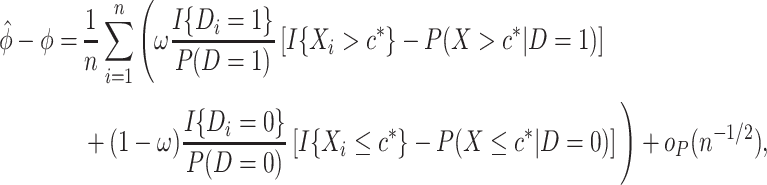 |
(2.4) |
where above 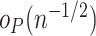 represents a term that converges to zero in probability once multiplied by
represents a term that converges to zero in probability once multiplied by  . A sketch of the argument for the above expansion is provided in Appendix C of the supplementary material available at Biostatistics online.
. A sketch of the argument for the above expansion is provided in Appendix C of the supplementary material available at Biostatistics online.
The term in the sum on the right-hand side of (2.4) represents the canonical gradient of the parameter  (Bickel and others, 1998). Under the independent and identically distributed (i.i.d.) assumption,
(Bickel and others, 1998). Under the independent and identically distributed (i.i.d.) assumption,  as the sample size goes to infinity, where
as the sample size goes to infinity, where 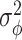 is the efficiency bound for regular and asymptotically linear estimators for
is the efficiency bound for regular and asymptotically linear estimators for  within the nonparametric model. Here, we have made the simplifying assumption that the data are a sample of
within the nonparametric model. Here, we have made the simplifying assumption that the data are a sample of  i.i.d. observations, so that standard efficiency theory can be applied. Nonetheless, if a fixed number of cases and controls are sampled, then the dominant term above breaks into the sum of an empirical mean over cases and an empirical mean over controls, and the remainder term will remain negligible. Hence, central limit theorem results can be obtained in that case as well. Under similar regularity conditions to those needed for (2.4), the key of which is that the
i.i.d. observations, so that standard efficiency theory can be applied. Nonetheless, if a fixed number of cases and controls are sampled, then the dominant term above breaks into the sum of an empirical mean over cases and an empirical mean over controls, and the remainder term will remain negligible. Hence, central limit theorem results can be obtained in that case as well. Under similar regularity conditions to those needed for (2.4), the key of which is that the  in the closure of the support of
in the closure of the support of 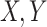 maximizing
maximizing  are unique,
are unique,
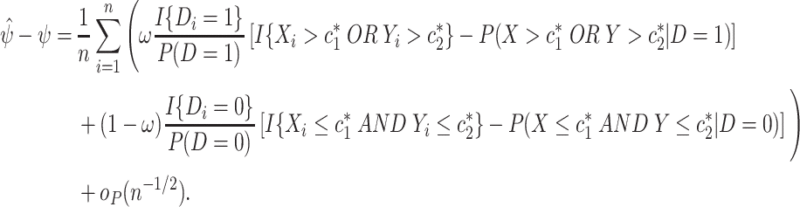 |
(2.5) |
Hence, 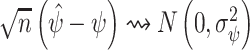 . Under the assumptions needed for (2.4) and (2.5) to hold, the null hypothesis that
. Under the assumptions needed for (2.4) and (2.5) to hold, the null hypothesis that  implies that
implies that 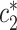 falls at the upper edge of the support for
falls at the upper edge of the support for 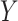 , in the sense that it is equal to the smallest number
, in the sense that it is equal to the smallest number 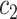 such that
such that  . In this case, the summation on the right-hand side above is equal to the summation on the right-hand side of (2.4), i.e. the right-hand sides of (2.4) and (2.5) are equivalent up to an
. In this case, the summation on the right-hand side above is equal to the summation on the right-hand side of (2.4), i.e. the right-hand sides of (2.4) and (2.5) are equivalent up to an  term. Because
term. Because  under the null, we see that
under the null, we see that
 |
Now, using that  and
and 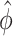 are consistent estimators, we also have that
are consistent estimators, we also have that
 |
i.e., for any fixed 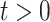 ,
,  as
as 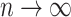 .
.
We now use these facts to introduce a fuzzy p-value. Let  denote a cumulative distribution function for a continuous random variable on
denote a cumulative distribution function for a continuous random variable on 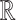 . By the above two facts, if
. By the above two facts, if 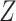 is a random variable with cumulative distribution function
is a random variable with cumulative distribution function  , under the null
, under the null 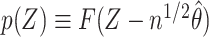 converges to a standard uniform random variable, whereas, under a fixed alternative,
converges to a standard uniform random variable, whereas, under a fixed alternative,  converges in probability to
converges in probability to 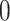 . Note that
. Note that  is a valid fuzzy p-value according to the definition given in Geyer and Meeden (2005). To generate a concrete decision, one could sample
is a valid fuzzy p-value according to the definition given in Geyer and Meeden (2005). To generate a concrete decision, one could sample 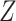 from
from  and reject if
and reject if 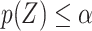 . Under the null hypothesis, the null will reject with probability approaching
. Under the null hypothesis, the null will reject with probability approaching 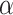 . In our simulation, we use
. In our simulation, we use  in computation of the fuzzy p-value to minimize over-fitting bias in small sample size; we let
in computation of the fuzzy p-value to minimize over-fitting bias in small sample size; we let 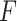 equal to the CDF of the normal distribution
equal to the CDF of the normal distribution  , where
, where 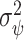 is estimated with
is estimated with 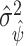 via the bootstrap. Alternatively, a Wald-type estimate of
via the bootstrap. Alternatively, a Wald-type estimate of 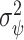 could be obtained by computing the empirical variance of the term in the sum in (2.5), where here unknown probabilities and maximizing thresholds would be replaced by estimates.
could be obtained by computing the empirical variance of the term in the sum in (2.5), where here unknown probabilities and maximizing thresholds would be replaced by estimates.
Bootstrap Approach A commonly used approach for performing hypothesis tests is to construct bootstrap (Efron and Tibshirani, 1994) CIs for an estimand and evaluate whether the CI covers the parameter value specified in the null hypothesis. Here, we investigate different bootstrap methods to perform the hypothesis test about the incremental value raised by  . We first consider bootstrap procedures based on the naive estimate of
. We first consider bootstrap procedures based on the naive estimate of  , because they are computationally simple and commonly used in practice. Both empirical and percentile bootstrap methods are considered. Suppose we have a data set of size
, because they are computationally simple and commonly used in practice. Both empirical and percentile bootstrap methods are considered. Suppose we have a data set of size  , from which we draw
, from which we draw  random samples of size
random samples of size  with replacement, stratified on case/control status. Let
with replacement, stratified on case/control status. Let 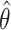 and
and  be the nonparametric incremental value estimates based on the original data set and the bootstrap samples, respectively. The one-sided
be the nonparametric incremental value estimates based on the original data set and the bootstrap samples, respectively. The one-sided 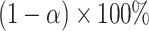 empirical bootstrap CIs are constructed as
empirical bootstrap CIs are constructed as  , where
, where 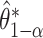 denotes the
denotes the  quantile of
quantile of 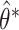 . The one-sided
. The one-sided 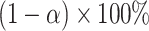 percentile bootstrap CIs are constructed as
percentile bootstrap CIs are constructed as 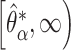 . The one-sided test for the incremental value being greater than zero can be based on whether the lower bound of the
. The one-sided test for the incremental value being greater than zero can be based on whether the lower bound of the 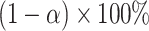 one-sided bootstrap CI is above zero. Percentile bootstrap CI has been widely used in biomarker research for characterizing and comparing biomarker performances. However, its validity requires symmetry in the distribution of the estimator (Van derVaart, 1998), which is clearly violated under the null hypothesis in our problem setting based on
one-sided bootstrap CI is above zero. Percentile bootstrap CI has been widely used in biomarker research for characterizing and comparing biomarker performances. However, its validity requires symmetry in the distribution of the estimator (Van derVaart, 1998), which is clearly violated under the null hypothesis in our problem setting based on  . In contrast, the rationale behind the empirical bootstrap is to approximate the distribution of
. In contrast, the rationale behind the empirical bootstrap is to approximate the distribution of  by the distribution of
by the distribution of  . From Figure 1, the right tails of the distributions for
. From Figure 1, the right tails of the distributions for 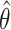 and
and  agree reasonably well, suggesting the potential of testing the incremental value based on the lower confidence limit of the one-sided empirical bootstrap CI based on
agree reasonably well, suggesting the potential of testing the incremental value based on the lower confidence limit of the one-sided empirical bootstrap CI based on 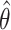 . Nonetheless, we emphasize that we do not currently have theory supporting the validity of the bootstrap under the null, and therefore our simulation will serve as preliminary evidence for or against its validity. Hereafter, we refer to the approaches based on empirical bootstrap CI or percentile bootstrap CI of
. Nonetheless, we emphasize that we do not currently have theory supporting the validity of the bootstrap under the null, and therefore our simulation will serve as preliminary evidence for or against its validity. Hereafter, we refer to the approaches based on empirical bootstrap CI or percentile bootstrap CI of 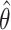 as EB and PB, respectively.
as EB and PB, respectively.
From Figure 1, the distribution of the cross-validated estimate 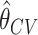 is close to normal under both the null and the alternative hypotheses, suggesting the potential of using the Wald-test for incremental value based on the cross-validated incremental estimate. Thus we also consider a one-sided Wald test for the incremental value. Let
is close to normal under both the null and the alternative hypotheses, suggesting the potential of using the Wald-test for incremental value based on the cross-validated incremental estimate. Thus we also consider a one-sided Wald test for the incremental value. Let 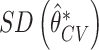 be the standard deviation of cross-validated incremental value estimate obtained using bootstrap resampling. The Wald test rejects the null if
be the standard deviation of cross-validated incremental value estimate obtained using bootstrap resampling. The Wald test rejects the null if 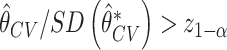 , where
, where 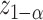 is the
is the  quantile of the standard normal distribution. We refer to this approach as Wald.CV. Note that one might also consider combining other bootstrap procedures, e.g., percentile or empirical bootstrap, with cross-validated estimate of
quantile of the standard normal distribution. We refer to this approach as Wald.CV. Note that one might also consider combining other bootstrap procedures, e.g., percentile or empirical bootstrap, with cross-validated estimate of  . Through numerical explorations, we found that when cross-validated estimates are used, performance of those alternative bootstrap procedures is either comparable or inferior to Wald.CV (results omitted). Thus we choose to focus on presenting Wald.CV results in the rest of the article.
. Through numerical explorations, we found that when cross-validated estimates are used, performance of those alternative bootstrap procedures is either comparable or inferior to Wald.CV (results omitted). Thus we choose to focus on presenting Wald.CV results in the rest of the article.
2.1.3. Estimation of two-sided CI
In practice, besides testing the incremental value of a new biomarker, it is also of interest to understand the uncertainty of the incremental value estimate. We consider the construction of a two-sided CI for increment value using the Wald.CV approach mentioned before. Specifically, the two-sided 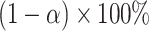 Wald CIs for
Wald CIs for  are constructed as
are constructed as 
 .
.
3. Simulation study
In this section, we conduct simulation studies to compare the performance of the methods described in Section 2 for testing and making inference about a new biomarker’s incremental value. Here, we consider equally weighted sensitivity and specificity as the classification performance measure and define 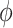 and
and 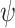 as the optimal average sensitivity and specificity based on an established marker alone or based on its combination with a new marker with an OR rule. The incremental value
as the optimal average sensitivity and specificity based on an established marker alone or based on its combination with a new marker with an OR rule. The incremental value 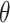 is then defined as the difference between
is then defined as the difference between 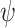 and
and  .
.
Let 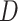 be a binary disease outcome. Let
be a binary disease outcome. Let  and
and  be two biomarkers that are independently distributed; each follows the standard normal distribution. We consider two types of scenarios where the underlying true risk model is (i) a logic model for the risk of
be two biomarkers that are independently distributed; each follows the standard normal distribution. We consider two types of scenarios where the underlying true risk model is (i) a logic model for the risk of 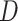 conditional on
conditional on  and
and  :
: 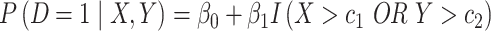 with thresholds
with thresholds 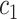 ,
,  and parameters
and parameters 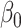 ,
, 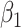 and (ii) a logistic risk model
and (ii) a logistic risk model 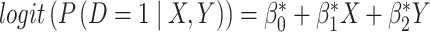 , yet investigators have adopted the simple OR rule to combine
, yet investigators have adopted the simple OR rule to combine  and
and  . In both scenarios, we set disease prevalence
. In both scenarios, we set disease prevalence 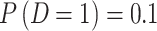 with appropriate selection of
with appropriate selection of 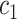 ,
, 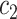 ,
, 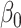 ,
, 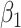 ,
, 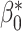 ,
,  , and
, and 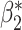 . For the logic model, the true incremental value of
. For the logic model, the true incremental value of  is
is  when
when  , otherwise it is greater than
, otherwise it is greater than 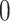 . We consider five different values of the threshold for biomarker
. We consider five different values of the threshold for biomarker  ,
,  ,
, 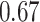 ,
, 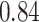 ,
, 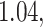 and
and 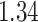 , which correspond to the
, which correspond to the 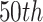 ,
, 
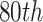 ,
, 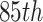 , and
, and  percentiles of the standard normal distribution, respectively. In the following, we select different values of
percentiles of the standard normal distribution, respectively. In the following, we select different values of  ,
,  or
or 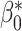 ,
,  ,
, 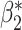 to achieve a wide variety of classification performance based on
to achieve a wide variety of classification performance based on  alone (
alone ( ) or based on the OR combination of
) or based on the OR combination of  and
and  (
(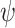 ). We consider scenarios with classification performance of the established biomarker
). We consider scenarios with classification performance of the established biomarker 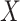 equal to 0.6, 0.7, 0.8, or 0.9. A range of incremental values
equal to 0.6, 0.7, 0.8, or 0.9. A range of incremental values  ,
,  , or
, or 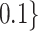 are considered in our simulation studies.
are considered in our simulation studies.
We consider case/control samples with equal numbers of cases and controls 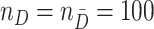 ,
,  or
or  randomly sampled from the population, based on which we compute the naïve performance estimate
randomly sampled from the population, based on which we compute the naïve performance estimate 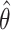 and the cross-validated estimate
and the cross-validated estimate 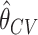 based on 10-fold cross-validation. For each setting, we evaluate bias of
based on 10-fold cross-validation. For each setting, we evaluate bias of  and
and 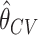 . We compare four different methods to perform the one-sided test at significance level
. We compare four different methods to perform the one-sided test at significance level 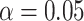 for incremental value with respect to Type I error rate and power: (i) EB: the method based on empirical bootstrap CI using
for incremental value with respect to Type I error rate and power: (i) EB: the method based on empirical bootstrap CI using  , (ii) PB: the method based on percentile bootstrap CI using
, (ii) PB: the method based on percentile bootstrap CI using  , (iii) Wald.CV, Wald test using
, (iii) Wald.CV, Wald test using  , and (iv) the fuzzy p-value approach. In addition, we examine coverage of the
, and (iv) the fuzzy p-value approach. In addition, we examine coverage of the  two-sided CI of incremental value using the Wald.CV method. In each setting, 1000 Monte-Carlo simulations are conducted with 1000 bootstrap replicates constructed stratified on case/control status. The simulation results for various scenarios and sampling size at each fixed
two-sided CI of incremental value using the Wald.CV method. In each setting, 1000 Monte-Carlo simulations are conducted with 1000 bootstrap replicates constructed stratified on case/control status. The simulation results for various scenarios and sampling size at each fixed  are summarized in Tables 1, 2, and 3. Corresponding results under the local alternative where
are summarized in Tables 1, 2, and 3. Corresponding results under the local alternative where 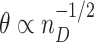 are presented in Table 1 in the supplementary material available at Biostatistics online.
are presented in Table 1 in the supplementary material available at Biostatistics online.
Table 1.
Naïve and cross-validated (CV) estimates of incremental value and corresponding standard deviation (SD) in the parenthesis based on 1000 Monte Carlo simulations under different underlying models and scenarios.  indicates the performance of biomarker
indicates the performance of biomarker  alone and
alone and  indicates the incremental value
indicates the incremental value
| Correctly specified model (logic model) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|

|

|

|

|
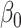
|

|
Estimate (SD) | CV Estimate (SD) | ||||

|

|
||||||||||
| 100 | 250 | 500 | 100 | 250 | 500 | ||||||
| 0 | 0.6 | 0 |
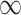
|
0.064 | 0.072 | 0.008 | 0.003 | 0.004 |
 0.012 0.012 |
 0.006 0.006 |
 0.005 0.005 |
| (0.010) | (0.004) | (0.004) | (0.025) | (0.010) | (0.011) | ||||||
| 0 | 0.6 | 0.84 |

|
0.078 | 0.113 | 0.012 | 0.005 | 0.003 |
 0.009 0.009 |
 0.005 0.005 |
 0.003 0.003 |
| (0.005) | (0.006) | (0.003) | (0.028) | (0.012) | (0.007) | ||||||
| 0 | 0.7 | 0 |
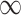
|
0.028 | 0.144 | 0.002 | 0.001 | 0.000 |
 0.008 0.008 |
 0.003 0.003 |
 0.002 0.002 |
| (0.004) | (0.001) | (0.001) | (0.010) | (0.003) | (0.002) | ||||||
| 0 | 0.7 | 0.84 |
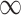
|
0.055 | 0.225 | 0.005 | 0.002 | 0.001 |
 0.010 0.010 |
 0.004 0.004 |
 0.002 0.002 |
| (0.007) | (0.003) | (0.001) | (0.014) | (0.006) | (0.003) | ||||||
| 0 | 0.8 | 0.67 |
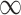
|
0.028 | 0.288 | 0.002 | 0.001 | 0.000 |
 0.007 0.007 |
 0.003 0.003 |
 0.001 0.001 |
| (0.003) | (0.001) | (0.001) | (0.007) | (0.003) | (0.001) | ||||||
| 0 | 0.8 | 0.84 |
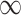
|
0.033 | 0.338 | 0.002 | 0.001 | 0.000 |
 0.007 0.007 |
 0.003 0.003 |
 0.001 0.001 |
| (0.004) | (0.002) | (0.001) | (0.008) | (0.003) | (0.002) | ||||||
| 0 | 0.9 | 1.04 |
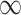
|
0.015 | 0.565 | 0.001 | 0.000 | 0.000 |
 0.006 0.006 |
 0.002 0.002 |
 0.001 0.001 |
| (0.002) | (0.001) | (0.000) | (0.005) | (0.002) | (0.001) | ||||||
| 0 | 0.9 | 1.34 |

|
0.021 | 0.879 | 0.001 | 0.000 | 0.000 |
 0.006 0.006 |
 0.003 0.003 |
 0.001 0.001 |
| (0.003) | (0.001) | (0.001) | (0.005) | (0.002) | (0.001) | ||||||
| 0.05 | 0.6 | 0.84 | 1.15 | 0.061 | 0.129 | 0.054 | 0.051 | 0.051 | 0.040 | 0.047 | 0.048 |
| (0.022) | (0.015) | (0.011) | (0.037) | (0.021) | (0.013) | ||||||
| 0.05 | 0.7 | 0.84 | 1.53 | 0.040 | 0.240 | 0.053 | 0.051 | 0.051 | 0.044 | 0.048 | 0.049 |
| (0.019) | (0.012) | (0.009) | (0.027) | (0.014) | (0.010) | ||||||
| 0.05 | 0.8 | 0.84 | 1.73 | 0.018 | 0.352 | 0.051 | 0.050 | 0.050 | 0.044 | 0.048 | 0.049 |
| (0.017) | (0.010) | (0.008) | (0.021) | (0.013) | (0.008) | ||||||
| 0.05 | 0.9 | 1.04 | 2.01 | 0.003 | 0.577 | 0.050 | 0.050 | 0.050 | 0.045 | 0.048 | 0.049 |
| (0.016) | (0.010) | (0.007) | (0.018) | (0.011) | (0.007) | ||||||
| 0.1 | 0.6 | 0.84 | 0.67 | 0.040 | 0.150 | 0.099 | 0.099 | 0.100 | 0.096 | 0.098 | 0.100 |
| (0.031) | (0.020) | (0.014) | (0.045) | (0.025) | (0.016) | ||||||
| 0.1 | 0.7 | 0.84 | 1.15 | 0.023 | 0.257 | 0.099 | 0.100 | 0.100 | 0.095 | 0.099 | 0.099 |
| (0.026) | (0.016) | (0.012) | (0.031) | (0.018) | (0.012) | ||||||
| 0.1 | 0.8 | 0.84 | 1.38 | 0.002 | 0.368 | 0.099 | 0.100 | 0.100 | 0.096 | 0.099 | 0.099 |
| (0.024) | (0.015) | (0.011) | (0.027) | (0.016) | (0.011) | ||||||
| Mis-specified model (logistic model) | |||||||||||

|

|

|

|
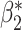
|
Estimate (SD) | CV estimate (SD) | |||||

|

|
||||||||||
| 100 | 250 | 100 | 250 | 100 | 250 | ||||||
| 0 | 0.6 |
 2.284 2.284 |
0.47 | 0 | 0.009 | 0.004 | 0.002 |
 0.010 0.010 |
 0.005 0.005 |
 0.003 0.003 |
|
| (0.011) | (0.005) | (0.003) | (0.028) | (0.013) | (0.007) | ||||||
| 0 | 0.7 |
 2.613 2.613 |
1.1 | 0 | 0.004 | 0.001 | 0.001 |
 0.008 0.008 |
 0.004 0.004 |
 0.002 0.002 |
|
| (0.006) | (0.002) | (0.001) | (0.016) | (0.006) | (0.003) | ||||||
| 0 | 0.8 |
 3.358 3.358 |
1.94 | 0 | 0.001 | 0.001 | 0.000 |
 0.007 0.007 |
 0.003 0.003 |
 0.001 0.001 |
|
| (0.003) | (0.001) | (0.001) | (0.009) | (0.004) | (0.002) | ||||||
| 0 | 0.9 |
 5.501 5.501 |
3.90 | 0 | 0.001 | 0.000 | 0.000 |
 0.006 0.006 |
 0.002 0.002 |
 0.001 0.001 |
|
| (0.002) | (0.001) | (0.000) | (0.005) | (0.002) | (0.001) | ||||||
| 0.1 | 0.6 |
 2.680 2.680 |
0.5 | 1.05 | 0.111 | 0.108 | 0.105 | 0.099 | 0.103 | 0.100 | |
| (0.036) | (0.025) | (0.018) | (0.057) | (0.037) | (0.025) | ||||||
| 0.1 | 0.7 |
 3.946 3.946 |
1.5 | 2.02 | 0.112 | 0.106 | 0.105 | 0.099 | 0.097 | 0.099 | |
| (0.035) | (0.023) | (0.016) | (0.053) | (0.033) | (0.022) | ||||||
| 0.1 | 0.8 |
 19.534 19.534 |
10.5 | 10.9 | 0.108 | 0.106 | 0.104 | 0.098 | 0.101 | 0.100 | |
| (0.028) | (0.019) | (0.014) | (0.042) | (0.026) | (0.018) |
Table 2.
Type I error rate and power of one-sided test from the empirical bootstrap (EB), percentile bootstrap (PB), Wald using cross-validation (Wald.CV), and fuzzy p-value methods, under different underlying models and scenarios.  indicates the performance of biomarker
indicates the performance of biomarker  alone and
alone and  indicates the incremental value
indicates the incremental value
| Correctly specified model (logic model) | |||||||
|---|---|---|---|---|---|---|---|
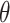
|

|
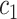
|

|
EB | PB | Wald.CV | Fuzzy p-value |
| Type I error rate | |||||||
| 0 | 0.6 | 0 | 100 | 0.015 | 0.132 | 0.006 | 0.056 |
| 250 | 0.007 | 0.135 | 0.003 | 0.034 | |||
| 500 | 0.023 | 0.344 | 0.008 | 0.055 | |||
| 0.84 | 100 | 0.033 | 0.229 | 0.011 | 0.073 | ||
| 250 | 0.015 | 0.256 | 0.002 | 0.042 | |||
| 500 | 0.018 | 0.277 | 0.004 | 0.036 | |||
| 0.7 | 0 | 100 | 0.001 | 0.009 | 0.001 | 0.038 | |
| 250 | 0.005 | 0.006 | 0.001 | 0.042 | |||
| 500 | 0.003 | 0.011 | 0.001 | 0.047 | |||
| 0.84 | 100 | 0.013 | 0.077 | 0.004 | 0.043 | ||
| 250 | 0.012 | 0.087 | 0.000 | 0.041 | |||
| 500 | 0.006 | 0.078 | 0.001 | 0.042 | |||
| 0.8 | 0.67 | 100 | 0.001 | 0.007 | 0.001 | 0.031 | |
| 250 | 0.004 | 0.007 | 0.004 | 0.032 | |||
| 500 | 0.002 | 0.011 | 0.000 | 0.036 | |||
| 0.84 | 100 | 0.003 | 0.015 | 0.001 | 0.032 | ||
| 250 | 0.005 | 0.019 | 0.001 | 0.034 | |||
| 500 | 0.003 | 0.011 | 0.000 | 0.038 | |||
| 0.9 | 1.04 | 100 | 0.000 | 0.002 | 0.002 | 0.026 | |
| 250 | 0.004 | 0.002 | 0.000 | 0.034 | |||
| 500 | 0.000 | 0.001 | 0.000 | 0.037 | |||
| 1.34 | 100 | 0.001 | 0.006 | 0.000 | 0.033 | ||
| 250 | 0.002 | 0.002 | 0.000 | 0.040 | |||
| 500 | 0.003 | 0.006 | 0.003 | 0.046 | |||
| Power | |||||||
| 0.05 | 0.6 | 0.84 | 100 | 0.593 | 0.905 | 0.255 | 0.426 |
| 250 | 0.945 | 0.996 | 0.710 | 0.690 | |||
| 500 | 0.998 | 1.000 | 0.969 | 0.889 | |||
| 0.7 | 0.84 | 100 | 0.801 | 0.942 | 0.499 | 0.462 | |
| 250 | 0.990 | 0.999 | 0.949 | 0.772 | |||
| 500 | 1.000 | 1.000 | 0.997 | 0.945 | |||
| 0.8 | 0.84 | 100 | 0.883 | 0.971 | 0.693 | 0.558 | |
| 250 | 0.998 | 1.000 | 0.998 | 0.868 | |||
| 500 | 1.000 | 1.000 | 1.000 | 1.000 | |||
| 0.9 | 1.04 | 100 | 0.944 | 0.980 | 0.870 | 0.822 | |
| 250 | 1.000 | 1.000 | 0.998 | 0.992 | |||
| 500 | 1.000 | 1.000 | 1.000 | 1.000 | |||
| 0.1 | 0.6 | 0.84 | 100 | 0.916 | 0.988 | 0.713 | 0.836 |
| 250 | 1.000 | 1.000 | 0.991 | 0.984 | |||
| 500 | 1.000 | 1.000 | 1.000 | 1.000 | |||
| 0.7 | 0.84 | 100 | 0.991 | 0.997 | 0.908 | 0.890 | |
| 250 | 1.000 | 1.000 | 1.000 | 0.995 | |||
| 500 | 1.000 | 1.000 | 1.000 | 1.000 | |||
| 0.8 | 0.84 | 100 | 0.994 | 1.000 | 0.975 | 0.970 | |
| 250 | 1.000 | 1.000 | 1.000 | 1.000 | |||
| 500 | 1.000 | 1.000 | 1.000 | 1.000 | |||
| Mis-specified model (logistic model) | |||||||
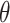
|

|

|
EB | PB | Wald.CV | Fuzzy p-value | |
| Type I error rate | |||||||
| 0 | 0.6 | 100 | 0.031 | 0.139 | 0.012 | 0.072 | |
| 250 | 0.016 | 0.146 | 0.010 | 0.047 | |||
| 500 | 0.016 | 0.165 | 0.005 | 0.046 | |||
| 0.7 | 100 | 0.011 | 0.027 | 0.006 | 0.055 | ||
| 250 | 0.007 | 0.029 | 0.005 | 0.043 | |||
| 500 | 0.008 | 0.034 | 0.001 | 0.045 | |||
| 0.8 | 100 | 0.005 | 0.002 | 0.003 | 0.026 | ||
| 250 | 0.005 | 0.007 | 0.004 | 0.023 | |||
| 500 | 0.003 | 0.002 | 0.009 | 0.027 | |||
| 0.9 | 100 | 0.005 | 0.001 | 0.003 | 0.030 | ||
| 250 | 0.002 | 0.000 | 0.002 | 0.042 | |||
| 500 | 0.002 | 0.000 | 0.002 | 0.044 | |||
| Power | |||||||
| 0.1 | 0.6 | 100 | 0.873 | 0.999 | 0.558 | 0.805 | |
| 250 | 0.996 | 1.000 | 0.884 | 0.967 | |||
| 500 | 1.000 | 1.000 | 0.995 | 0.996 | |||
| 0.7 | 100 | 0.928 | 0.999 | 0.631 | 0.862 | ||
| 250 | 0.995 | 1.000 | 0.927 | 0.981 | |||
| 500 | 1.000 | 1.000 | 0.997 | 1.000 | |||
| 0.8 | 100 | 0.977 | 1.000 | 0.798 | 0.932 | ||
| 250 | 0.999 | 1.000 | 0.942 | 0.989 | |||
| 500 | 1.000 | 1.000 | 1.000 | 1.000 | |||
Table 3.
Coverage of 95% two-sided confidence interval (CI) and corresponding length in the parenthesis using Wald with cross-validation method, under different underlying models and scenarios.  indicates the performance of biomarker
indicates the performance of biomarker 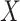 alone and
alone and  indicates the incremental value
indicates the incremental value
| Coverage (length) of two-sided 95% CI | |||||
|---|---|---|---|---|---|
| Correctly specified model (logic model) | |||||

|

|
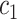
|

|
||
| 100 | 250 | 500 | |||
| 0 | 0.6 | 0 | 98.3% (0.117) | 99.0% (0.053) | 97.8% (0.051) |
| 0.84 | 98.5% (0.123) | 98.8% (0.060) | 98.2% (0.034) | ||
| 0.7 | 0 | 98.0% (0.056) | 96.8% (0.019) | 95.9% (0.008) | |
| 0.84 | 97.3% (0.071) | 97.9% (0.030) | 97.8% (0.015) | ||
| 0.8 | 0.67 | 95.5% (0.036) | 95.1% (0.014) | 95.2% (0.007) | |
| 0.84 | 96.0% (0.040) | 95.2% (0.016) | 95.6% (0.008) | ||
| 0.9 | 1.04 | 92.2% (0.023) | 93.1% (0.009) | 93.9% (0.005) | |
| 1.34 | 95.1% (0.026) | 94.2% (0.011) | 93.5% (0.006) | ||
| 0.05 | 0.6 | 0.84 | 94.3% (0.154) | 96.0% (0.089) | 96.5% (0.056) |
| 0.7 | 0.84 | 93.8% (0.108) | 96.4% (0.060) | 95.5% (0.039) | |
| 0.8 | 0.84 | 92.2% (0.083) | 94.7% (0.049) | 94.9% (0.033) | |
| 0.9 | 1.04 | 91.7% (0.069) | 93.4% (0.042) | 94.0% (0.029) | |
| 0.1 | 0.6 | 0.84 | 95.4% (0.175) | 95.7% (0.100) | 96.9% (0.065) |
| 0.7 | 0.84 | 95.3% (0.128) | 95.6% (0.074) | 95.7% (0.049) | |
| 0.8 | 0.84 | 94.5% (0.105) | 94.5% (0.063) | 95.3% (0.043) | |
| Mis-specified model (logistic model) | |||||

|

|

|
|||
| 100 | 250 | 500 | |||
| 0 | 0.6 | 98.3% (0.121) | 99.0% (0.062) | 98.4% (0.036) | |
| 0 | 0.7 | 98.1% (0.074) | 97.5% (0.032) | 98.3% (0.017) | |
| 0 | 0.8 | 96.2% (0.044) | 96.0% (0.019) | 96.0% (0.010) | |
| 0 | 0.9 | 93.5% (0.025) | 94.6% (0.011) | 93.8% (0.005) | |
| 0.1 | 0.6 | 93.4% (0.212) | 93.3% (0.137) | 95.0% (0.097) | |
| 0.1 | 0.7 | 91.9% (0.189) | 92.9% (0.120) | 94.9% (0.084) | |
| 0.1 | 0.8 | 93.0% (0.156) | 94.0% (0.099) | 95.1% (0.069) | |
From Table 1 below and Table 1 in the supplementary material available at Biostatistics online, under both correctly specified and mis-specified underlying models, we see that the naïve estimator could overestimate the new biomarker’s performance when sample size is small. When the true incremental value is small, the overestimation issue becomes less severe as sample size increases, as well as for settings with better performance of  alone (i.e., settings with larger
alone (i.e., settings with larger  value). Using cross-validation in general corrects this overestimation problem and can lead to small attenuation in some settings.
value). Using cross-validation in general corrects this overestimation problem and can lead to small attenuation in some settings.
From Table 2, when the null hypothesis is true, the test based on PB often has inflated Type I error, whereas the corresponding test based on EB typically has Type I error rate smaller than the nominal level (e.g., when biomarker  itself has good performance). The test based on Wald.CV in general tends to be more conservative than EB. The fuzzy p-value method works reasonably well with Type I error fairly close to the nominal level for all settings considered. When the alternative hypothesis is true, the test based on EB generally has better or comparable power compared with other tests; the performance of Wald.CV and the fuzzy p-value method are more or less comparable to each other and their relative performance varies across settings.
itself has good performance). The test based on Wald.CV in general tends to be more conservative than EB. The fuzzy p-value method works reasonably well with Type I error fairly close to the nominal level for all settings considered. When the alternative hypothesis is true, the test based on EB generally has better or comparable power compared with other tests; the performance of Wald.CV and the fuzzy p-value method are more or less comparable to each other and their relative performance varies across settings.
From Table 3 and Table 1 in the supplementary material available at Biostatistics online, for the purpose of constructing two-sided CI for the incremental value, the Wald.CV approach is satisfactory for both underlying models. It clearly shows that the Wald.CV two-sided CIs have coverage either close to or slightly larger than the nominal level. Under the mis-specified model and alternative hypothesis, although the two-sided CIs can have slight undercoverage for the smaller sample size, their coverage approaches the nominal level as when the sample size is large enough, i.e.,  .
.
Overall, we observe a similar pattern on performance comparison among different approaches under the (correctly specified) logic and (mis-specified) logistic risk models. For testing the significant incremental value of a new biomarker, the one-sided test based on empirical bootstrap CI is recommended; the fuzzy p-value approach is also desirable, given its theoretical foundation and reasonable performance. For making inference about the uncertainty of 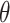 estimator, the Wald CI based on the cross-validated estimator is desired for constructing two-sided CI about
estimator, the Wald CI based on the cross-validated estimator is desired for constructing two-sided CI about 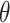 .
.
4. Pancreatic cancer study
In this section, we apply the proposed methods to a real data example from a pancreatic cancer study aimed at identifying biomarkers for early detection of pancreatic cancer. In this study, plasma samples were collected from  patients with pancreatic cancer and
patients with pancreatic cancer and 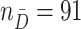 healthy individuals for biomarker measurement (Tang and others, 2015). The sLeA glycan, on which the CA19-9 assay is based, is currently the only established biomarker for pancreatic cancer detection. However, its performance for early detection of pancreatic cancer is not satisfactory given that it is not elevated in about 25% of pancreatic cancers. Tang and others (2015) found that sialyl-Lewis X (sLeX), a structural isomer of sLeA, was elevated in the plasma of 14–19% of patients with low sLeA. Thus, a biomarker panel combining sLeA and sLeX can potentially be useful in the clinical detection of pancreatic cancer. In this study, the estimated optimal average sensitivity and specificity based on sLeA alone is 0.683 (0.636 after cross-validation). Here, we estimate the incremental value of sLeX when combined with sLeA using an OR rule and test the hypothesis that a strategy combining the two biomarkers performs better than using the sLeA biomarker alone. The estimated naïve and cross-validated incremental values of sLeX are 0.079 and 0.062, respectively. We apply the EB, PB, and Wald.CV methods to conduct a one-sided test for incremental value of sLeX. We also apply the fuzzy p-value approach to the data and compute the average rejection rate over 1000 random draws. In addition, the two-sided CI is constructed based on Wald.CV.
healthy individuals for biomarker measurement (Tang and others, 2015). The sLeA glycan, on which the CA19-9 assay is based, is currently the only established biomarker for pancreatic cancer detection. However, its performance for early detection of pancreatic cancer is not satisfactory given that it is not elevated in about 25% of pancreatic cancers. Tang and others (2015) found that sialyl-Lewis X (sLeX), a structural isomer of sLeA, was elevated in the plasma of 14–19% of patients with low sLeA. Thus, a biomarker panel combining sLeA and sLeX can potentially be useful in the clinical detection of pancreatic cancer. In this study, the estimated optimal average sensitivity and specificity based on sLeA alone is 0.683 (0.636 after cross-validation). Here, we estimate the incremental value of sLeX when combined with sLeA using an OR rule and test the hypothesis that a strategy combining the two biomarkers performs better than using the sLeA biomarker alone. The estimated naïve and cross-validated incremental values of sLeX are 0.079 and 0.062, respectively. We apply the EB, PB, and Wald.CV methods to conduct a one-sided test for incremental value of sLeX. We also apply the fuzzy p-value approach to the data and compute the average rejection rate over 1000 random draws. In addition, the two-sided CI is constructed based on Wald.CV.
When using the original data set, the one-sided tests based on EB and PB both reject the null hypothesis with lower limits of one-sided CI for incremental value of sLeX being 0.022 and 0.042, respectively, while the Wald.CV method fails to do so (p-value  0.093). This finding is not surprising, given that EB and PB have been shown to be more powerful compared with Wald.CV. The fuzzy p-value approach rejects the null hypothesis with probability 0.67. The two-sided CI derived using Wald.CV is
0.093). This finding is not surprising, given that EB and PB have been shown to be more powerful compared with Wald.CV. The fuzzy p-value approach rejects the null hypothesis with probability 0.67. The two-sided CI derived using Wald.CV is  .
.
Moreover, to investigate the impact of increased sample size, we generate a larger dataset by randomly drawing 200 cases and 200 controls with replacement from the original data and apply our proposed methods. With the larger sample sizes, the one-sided CIs of incremental value based on EB and PB have lower limits 0.062 and 0.049, respectively, and the one-sided Wald.cv test has p-value  , providing strong evidence that adding sLeX yields significantly better performance compared with using sLeA alone. The fuzzy p-value approach rejects the null hypothesis with probability 1. The Wald.CV two-sided CI for incremental value of sLeX equals
, providing strong evidence that adding sLeX yields significantly better performance compared with using sLeA alone. The fuzzy p-value approach rejects the null hypothesis with probability 1. The Wald.CV two-sided CI for incremental value of sLeX equals  .
.
5. Concluding remarks
In this paper, we considered an inference problem about the incremental value of a new biomarker when combined with an established biomarker using an OR rule, motivated by the example in early detection of pancreatic cancer, where the standard biomarker CA19-9 is only elevated in a subclass of cancer cases. Thus, identifying a new biomarker that is present in the other subclasses to combine with CA19-9 is of primary interest. We considered a nonparametric estimator of incremental value of the new biomarker, based on an estimator of the OR rule that maximizes the weighted average of sensitivity and specificity. We proposed different procedures based on bootstrap, cross-validation, and a novel fuzzy p-value approach, to test and make inference about a new biomarker’s incremental value. Through extensive numerical studies, we found that the hypothesis test based on one-sided empirical bootstrap CI has satisfactory performance in terms of well-controlled Type I error rate and decent power for declaring the usefulness of the new marker, while the popular percentile bootstrap CI should be avoided due to its inflated Type I error rate. When it is of interest to provide uncertainty about the estimated incremental value, we found that two-sided Wald-type CI based on cross-validated estimates of incremental value performs very well, with coverage close to the nominal level. The novel fuzzy p-value method we proposed for testing the incremental value also has satisfactory performance. Moreover, the fuzzy p-value method can be particularly appealing as a testing procedure given its theoretical foundation and its potential to be extended to other biomarker testing problems when non-regularity is an issue. Importantly, our findings are based not only on settings where the true risk model conditional on biomarkers follows a logic model with an OR combination. They are also based on settings where the logic risk model does not hold, but the OR rule is used as a practical way to combine biomarkers for simplicity and interpretability. Our findings provide valuable guidance on selecting appropriate methods for testing and making inference about the incremental value of a new biomarker. Such threshold-based decision rules are of interest not only in the specific classification problems we considered here, but also in other problem settings such as the identification of optimal dynamic treatment regimens (Laber and Zhao, 2015; Wang and Rudin, 2015; Zhang and others, 2015), where the decision is to predict optimal treatment allocation instead of disease/non-disease status.
We used grid search to identify the threshold parameters. Though not a focus of this work, a computationally efficient implementation could find  in
in  time by first sorting
time by first sorting  , and subsequently using cumulative sums to iteratively compute the
, and subsequently using cumulative sums to iteratively compute the 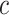 -specific weighted combination of sensitivity and specificity. An analogous
-specific weighted combination of sensitivity and specificity. An analogous  time procedure could be used to derive
time procedure could be used to derive  and
and  by fixing a candidate
by fixing a candidate  , again sorting
, again sorting  , and iteratively computing the
, and iteratively computing the  -specific sum at different values of
-specific sum at different values of 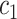 . Repeating this over all
. Repeating this over all 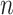 candidate values for
candidate values for  will find the maximizer.
will find the maximizer.
Furthermore, it is worth mentioning that while our current work focuses on the estimation and inference of the incremental value of a new single biomarker, the framework could be in general extended to make inference about the incremental value raised by multiple new biomarkers. Let  be an established biomarker for predicting the disease outcome
be an established biomarker for predicting the disease outcome  and let
and let  be the
be the  new biomarkers where
new biomarkers where  is an integer. When combining the new biomarkers
is an integer. When combining the new biomarkers  with the established biomarker
with the established biomarker  , we suppose a case is declared if either one of
, we suppose a case is declared if either one of 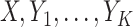 is elevated. The sensitivity and specificity using the OR rule combining
is elevated. The sensitivity and specificity using the OR rule combining  with
with  are defined as
are defined as  and
and 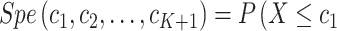
 , respectively, for some thresholds
, respectively, for some thresholds 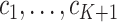 . Notice that the problem considered in this article is the case with
. Notice that the problem considered in this article is the case with  . Our current framework under
. Our current framework under 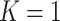 can be naturally applied to the scenarios with multiple new biomarkers, i.e.,
can be naturally applied to the scenarios with multiple new biomarkers, i.e.,  . More generally the method could extend to include both OR/AND combinations. When the number of markers to be combined is increased, one might consider other algorithms such as LOGIC regression or tree-based algorithms, which are more computationally efficient than the grid search method in finding the maximizers
. More generally the method could extend to include both OR/AND combinations. When the number of markers to be combined is increased, one might consider other algorithms such as LOGIC regression or tree-based algorithms, which are more computationally efficient than the grid search method in finding the maximizers 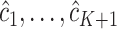 of the weighted average of empirical estimates of sensitivity and specificity.
of the weighted average of empirical estimates of sensitivity and specificity.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
6. Software
The R code is available at https://github.com/WangLu88/ORrules.git.
Funding
This work was supported by the U.S. National Institutes of Health grant R01 GM106177-01.
References
- Bcaker S. G. (2000). Identifying combinations of cancer markers for further study as triggers of early intervention. Biometrics 56, 1082–1087. [DOI] [PubMed] [Google Scholar]
- Bickel P. J., Klaassen C. A., Bickel P. J., Ritov Y., Klaassen J., Wellner J. A. and Ritov Y. A. (1998). Efficient and Adaptive Estimation for Semiparametric Models, Volume 2 New York: Springer New York. [Google Scholar]
- Efron B. and Tibshirani R. J. (1994). An Introduction to the Bootstrap. Boca Raton: CRC press. [Google Scholar]
- Etzioni R., Kooperberg C., Pepe M., Smith R. and Gann P. H. (2003). Combining biomarkers to detect disease with application to prostate cancer. Biostatistics 4, 523–538. [DOI] [PubMed] [Google Scholar]
- Feng Z. (2010). Classification versus association models: should the same methods apply? Scandinavian Journal of Clinical and Laboratory Investigation 70, 53–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gann P. H., Ma J., Catalona W. J. and Stampfer M. J. (2002). Strategies combining total and percent free prostate specific antigen for detecting prostate cancer: a prospective evaluation. The Journal of Urology 167, 2427–2434. [PubMed] [Google Scholar]
- Geyer C. J. and Meeden G. D. (2005). Fuzzy and randomized confidence intervals and p-values. Statistical Science 20, 358–366. [Google Scholar]
- Han J., Pei J. and Kamber M. (2011). Data Mining: Concepts and Techniques. Burlington: Elsevier. [Google Scholar]
- Laber E. B. and Zhao Y. Q. (2015). Tree-based methods for individualized treatment regimes. Biometrika 102, 501–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntosh M. W. and Pepe M. S. (2002). Combining several screening tests: optimality of the risk score. Biometrics 58, 657–664. [DOI] [PubMed] [Google Scholar]
- Ruczinski I., Kooperberg C. and LeBlanc M. (2003). Logic regression. Journal of Computational and Graphical Statistics 12, 475–511. [Google Scholar]
- Tang H., Singh S., Partyka K., Kletter D., Hsueh P., Yadav J., Ensink E., Bern M., Hostetter G., Hartman D.. and others (2015). Glycan motif profiling reveals plasma sialyl-lewis X elevations in pancreatic cancers that are negative for sialyl-lewis A. Molecular & Cellular Proteomics 14, 1323–1333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Vaart A. W. (1998). Asymptotic Statistics, Volume 3 Cambridge: Cambridge University Press. [Google Scholar]
- Wang F. and Rudin C. (2015). Falling rule lists. In Proceedings of the 18th International Conference on Artificial Intelligence and Statistics, PMLR 38, 1013–1022. [Google Scholar]
- Youden W. J. (1950). Index for rating diagnostic tests. Cancer 3, 32–35. [DOI] [PubMed] [Google Scholar]
- Zhang Y., Laber E. B., Tsiatis A. and Davidian M. (2015). Using decision lists to construct interpretable and parsimonious treatment regimes. Biometrics 71, 895–904. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



