Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Jun 12;5(24):14689–14701. doi: 10.1021/acsomega.0c01444

Shaking-Induced Aggregation and Flotation in Immunoglobulin Dispersions: Differences between Water and Water–Ethanol Mixtures

Nikolai F Bunkin †,‡,*, Alexey V Shkirin ‡,§, Barry W Ninham ∥, Sergey N Chirikov §, Leonid L Chaikov ⊥, Nikita V Penkov #, Valeriy A Kozlov †,‡, Sergey V Gudkov ‡
PMCID: PMC7315612  PMID: 32596606

Abstract

graphic file with name ao0c01444_0021.jpg

Structural characterization by three complementary methods of laser diagnostics (dynamic light scattering, laser phase microscopy, and laser polarimetric scatterometry) has established that shaking of immunoglobulin G (IgG) dispersions in water and ethanol–water mixtures (36.7 vol %) results in two effects. First, it intensifies the aggregation of IgG macromolecules. Second, it generates bubbles with a size range that is different in each solvent. The aggregation is enhanced in ethanol–water mixtures because of IgG denaturation. IgG aggregates have a size of ∼300 nm in water and ∼900 nm in ethanol–water mixtures. The flotation of IgG is much more efficient in water. This can be explained by a better adsorption of IgG particles (molecules and aggregates) on bubbles in water as compared to ethanol–water mixtures. Bulk nanobubbles and their association with IgG aggregates were visualized by laser phase microscopy in water but were not detected in ethanol–water mixtures. Therefore, the nanobubble flotation mechanism for IgG aggregates acting in water is not feasible for ethanol–water mixtures.

1. Introduction

A number of technologies involve the effects of mechanical impacts on water and aqueous solutions. In some cases, mechanical impacts can lead to a significant acceleration of various chemical and physical processes.1−5 Vibration treatment, in particular, shaking, is widely used in technological procedures, typically those that require fluid mixing to enhance dissolution of chemical compounds. Another example is reaching ultralow concentrations with the use of sequential dilutions.

In this study, the effects of shaking are explored for dispersions of large protein macromolecules, immunoglobulin G (IgG), in two different media: water and an ethanol–water mixture (EWM). It is worth noting that ethanol (36.7 vol %) is one of the pharmacopoeial alcohols used in pharmaceutics.6 It is known that shaking IgG solutions enhances the natural aggregation of IgG molecules7,8 and can change the morphology of protein aggregates, used for therapeutic purposes.9 In addition to aggregation, shaking has another effect: the flotation of IgG molecules and aggregates due to their attachment to bubbles and stabilization of bubbles. Shaking-induced flotation gives results similar to electroflotation, where bubbles are also formed during electrolysis. Electroflotation is used in food technology to extract proteins from multicomponent aqueous mixtures.10

Flotation is efficient provided that the floating bubbles have a sufficient lifetime for particle-bubble adhesion to occur.11−15 Here, the size of bubbles plays a key role because even micron-sized bubbles have insufficient lifting power and the same being true a fortiori for nanobubbles. Nanobubbles are incapable of rising in water because of their almost neutral buoyancy.16,17 This is because they are metastable, “dressed” with impurities, or with surfactants or adsorbed salt. However, they can aggregate with suspended colloidal particles and thereby act as “secondary collectors”, thereby, improving particle flotation.18,19 In addition, nanobubbles can serve as nuclei (“seeds”) for the adhesion of particles on coarser bubbles, including macrobubbles (>100 μm in diameter), see ref (20). In the same way, we can expect equally that sufficiently stable nanobubbles can be the source of depletion forces to inhibit bubble–bubble fusion.21−23 Furthermore, it can be shown that charged nanobubbles with adsorbed proteins provide a stabilizing double layer force between the macrobubbles, just as micelles stabilize microemulsion or emulsion drops. This is, of course, counterintuitive, but the situation with bubbles is quite analogous to charged micelles.24,25

To summarize, the combination of nanobubbles, microbubbles, and macrobubbles provides a bewildering complex and highly organized “soup”. It can lead to capture of colloidal particles, that is, nanobubbles enhance the attachment of these particles to larger bubbles and thus increase the flotation efficiency, or vice versa, depending on protein surface hydrophobicity and charge. Control of these processes is the main game.

Nanobubbles, being stable or not, are effectively nucleated by stirring.26,27 One consequence of shaking is that the layers of liquid adjacent to the vial surfaces have a lower speed relative to more distant layers. Close to the vial side, the liquid is completely immobile. Because of this inequality of the velocities of neighboring layers, discontinuities in the liquid inevitably arise. These discontinuities are filled with gas molecules and the process opposes the instantaneous collapse of the cavities formed. Chaotropic (structure-breaking) ions are capable of adsorbing on the internal surface of the cavity.28 This could lead to the appearance of electrical charge on the surface (note that some amount of external ionic impurity is always present in purified water anyway). Furthermore, the process of adsorption and desorption of these ions on the charged surface eventually results in the formation of a stable gas bubble with diameters ∼300 nm. We have termed such structures “bubstons”, that is, bubbles stabilized by ions.27−29

The IgG dispersions were analyzed by laser methods: dynamic light scattering (DLS), laser phase microscopy (LPM), and laser polarimetric scatterometry (LPS). The techniques are described in detail, for example, in refs.27,30 The joint use of these methods enabled us to detect and characterize particles with greater or less information and accuracy at very wide scales ranging from ∼1 to 104 nm.

2. Results and Discussion

2.1. Nanobubble Generation by Shaking: Comparison of Pure Water and an EWM

From the Introduction, it can be concluded that vigorous shaking should produce gas nanobubbles in aqueous media. In the literature, nanobubbles are understood to mean long-lived gas-filled cavities with a diameter of less than a micron. As was recently shown,26 nanometer-sized oxygen bubbles could be produced by vibration, and their concentration and size distribution were measured by nanoparticle tracking analysis. It turned out that the concentration of bulk nanobubbles largely increases after vibration treatment and is determined by the vibration frequency and time. Here, we also studied the influence of shaking on the volume number density of gas nanobubbles in water and a water–ethanol mixture.

We performed DLS measurements in water before and immediately after shaking (see Figure 1). The component at 0.5 nm can be associated with short-lived ice-like clusters consisting of ∼4–5 water molecules that are included in the first coordination sphere (hydration shell, see, e.g., ref (31)). The component at 250 nm is related to the bubston phase. This is also supported by LPM data (see Figure 2).

Figure 1.

Figure 1

Open in a new tab

DLS intensity distribution over the particle sizes in water: before shaking (blue solid curve) and immediately after shaking (red dashed curve). Total scattering intensities are Itot(173°) = 12 kcps (0.5 nm—62.2%, 250 nm—37.8%) and Itot(173°) = 40 kcps, correspondingly.

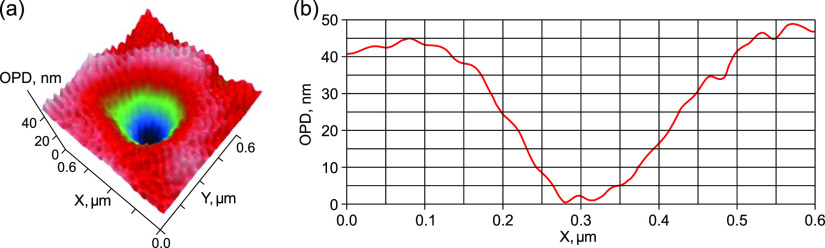
Figure 2.

Figure 2

Open in a new tab

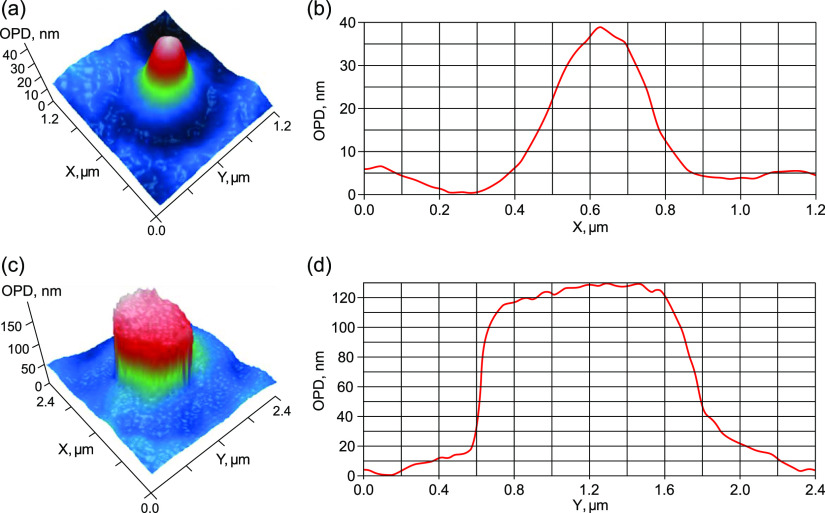
LPM images of a bubston with d ≈ 250 nm in water after shaking: (a) 2D distribution of the optical path difference (OPD) and (b) 1D profile, Δh = −20 nm.

Figure 2a shows two-dimensional (2D) distribution of the optical phase shift across a separate bubston with a size of ≈250 nm (the half-height estimate). Exactly the same size was measured by DLS both before and after shaking. Figure 5b shows a one-dimensional (1D) profile drawn through the center of the bubston.

Figure 5.

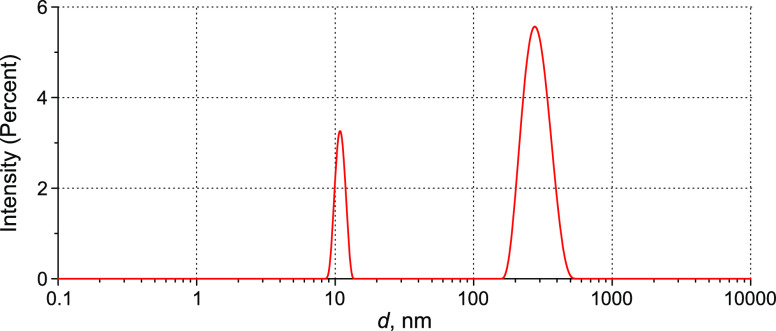
Figure 5

Open in a new tab

DLS intensity distribution over the particle sizes in aqueous IgG solution with volume number density 3 × 1014 cm–3 before shaking. Average total intensity (minus background scattering) Itot(173°) = 255 kcps (12 nm peak is 18.2% and 300 nm peak is 81.8%).

From the distribution shown in Figure 1, it is possible to evaluate the change in the volume number density of the bubstons immediately after shaking. The percentage ratio of the peak intensities at 250 nm before and after shaking gives the value 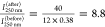Inline graphic, which is equal to the ratio of the nanobubble number density after/before shaking. A similar increase in the volume number density of nanobubbles after shaking is observed in ref (26).

In Figure 3, we exhibit the results of DLS measurements in an EWM before and immediately after shaking. In this case, the ratio of the scatterer number density is Inline graphic, that is, the number of scatterers per volume remains the same.

Figure 3.

Figure 3

Open in a new tab

DLS intensity distribution over the particle sizes in an EWM: before shaking (blue solid curve) and immediately after shaking (red dashed curve). Total scattering intensities are Itot(173°) = 80 kcps and Itot(173°) = 85 kcps, correspondingly.

Figure 4 shows a characteristic 2D distribution and the corresponding 1D profile for 150 nm inhomogeneities observed in the initial water–ethanol solution. The height of the profile Δh makes it possible to assign the observed inhomogeneities to mesodroplets enriched with ethanol, see our recent studies.32,33 However, we cannot exclude that in that case, we deal with artifacts associated with interference noise.34 Thus, we conclude that in this case, the scatterers are liquid mesodroplets, whose volume number density is not changed in the process of shaking.

Figure 4.

Figure 4

Open in a new tab

LPM images of a mesoscale particle with a size of d ≈ 150 nm, presumably, an ethanol-enriched mesodroplet in an unshaken EWM: (a) 2D distribution of the OPD and (b) 1D profile of this particle, Δh ≈ 7 nm.

In this regard, it is worth mentioning the study,35 where it is claimed that when ethanol is added to water, the volume number density of gas nanobubbles increases compared to aqueous samples treated with a continuous high-shear rotor-stator device, that is, actually after vigorous vibrations. The authors35 conclude that there are no nanodroplets of alcohol in the water–alcohol mixture and they observed gas nanobubbles, but this conclusion is based on indirect data because the nanoparticle tracking analysis method used in ref (35) is unable to distinguish between a nanodroplet and a nanobubble. At the same time, using the phase microscopy technique, which allows us to directly distinguish gas nanobubbles from nanodroplets, we did not find gas nanobubbles in water-alcohol mixtures.

2.2. Solution of IgG in Water: Characterization of IgG Aggregates

Figure 5 depicts the results of DLS experiments in aqueous IgG solution, with the volume number density of IgG macromolecules being 3 × 1014 cm–3. The size distribution consists of two peaks: a peak at 12 nm can be associated with monomeric IgG molecules.36 We believe that the 300 nm peak is related chiefly to IgG aggregates. In this figure, we exhibit the average total intensity, from which the Rayleigh scattering (IR(173°) ≈ 10 kcps) is subtracted, Itot(173°) = 255 kcps. The peak at 300 nm amounts to 81.8% of the total intensity, while the 12 nm peak is related to 18.2% of the total intensity. We also measured the average intensity of the scattered light I(θ) at a scattering angle of θ = 173°, which allows us to estimate the volume number density of scatterers α in accordance with eq 7 (see Section 6.1) provided that the scattering cross section Csca and scattering indicatrix F(θ) of single scatterer are known. Representation of monomeric IgG molecules as spheres with a size of 12 nm allows us to calculate Csca = 0.27 × 10–10 μm2 and F(173°) = 1.49; thus, for the monomers, we have α = 2.4 × 1014 cm–3. This is in good agreement with the nominal concentration of the solution, see Section 4. By calculation for the particles with a size of 300 nm (assuming their sphericity) Csca = 0.2193 × 10–2 μm2 and F(173°) = 0.37, we obtain α = 5.4 × 107 cm–3.

For the volume number density of such mesodroplets shown in Figures 3 and 4, in accordance with eq 7, we obtain α ≈ 109 cm–3. It is important that small hydrophobic particles can play the role of nucleation centers for self-assembly of organic liquid molecules, which gives rise to the mesodroplet generation,37 that is, some IgG molecules can be encapsulated into ethanol mesodroplets.

In Figure 6, the results obtained by LPM are presented. Panel (a) shows the 2D distribution of the optical phase shift across two closely located particles with a size of 300 nm; particles of this size were also detected in the DLS experiment. Panel (b) shows the 1D profile of these particles, which was drawn through their centers. The phase profile of 300 nm solid particles (Figure 6b) allows us to estimate its refractive index as n = 1.5 ± 0.02 according to the calibration curve (see Section 5.3). Refractive index measurements for various proteins38 show that they typically have n ≥ 1.53 (being proteins, IgGs are assumed to obey this inequality). Therefore, a rather low value of n measured by LPM indicates that we most likely deal with 300 nm aggregates of individual IgG molecules with a size of ∼12 nm, separated by water monolayers. The fractal properties of these aggregates were investigated with the help of the scattering matrix technique (see below). Note that the observed convergence of submicron IgG aggregates can be the initial stage of the macroaggregate formation, which is typical for proteins.

Figure 6.

Figure 6

Open in a new tab

LPM images of inhomogeneities in aqueous IgG solution before shaking: (a) 2D distribution of the OPD for particles with a size of about 300 nm and (b) 1D profile of this distribution, Δh ≈ 25 nm.

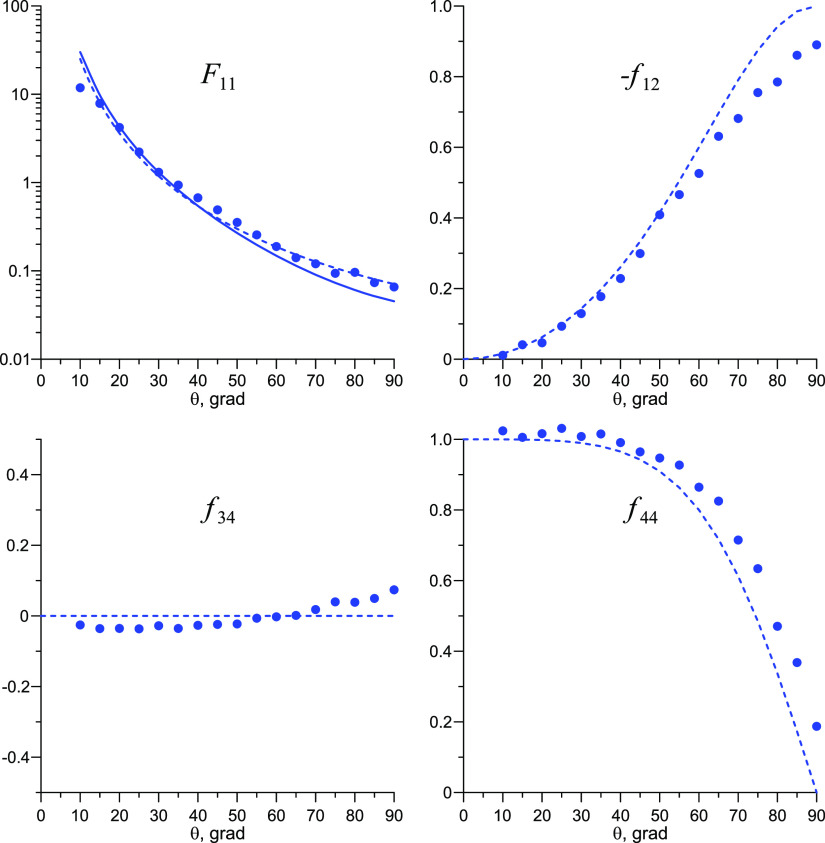
To make sure that IgG aggregation indeed takes place and to determine the fractal dimensions of the aggregates, the angular dependences of the scattering matrix elements for the IgG solution were measured. The knowledge of the fractal dimension allows one to determine the type of monomer aggregation.39 The experimental data were compared with theoretical dependences calculated using the T-matrix method.40 As was shown in that work, the analysis of the angular dependences of the scattering matrix elements allows us to find the size distribution of particles, provided that the size does not exceed the radiation wavelength.

In the case where the size of particles exceeds the wavelength, we can find out whether these particles are “monolithic” or clustered particles having a fractal inner structure.39 For an isotropic medium with randomly oriented scatterers, the 4 × 4 scattering matrix F(θ) has a block-diagonal form:41 the elements F14, F41, F24, F42, F31, F32, F13, and F23 are zero, F12 = F21, and F34 = −F43. In addition, for spherical particles, we have F33 = F44 and F22 = 1. Summarizing, the scattering matrices of media with spherical particles are completely described by the angular dependences F11(θ), F12(θ), F34(θ), and F44(θ).

In Figure 7, we show the experimental and theoretical angular dependences of the scattering matrix elements for the initial aqueous IgG solution with volume number density 3 × 1014 cm–3. The matrix element values, measured at θ < 10° and θ > 90°, are not given because of the contribution of distorting factors, for example, reflection from the vial sides. Here, fij(θ) = Fij(θ)/F11(θ) are the normalized elements; F11(θ) describes the scattering indicatrix. The dependencies f12(exp) (θ), f34 (θ), and f44(exp) (θ) are similar to those for Rayleigh scattering (dashed lines), while the dependence F11 (θ) for the IgG solution at large angles is well-described by the expression A0(sin(θ/2))−Df (dashed line), where A0 is a constant. A scattering matrix of this type is characteristic for the media containing clusters, whose monomers (IgG macromolecules, in our case) have a size much smaller than the radiation wavelength. Df means the fractal dimension of the cluster41 (see Section 6.2). Slight deviations of f12(exp) (θ), f34 (θ), and f44(exp) (θ) from the elements of the Rayleigh scattering matrix at large angles are apparently because of multiple scattering.

Figure 7.

Figure 7

Open in a new tab

Dependences of the scattering matrix elements F11(θ), f12(θ), f34(θ), and f44(θ) measured via LPS in aqueous IgG solution before shaking. The circles are experimental points, the solid line is the theoretical approximation by multitype spherical particles, and the dashed line is the Rayleigh–Gans–Debye approximation for the IgG aggregates. F11(exp) (θ) is plotted so that F11 (30°) = F11(theor) (30°); for more detail, see ref (40).

The element F11theor(θ) calculated in accordance with eq 8 (Section 6.2) is shown in Figure 7 (solid black curves). The fractal dimension estimated using eq 9 for the IgG aggregates in aqueous solution is Df = 2.7. Such values are typical for the aggregation mechanism according to the “monomer–cluster” scenario.42 As follows from these diagrams, noticeable discrepancies between the theoretical approximation and the experimental results are observed at θ < 20°, where the condition qRg > 1 does not hold.

2.3. IgG Flotation Efficiency with Shaking Aqueous Solutions

Figure 8 shows the scatterer size distribution of DLS intensity in the initial aqueous IgG solution immediately after shaking. Because in this experiment, the scattering volume was fixed at a level of half-height of the cell with liquid, the results are related to the bulk of the liquid sample.

Figure 8.

Figure 8

Open in a new tab

DLS intensity distribution over the particle sizes in aqueous IgG solution with volume number density 3 × 1014 cm–3 immediately after shaking. Average total intensity (background scattering is subtracted) Itot(173°) = 844 kcps (12 nm peak is 4.8%, 250 nm peak is 45.1%, 600 nm peak is 30.5%, and 3000 nm peak is 19.6%).

As seen in Figure 8, immediately after shaking, particles with a mean size d ≈ 200, 600, and 3000 nm are formed. In accordance with our previous results,27,28 scatterers with diameters of 200–300 nm correspond to bubstons; the same size can relate to IgG aggregates (see Figures 6 and 8). Because bubstons are effectively negatively charged,27,28 they can form complexes with IgG aggregates. The peak centered at 600 nm apparently corresponds to small clusters consisting of IgG aggregates and bubstons (in particular, dimers), while the peak at 3000 nm is associated with larger “bubston–IgG aggregate” complexes and/or micron-sized bubbles stabilized by IgG absorbed on its surface.43,44 All these types of particles can adhere to larger micro- and macrobubbles and, thereby, float to the liquid surface.

As follows from the comparison of the diagrams in Figures 5 and 8, the area of the peak corresponding to the IgG molecules of 12 nm in size decreased. During the experiment, the cell was sealed, that is, the total amount of IgG in the liquid could not decrease. Thus, the only mechanism leading to the redistribution of IgG molecules between the bulk liquid and free surface is flotation: IgG molecules together with IgG aggregates are transferred by floating bubbles from the bulk to the surface of the liquid.

We define the flotation coefficient for IgG molecules as Km = (I0(m) – I(m))/I0 = 1 – I(m)/I0(m) = 1 – 40.5/46.4, where I0 and I(m) are the peak intensities (measured in count rate units) at ∼10 nm in the distributions, as shown in Figures 5 and 8, that is, before and after shaking, respectively. The change in IgG amount due to flotation is given by the formula ΔN = N0 – N = Km·N0. On the basis of the diagrams shown in Figures 5 and 8, we arrive at Km ≈ 0.13. This is an upper estimate because some of the individual IgG molecules were aggregated by shaking, and, most likely, not all newly formed IgG aggregates were captured by flotation.

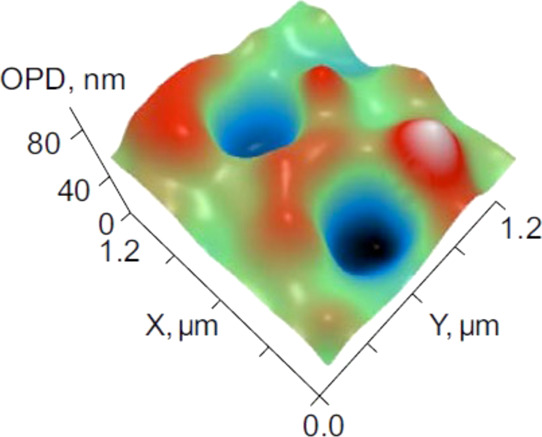
The fact that the agglomerates of IgG aggregates and bubbles do exist was confirmed by the LPM study of a foam sample, taken via a pipette from the surface of the initial IgG solution immediately after shaking. In Figure 9, we give typical patterns of the 2D distribution of OPDs (and the corresponding 1D profiles) for particles inside the foam. As follows from the diagrams, we are dealing with composite particles having simultaneously a concave profile (in accordance with eq 1, such particles are gas bubbles) and a convex profile (particles, whose refractive index exceeds that of water). Figure 9a,b shows a bubble with a size of 400 nm (estimated at the level of half-height of a concave part of the profile), which forms a dimer with a solid particle (most likely, IgG aggregates). The profile is somewhat broadened because of Brownian motion, that is, the real particle size of the dimer is smaller. Figure 9c,d shows an agglomerate of nanobubbles and IgG aggregates. The structures imaged at Figure 9 sustain the model,43 considering the adsorption of protein molecules at the bubble interface to be followed by surface denaturation of these macromolecules and their subsequent aggregation. This means that the bubble surface is covered by IgG aggregates rather than single protein macromolecules.44

Figure 9.

Figure 9

Open in a new tab

Characteristic LPM images (2D distributions of the OPD and the corresponding 1D profiles) of particles in a sample taken from the surface of the initial aqueous IgG solution (volume number density 3 × 1014 cm–3) immediately after shaking: (a,b) nanobubble–IgG aggregate dimer and (c,d) agglomerate of nanobubbles and IgG aggregates.

As far as we cannot estimate correctly the volume number density of IgG aggregates in the bulk immediately after shaking, we should employ a protocol, different from that of IgG monomers, in determining the flotation coefficient Ka for these aggregates. Specifically, to estimate Ka, we have determined the amount of IgG aggregates that appeared on the surface of IgG solution as a result of shaking by measuring the volume concentration of IgG aggregates in 100-fold dilution of an aliquot taken from the surface of the shaken solution. The scattering intensity distribution measured by DLS in the diluted shaken solution is shown in Figure 10. In this diagram, we do not see the peak corresponding to monomeric IgG molecules with a size of 12 nm. Indeed, we can express the volume number density of IgG molecules in the diluted shaken solution in the number of photocounts per time units. Bearing in mind that in the initial solution, N0 = 46.4 kcps (see the comments to Figure 5) and Km ≈ 0.13, we have the estimate N1 = 46.4·Km ≈ 6 kcps, which is lower than the Rayleigh baseline (10 kcps), and therefore, the corresponding peak is hard to resolve. Another possible reason for the invisibility of the peak of monomers is their aggregation/adhesion on the surface of micron-sized bubbles. At the same time, a peak at 300 nm, which is evidently related to IgG aggregates, is clearly visible. In addition, one can see a peak in the region of several microns, which is most likely associated with micron-sized bubbles.

Figure 10.

Figure 10

Open in a new tab

DLS intensity distribution over the particle sizes in 100-fold dilution of shaken aqueous IgG solution (the initial concentration 3 × 1014 cm–3). Average total intensity (minus background scattering) Itot(173°) = 21 kcps (250 nm peak is 62% and 3000 nm peak is 38%).

Bearing in mind the dilution ratio (0.01, in our case), we obtain that the flotation coefficient for IgG aggregates in water Ka = I1(a)/I0 – 0.01 = 5%, where I0(a) and I1 are peak intensities at ∼ 300 nm in the distributions, as shown in Figure 8 (initial solution after shaking) and Figure 10 (100-fold diluted shaken solution). We can see that the flotation of monomeric IgGs is more efficient than that of their aggregates, which is obviously due to the lower volume number density of the aggregates.

2.4. Solution of IgG in an EWM: Characterization of IgG Aggregates

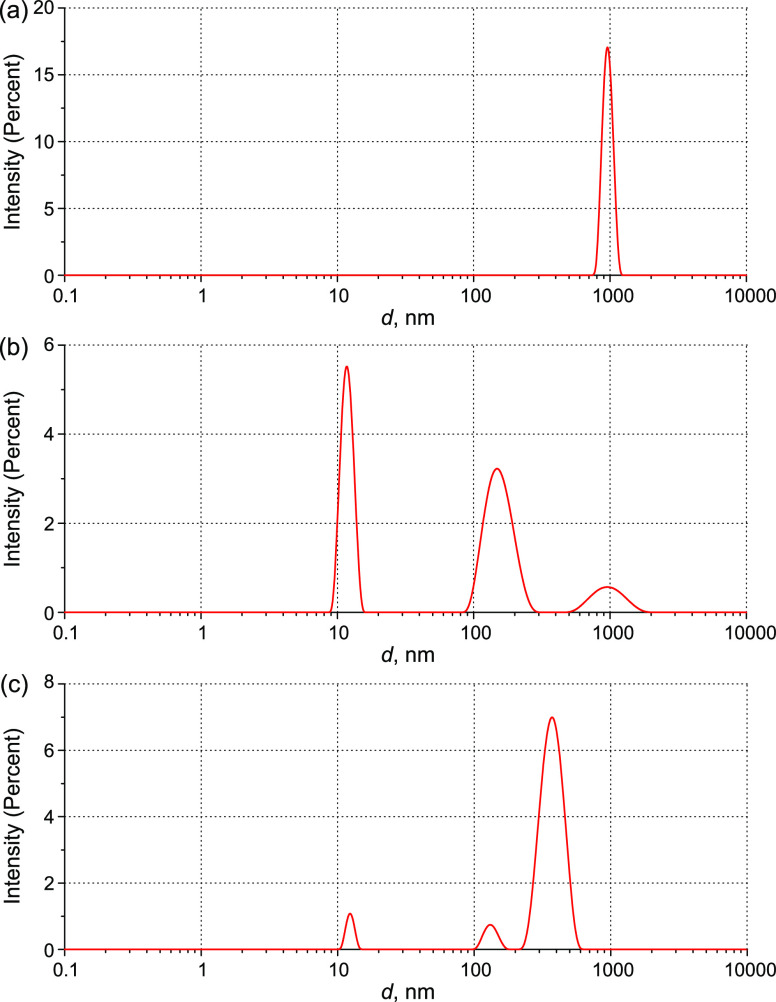
Figure 11 shows the results of DLS experiments with a solution of IgG in an EWM (the number of IgG molecules per unit volume is 3 × 1014 cm–3). As follows from Figure 11a, the aggregation of IgG monomers develops more intensively in an EWM than in water: in the scattered intensity distribution, we cannot see particles with a size of 12 nm, and the resultant aggregates are significantly larger than in those aqueous solutions; their size was about 900 nm (Figure 11a). To study smaller-sized fractions (of about 450 nm or less), the initial IgG solution was filtered through a membrane with a pore diameter of 450 nm (Figure 11b). As follows from the graph, a peak, centered at 900 nm, has the same physical nature as the corresponding peak in panel (a), but its intensity is significantly lower than that in the unfiltered sample. Apparently, this is due to the fast emergence of new aggregates after filtration. Because of the elimination of large particles and a decrease in the total scattering intensity by 116 times, individual molecules (12 nm) become visible. Furthermore, there can be seen a peak at ∼150 nm, which is characteristic for pure ethanol mesodroplets in an EWM,32,33 and a peak at d = 12 nm, corresponding to monomeric IgG molecules. To trace the behavior of monomer and aggregate peaks, we applied the shaking procedure (described in Section 5.1) to the filtered IgG solution (Figure 11b); the resulting distribution is shown in Figure 11c. At the first glance, it may seem strange that in an EWM, we see the same size of IgG molecules as in water, that is, the peak corresponding to IgG molecules in the native form (12 nm). Seemingly, the denatured protein molecules have enough time to assemble into aggregates; therefore, native IgG predominates in the peak of individual molecules.

Figure 11.

Figure 11

Open in a new tab

DLS intensity distribution over the particle sizes: (a) initial IgG solution in an EWM (36.7 vol %) with a volume number density of IgG molecules being 3 × 1014 cm–3, Itot(173°) = 5820 kcps before shaking; (b) same solution after filtration through a membrane with a pore size of 450 nm, Itot(173°) = 50 kcps (12 nm peak is 40%, 150 nm peak is 50%, and 900 nm peak is 10%); and (c) filtered solution immediately after shaking Itot = 389 kcps, 12 nm peak is 5%, 120 nm peak is 5.7%, and 400 nm peak is 89.3%). Here, Itot is the average total intensity (background scattering was subtracted).

The shaking process initiates the aggregation of IgG molecules so that the new aggregates about 400 nm in size appear and the total scattering intensity increases greatly (Figure 11c). As a result, larger aggregates ∼900 nm that existed in the solution before shaking in small quantities become invisible possibly because of their fragmentation. The aggregative nature of the 400 nm peak is confirmed by the fact that shaking of the pure (IgG-free) EWM (36.7 vol %) does not lead to any changes in the total scattering intensity and its scatterer size distribution (a peak corresponding to nanobubbles does not appear); the distribution in the EWM has only one peak in the 100 nm range related to ethanol mesodroplets.

Figure 12 shows the distribution corresponding to the solution in the EWM filtered through a porous membrane (pore diameter 0.45 μm), which was further filtered using a membrane with a pore size of 220 nm; the distribution peak corresponding to IgG aggregates completely disappeared. In this case, the peak corresponding to individual molecules is shifted to the right compared to Figure 11b in the position of 18 nm, which indicates an increase in the effective size of IgG molecules because of denaturation. An additional peak at a 4 Å scale (the characteristic size of an ethanol molecule) associated with molecular scattering is clearly observed. The effect of the IgG peak shift can be associated with a strong decrease in the concentration of IgG molecules, and because it is known that denatured protein molecules aggregate more efficiently than the native ones, at a lower concentration of IgG molecules, the IgG molecules in the denatured form do not have enough time to aggregate and we see an increase in the contribution of the denatured IgG molecules to the peak of the individual molecules, which causes the shift of this peak toward large sizes.

Figure 12.

Figure 12

Open in a new tab

DLS intensity distribution over the particle sizes in the initial IgG solution (3 × 1014 cm–3) after filtration through a membrane with a pore size of 220 nm, Itot(173°) = 27 kcps (4.5 nm peak is 22.8%, 18 nm peak is 31.4%, and 170 nm peak is 45.8%).

Figure 13 shows the LPM image of a particle, related to the 900 nm peak observed by DLS in EWM solution of IgG with volume number density α1 = 3 × 1014 cm–3 (see Figure 11a). The phase profile (Figure 13b) allows us to estimate the refractive index of such particles; we obtain n = 1.51 ± 0.02, which can be related to IgG aggregates, see the comments to Figure 5. Taking into account the measured average intensity I(173°) = 5400 kcps, we can estimate the volume number density α2 of 900 nm IgG aggregates through their scattering cross section Csca = 0.2943 μm2; F(173°) = 0.026, see the comments to eqs 4 and 5. Thus, we obtain α2 ≈ 1.7 × 108 cm–3.

Figure 13.

Figure 13

Open in a new tab

LPM images of a particle with a size of ≈900 nm in EWM solution of IgG before shaking: (a) 2D distribution of the OPD and (b) 1D profile of the distribution.

In Figure 14, we exhibit the experimental and theoretical angular dependences of the scattering matrix elements for the initial solutions of IgG in an EWM (3 × 1014 cm–3). Using the same algorithm for the analysis of matrix elements as for the aqueous IgG solution (Section 2.1), we estimated the fractal dimension of IgG aggregates in the EWM Df = 2.8.

Figure 14.

Figure 14

Open in a new tab

Dependences of the scattering matrix elements F11(θ), f12(θ), f34(θ), and f44(θ) measured via LPS in EWM solution of IgG before shaking. The circles are experimental points, the solid line is the theoretical approximation by multitype spherical particles, and the dotted line is the Rayleigh–Gans–Debye approximation for IgG aggregates. As in Figure 7, F11(exp) (θ) is plotted so that F11 (30°) = F11(theor) (30°).

2.5. IgG Flotation Efficiency with a Shaken EWM

To determine the flotation coefficient of single IgG macromolecules in an EWM, we use the size distribution of the solution filtered from aggregates, which manifests a 10 nm peak corresponding to IgG macromolecules, before (Figure 11b) and after shaking (Figure 11c). Furthermore, we measured the size distribution of 100-fold dilution of the initial IgG solution in the same EWM to determine the flotation coefficient for IgG aggregates (Figure 18).

Figure 18.

Figure 18

Open in a new tab

DLS intensity distribution over the particle sizes in monodisperse aqueous suspensions of polystyrene latex spheres at a scattering angle of 173°: (a) d = 200 nm and (b) d = 1200 nm.

Calculated similarly to what was described in Section 2.2, the flotation coefficients in the EWM have the following values. For single IgG molecules, we have Km = 3% (12–13 nm peak, as shown in Figure 11b,c); because for IgG aggregates, I1(a)/I0 = 2% (700–900 nm peak, as shown in Figures 11a and 15), we obtain Ka = I1(a)/I0 – 0.01 = 1% for aggregates. Thus, both Km and Ka in the EWM within the experimental error correspond to the usual 100-fold dilution, and the flotation effect does not manifest itself.

Figure 15.

Figure 15

Open in a new tab

DLS intensity distribution over the particle sizes for 100-fold dilution of shaken IgG solution in an EWM (the initial concentration 3 × 1014 cm–3). Average total intensity (minus background scattering) Itot(173°) = 157 kcps (150 nm peak is 20%, and 750 nm peak is 80%).

2.6. Visualization of Floating Bubbles and Flotation Foam with a Transmission Optical Microscope

We studied the flotation process induced by shaking with the aid of a transmission microscope DigiMicro 2.0 (depth of field d = 7 mm). Figure 16a presents an example of IgG aqueous solution with the concentration of IgG molecules 3 × 1012 cm–3. It is seen that flotation foam is formed at the interface; this foam consists of numerous millimeter-sized bubbles, resulted from coalescence of smaller bubbles (see the pattern under the foam, where the bubbles with radii 10 < R < 100 μm are visible). Millimeter-sized bubbles disappear within ∼30 s after shaking. In Figure 16b, we give a pattern, obtained with pure water; the sizes of floating bubbles are approximately the same both in water and in aqueous IgG solution. As follows from the microscope images, the volume number density of micrometer-sized bubbles (averaged over the volume V = dS, where S is the frame area) for pure water (Figure 16b) is αbub ≈ 200 cm–3. Obviously, in the presence of IgG aggregates, the αbub value is much larger because these aggregates serve as microbubble nucleation centers.

Figure 16.

Figure 16

Open in a new tab

Micrographs of gas bubbles in liquid samples, recorded immediately after shaking: (a) aqueous IgG solution with the concentration 3 × 1012 cm–3 and (b) pure water.

Figure 17a presents an image of water–ethanol IgG solution with a concentration of IgG molecules 3 × 1012 cm–3. It is seen that unlike the aqueous solution (cf. Figure 16a), in an EWM, flotation foam is practically absent. Figure 17b exhibits rising bubbles in a pure EWM, which is free of IgG particles. The radius of rising microbubbles lies in the range 30–200 μm, that is, they are larger than those in aqueous IgG solution. Note that in LPM experiments, carried out with IgG solution in an EWM, we did not see coarse particles, composed of gas bubbles and IgG aggregates, by contrast to aqueous IgG solution, see Figure 9. Thus, despite the visibility of rising bubbles, the flotation regime for IgG in an EWM essentially differs from that in aqueous solution.

Figure 17.

Figure 17

Open in a new tab

Micrographs of gas bubbles in the samples, recorded immediately after shaking: (a) solution of IgG in an EWM with the concentration 3 × 1012 cm–3 and (b) pure ethanol.

3. Conclusions

The study of shaking procedures has first shown that the aggregation of IgG molecules is enhanced. The aggregation proceeds more intensively in an EWM because of IgG denaturation as compared to water. Second, shaking induces flotation which is because of several complex factors. In aqueous solutions, there always exists an ion-stabilized nanobubble (bubston) phase: negative ions are adsorbed at the bubston interface, that is, its surface is electrically charged. As a consequence, foreign particles are attracted to the surface of bubstons because of the Coulomb monopole–dipole or positive–negative interaction; these particles can be monomeric IgG molecules, their aggregates, and also some solid impurity particles. However, bubstons have almost neutral buoyancy; therefore, the aggregates of bubstons with other particles cannot rise to the liquid surface. At the same time, macroscopically electroneutral micrbubbles with sizes of 10–100 μm are generated while shaking; these bubbles float to the surface because of Archimedean force. Microbubbles and nanobubbles attract suspended particles (IgG molecules and aggregates) with the formation of agglomerates that are transferred to the surface by larger bubbles (macrobubbles) because of nanobubble–macrobubble adhesion. Thus, bubstons serve as “spatial agents” (collectors) for flotation. At the same time, the content of ions in an EWM is essentially less compared to that in water, and this is why the ion-adsorption mechanism for the stabilization of nanobubbles probably does not act in an EWM, that is, the bubston phase cannot form. When shaking, macroscopic bubbles are also formed in an EWM, but these bubbles are almost electrically neutral, and therefore, Coulomb interaction between the bubbles and suspended particles is negligible. Meanwhile, there exists an alternative mechanism of adhesion to micro- and macrobubbles because of hydrophobic attraction; apparently, this mechanism should work equally in water and an EWM because it implies interaction of electrically neutral particles. This interaction is essentially short-range, and therefore, it can be ignored because of a relatively low concentration of floating bubbles (over ∼10 μm in size) obtained by shaking (∼103 cm–3 in water and even less in an EWM), while nanobubbles in water (whose concentration is high) cannot float up owing to their small size.

The considered flotation effect accompanying the shaking procedure leads to a significant discrepancy between the actual measured molecular concentrations and the dilution ratio, if an aliquot to be diluted is taken from the surface of the liquid. Taking into account the flotation effect, the maximum fraction of IgG macromolecules that can be transferred to a new liquid sample as a result of the dilution process with shaking is Km = 0.13. This efficiency is obviously limited by a small number of floating-up bubbles (∼103 cm–3) generated by the shaking procedure used by us per unit volume. In fact, the flotation coefficient could be much larger, reaching up to 100%, if shaking would generate so many floating-up bubbles that the distance between them would be comparable to their size. Thus, in multiple dilutions of IgG aqueous solution, the volume number density of IgG macromolecules decreases by at least the factor Kmn (n is the number of dilutions). If the flotation coefficient is assumed to be independent of the dilution number, for the initial volume number density of IgG macromolecules 3 × 1014 cm–3, we have the upper estimate (3 × 1014) × (0.13)n. For IgG aggregates, we obtained that a fraction of Ka = 0.05 is transferred into 100-fold dilution of shaken IgG aqueous solution, that is, the volume number density of IgG aggregates decreases with n-step dilution by at least the factor Kan = (0.05)n. Because the initial volume number density of IgG aggregates is 6 × 107 cm–3, it is clear that we cannot observe these aggregates for n > 4.

Summarizing, the calculation of the volume number density of particles in solutions of low and ultralow concentrations prepared using the technique of a multistage decrease in the concentration of a substance using shaking at each stage is not correct without considering the flotation effects. These effects may explain the results of studies proving the presence of nanoscale substances in solutions of ultralow concentrations, including those shown by us in the article.45

4. Materials

Affinity-purified rabbit immunoglobulin G (IgG) dispersions in water and water–ethanol mixtures were used as test liquid samples. The initial liquid samples were purchased from AB Biotechnology Limited (UK, Edinburgh). Nanofiltration was used to remove impurity particles and viruses; the initial suspensions were first diluted in glycine buffer (pH = 7.2) up to a weight concentration of 0.125 mg/mL (3 × 1014 cm–3) and then sterilized by filtration through 0.22 μm syringe filters (Sartorius, Germany). SDS-PAGE electrophoresis and high-performance liquid chromatography–size exclusion chromatography technique were used to assess identity and purity (≥95%) of the samples prepared. For producing diluted samples, we used purified water produced using Milli-Q Integral 5 (Merck Millipore, France) with pH = 5.5 (water samples were saturated with atmospheric gases and contained dissolved CO2) or an EWM with an ethanol content of 36.7 vol % (Sigma-Aldrich, USA) and pH = 6.0. From the literature, the IEP of rabbit IgG pH = 8.61.46

5. Experimental Section

5.1. Shaking and Dilution Procedures

Initial solutions of IgG in water and EWM were prepared in 20 mL borosilicate glass vials (Glastechnik Grafenroda, Germany) at room temperature without direct sunlight exposure by vortexing for 1 min at a frequency of 30 Hz and amplitude ∼1 mm to create a uniform distribution of particles throughout the volume using a Heidolph Multi Reax (545-10000-00) vortex mixer. For each measurement, an individual vial taken from a sterile factory packaging was used, and the pipettes were disposable. To study the disperse composition via DLS, 1.2 mL of the sample of each initial solution was poured into a 4.5 mL polystyrene square cuvette 10 × 10 × 45 mm (Sarstedt, Germany) for Malvern Zetasizer Nano use and hermetically sealed. Subsequently, the sample was shaken by oscillations in a vertical plane with an amplitude of 10 mm and a frequency of 5 Hz for 30 s to initiate the flotation process using an IKA orbital shaker, in which the platform was oriented vertically. It is important that shaking with such a large oscillation amplitude causes turbulent mixing of the solution with air from the free volume of the vial, resulting in the formation of a large amount of bubbles. To determine the number of protein particles carried to the surface of the sample because of shaking, we applied a 100-fold dilution procedure, which was as follows: 0.012 mL of the aliquot from the surface of the shaken solution and 1.188 mL of the diluent were mixed in one cuvette and then vortexed for homogenization.

5.2. Experimental Techniques

All samples were studied by three methods: DLS, LPM, and LPS. The DLS method allowed us to obtain the scattered light intensity distribution over the sizes of particles within the range of 1 to 105 nm from the time correlation function under the assumption that the particle shape is spherical. With the use of LPM, we can estimate the refractive index. LPM reliably determines the size of dispersed particles, whose size exceeds 100 nm. LPS measures the dependences of the scattering matrix on the scattering angle. DLS experiments were performed with a Zetasizer Nano ZS system (Malvern, UK) equipped with a continuous wave (CW) He–Ne laser at a wavelength of λ = 633 nm (maximum intensity 4 mW) and a temperature controller. Additionally, we used a Photocor-FC system (Photocor ltd, Russia) with second harmonic of CW YAG:Nd3+ laser (λ = 532 nm, maximum radiation power 40 mW) to verify the reproducibility of the peaks in size distributions of scattering intensity at different scattering angles and thus confirm their attribution to really existing particles and not to artifacts. The temperature of the samples was kept constant at 25 ± 0.5 °C. The autocorrelation function of scattering intensity was measured using a Zetasizer Nano ZS at an angle of 173° and using Photocor-FC at 30°.

For LPM, a semiconductor laser with a wavelength of λ = 405 nm was used. Drop samples of the studied liquids with a volume of 50 μL were placed on a mirror substrate, and then, a thin liquid layer formed from the spreading drop was examined by LPM. The phase microscope visualizes the spatial distribution of the phase shift between the interfering reference and object waves (for more detail, see ref (27)). In the presence of a particle in a liquid with a refractive index n, the phase shift changes by a value of

5.2. 1

Here, n0 is the refractive index of the liquid and d is the particle size. If n > n0, then the profile of δ is a convex function across the particle and in the opposite case, it is a concave one. This allows the determination of the size and shape of inhomogeneities. In an LPS setup, the measurable scattering angles fall in the range of 0–160°. We do not provide a detailed description of the setup here; this is given in ref (30).

5.3. Instrumental Calibration

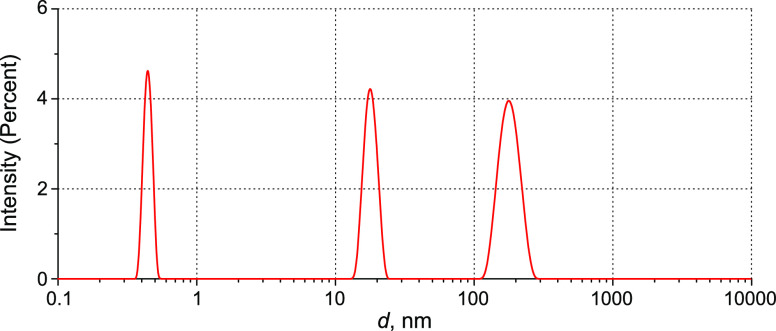
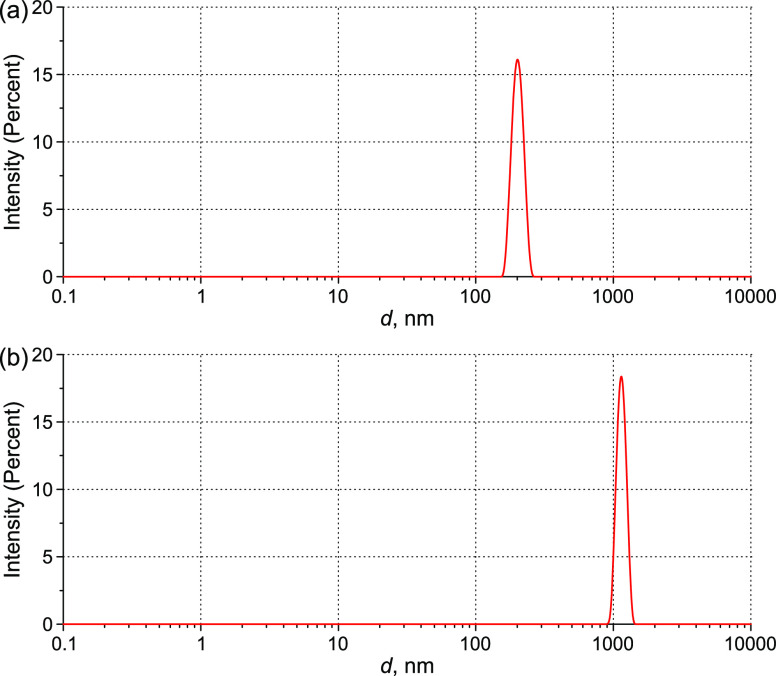
The DLS and LPM instruments were calibrated using monodisperse aqueous suspensions of polystyrene latex spheres (Sigma-Aldrich, USA) with average diameters d = 200 and 1200 nm and the refractive indices n = 1.59 and 1.62 for the wavelengths λ = 633 and 405 nm, respectively. Figure 18 shows the scattering intensity distribution over sizes of latex spheres in DLS experiments, which is normalized to the area under the curve.

The LPM technique allows us to determine the phase shift profiles between the object and reference waves interfering after the passage of the object wave through a particle in the liquid sample. The value of δ is conventionally measured in λ/2 units, that is, in nanometers, see eq 1. Thus, the value actually measured in LPM is the OPD Δh, which for a spherical particle is expressed as27,33

5.3. 2

Here, we introduced an apparatus coefficient γ, accounting for the diffraction distortion when measuring the spatial distribution of OPD on a submicron particle, in the geometric optics approximation γ = 2. The aim of calibration experiments was to determine the dependence of γ on the particle size in the 100–1000 nm size range. OPD measurements for latex particles are shown in Figure 19. The particle diameter is defined as the half-height of the OPD profile.

Figure 19.

Figure 19

Open in a new tab

LPM images (2D distribution of OPD and the corresponding 1D profiles) of spherical polystyrene latex particles in monodisperse aqueous suspensions: (a,b) particle with d = 200 nm and (c,d) particle with d = 1200 nm.

As seen in Figure 19b, the particle size measured by LPM is ∼1.3 times larger than the size measured by DLS, see Figure 18a. This is explained by diffraction blurring for the particle sizes ∼λ/2. Bearing in mind the refractive index of polystyrene n = 1.62 (λ = 405 nm), we obtain γ = 1.7 for 200 nm particles. For 1200 nm particles, we have γ = 2.7; the particle profile has a plateau segment. Such a behavior is because the size of the particle exceeds the objective field depth (0.73 μm). The calibration curve is shown in Figure 20; the error bars display random scatter caused by interference noise and inaccurate focusing. This dependence was used to determine the refractive index of particles according to eq 2.

Figure 20.

Figure 20

Open in a new tab

Dependence of the coefficient γ vs particle size.

The LPS setup was calibrated with the same latex solutions. For the sake of brevity, we do not present the calibration graphs for the scattering matrix elements here, but only note that because of the influence of stray reflections and scattering, the reliable scattering matrix measurements were restricted to the angles 0–90°.

6. Computational Methods

6.1. Calculation of Scatterer Number Density

Below, we derive formulas for estimating the number of particles per unit volume of a liquid dispersion from scattering coefficient measurements. The scattering coefficient R(θ) (also called “the Rayleigh ratio”) is defined through the scattering intensity I(θ) as

6.1. 3

where I0 is the intensity of the incident light, V is the scattering volume, and L is the distance from the center of the scattering volume to the observation point. Thus, the integral scattering coefficient is

6.1. 4

where Ω is the solid angle, α = N/V is the volume number density of scatterers, and Csca is the scattering cross section of a single particle. We define the scattering indicatrix of a single particle as F(θ) = I1(θ)/I0, where I1(θ) is the scattering intensity of a single particle and the relationship Inline graphic should be met. Thus, we arrive at

6.1. 5

Following common practice, we use toluene (with known scattering coefficient) for calibration. The relationship between the scattering coefficients of the sample under study and toluene (R(θ) and RTol(θ)) is given as47

6.1. 6

Here, I(θ) is the scattering intensity of the sample under study and ITol(θ) is the scattering intensity of toluene. Here, nsolv is the refractive index of the diluent, where the particles are suspended, and nTol is the refractive index of toluene. Finally, we refine the value of the volume number density of particles using the average scattering intensity at a fixed scattering angle and the total scattering cross section of a single particle

6.1. 7

where ITol(173°) = 105 kcps, RTol(173°) = 22 × 10–6 cm–1, and nTol(λ = 0.633 μm) = 1.49.

Values of Csca and scattering indicatrix F(θ) were calculated using the program code developed by Mishchenko for spherical particles.40

6.2. Theoretical Approximation of Scattering Matrices for IgG Dispersions

An approximate structural model of IgG dispersions constructed on the basis of DLS and LPM data, that is, the number of different types of particles found and the measured values of their sizes and refractive indices are used as a priori information to solve the inverse problem for the scattering matrix measured by LPS. Ultimately, the solution of such an inverse problem refines and supplements the structural model.

To confirm the aggregative nature of the submicron particles observed in IgG dispersions, we theoretically modeled the scattering matrix for a system containing IgG aggregates, considered as fractal clusters of IgG macromolecules. The theoretical scattering matrices of IgG dispersions were approximated by a weighted sum of matrices Fij(p) (θ) calculated for a model of spherical particles of several types: monomeric particles with the diameter d = 12 nm, bubstons with d = 250 nm, and IgG aggregates with the average diameter ⟨d⟩ = 350 nm and the distribution width 200–500 nm, as follows

6.2. 8

where p is the type of particles, αp stands for the volume number density of particles of the corresponding type (e.g., for IgG monomers and aggregates, αp = 2.5 × 1014 cm–3 and 5.4 × 107 cm–3, while for bubstons in water, αp ≈ 106 cm–3, see ref (26)), Cpsca is the scattering cross section, and Fij(p) are the matrix elements of the pth type of particles. The total number of the types of model particles is 14; 12 of them are related to aggregates with gyration radii 100–2000 nm. While calculating eq 9, we assume that the values of F12(θ), F34(θ), and F44(θ) for the monomers coincide with the corresponding elements of the Rayleigh scattering matrix (dashed curves) because the monomers in aggregates are much smaller than those in the radiation wavelength. The values of the element F11(θ) and the scattering cross sections for the IgG aggregates were calculated in the Rayleigh–Hans–Debye approximation. If the condition qRg > 1 is met for a cluster, F11 is described by

6.2. 9

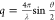where Inline graphic is the modulus of the scattering vector, Df is the fractal dimension of the cluster, and Rg is the gyration radius of the cluster.41

Acknowledgments

This work was supported by the research project “Physical Methods in Agriculture and Ecology” and the MEPhI Academic Excellence Project, contract no. 02.a03.21.0005. Part of the work related to studying the properties of protein aggregates was supported by the Russian Foundation for Basic Research (20-34-70037). Part of the work related to the methods for characterization of nano-objects was supported by the grant from the Presidential Council for state support of young Russian scientists (MD-2128.2020.11). The authors are grateful to the Center for Collective Use of GPI RAS for the equipment provided.

The authors declare no competing financial interest.

References

  1. Gudkov S. V.; Lyakhov G. A.; Pustovoy V. I.; Shcherbakov I. A. Influence of Mechanical Effects on the Hydrogen Peroxide Concentration in Aqueous Solutions. Phys. Wave Phenom. 2019, 27, 141–144. 10.3103/s1541308x19020092. [DOI] [Google Scholar]
  2. Lee J. K.; Walker K. L.; Han H. S.; Kang J.; Prinz F. B.; Waymouth R. M.; Nam H. G.; Zare R. N. Spontaneous generation of hydrogen peroxide from aqueous microdroplets. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 19294–19298. 10.1073/pnas.1911883116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Rieth M.; Kempf A. M.; Stein O. T.; Kronenburg A.; Hasse C.; Vascellari M. Evaluation of a flamelet/progress variable approach for pulverized coal combustion in a turbulent mixing layer. Proceedings of the Combustion Institute 2019, 37, 2927–2934. 10.1016/j.proci.2018.05.150. [DOI] [Google Scholar]
  4. Nada M. H.; Gillan E. G.; Larsen S. C. Mechanochemical reaction pathways in solvent-free synthesis of ZSM-5. Microporous Mesoporous Mater. 2019, 276, 23–28. 10.1016/j.micromeso.2018.09.009. [DOI] [Google Scholar]
  5. Belhouchet H.; Sahraoui T.; Belhouchet K.; Romero M. Influence of heating rate and mechanical activation on the reaction between kaolin and aluminium powder. J. Aust. Ceram. Soc. 2019, 55, 135–144. 10.1007/s41779-018-0219-y. [DOI] [Google Scholar]
  6. European Directorate for the Quality of Medicines & HealthCare . European Pharmacopoeia, 9th Edition, Suppl. 9.3; Council of Europe: Strasbourg, 2017. [Google Scholar]
  7. Banga A. K.Therapeutic Peptides and IgGs: Formulation, Processing, and Delivery Systems; CRC Press: Boca Raton, 2015. [Google Scholar]
  8. Wang W.; Roberts C. J.. Aggregation of therapeutic IgGs; John Wiley & Sons, Inc.: Hoboken, New Jersey, 2010. [Google Scholar]
  9. Joubert M. K.; Luo Q.; Nashed-Samuel Y.; Wypych J.; Narhi L. O. Classification and Characterization of Therapeutic Antibody Aggregates. J. Biol. Chem. 2011, 286, 25118. 10.1074/jbc.m110.160457. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Evdokimov I. A.; Titov S. A.; Titov S. A.; Polyansky K. K.; Saiko D. S. Ultrafiltration concentrating of curd whey after electroflotation treatment. Foods Raw Mater. 2017, 5, 131–136. 10.21179/2308-4057-2017-1-131-136. [DOI] [Google Scholar]
  11. Yoon R.-H. The role of hydrodynamic and surface forces in bubble–particle interaction. Int. J. Min. Process 2000, 58, 128–143. 10.1016/s0301-7516(99)00071-x. [DOI] [Google Scholar]
  12. Ralston J.; Fornasiero D.; Hayes R. Bubble–particle attachment and detachmentin flotation. Int. J. Min. Process 1999, 56, 133–164. 10.1016/s0301-7516(98)00046-5. [DOI] [Google Scholar]
  13. Rubio J.; Capponi F.; Matiolo E.; Nunes D.; Guerrero C. P.; Berkowitz G.. Advances in flotation of mineral fines. Proceedings XXII International Mineral Processing Congress (IMPC), 2003; pp 1014–1022.
  14. Fuerstenau M. C.; Yoon R. H.; Jameson G. J.. Froth Flotation: A Century of Innovation; Society for Mining, Metallurgy, and Exploration, 2007. [Google Scholar]
  15. Sobhy A.; Tao D. Nanobubble column flotation of fine coal particles and associated fundamentals. Int. J. Min. Process. 2013, 124, 109–116. 10.1016/j.minpro.2013.04.016. [DOI] [Google Scholar]
  16. Ahmadi R.; Khodadadi D. A.; Abdollahy M.; Fan M. Nano-microbubble flotation of fine and ultrafine chalcopyrite particles. Int. J. Min. Sci. Technol. 2014, 24, 559–566. 10.1016/j.ijmst.2014.05.021. [DOI] [Google Scholar]
  17. Calgaroto S.; Azevedo A.; Rubio J. Flotation of quartz particles assisted by nanobubbles. Int. J. Min. Process. 2015, 137, 64–70. 10.1016/j.minpro.2015.02.010. [DOI] [Google Scholar]
  18. Azevedo A.; Etchepare R.; Calgaroto S.; Rubio J. Aqueous dispersions of nanobubbles: generation, properties and features. Miner. Eng. 2016, 94, 29–37. 10.1016/j.mineng.2016.05.001. [DOI] [Google Scholar]
  19. Etchepare R.; Oliveira H.; Nicknig M.; Azevedo A.; Rubio J. Nanobubbles: Generation using a multiphase pump, properties and features in flotation. Miner. Eng. 2017, 112, 19–26. 10.1016/j.mineng.2017.06.020. [DOI] [Google Scholar]
  20. Rosa A. F.; Rubio J. On the role of nanobubbles in particle–bubble adhesion for the flotation of quartz and apatitic minerals. Miner. Eng. 2018, 127, 178–184. 10.1016/j.mineng.2018.08.020. [DOI] [Google Scholar]
  21. Craig V. S. J.; Ninham B. W.; Pashley R. M. Effect of Electrolytes on bubble coalescence. Nature 1993, 364, 317–319. 10.1038/364317a0. [DOI] [Google Scholar]
  22. Craig V. S. J.; Ninham B. W.; Pashley R. M. The Effect of Electrolytes on Bubble Coalescence in Water. J. Phys. Chem. 1993, 97, 10192–10197. 10.1021/j100141a047. [DOI] [Google Scholar]
  23. Henry C. L.; Craig V. S. J. Inhibition of Bubble Coalescence by Osmolytes: Sucrose, Other Sugars, and Urea. Langmuir 2009, 25, 11406–11412. 10.1021/la9015355. [DOI] [PubMed] [Google Scholar]
  24. Horn R. G.; Ninham B. W.. Experimental studies of solvation forces in Micellar Solutions and Microemulsions. In Micellar Solutions and Microemulsions; Chen S. H., Rajagopalan A., Eds.; Springer-Verlag: New York; Chapter 5, 1990. [Google Scholar]
  25. Pashley R. M.; Ninham B. W. Double-layer forces in ionic micellar solutions. J. Phys. Chem. 1987, 91, 2902–2904. 10.1021/j100295a049. [DOI] [Google Scholar]
  26. Fang Z.; Wang X.; Zhou L.; Zhang L.; Hu J. Formation and Stability of Bulk Nanobubbles by Vibration. Langmuir 2020, 36, 2264–2270. 10.1021/acs.langmuir.0c00036. [DOI] [PubMed] [Google Scholar]
  27. Bunkin N. F.; Shkirin A. V.; Suyazov N. V.; Babenko V. A.; Sychev A. A.; Penkov N. V.; Belosludtsev K. N.; Gudkov S. V. Formation and Dynamics of Ion-Stabilized Gas Nanobubble Phase in the Bulk of Aqueous NaCl Solutions. J. Phys. Chem. B 2016, 120, 1291–1303. 10.1021/acs.jpcb.5b11103. [DOI] [PubMed] [Google Scholar]
  28. Yurchenko S. O.; Shkirin A. V.; Ninham B. W.; Sychev A. A.; Babenko V. A.; Penkov N. V.; Kryuchkov N. P.; Bunkin N. F. Ion-Specific and Thermal Effectsin the Stabilization of the Gas NanobubblePhase in Bulk Aqueous Electrolyte Solutions. Langmuir 2016, 32, 11245–11255. 10.1021/acs.langmuir.6b01644. [DOI] [PubMed] [Google Scholar]
  29. Bunkin N. F.; Ninham B. W.; Ignatiev P. S.; Kozlov V. A.; Shkirin A. V.; Starosvetskij A. V. Long-living nanobubbles of dissolved gas in aqueous solutions of salts and erythrocyte suspensions. J. Biophotonics 2011, 4, 150–164. 10.1002/jbio.201000093. [DOI] [PubMed] [Google Scholar]
  30. Bunkin N. F.; Shkirin A. V.; Kozlov V. A.; Starosvetskiy A. V.. Laser scattering in water and aqueous solutions of salts. Laser Applications in Life Sciences, 2010; Vol. 7376, p 73761D.
  31. Marâechal Y.The Hydrogen Bond and the Water Molecule, The Physics and Chemistry of Water, Aqueous and Bio Media; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
  32. Bunkin N. F.; Shkirin A. V.; Lyakhov G. A.; Kobelev A. V.; Penkov N. V.; Ugraitskaya S. V.; Fesenko E. E. Jr. Droplet-like heterogeneity of aqueous tetrahydrofuran solutions at the submicrometer scale. J. Chem. Phys. 2016, 145, 184501. 10.1063/1.4966187. [DOI] [PubMed] [Google Scholar]
  33. Bunkin N. F.; Lyakhov G. A.; Shkirin A. V.; Krivokhizha S. V.; Afonin A. A.; Kobelev A. V.; Penkov N. V.; Fesenko E. E. Jr. Laser Diagnostics of the Mesoscale Heterogeneity of Aqueous Solutions of Polar Organic Compounds. Phys. Wave Phen. 2018, 26, 21–35. 10.3103/s1541308x18010041. [DOI] [Google Scholar]
  34. Françon M.La granularite laser (spekle) et ses applications en optique; Masson: Paris, New York, 1978. [Google Scholar]
  35. Jadhav A. J.; Barigou M. Bulk Nanobubbles or Not Nanobubbles: That is the Question. Langmuir 2020, 36, 1699–1708. 10.1021/acs.langmuir.9b03532. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Malyuchenko N. V.; Tonevitskii A. G.; Savvateev M. N.; Bykov V. A.; Moisenovich M. M.; Agapov I. I.; Kozlovskaya N. V.; Arkhipova V. S.; Yegorova S. G.; Kirpichnikov M. P. Study of the structural features of proteins by intermittent-contact atomic force microscopy. Biophysics 2003, 48, 772–778. [PubMed] [Google Scholar]
  37. Subramanian D.; Boughter C. T.; Klauda J. B.; Hammouda B.; Anisimov M. A. Mesoscale Inhomogeneities in Aqueous Solutions of Small Amphiphilic Molecules. Faraday Discuss. 2013, 167, 217–238. 10.1039/c3fd00070b. [DOI] [PubMed] [Google Scholar]
  38. Hand D. B. The refractivity of protein solutions. J. Biol. Chem. 1935, 108, 703–707. [Google Scholar]
  39. Kimura H. Light-scattering properties of fractal aggregates: numerical calculations by a superposition technique and the discrete-dipole approximation. J. Quant. Spectrosc. Radiat. Transfer 2001, 70, 581–594. 10.1016/s0022-4073(01)00031-0. [DOI] [Google Scholar]
  40. Mishchenko M. I.; Travis L. D.; Lacis A. A.. Scattering, Absorption, and Emission of Light by Small Particles; Cambridge University Press: Cambridge, 2002. [Google Scholar]
  41. Feder J.Fractals; Springer: New York, 1988. [Google Scholar]
  42. Tazaki R.; Tanaka H.; Okuzumi S.; Kataoka A.; Nomura H. Light scattering by fractal dust aggregates. I. Angular dependence of scattering. Astrophys. J. 2016, 823, 70. 10.3847/0004-637x/823/2/70. [DOI] [Google Scholar]
  43. Cumper C. W. N. The stabilization of foams by proteins. Trans. Faraday Soc. 1953, 49, 1360–1369. 10.1039/tf9534901360. [DOI] [Google Scholar]
  44. Saint-Jalmes A.; Peugeot M.-L.; Ferraz H.; Langevin D. Differences between protein and surfactant foams: Microscopic properties, stability and coarsening. Colloids Surf., A 2005, 263, 219–225. 10.1016/j.colsurfa.2005.02.002. [DOI] [Google Scholar]
  45. Bunkin N. F.; Shkirin A. V.; Penkov N. V.; Chirikov S. N.; Ignatiev P. S.; Kozlov V. A. The Physical Nature of Mesoscopic Inhomogeneities in Highly Diluted Aqueous Suspensions of Protein Particles. Phys. Wave Phenom. 2019, 27, 102–112. 10.3103/s1541308x19020043. [DOI] [Google Scholar]
  46. Roitt I.Essential Immunology; Blackwell Scientific Publications: Oxford, 1994. [Google Scholar]
  47. Zetasizer Nano Series. User Manual. MAN0317 Issue 3.1 July 2007, Chapter 6. Sample Preparation; Malvern Instruments Ltd.: United Kingdom, 2007.

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES