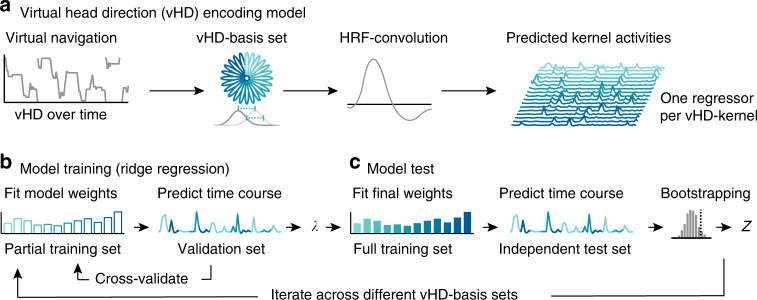
Fig. 2. Analysis logic.

a Virtual head direction (vHD) encoding model. We modeled vHD using multiple basis sets of circular–Gaussian kernels covering the full 360°. Given the observed vHD, we generated predicted time courses (regressors) for all kernels in each basis set. The basis sets differed in the (full-width-at-half-maximum) kernel width and number. Spacing and width were always matched to avoid overrepresenting certain directions, i.e., the broader each individual kernel, the fewer kernels were used. The resulting regressors were convolved with the hemodynamic response function (SPM12) to link the kernel activity over time to the fMRI signal. b Model training. We estimated voxel-wise weights for each regressor in a training data set (80% of all data of a participant or four runs, 10 min each) using ridge regression. To estimate the L2-regularization parameter (λ), we again split the training set into partial training (60% data, three runs) and validation sets (20% data, one run). Weights were estimated in the partial training set, and then used to predict the time course of the validation set via Pearson correlation. This was repeated for ten values of λ (log-spaced between 1 and 10.000.000) and cross-validated such that each training partition served as validation set once. We then used the λ that resulted in the highest average Pearson’s R to fit the final model weights using the full training set. c Model test: we used the final model weights to predict each voxel’s time course in an independent test set (held-out 20% data, always the run halfway through the experiment) via Pearson correlation. These Pearson correlations were used to test model performance on a voxel-by-voxel level (Figs. 3 and 4). For a region-of-interest analysis (Figs. 5 and 6), we additionally converted model performance into Z scores via bootstrapping, ensuring that the results reflected the effects of kernel width and not of number. The null distribution of each voxel was obtained by weight shuffling (k = 500). Both model training and test were repeated for all basis sets.