Improved Modeling of Cation-π and Anion-Ring Interactions Using the Drude Polarizable Empirical Force Field for Proteins

Abstract

Cation-π interactions are noncovalent interactions between a π-electron system and a positively charged ion that are regarded as a strong noncovalent interaction and are ubiquitous in biological systems. Similarly, though less studied, anion-π interactions are present in proteins along with in-plane interactions of anions with aromatic rings. As these interactions are between a polarizing ion and a polarizable π system, the accuracy of the treatment of these interactions in molecular dynamics (MD) simulations using additive force fields may be limited. In the present work, to allow for a better description of ion-π interactions in proteins in the Drude-2013 protein polarizable force field, we systematically optimized the parameters for these interactions targeting model compound quantum mechanical (QM) interaction energies with atom pair-specific Lennard-Jones parameters along with virtual particles as selected ring centroids introduced to target the QM interaction energies and geometries. Subsequently, MD simulations were performed on a series of protein structures where ion-π pairs occur to evaluate the optimized parameters in the context of the Drude-2013 FF. The resulting FF leads to a significant improvement in reproducing the ion-π pair distances observed in experimental protein structures, as well as a smaller root-mean-square differences and fluctuations of the overall protein structures from experimental structures. Accordingly, the optimized Drude-2013 protein polarizable FF is suggested for use in MD simulations of proteins where anion- and cation-π interactions are critical.

Introduction

Cation-π interactions are noncovalent interactions between a π-electron system and a positively charged ion or moiety. These interactions are typically regarded as strong, favorable noncovalent interactions.¹ Over the past decades, cation-π interactions have been extensively studied in proteins,¹ protein-DNA,^{2, 3} protein-lipid, and protein-ligand complexes,^{4, 5} including ion channels,^{6, 7} where they were found to play important roles in structural stability,⁸ catalysis⁹, molecular recognition,^{10, 11} and ion selectivity.^{6, 7} Within proteins, cation-π interactions can form between the positively charged side chains of lysine (Lys), arginine (Arg), or protonated histidine (His⁺) as well as the N teminus and the aromatic side chains of phenylalanine (Phe), tyrosine (Tyr), tryptophan (Trp) or neutral histidine (His),¹² such that cation-π interactions have been suggested to contribute to the stabilization of protein secondary^{8, 13} and tertiary structures.¹⁴

On the other hand, the aromatic systems have also been demonstrated to interact favorably with anions, termed anion-π interactions.^15–18 Several theoretical calculations have shown that the anion-π interactions could be dominated by electrostatic or anion-induced polarization contributions, depending on the magnitude of the quadrupole moment or molecular polarizability of the aromatic compound.^{17, 19, 20} Experimentally, the anion-π interactions were also observed in proteins or ligand-protein systems.^21–23 Surveys of anion-π interactions in Protein Data Bank have been performed as well, further quantitatively addressing the importance of these interactions in biological macromolecules, such as proteins, DNAs, and RNAs.^24–27

Molecular dynamics (MD) simulation-based methods are often used to model biological systems. To assure the accuracy of MD simulations, well-optimized force fields are required.²⁸ The most commonly used force fields are referred to as the additive force field (FF). Nowadays, a number of FFs for macromolecules, such as the AMBER,^29–31 OPLS,^{32, 33} GROMOS,^34–36 and CHARMM^37–42 FFs, among others, have been developed. However, the additive FFs have limitation in describing the polarization response as this property is treated in a mean-field fashion. Particularly with respect to ion-π interactions, which result from the attraction of a cation or anion and the polarizable π-electron cloud of an aromatic ring, the additive FF could poorly represent their interaction as their accurate reproduction requires the explicit treatment of induced polarization.^43–46 While careful parametrization of an additive FF resulted in better reproduction of the tyrosine-choline interactions,⁴⁷ studies have shown that the polarization effect could be critical in describing the cation-π interactions, such that the polarizable model could result in an improved modeling of the cation-π interactions.^48–50 Advances in the polarizable models have demonstrated the benefits of explicitly treating polarization, yielding improvements over the additive FFs in a range of system.^51–58 Recently, to lead to a more accurate representation of cation-π interactions improvements have been made in the polarizable AMOEBA^{59, 60} and the Drude polarizable FFs.^{48, 61}

The Drude polarizable FF has been successfully used to describe water,^{62, 63} a range of small molecules,^{64, 65, 65–68} proteins,⁶⁹ nucleic acids^70–72 and selected lipids.^{73, 74} The polarizability is treated via the classical Drude oscillator model,⁷⁵ where the electronic polarizability is introduced by using a charge-carrying auxiliary Drude oscillator (or particle) linked to each non-hydrogen atom via a harmonic bond.⁷⁵ Detailed description of the Drude polarizable model has been presented elsewhere.^{51, 56} Recently, Orabi et al optimized the cation-π interactions with the Drude polarizable model to recover consistent binding affinities for various cation-π pairs, though the improvements were limited to the aromatic side chains with ammonium moieties⁷⁶ and the atomic cations Li⁺, Na⁺ and K⁺.⁶¹ Similarly, Khan et al focused on the parametrization between tyrosine amino acids and compounds containing a N,N,N-trimethylethanolammonium.⁴⁸

In this work, we systematically optimized the Drude-2013 polarizable protein force field to better reproduce the cation-π interactions among protein side chains, including Lys, Arg, Phe, Tyr, Trp and His amino acids as well as the N terminus. The optimization was performed based on model compounds representative of protein positively charged and aromatic side chains. To improve these cation-π interactions, we introduced atom pair-specific LJ parameters⁷⁷ (NBFIX term in CHARMM) between the positively charged moieties and aromatic group heavy atoms as well as the addition of a virtual particle located at the center of the rings. These NBFIX parameters were optimized to reproduce the QM target data. Additionally, to ensure the anion-π interactions between the negatively charged side chains and C terminus and aromatic groups are accurately modelled, NBFIX parameters between the acetate and aromatic model compounds were introduced as well. Subsequently, the optimized FF was used in MD simulations on a series of protein structures to evaluate its ability to reproduce the cation- and anion-π interaction geometries observed in selected X-ray crystal and NMR structures. With these atom pair-specific parameters, the interaction distances between the cation- and anion-π pairs from the MD simulated structures were significantly improved compared with the original 2013 Drude polarizable protein FF. In addition, the overall root-mean-square differences and fluctuations of the proteins were decreased indicating the importance of the proper treatment of these interactions to protein structures. These results indicate that the Drude polarizable protein FF with optimized atom pair-specific LJ parameters can accurately treat the cation- and anion-π interactions, thereby indicating its utility in the simulations of proteins.

Computational Methods

Ab Initio Calculations

The quantum mechanical (QM) target data were prepared in using two approaches. The first approach is to calculate the single-point interaction energies based on rigid scanning of two gas-phase optimized molecules as a function of distance in different interaction orientations. The gas-phase QM geometry optimizations were performed at the MP2 level of theory with the aug-cc-pVDZ basis set⁷⁸ for the model compounds (Figure 1). These model compounds include benzene (BENZ), toluene (TOLU), phenol (PHEN), 4-methylphenol (CRES), indole (INDO), and 3-methylindole (MIND), imidazole (IMIM), 4-methylimidazole tautomers (4MIM and 4MIE) that represent the aromatic functional group of the amino acids, methylammonium (MAMM), methylguanidinium (MGUAN) and imidazolium (IMIM) that represent the positively charged side chains and the N terminus, and acetate (ACET) that represents the negatively charged side chains and C terminus. All the QM geometry optimizations and rigid scans were performed using Gaussian03.⁷⁹ The rigid scans were performed using the MP2/ aug-cc-pVDZ optimized monomer geometries by varying the distance between the two interacting model compounds from 1.5 to 5.0 Å in intervals of 0.1 Å. Single-point interaction energies were obtained at each distance with the RIMP2 level of theory with the cc-pVQZ basis set⁷⁸ and with the SAPT2+/aug-cc-pVDZ model chemistry⁸³ using PSI4.⁸⁰ The basis set superposition error (BSSE) in the RIMP2/cc-pVQZ calculations was corrected using the counterpoise method.⁸¹

Figure 1.

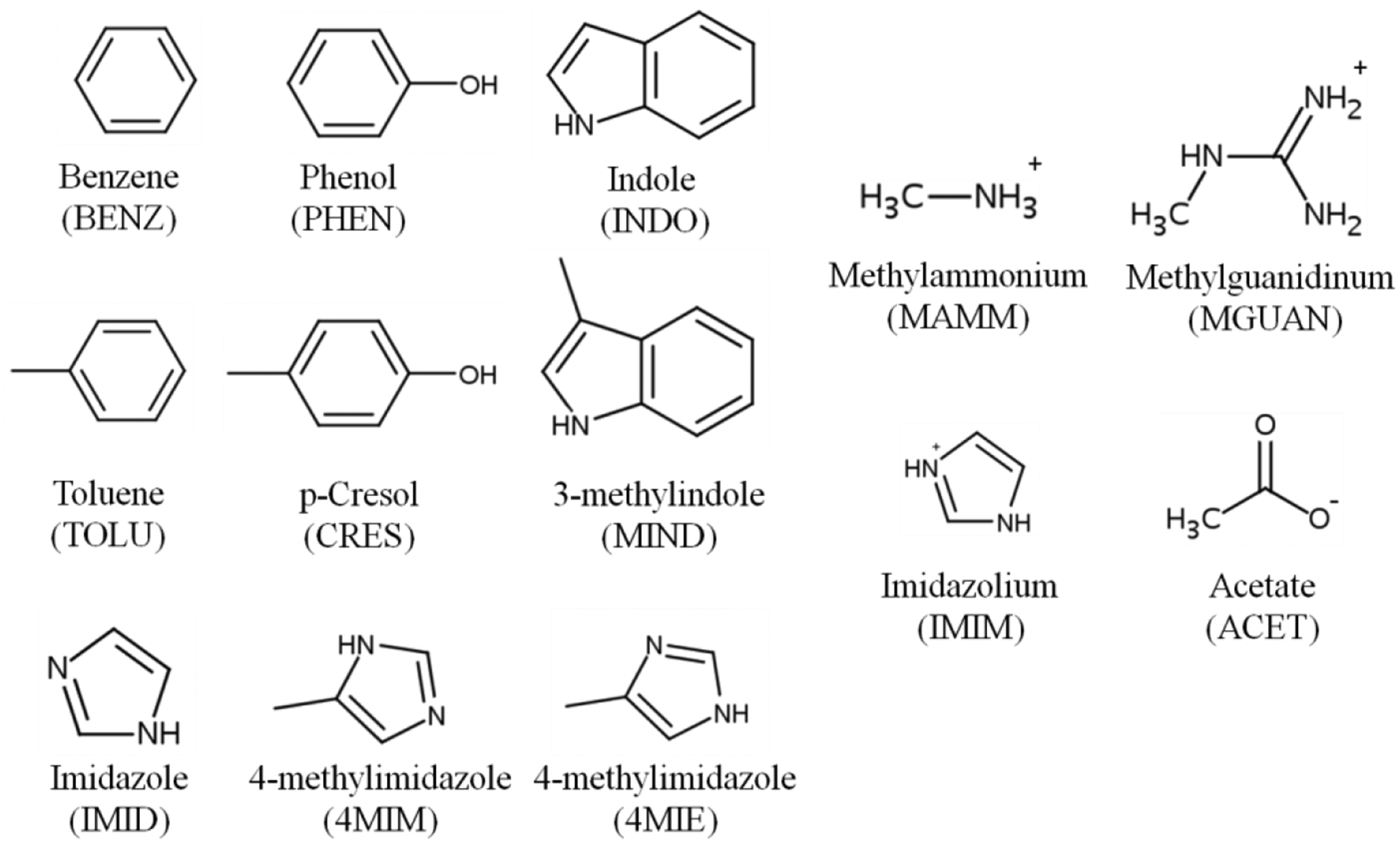
Abbreviations and 2D structures of the protein aromatic and charged model compounds.

In the second approach, fully optimized structures of each complex were calculated followed by single-point interaction energies. Each geometry obtained from the RIMP2/cc-pVQZ rigid scan at which the interaction energy was minimal was fully optimized at MP2/6–311++G(d,p) level⁸² using PSI4.⁸⁰ These optimized complexes were subsequently used to calculate single point energies at the RIMP2 level of theory with the cc-pVQZ basis set⁷⁸ including BSSE correction⁸¹ using PSI4⁸⁰ as well as with the SAPT2+/aug-cc-pVDZ model chemistry.⁸³

Molecular Mechanics Calculations.

Molecular mechanics (MM) minimum interaction energies and distances were determined using the QM gas phase optimized monomer structures from rigid scans with only the distance of interest varied, analogous to the first approach used in the QM calculations. As previously presented⁸⁴ and in analogy to the QM calculations, the interactions energies are based on the total energy of the dimer minus the energy of the monomers following optimization of the Drude particle positions with the real atoms fixed. The minimization, which satisfies the Born-Oppenheimer approximation, was performed using the steepest-descent (SD) algorithm with a step size of 0.01 to a force gradient of 10^–2 kcal·mol^–1·Å^–1 followed by the adopted basis Newton–Raphson algorithm (ABNR) with a step size of 0.02 to a force gradient of 10^–5 kcal·mol^–1·Å^–1 to relax the Drude particles while constraining all real atoms (e.g., applying the “CONS FIX” command in CHARMM^85–87) following which the constraints were removed and the energies calculated. In the case of the approach 2 fully optimized dimer structures, the Drude optimizations were initiated from the QM optimized structures. Minimizations involved relaxation of the Drude particles using the above protocol followed by a 100 step SD minimization to a force gradient of 10^–5 kcal mol^–1 Å^–1 and a 200 step ABNR minimization to a force gradient of 10^–5 kcal mol^–1 Å^–1. All non-bond interactions were included.

To improve the reproduction of the QM interactions by the MM model, virtual particles were introduced into the centroid of selected rings using the Lone Pair facility available in CHARMM^85–87 and other simulation packages. The center of the rings was defined along the bisector of the three atoms connected to the CB carbon (e.g. CG, CD1 and CD2 in Phe or Tyr) at a distance from the central atom that corresponds to the center of the ring in the MP2/aug-cc-pVDZ model compound optimized structure (Table S6 of supporting information). This definition was applied to maintain compatibility with the programs NAMD^{88, 89} and OpenMM.^{90, 91} Ideally, the centroid of the ring would be defined based on the geometric center of the non-hydrogen atoms comprising that ring. However, given the improved agreement of the MM model with respect to both the QM data as well as in the MD simulations, this applied definition is suitable for modeling the cation- and anion-π interactions.

Molecular dynamics simulations

MD simulations were performed on eight protein systems that include cation- and anion-π pairs. Starting coordinates for all the protein structures were taken from the Protein Data Bank.⁹² Systems include protein GB3 domain (PDB: 2IGD, to be published), protein GB1 domain (PDB:2QMT)⁹³, basic fibroblast growth factor (PDB:1BFG),⁹⁴ DNA repair protein HHR23A (PDB:1F4I),⁹⁵ hen egg white lysozyme (PDB: 6LYT),⁹⁶ DNA methyltransferase 1 associated protein 1 (DMAP1) (PDB: 4IEJ, to be published), turkey egg lysozyme (PDB: 135L),⁹⁷ and a 12-residue beta hairpin, HP (PDB: 2EVQ).⁹⁸ The protein coordinate and structure files were initially prepared in CHARMM additive formats using the Solvator module in the CHARMM-GUI.⁹⁹ The resulting additive coordinate and structure files were then submitted to the Drude Prepper module in the CHARMM-GUI to obtain files in Drude format. For each system, the Drude-2013 protein force field¹⁰⁰ was used for the proteins with or without the parametrized atom pair-specific LJ parameters (NBFIX in CHARMM nomenclature).

Each system was solvated in a cubic box with a 10 Å minimum distance between the edge of the box and the protein. The SWM4-NDP model¹⁰¹ was used for water and Na⁺ or Cl⁻ ions^{102, 103} were added to neutralize the systems. Equilibrations were carried out using NAMD.⁸⁸ The extended Lagrangian approach with a dual-Langevin thermostat was used for integrating the equations of motion, where the temperature was maintained at 300 K for real atoms and at 1 K for Drude oscillators with thermostat friction coefficients of 5 ps⁻¹ and 20 ps⁻¹ respectively.⁸⁹ SHAKE was used to fix bonds involving hydrogen atoms.¹⁰⁴ Short-range LJ forces were switched to zero from 10–12 Å.¹⁰⁵ Electrostatic interactions were computed with the smooth particle mesh Ewald (PME) method with a real space cutoff of 12 Å, a kappa factor of 0.34 and a 6-order spline.^{106, 107} Each system was equilibrated under an NPT ensemble, where the pressure was set at 1 atm using Langevin piston pressure control with a piston oscillation period of 200 fs and a relaxation time of 100 fs. A 100 ps equilibration was performed with a 0.5 fs time step with all heavy atom restrained using a harmonic force constant of 1 kcal/mol Ų. Following equilibration, restraints were removed and production simulations were carried out using OpenMM.^{90, 91} The parameters for production simulations were similar to those used in equilibration with the following differences. The simulations were carried out for 100 ns with the velocity Verlet integrator using a 1 fs time step. The pressure was maintained at 1 atm using the Monte Carlo barostat with pressure changes attempted every 25 steps. The Drude hard wall constraint was set at 0.25 Å.⁷³ All analyses were carried out using facilities within CHARMM.^85–87

Preparation of Experimental Target Data

To perform an unambiguous protocol for selecting cation-π pairs of amino acids from protein crystal structures, the CaPTURE program¹ was used. This program was developed to identify energetically significant cation-π interactions within proteins and has been widely used in the study of cation-π interactions. To retrieve the target geometrical information, the PDB code of each protein system was submitted to CapTURE from which all the reported energetically significant cation-π interaction residue candidates were chosen as target data. The distances from the reported cation-π pairs were subsequently calculated, including the distance between the CZ carbon of Arg or NZ nitrogen of Lys and the geometric center of the aromatic six-membered ring of Phe, Tyr, or Trp. As CapTURE program does not report the cation-π interaction residues involving histidine, these residues were chosen if the cation-π pairs have interaction distances less than 6 Å based on the geometric center of the imidazole ring and the CZ carbon of Arg or NZ nitrogen of Lys in the crystal structure, indicating residue pairs that potentially participate in cation-π interactions. Similarly, residues between Phe, Tyr, Trp or His and Asp or Glu that have anion-π interaction distances less than 6 Å in the crystal structure were chosen. For protein structures determined by NMR, the distances from the all NMR resolved models were collected for comparison with the MD data.

Results

Interaction Energies

Atom pair-specific LJ parameters, including virtual particles treated as lone pairs at the approximate centroid of aromatic rings for each cation-π and anion-ring pair were optimized targeting minimum interaction energies for multiple local QM optimized interaction geometries. Examples of the starting interaction geometries used to perform QM optimization are illustrated in Figure 2, where the aromatic group is BENZ, molecular ions serving as cations are MAMM, MGUAN or IMIM, and the molecular ion serving as an anion is ACET. For other aromatic molecules, the starting interaction geometries were defined in a similar fashion. These orientations were the basis of rigid scans that directly probed the interactions of the cations and acetate with the π cloud of the ring systems, corresponding to approach 1. The obtained minimum interaction energies and distances from both the QM and the MM scans are presented in Tables S1 and S2 for the original Drude-2013 and the optimized Drude-2013-CP models, respectively. Subsequently, the minimum energy orientations from the rigid QM scans were used as the starting orientations for full QM optimizations, corresponding to approach 2. The optimized QM geometries for each complex are included in Table S7 of the supporting information. In a number of cases the optimizations identified more than one minimum, such that multiple geometries associated with the minima are presented. All minima are listed in Tables S3 and S4.

Figure 2.

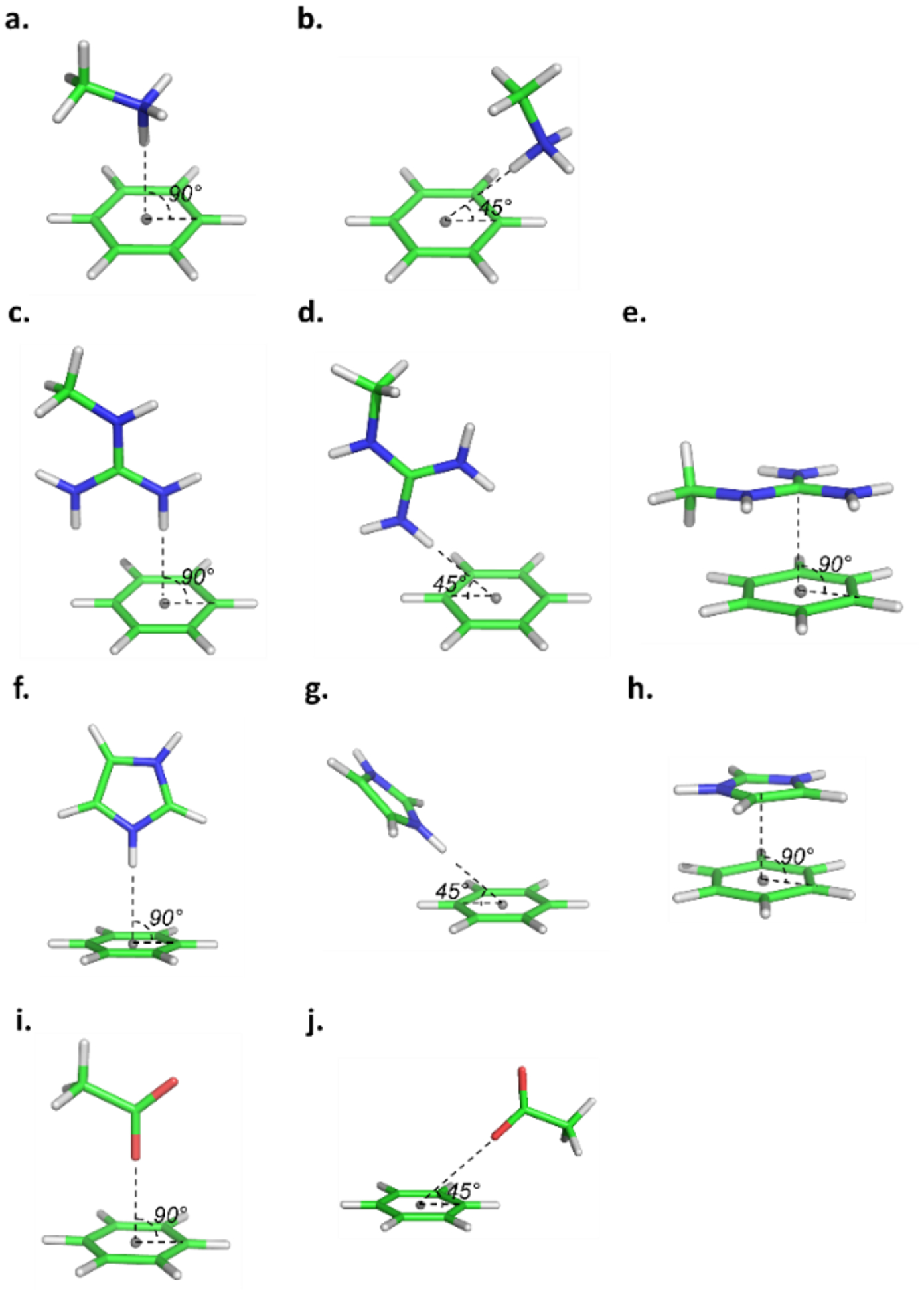
Illustrations of the starting interaction geometries between benzene and charged protein model compounds for QM optimization, where the cations are MAMM in a-b, MGUAN in c-e, IMIM in f-h, and the anion is ACET in i-j, where the cation/anion moves towards the lone pair (gray point) at the center of the aromatic ring, with angle being 45 or 90°.

As reported in a previous study,⁴⁸ as interaction energies computed based on SAPT2+/aug-cc-pVDZ model chemistry compare well with CCSD(T)cc-pV5Z, the former model chemistry was chosen to serve as the target QM data in this work. Given that the RIMP2 level of theory with the cc-pVQZ basis set⁷⁸ has been typically used to calculate interaction energies for parametrization of Drude small molecules,^{68, 66, 108, 109} this model chemistry was used as well for comparison. Comparison of QM interaction energies is shown in Tables S3 and S4 for the fully optimized approach 2 geometries. Results show that interaction energies of aromatic groups with cations computed based on MP2/cc-pVQZ are on average 1.3 kcal/mol more favorable than those computed from SAPT2+/aug-cc-pVDZ, while with an anion, energies from RIMP2/cc-pVQZ are on average 1.1 kcal/mol less favorable for the fully optimized complexes (Table 1). Comparison of the approach 1 rigid vs fully optimized approach 2 interaction energies shows a significant increase in the energies upon full optimization. While such a change was anticipated the magnitude was larger than expected. For example, the average RMP2/cc-pVQZ cation-π interactions went from −12.5 to −23.9 kcal/mol in approaches 1 and 2, respectively (Tables S1 and S3). In the case of the anion-based interactions the change was from −2.7 to −25.9 kcal/mol. These changes were due to the interactions optimizing hydrogen bond interactions that, in the case of the anions, typically lead to an approximately planar interaction of acetate with a CH, NH or OH moiety depending on the aromatic compound. Example of the fully optimized interactions of methylammonium or acetate with benzene and phenol are shown in Figure S1. As may be seen with the cations, the interaction with the π system is still present though favorable interactions with the hydroxyl of phenol are evident. With the anion-ring systems, while the geometry optimizations started with idealized anion-π interactions (Figure 2) upon full optimization the interaction orientations shifted to approximately planar interactions with the acetate oxygens directly interacting with the ring hydrogens or other functional groups (Figure S1). The contribution of hydrogen-bond interactions to the cation-π and the in-plane interactions of the anion-ring interactions lead to the interaction energies becoming significantly more favorable upon going from the rigid to fully optimized complexes. Given that the goal of the present study was to optimize the interactions of cations and anions with ring systems present in proteins which are expected to be dominated by the most favorable types of interactions, the parameter optimization focused on the fully optimized geometries, with those parameters subsequently applied to the rigid approach 1 geometries to evaluate the impact on the complexes dominated by pure interactions with the π systems of the rings.

Table 1.

Statistical comparison of the Drude-2013 protein force field without NBFIX (Drude-2013) and with NBFIX (Drude-2013-CP) computed minimum interaction energies (E_min, kcal/mol) with QM data for all the cation and anion-π systems. Presented are average differences (AVG) and standard errors of the differences (SE), absolute unsigned error (AUE), and root-mean-square differences (RMSD) without or with NBFIX compared with their QM target data obtained from RIMP2/cc-pVQZ (MP2) and SAPT2+/aug-cc-pVQZ (SAPT2+). Individual interaction results are shown in Table S3–S4. QM difference is between the two selected model chemistries.

	Drude-2013		Drude-2013-CP		QM difference
Fully optimized approach 2 interactions
Differences Compared to QM	MM-MP2	MM-SAPT2+	MM-MP2	MM-SAPT2+	SAPT2+-MP2
Cation-π (128 interactions)
AVG	2.78	1.44	1.89	0.55	1.34
SE	3.81	3.99	0.22	0.23	0.08
AUE	3.63	3.02	2.61	2.18	1.37
RMSD	4.71	4.22	3.12	2.70	1.63
Anion-π (29 interactions)
AVG	3.59	4.71	0.79	1.86	−1.11
SE	3.15	3.19	0.55	0.57	0.17
AUE	4.25	4.91	2.56	2.94	1.37
RMSD	4.74	5.65	3.16	3.66	1.42

Units are in kcal/mol

To optimize the cation-π and anion-ring interactions, we introduced atom pair-specific LJ parameters (NBFIX).⁷⁷ Initially, the NBFIX parameters were applied only between aromatic carbons and selected non-hydrogen atoms of the cations (e.g. carbon of MGUAN, nitrogen of MAMM, or carbons and nitrogens of IMIM); however, with this strategy there was a poor balance between the interactions of BENZ or TOLU with cations, PHEN or CRES with cations, and INDO or MIND with cations due to the shared atom types of the aromatic carbons. To differentiate between these aromatic molecules (i.e. BENZ and TOLU, PHEN and CRES and INDO and MIND), NBFIX terms were added between a virtual particle located at the center of the aromatic ring and the non-hydrogen atoms of the cations (as listed above) or anion (e.g. oxygen of ACET). This approach results in an improved representation of stacking and in-plane ring interactions; for example, the cation-π interaction between aromatic molecules and MGUAN or IMIM were improved (i.e. orientations e and h in Figure 2). In most cases the NBFIX parameters between the virtual particle and the non-hydrogen atom directly interacting with the virtual particles were added (eg. N in MGUAN as in orientations c and d in Figure 2) though in the case of MGUAN NBFIX between the central carbon and the virtual particle were added (ie. orientation e in Figure 2). In total, 39 optimized NBFIX parameters were applied. The overall differences compared to the QM target data with and without NBFIX are summarized in Table 1, which indicates that the resulting NBFIX parameters yield better agreement for the fully optimized approach 2 interactions with their target QM values computed at both the MP2/cc-pVQZ and SAPT2+/aug-cc-pVDZ model chemistries. Note that targeting simply one QM local optimized interaction geometry for a given interacting pair may not be sufficient, as the Drude interaction energies are more or less favorable (Table S3–S4) for the individual interaction orientations, such that when taking multiple geometries into account their individual energies were compromised for each cation- and anion-π geometry during the parametrization. In the case of the approach 1 rigid interactions, the optimized parameters also yielded overall good agreement with the cation-π interactions, with a slight degradation with respect to the SAPT2+ data. With the anion-π interactions there was a slight improvement in the SAPT2+ data with a degradation with respect to the MP2/cc-pVQZ data. However, this small level of poorer agreement was deemed acceptable as the interactions associated with the fully optimized structures, which are significantly more favorable, where improved.

Molecular dynamics simulations

Simulations were performed on eight peptide and protein systems. To validate the Drude-2013 FF with the optimized NBFIX parameters for cation- and anion-π interactions, referred to as Drude-2013-CP FF, analysis focused on the distance distributions between the ions and the centroid of the rings as shown in Figure 3 and Figures S2–S8 with distances obtained from the experimental structures. All the validation systems were run with the polarizable Drude-2013 FF along with the new Drude-2013-CP model. An example of one of the systems, the HP7 peptide, is shown in Figure 3. The peptide contains a Lys1-Trp10 cation-π pair near the terminus. As the peptide was obtained from NMR spectroscopy, all the NMR models (43 models) were used for comparison (blue bars in Figure 3). Normalized distance distribution of the cation-π pair shows that with the Drude-2013-CP FF the cation-π interaction distance distribution is more similar to those obtained from the NMR structures, whereas with the Drude-2013 FF the distance distribution is much wider, with a majority of the cation-π interaction distance being longer than 10 Å, indicating the cation-π interaction is not well represented.

Figure 3.

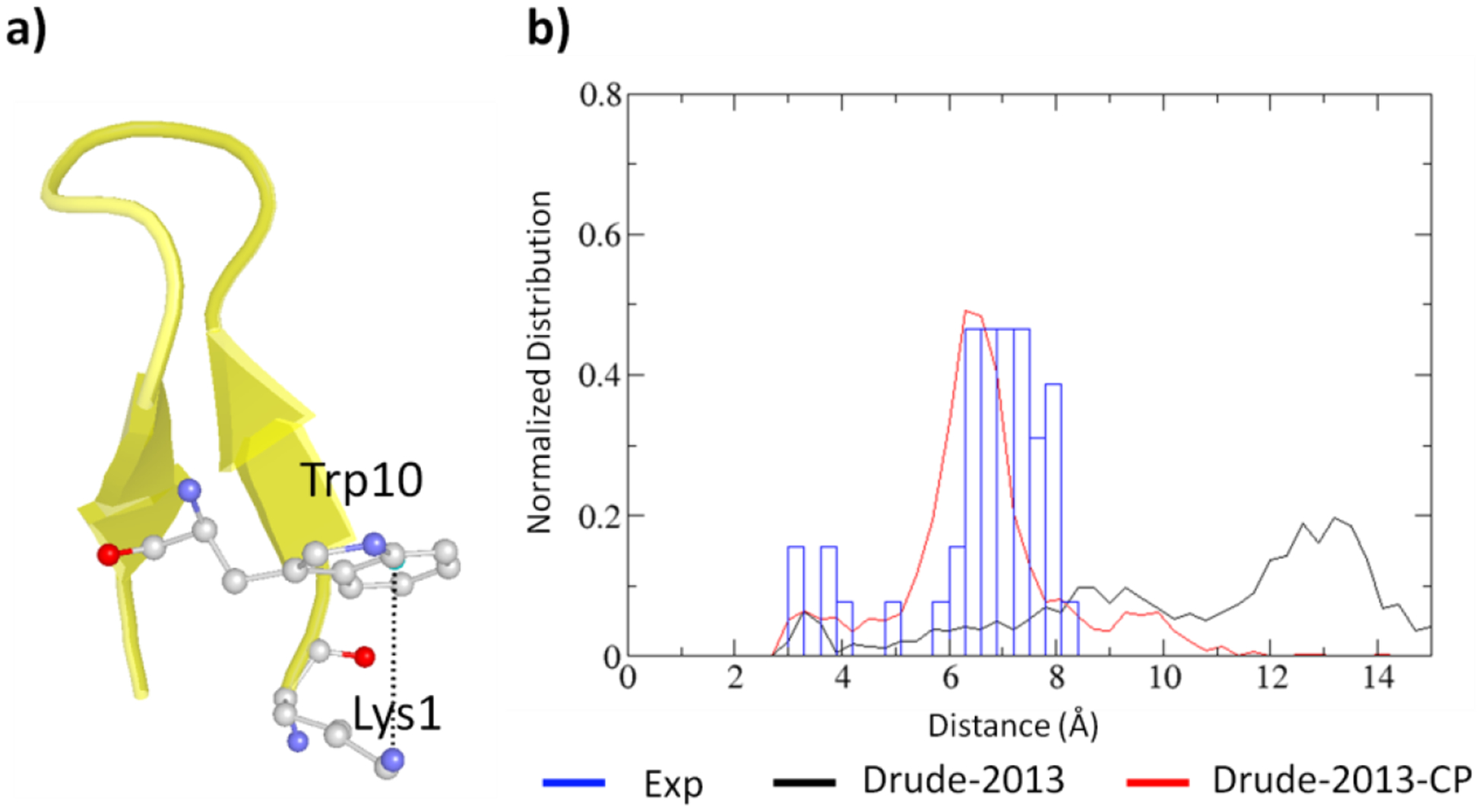
Analysis of the cation-π interaction in HP peptide (PDB:2EVQ). a) Structure of the peptide with the analyzed Lys1-Trp10 cation-π pair, where oxygen is in red, nitrogen in blue, carbon in white, and water molecules are not shown. b) Normalized distribution of the distances between the 6-membered ring center of Trp10 and the side chain nitrogen of Lys1 computed from simulations without NBFIX (Drude-2013, black) and with NBFIX (Drude-2013-CP, red) compared to those computed from NMR structures (Exp, blue).

Analysis of the remaining complexes in Figures S2 to S8 of the supporting information shows them to encompass a range of cation- and anion-π interactions as required to assure that a diverse range of interactions were being tested. In the figures, cation- and anion-π distance distributions from the MD trajectories are compared with individual distances from the X-ray structures or the distance distributions from the NMR structures. The average deviations of the cation- and anion-π interaction distances obtained from the MD simulations based on the original Drude-2013 and developed Drude-2013-CP FFs are summarized in Table 2. While in the simulations of DNA repair protein (PDB: 1F4I), cation-π interaction distances were poorly reproduced with both the original or optimized FFs, for the rest of systems better agreement with the experimental structure was achieved in all but 4 of the remaining interactions (Table 2 and Figures S2 to S8). Similarly, the Drude-2013-CP model significantly better reproduced the anion-π interactions than the original Drude-2013 except 3 interactions from the systems of PDB:1BFG and 4IEJ (Table 2 and Figures S2 to S8). Note that while we name these “anion-π interactions”, hydrogen bonds contribute to the interactions, particularly in the Asp/Glu (COO⁻) with Tyr (-OH) pairs; however, as the parametrization of the NBFIX parameters targeted the fully optimized QM geometries the contribution from the hydrogen bond interaction is taken into account, such that these types of anion-π interactions are overall improved.

Table 2.

Summary of the average cation- and anion-π distance (Å) deviations of the cation- and anion-π pairs (Table S4) compared to those from experimental structures for all eight protein systems (Exp), with average differences (AVG), absolute unsigned error (AUE), and root-mean-square differences (RMSD).

Cation-π interactions
PDB	#	Exp	Drude-2013		Drude-2013-CP
			Distance	Diff(Drude-Exp)	Distance		Diff(Drude-Exp)
2IGD	1	5.36	9.40±4.03	4.04	6.76±1.23	1.40
2QMT	1	5.43	7.10±1.74	1.67	6.17±1.17	0.74
1BFG	1	4.10	6.35±1.54	2.25	5.61±1.75	1.51
	2	4.90	5.11±0.59	0.21	4.95±0.57	0.05
	3	6.71	6.85±1.25	0.14	5.87±1.44	−0.84
	4	5.27	4.99±0.75	−0.28	5.52±0.98	0.25
	5	4.63	5.22±0.61	0.59	4.75±0.53	0.12
	6	4.59	4.44±0.36	−0.15	4.72±0.40	0.13
1F4I	1	3.94	7.16±2.09	3.22	6.29±0.69	2.35
6LYT	1	4.17	4.75±0.84	0.58	5.11±0.64	0.94
	2	3.54	6.78±1.85	3.24	4.70±1.15	1.16
	3	4.94	6.87±1.48	1.93	5.31±0.79	0.37
	4	5.44	5.73±0.64	0.29	7.69±2.12	2.25
	5	5.68	8.76±3.59	3.08	7.13±1.04	1.45
	6	4.35	6.62±1.35	2.27	5.80±1.24	1.45
4IEJ	1	5.30	6.45±1.33	1.15	5.78±0.75	0.48
	2	3.90	6.27±2.54	2.37	3.87±0.28	−0.03
	3	5.34	5.56±0.71	0.22	4.78±0.87	−0.56
	4	5.57	7.35±1.64	1.78	5.96±0.67	0.39
135L	1	4.09	8.16±1.99	4.07	7.56±1.22	3.47
	2	4.27	5.66±0.65	1.39	4.96±0.84	0.69
	3	5.34	12.2±2.37	6.86	7.16±1.07	1.82
2EVQ	1	6.62	11.39±3.88	4.77	5.85±.39	−0.77
AVG			1.99 ±0.41		0.82±0.21
AUE			2.02		1.02
RMS			2.66		1.33
Anion-π interactions
PDB	#	Exp	Drude-2013		Drude-2013-CP
			Distance	Diff(Drude-Exp)	Distance	Diff(Drude-Exp)
2IGD	2	5.13	9.404.03	4.27	6.76±1.23	1.63
2QMT	2	5.06	6.42±1.36	1.36	4.87±0.56	−0.19
1BFG	7	4.75	9.01±1.42	4.26	9.20±1.54	4.45
	8	4.70	6.06±0.55	1.36	6.42±0.47	1.72
1F4I	2	5.10	7.62±2.54	2.52	5.60±0.40	0.50
6LYT	7	5.37	8.62±1.36	3.25	5.74±0.27	0.37
	8	4.78	6.47±0.81	1.69	5.57±0.72	0.79
4IEJ	5	5.68	8.43±0.97	2.75	5.90±0.19	0.22
	6	5.27	8.43±0.97	3.16	5.90±0.19	0.63
	7	5.46	6.82±1.53	1.36	7.98±3.15	2.52
	8	5.46	8.44±3.84	2.98	5.77±1.06	0.31
	9	4.56	7.57±2.43	3.01	4.70±0.81	0.14
	10	3.98	5.58±0.66	1.60	4.99±0.60	1.01
135L	4	4.72	5.26±0.57	0.54	5.01±0.46	0.29
	5	5.27	6.11±0.89	0.84	5.35±0.30	0.08
AVG			2.33 ±0.34		0.96 ±0.31
AUE			2.33		0.99
RMS			2.59		1.52

Additional analysis included the calculation of the solvent accessible surface (SASA) of the ion-π pairs using a 1.4 Å solvent probe radius (Table 3). Qualitatively, there is a decrease of the SASA between the cation- and anion-π pairs with Drude-2013-CP FF than that occurring with the Drude-2013 FF with the exception of a slight increase of the anion-π pairs in PDB:1BFG system, indicating that the individual moieties in each cation- and anion-π pair are in closer proximity to each other associated with their interactions becoming more favorable throughout the simulations with the optimized NBFIX parameters. Correspondingly, RMSF analysis of the side-chain non-hydrogen atoms of the cation- and anion-π pairs shows that the Drude-2013 FF generally has significantly larger RMSF (Figure S9), as compared to values based on experimental B-factors and to the Drude-2013-CP FF. Though in the hen egg white lysozyme (PDB:6LYT) and basic fibroblast growth factor (PDB:1BFG) systems a few of the cation- and anion-π pairs shows much larger RMSF with Drude-2013-CP, the reduction of the fluctuations for the cation- and anion-π pairs is evident in other systems, although this comparison with respect to the experimental values is confounded by the temperature and resolution of the individual systems. Interestingly, RMSD analysis performed on all the systems based on the backbone non-hydrogen atoms (Table 4) further shows that the Drude-2013-CP FF in general yields smaller differences with respect to the experimental structures, except for the systems of PDB:1F4I, 1BFG, and 2QMT where their average RMSDs are slightly larger, suggesting that the improved modeling of the cation- and anion-π interactions contributes to the overall stability of the protein structures.

Table 3.

Average solvent accessible surface areas (SASA, Ų) of all sidechain atoms of all the cation- and anion-π pair(s) of each system and RMS fluctuations of the SASA as well as differences (Diff) with respect to their values from experimental crystal or NMR structures (Exp).

Cation-π interactions
PDB	Exp	Drude-2013				Drude-2013-CP
		SASA	RMSF	Diff		SASA	RMSF	Diff
2IGD	464.1	555.0	51.1	90.9		499.0	21.0	34.9
2QMT	461.7	517.0	21.9	55.2		490.2	21.3	28.4
1BFG	453.7	469.9	16.8	16.1		466.0	18.4	12.3
1F4I	428.6	478.1	34.4	49.5		458.1	12.5	29.5
6LYT	465.5	508.5	30.0	43.1		480.6	19.6	15.1
4IEJ	462.3	507.5	40.7	45.3		470.7	15.9	8.4
135L	458.7	515.9	24.5	57.2		488.9	20.0	30.1
2EVQ	510.8	600.5	49.8	89.8		510.5	34.8	−0.3
Anion-π interactions
PDB	Exp	Drude-2013				Drude-2013-CP
		SASA	RMSF	Diff		SASA	RMSF	Diff
2IGD	562.3	490.9	37.7	−71.4		546.3	13.3	−16.0
2QMT	553.0	542.8	13.3	−10.2		555.4	5.6	2.4
1BFG	410.3	478.6	17.7	68.3		481.8	17.4	71.5
1F4I	428.9	484.1	39.8	55.2		439.9	10.0	11.0
6LYT	411.0	468.2	24.1	57.3		429.6	13.1	18.6
4IEJ	422.7	475.2	36.7	51.4		440.8	22.2	19.4
135L	420.1	431.9	17.8	11.9		420.9	9.1	0.9
2EVQ	NA

Table 4.

Average RMS differences (RMSD, Å) and average RMS fluctuations (RMSF) of all the residues with respect to the experimental crystal or NMR structures of the backbone non-hydrogen atoms (C, O, N, Ca) while the RMSF^a analysis was also performed for the side chain non-hydrogen atoms.

PDB	Drude-2013			Drude-2013-CP
	RMSD	RMSF	RMSFa	RMSD	RMSF	RMSFa
2IGD	2.93	1.94	2.46	1.96	0.86	1.26
2QMT	2.10	1.14	1.53	2.11	1.55	1.97
1BFG	1.32	0.78	1.17	1.34	0.80	1.20
1F4I	2.42	0.79	1.26	2.64	1.15	1.57
6LYT	2.15	1.22	1.49	1.86	1.05	1.33
4IEJ	2.24	1.66	2.34	1.66	1.02	1.63
135L	2.79	1.32	1.58	2.19	0.94	1.18
2EVQ	3.22	2.36	3.10	1.47	0.96	1.47
Average	2.40	1.40	1.87	1.90	1.04	1.45

Conclusion

Presented are optimized polarizable Drude-2013 FF parameters for the cation- and anion-π interactions in proteins, referred to as Drude-2013-CP FF. The improvement was implemented using atom pair-specific LJ NBFIX parameters in conjunction with the inclusion of virtual particles at the centroids of aromatic rings. These NBFIX parameters were developed to improve the ion-π interactions between protein aromatic and charged side chains and termini by targeting QM optimized interaction energies of aromatic and charged model compounds representative of functional groups in proteins. The optimized model shows significant improvements against the majority of the target QM data for the fully optimized orientations. In the case of the cation and anion-π interactions there was a small degradation in the rigid, approach 1 interactions that represent direct interactions with the π-systems of the rings. The resulting parameters were then evaluated in their ability to reproduce the ion-π interaction distances from experimental x-ray crystal or NMR structures. Results from MD simulations showed overall improvement in both the cation-π and anion-π interaction distances of eight protein systems in solution. Further analysis of cation-π solvent accessible surfaces and their RMSFs from MD trajectories shows that both the solvent accessible surfaces and RMSFs were reduced with the Drude-2013-CP FF with the modest exception of the solvent accessible surface in one anion-π system and RMSFs in a few cation-π pairs, indicating that the cation- and anion-π interactions were more accurately modeled. While the NBFIX parameters were developed in the context of proteins in this work, the present parameters will be applicable to analogous charged functional groups or aromatic systems in other classes of molecules. In summary, an improved model of the cation-π and anion-ring interactions for proteins is provided in the context of the classical Drude polarizable FF, which will facilitate investigations of macromolecules systems where such interactions are present.