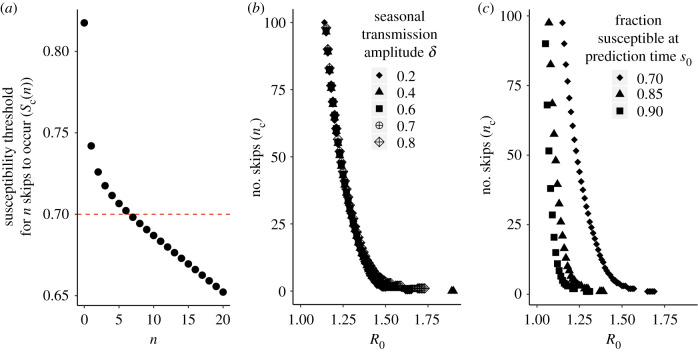
Figure 1.

(a) Graphical illustration of how the expected number of skips (n_c) is calculated. The black dots represent the threshold fraction of the population susceptible at the time of prediction required for n skips to occur (s_c(n)). The plot shows (s_c(n)) as a function of n (the number of skips) obtained from equation (2.1) with seasonality amplitude δ = 0.2 (contacts per person per day) and reproductive number R₀ = 1.4. In this example, the red line represents the fraction of the population susceptible at the time of prediction (s₀). If s₀ is smaller than s_c(n), at least n skips will occur. To find the expected number of skips (n_c), we identify the largest number of skips n such that s₀ is smaller than the susceptibility threshold required for those skips s_c(n). In this example, the red line intersects the s_c(n) curve between s_c(n = 6) and s_c(n = 7). Therefore, a critical skip number of n_c = 6 is obtained. (b,c) The critical skip value n_c as a function of R₀ for (b) different values of the amplitude of seasonal transmission δ with s₀ = 0.7, and (c) different values of the fraction of the population susceptible at the time of prediction (s₀) with δ = 0.70. In all three panels, the frequency of transmission ω, the population turnover rate μ and population growth rate r are fixed at respective values ω = (2π/365) d⁻¹ corresponding to an annual periodicity, μ = 1/(74.46 * 365) d⁻¹ corresponding to an average lifespan of approximately 75 years, and r = 1.55 µ d⁻¹ consistent with the growth of the city of Rio de Janeiro. These values were chosen for the purpose of illustration, based on the inverse of the average life expectancy in Brazil in 2012 according to the 2010 census [35], and the interpolation of population estimates for the resident population of the municipality of Rio de Janeiro from the 1991 [36] and 2000 [37] censuses assuming exponential growth.