Fig. 32.

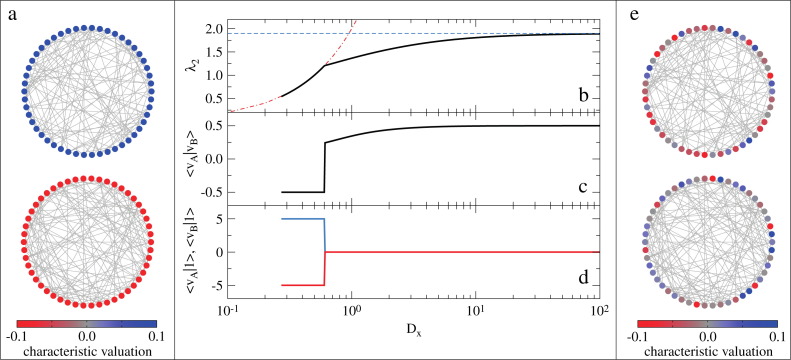
(Color online) Evolution of ${\lambda }_2$ and its associated eigenvector, $v_2$, as a function of $D_x$ for a multiplex composed of two Erdős–Rényi networks of $N=50$ nodes and average degree $\overline{k}=5$. In this example, the critical point is ${\left(D_x\right)}_c=0.602\left(1\right)$. (a) Values of the components in $v_2$ (characteristic valuations) for the nodes in the two layers for $D_x=0.602$ (just before the onset of the transition). (b) ${\lambda }_2$ as a function of $D_x$ (black line). The discontinuity of the first derivative of ${\lambda }_2$ is very clear. The transition between the two known different regimes ($2D_x$, blue dashed line, and $\frac{{\lambda }_2(L^A+L^B)}{2}$, red dash-dotted line) is evident. (c) Projection of $v_2^B$ into $v_2^A$ as function of $D_x$. (d) Projection of the unit vector into $v_2^A$ and $v_2^B$ as functions of $D_x$. These two projections indicate the sum of all components of $v_2^A$ and $v_2^B$ respectively. (e) Values of the components in $v_2$ (characteristic valuations) for the nodes in the two layers for $D_x=0.603$ (just after the onset of the transition).

Reprinted figure from Ref.  [96]. Courtesy of A. Arenas.