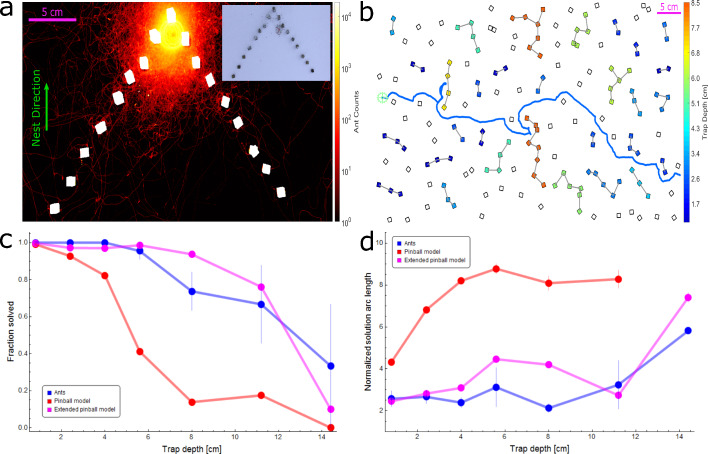
Figure 3. Simulation and ant performance near traps.

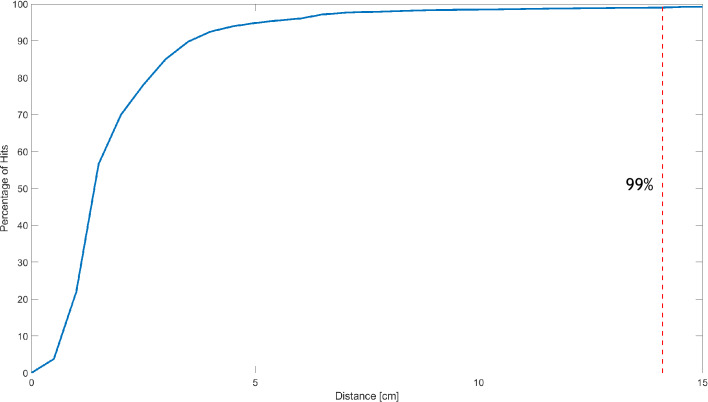
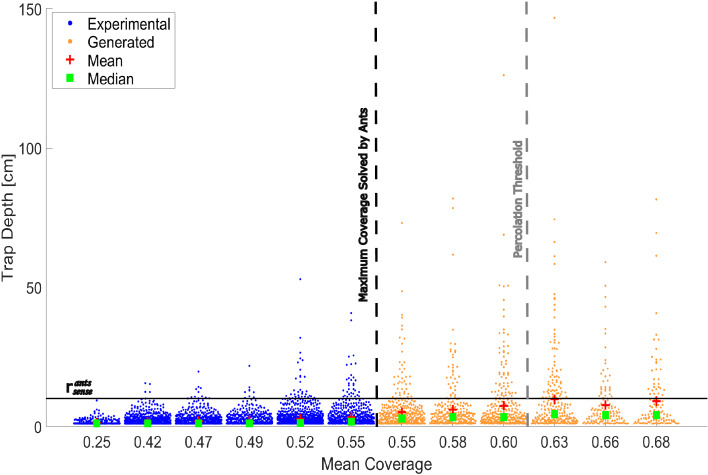
(a) Logarithmic heat map showing the spread of ants while the load is located near the deepest point of a triangular trap (extracted from 23 min of footage). The nest direction is towards the top. Color intensity represents the total number of ant counts within each 2D bin over the aforementioned experimental duration. A $r_{sense}^{ants}\cong 10\mathrm{cm}$ radius area centered on the load contains ∼99% of ant traffic in the vicinity of the load (see Figure 3—figure supplement 1). Inset shows an example image from the video footage of the experiment. (b) Illustration of traps on a sample maze. Each group of cubes comprising a trap are connected by gray lines and colored according to the trap depth in cm (as defined in Appendix 1.5) corresponding to the color bar. The empirical ant trajectory for this particular realization is plotted in blue (initial location marked using a pale green cogwheel). Nest direction is to the right. (C) Probability of trap solution as a function of trap depth for ants (blue), pinball model (red), and extended pinball model (magenta). Sample sizes (from shallow trap to deep): Ants - 73,70,35,22,19,6,3, Pinball Model - 2645,2886,1646,1289,982,343,105, Extended Pinball Model - 8979,8203,4637,3395,2042,815,403. (d) Average normalized arc length of the trajectory taken to solve a trap as a function of trap depth for ants and simulations (color scheme as in (c)). Trajectory lengths are normalized by trap depth (see Appendix 1.5, Materials and methods). Ant performance is approximately constant up to $D=12\mathrm{cm}$ cm which is on the scale of $r_{sense}^{ants}$ (see panel (a)). Sample sizes: Ants - 73,70,35,21,14,4,1, Pinball Model - 2620,2675,1352,530,136,60,0, Extended Pinball Model - 8952,7969,4497,3347,1913,620,302. Error margins in (c,d) are standard errors of the mean. Wherever no error is visible, the error is small enough to fit within the filled circle marker.

Figure 3—figure supplement 1. Cumulative ant spread.

Cumulative percentage of recognized ant counts as a function of distance from the center of the load (when it is located at the apex of the trap) in centimeters. The distribution reaches 99% at a distance of ∼14.1 cm (red dashed line), which is on the order of 10 cm.

Figure 3—figure supplement 2. Trap depth distributions.

Bee swarm plot displaying distributions of trap sizes as a function of mean coverage. Medians and means are represented by green rectangles and red pluses, respectively. The data is taken from experiments for coverage $\le 0.55$ (blue), and from computer generated mazes for coverage $\ge 0.55$ (orange). Solid black horizontal line represents the ants’ sensing radius $r_{sense}^{ants}=10$. Dashed black vertical line represents the maximal maze coverage the ants solved. Dashed gray line represents the percolation threshold of the system. Note that unsolvable traps were not included in the plot. For this reason, there is less data displayed for the very high coverage distributions.