How canyons evolve by incision into bedrock: Rainbow Canyon, Death Valley National Park, United States

Significance

The motion of tectonic plates gives rise to striking landforms. Canyons such as Rainbow Canyon near Death Valley are the products of tectonics operating over several million years. Tectonics has driven bedrock incision, canyon widening, and knickpoint migration. Here we capture these processes in a moving boundary model of canyon evolution. We treat bedrock incision in terms of abrasion caused by stones colliding with the bed. We estimate that based on present-day conditions, the knickpoint would have required 120,000 y to migrate to its current position. Rainbow Canyon offers a template for the understanding of canyons in general and how they deliver water and sediment to lowlands.

Abstract

Incising rivers may be confined by low-slope, erodible hillslopes or steep, resistant sidewalls. In the latter case, the system forms a canyon. We present a morphodynamic model that includes the essential elements of a canyon incising into a plateau, including 1) abrasion-driven channel incision, 2) migration of a canyon-head knickpoint, 3) sediment feed from an alluvial channel upstream of the knickpoint, and 4) production of sediment by sidewall collapse. We calculate incision in terms of collision of clasts with the bed. We calculate knickpoint migration using a moving-boundary formulation that allows a slope discontinuity where the channel head meets an alluvial plateau feeder channel. Rather than modeling sidewall collapse events, we model long-term behavior using a constant sidewall slope as the channel incises. Our morphodynamic model specifically applies to canyon, rather than river–hillslope evolution. We implement it for Rainbow Canyon, CA. Salient results are as follows: 1) Sediment supply from collapsing canyon sidewalls can be substantially larger than that supplied from the feeder channel on the plateau. 2) For any given quasi-equilibrium canyon bedrock slope, two conjugate slopes are possible for the alluvial channel upstream, with the lower of the two corresponding to a substantially lower knickpoint migration rate and higher preservation potential. 3) Knickpoint migration occurs at a substantially faster time scale than regrading of the bedrock channel itself, underlying the significance of disequilibrium processes. Although implemented for constant climactic conditions, the model warrants extension to long-term climate variation.

Here we study the morphodynamics of canyons incising into tablelands. By canyon, we do not mean simply a deep river valley incised into mountain terrain but explicitly “a long, deep, narrow steep-sided valley confined between lofty and precipitous walls in a plateau or mountainous area, often with a stream at the bottom" (1). Canyons operate by different rules than channel–hillslope complexes. Sediment is not provided by hillslopes but rather by canyon wall failure, in addition to the supply from an upland feeder channel. The upland–canyon transition is typically marked by an upstream-migrating knickpoint. Any morphodynamic treatment must cover 1) bedrock incision, 2) canyon wall collapse, 3) knickpoint migration, and 4) tectonics.

Fig. 1 A and B illustrate the generic problem, including canyon bed, canyon walls, knickpoint, feeder channel, and tableland. The problem includes uplift at rate υ or equivalently base level fall due to a normal fault along Panamint Valley. Fig. 1B illustrates the role of alluvial cover over bedrock, which can modulate abrasion-driven incision. We convert our generic example into a specific case in Fig. 1 C and D: the iconic Rainbow Canyon, United States, which drains the Argus Hills and flows into Panamint Valley. The Basin and Range Province of the southwest United States is home to many such canyons (2–5). We present a complete, quasi-predictive model of canyon evolution, as opposed to channel–hillslope evolution, that takes the salient features into account. Our model allows insight into the processes that drive incision, canyon widening, and knickpoint retreat. It adds to the general understanding of the topographic response to the generation of relief.

Fig. 1.

Configuration. (A) Schematic plan view shown a tableland, knickpoint, canyon walls, and canyon bed. (B) Schematic cross-sectional view showing the beds of the feeder channel and canyon, with partial alluvial cover. (C) Annotated plan view image © 2020 Google Earth showing Panamint Valley, Rainbow Canyon (section B‒C), and the Santa Rosa Wash (section A‒B). The head of the canyon is denoted as B, upstream of which is Santa Rosa Wash. The upstream and downstream ends of the study reach are denoted as A and C. (D) View of Rainbow Canyon looking downstream from Father Crowley Outlook, with Panamint Valley in the distance.

Fig. 1C shows the tableland of Rainbow Canyon; the canyon is in Fig. 1D. Further views are given in SI Appendix, Fig. S1. The overall setting is described in refs. 4 and 6.

Previous Modeling of Relevance

Three components play roles in V-shaped canyons incising into bedrock: alluvial morphodynamics, bedrock incision, and sidewall collapse. Alluvial morphodynamics is treated using a sediment transport capacity-based formulation with the Exner equation of sediment conservation (7, 8). Multiple mechanisms for bedrock incision exist (9–11). Here we treat bedrock incision in terms of the collision of alluvial clasts with a bedrock surface in a mixed bedrock–alluvial river (12, 13). The basis for this is the Macro-Roughness-based Saltation-Abrasion-Alluviation (MRSAA) formulation, which brings alluvial and abrasional bedrock morphodynamics into a common framework (14, 15). Comparative runs show that it suffices here to use the simpler Capacity Saltation Abrasion (CSA) model (12, 13). Our formulation includes the effect of alluvial cover on incision, in contrast to refs. 2, 16, and 17.

Researchers have considered alluvial (18) and bedrock (17, 19, 20) rivers subject to sidewall sediment input. Such a formulation was first developed for alluvial rivers (7, 21, 22). We adapt this formulation for a canyon containing a mixed bedrock–alluvial river. The closest antecedent to the present work (10) uses the CSA model (12, 13) to study sediment feed to a river from hillslopes in a region undergoing rock uplift. Summarizing the key features we bring together in this model, they are 1) a morphodynamic formulation for incision in mixed bedrock–alluvial channels, 2) a treatment of canyon sidewall collapse allowing study of long-term canyon morphodynamics, 3) a treatment of knickpoint migration, and 4) an account of the role of tectonics.

Rainbow Canyon: Site-Specific Information

As shown in Fig. 1C, Santa Rosa Wash flows eastward from point A to point B across the Argus Range tableland to the head of Rainbow Canyon. The reach, with a down-channel slope of 0.0156, is quasi-alluvial, with some bedrock. It extends much farther upstream (SI Appendix, Fig. S2), but the upstream end of the reach is taken at point A because the wash enters incised meandering farther upstream. Point B denotes the knickpoint at the entrance to Rainbow Canyon. The study reach extends from point A to point C, which is purposely chosen to be upstream of the normal fault at the entrance to Panamint Valley. Fig. 1D gives a ground view.

The morphodynamic modeling of tableland canyons offers a challenge. Fig. 1 A and B show that such a canyon has a V-shaped transverse section. This V shape is maintained by sidewall collapse as the channel incises.

The canyon region of our study reach extends eastward from its head (point B, 36°21′54.72″N, 117°34′14.59″W, in Fig. 1C) to somewhat upslope of where it spreads out as a fan on the bed of Panamint Valley (point C, 36°21′51.02″N, 117°31′12.63″W). This choice of downstream boundary makes it unnecessary to include fan deposition in the model. This reach has a down-canyon length of ∼5 km and average down-canyon bed slope of 0.094. The canyon walls narrow upstream, as seen in Fig. 1C. Panamint Valley is visible in the distance in Fig. 1D.

Channels feeding Rainbow Canyon drain from a catchment area of 200 km² (SI Appendix, Fig. S2). Only Santa Rosa Wash, which feeds into the canyon head, has been included. This channel has a gravel bed and sandy vegetated banks. We use a 3-km-long reach of Santa Rosa Wash from point A (36°23′18.51″N, 117°35′09.92″W) to point B of Fig. 1C, the head of Rainbow Canyon.

Theory and Model Setup

Flow and Capacity Sediment Transport Relation.

Our study reach includes a quasi-alluvial subreach (point A to point B in Fig. 1C) and a bedrock–alluvial subreach (point B to point C in Fig. 1C). We use the normal flow approximation of open channel flow (23) to compute the flow. Let B_b be width of bedrock channel, B_a be channel width at top of the alluvial layer, H be flow depth, S be down-channel slope of the top of the alluvial layer, Q_w be water discharge, g be gravitational acceleration, ρ be water density, and $\tau \hspace{0.17em}\text{be bed shear stress}$. Then $\tau =C_f{\left(Q_w/B_a/H\right)}^2=gHS$, where C_f = 1/(Cz)² and Cz is a dimensionless Chezy friction coefficient (7). We simplify the sediment to one grain size D and exclude particle abrasion. The alluvium has constant submerged specific gravity R (1.65). The Shields number ${\tau }^{\ast }$ is

$${\tau }^{\ast }=\frac{\tau }{\rho RgD}=\frac{HS}{RD}={\left(\frac{Q_w^2}{C{z}^{2}g{B}_a^2}\right)}^{1/3}\frac{S^{2/3}}{RD}.$$ [1]

We consider gravel bedload. The volume bedload transport rate/width is q_a, where the subscript denotes alluvium. The capacity transport rate q_ac (24) and the bedload transport rate over a surface with partial alluvial cover are

$$q_{ac}=4\sqrt{RgD}\hspace{0.17em}D{\left({\tau }^{\ast }-0.0495\right)}^{3/2},q_a=q_{ac}p\text{,}$$ [2]

where p denotes the areal fraction cover of bedrock by alluvium (12–15). The Exner equation of sediment conservation is

$$\left(1-{\lambda }_p\right)B_{a}p\frac{\partial {\eta }_a}{\partial t}=-I\frac{\partial }{\partial x}\left(B_a{q}_a\right),$$ [3]

where η_a is mean thickness of alluvial cover, I is flood intermittency, and λ_p is porosity of alluvium (14, 15). Eq. 3 corresponds to the MRSAA model (14, 15), which we simplify below.

Bedrock Morphodynamics.

We calculate the variation of bedrock elevation using (14, 15)

$$\frac{\partial {\eta }_b}{\partial t}=\upsilon -E,E=I\beta q_a\left(1-p\right).$$ [4]

Here $\upsilon \hspace{0.17em}\text{is rock}\hspace{0.17em}\text{uplift}\left(\text{or base level fall}\right)\text{rate}$, E is vertical erosion (incision) rate, and β is bedrock abrasion coefficient, which may vary (12) but here is constant.

Morphodynamics of Sidewall Failure and Canyon Widening.

Material from sidewall failure delivers sediment into canyon channels, likely episodically, due to rockfalls, landslides, undermining, etc. At long geomorphic time scale, failure can be abstracted to a continuous process that maintains approximately constant side slope S_s.

Fig. 2A shows a canyon cross-section, with bedrock channel width B_b and canyon side slope S_s. Where η_T denotes elevation to the canyon rim/top, the transverse width of one side of the canyon is B_s = (η_T − η_b)/S_s. Here canyon top width B_T = B_b + 2B_s, alluvial thickness is η_a, and alluvial width B_a = B_b + 2η_a/S_s. For the steep walls of Rainbow Canyon, for example, B_a ∼ B_b.

Fig. 2.

Schematization of sidewall configuration and morphodynamics of tableland canyons. (A) Parameters associated with canyon cross-section. The orange color denotes failed material. (B) Illustration of connection between sidewall failure and channel bedrock morphodynamics as the canyon evolves. Symbols are defined in the text.

When the bed incises over time $\mathrm{\Delta }\mathit{t}$, the depth of vertical incision is E$\mathrm{\Delta }$t or from Eq. 4, $\upsilon \mathrm{\Delta }\mathit{t}-\mathrm{\Delta }$η_b (Fig. 2A). From Fig. 2A, the canyon top uplifts a distance $\upsilon \mathrm{\Delta }t$. Thus, the volume per unit streamwise length per unit time of material input I_s to the channel due to sidewall failure corresponds to twice the shaded area in Fig. 2A:

$$I_s=2f_b{B}_s\left(\upsilon -\frac{\partial {\eta }_b}{\partial t}\right)=2f_b\frac{{\eta }_T-{\eta }_b}{S_s}I\beta q_a\left(1-p\right).$$ [5]

Here f_b is the fraction of failed material that does not break down to wash load. With the above and Fig. 2B in mind, Exner Eq. 3 is amended with Eq. 5 to

$$\left(1-{\lambda }_p\right)B_{a}p\frac{\partial {\eta }_a}{\partial t}=-I\frac{\partial }{\partial x}\left(B_a{q}_a\right)+2f_b\frac{{\eta }_T-{\eta }_b}{S_s}I\beta q_a\left(1-p\right).$$ [6]

The CSA model of bedrock–alluvial incision morphodynamics is used here, so it is not necessary to track the time variation of alluvial thickness (∂η_a/∂t). Assuming constant alluvial width B_a, dropping the relevant term in Eq. 6, and using Eq. 2, we obtain the relation below for the downstream increase in sediment load due to sidewall collapse.

$$\frac{\partial q_a}{\partial x}=2f_b\frac{{\eta }_T-{\eta }_b}{B_a{S}_s}\beta q_a\left(1-\frac{q_a}{q_{ac}}\right).$$ [7]

Moving Boundary Formulation Capturing Knickpoint Migration.

In order to capture knickpoint retreat, we implement morphodynamic calculations in moving boundary coordinates (25). The distance from the origin to the knickpoint is s_k(t). If the alluvial reach (x = 0 to x = s_k; point A to point B in Fig. 1A) supplies sediment to the canyon head at constant rate q_af at its (constant) slope S_u,all, it should neither aggrade nor degrade. The knickpoint itself can migrate upstream in accordance with the incisional dynamics set out in ref. 14. Since, as outlined there, incisional information propagates only upstream, the alluvial reach upstream of the knickpoint is not directly affected by uplift; it simply gets shorter.

With this in mind, we calculate morphodynamics only in the canyon reach. We define moving boundary coordinates $\overline{x}=\left(x-s_k\left(t\right)\right)/\left(L-s_k\left(t\right)\right)$ and $\overline{t}=\text{t}$. The domain 0 ≤ $\overline{x}$ ≤ 1 extends from the canyon head (point B in Fig. 1A) to the downstream end of the reach (point C in Fig. 1A). The transformation to moving boundary coordinates, which uses Eqs. 7 and 4 and ($\overline{x}$, $\overline{t}$), is given in SI Appendix. The governing equations for alluvial cover and bedrock incision are

$$\frac{1}{L-s_k}\frac{\partial q_a}{\partial \overline{x}}=2f_b\frac{{\eta }_T-{\eta }_b}{B_a{S}_s}\beta q_a\left(1-p\right),\frac{\partial {\eta }_b}{\partial \overline{t}}-\frac{\partial {\eta }_b}{\partial \overline{x}}\frac{\left(1-\overline{x}\right)}{L-s_k}\frac{d{s}_k}{dt}=\upsilon -I\beta q_a\left(1-p\right),$$ [8]

where ds_k/dt denotes knickpoint migration speed:

$$\frac{d{s}_k}{dt}=\frac{-{E|}_{s_k}}{\left({S|}_{s_k}-S_{u,all}\right)}=\frac{-I\beta {\left[q_a\left(1-p\right)\right]|}_{s_k}}{\left({S|}_{s_k}-S_{u,all}\right)}.$$ [9]

We refer to the formulation specified by Eqs. 8 and 9 as the MOVING-PIGG (Moving boundary Panamint Incision by Gravel Grinding) model.

Site-Specific Background for the Modeling.

The system is assumed to uplift (or be subject to base level fall) at the constant rate $\upsilon$. As part of the initial conditions, we assume that from the initial canyon head upstream, the tableland is a modest vertical distance $\mathrm{\Delta }$H_i above the feeder channel but is horizontal downstream of the knickpoint (Fig. 1B).

Floods are rarely monitored in the arid Panamint region, so many parameters are based on loose realistic estimates. The study reach L is 8 km long. The mean bed slope S_u,all of the upper 3 km (alluvial Santa Rosa Wash) is 0.0156, and the mean bed slope of the lower 5 km (bedrock–alluvial Rainbow Canyon, i.e., section B–C in Fig. 1C) is 0.094. Based on field inspection, characteristic gravel size is 60 mm. The dimensionless Chezy friction coefficient of the bed Cz is estimated as 10, based on the resistance relations in refs. 7 and 26.

Alluvial channel width B_a is approximated as 20 m in Santa Rosa Wash (point A to point B in Fig. 1C). Although width variation can play a role in bedrock river morphodynamics (27, 28), here it is held constant.

Fig. 1 C and D show that the downstream end of the study reach is upstream of Panamint Valley, where the canyon empties to an alluvial fan. This allows a constant rock uplift rate $\upsilon$. The extensional tectonics of the Basin and Range Province in general and the Panamint and Death Valley Regions in particular is complex (3, 4), but a characteristic uplift rate $\upsilon$ for the adjacent Panamint Range is 3 mm/y (4). Canyon side slope S_s = 0.7 based on remote sensing.

As the site is ungaged, flood characteristics are estimated indirectly. Flood intermittency I is taken as 0.005, so that flood flows occur for 1.8 d per year. Flood discharge Q_w is estimated based on a width B_a of 20 m, bed slope S of 0.0156, and dimensionless Chezy resistance coefficient Cz of 10 in Santa Rosa Wash and the assumption of Froude-supercritical flow with Froude number Fr = 1.25, as is appropriate for a desert arroyo (29). Using the relations $\mathit{Fr}=U/\sqrt{gH}$ and U = Q_w/(HB_b), where U is flow velocity, in conjunction with Eqs. 1 and 2, we find Q_w = 29 m³/s, H = 0.51 m, U = 2.82 m/s, and q_ac = 0.00134 m²/s. We use 0.00134 m²/s as the gravel feed rate q_af at the knickpoint.

The discharge 29 m³/s at an intermittency of 0.005 with the drainage area of 200 km² gives a basin runoff rate of 23 mm/y. The capacity transport rate Q_ac = q_acB_a = 0.027 m³/s at an intermittency 0.005 corresponds to an annual sediment yield of 4.29 × 10³ m³/y or less than 1% of the sediment production rate by uplift (3 mm/y × 200 km² = 6 × 10⁵ m³/y).

The coefficient β in the abrasion–incision relation Eq. 4 is set at 0.015 km⁻¹. This corresponds to a travel distance of 139 km for a clast made of the same material as the bedrock to halve in diameter due to abrasion (14). This value was obtained in part by calibration.

The upstream end of the Santa Rosa Wash reach is at x = 0, and the downstream end of the canyon reach is at x = L = 8,000 m. We set the initial knickpoint position arbitrarily at s_k = 7,400 m. Thus, the initial canyon is only 600 m long. We set the initial canyon bed slope so as to exceed S_u,all for the last 600 m of the study reach, in correspondence with a mean present-day canyon slope S_d,bed of 0.094. The canyon top is parallel to and 5 m higher than the initial bed for the first 7,400 m $\left(\mathrm{\Delta }{\mathit{H}}_{\mathit{i}}=5\text{m}\right)$ and held horizontal farther downstream. The tableland configuration does not change except for uplift (Fig. 1B).

Conjugate Steady State and Alluvial Slopes.

Before studying the morphodynamics of canyon evolution, we study a related steady state problem. We consider the different steady states of two unconnected reaches, one purely alluvial (upstream corresponding to Santa Rosa Wash) and one bedrock–alluvial (downstream corresponding to Rainbow Canyon). Both have the same grain size D and submerged specific gravity R of alluvium, width of channel alluvium B_a ≅ width of bedrock channel B_b in the canyon, dimensionless Chezy resistance coefficient Cz, and flood discharge Q_w. The alluvial reach is unaffected by uplift, but the bedrock–alluvial reach incises at the same rate as rock uplift rate $\upsilon$. For simplicity we neglect sidewall failure and knickpoint migration here. The governing equations of the model allow the downstream reach to have a steeper steady-state slope S_d,bed than that of the upstream alluvial reach S_u,all, even though they have the same volume gravel transport rate/width q_a. This has implications for the morphodynamic analysis below.

The value of q_a is the capacity value for the alluvial upstream reach; between Eqs. 1 and 2,

$$q_a=4\sqrt{RgD}D{\left[{\left(\frac{Q_w^2}{C{z}^{2}g{B}_a^2}\right)}^{1/3}\hspace{0.17em}\frac{S_{u,all}^{2/3}}{RD}-0.0495\right]}^{3/2}.$$ [10]

The capacity transport rate in the bedrock-alluvial reach is

$$q_{ac}=4\sqrt{RgD}D{\left[{\left(\frac{Q_w^2}{C{z}^{2}g{B}_a^2}\right)}^{1/3}\hspace{0.17em}\frac{S_{d,bed}^{2/3}}{RD}-0.0495\right]}^{3/2}.$$ [11]

Assuming steady state in the bedrock–alluvial reach, Eq. 4 reduces with Eq. 2 to $\upsilon =I\mathit{\text{β}}{q}_a\left(1-q_a/q_{ac}\right).$ Using the same value q_a in the upstream and downstream reaches, Eqs. 10 and 11 give a predictive relation for S_d.bed as a function of S_u,all:

$$S_{d,bed}=a_2^{-3/2}{\left[\left(a_2{S}_{u,all}^{2/3}-a_3\right){\left(1-\upsilon {\left(I\beta a_1\right)}^{-1}{\left(a_2{S}_{u,all}^{2/3}-a_3\right)}^{-3/2}\right)}^{-2/3}+a_3\right]}^{3/2},$$ [12]

where $a_1=4\sqrt{RgD}\hspace{0.17em}D,a_2={\left(\frac{Q_w^2}{C{z}^{2}g{B}_a^2}\right)}^{1/3}\frac{1}{RD},\mathrm{and}\hspace{0.17em}{a}_3=0.0495$.

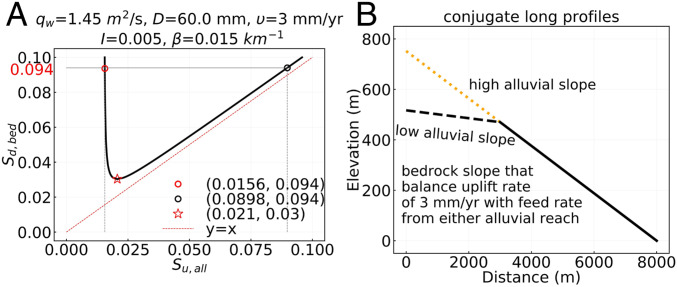
We plot the S_d,bed versus S_u,all in Fig. 3A; the values used for I, β, $\upsilon$, R, D, Q_w, B_a, and Cz are as specified above and given in SI Appendix, Table S1. It is seen that the curve admits double-valued behavior, in accord with the quadratic form p(1 − p) embedded in the model (12, 13). There is a minimum bedrock–alluvial slope S_d,bed = 0.030 for S_u.all = 0.021, below which no steady state is possible (see also ref. 30). Above this minimum, there are two conjugate alluvial slopes S_u,all associated with any given bedrock slope S_d,bed.. The conjugate slopes are delineated by a very narrow zone to the left of the minimum in Fig. 3A, within which S_d,bed can be substantially larger than S_u,all, and a much wider zone where S_d,bed is only modestly larger than S_u,all.

Fig. 3.

(A) Plot of steady-state downstream bedrock-alluvial slope S_d,bed versus upstream alluvial slope S_u,all. The minimum value of bedrock-alluvial slope at S_d,bed = 0.03 for S_u,all = 0.021. The left branch of the curve corresponds to cases like Rainbow Canyon, where the bedrock slope is substantially higher than the alluvial slope. The minimum value of S_d,bed (0.03) is at S_u,all = 0.021. (B) Illustration of the conjugate high alluvial slope (0.0898) and low alluvial slope (0.0156), which provides a sediment feed rate (0.0230 and 0.00134 m²/s, respectively) allowing the bedrock reach with slope 0.094 to be in balance with an uplift rate of 3 mm/y.

We consider $\upsilon =3\text{mm}/\text{yr}$ and S_d,bed = 0.094. The conjugate upstream alluvial conditions are 1) (S_u,all, q_af) = (0.0156, 0.00134 m²/s), with a canyon cover factor P = 0.055, and 2) (S_u,all,c, q_af,c) = (0.0898, 0.0234 m²/s), with a canyon cover factor P = 0.945. Any case describing configurations like Rainbow Canyon should fall to the left of the minimum in Fig. 3A, where the slope difference is large. The field value 0.094 was matched in the theoretical formulation by varying the abrasion coefficient β.

For illustrative purposes, two alluvial reaches, with the corresponding slopes 0.0156 and 0.0898, are plotted upstream of the bedrock reach with a slope of 0.094 in Fig. 3B. The bedrock reach would be in balance with uplift with either alluvial feed rate. Only one of these, i.e., the lower alluvial slope, corresponds to Santa Rosa Wash. The issue of the higher alluvial slope is examined in Discussion.

Results

Evolution from a Very Short Initial Canyon with No Sidewall Input.

We use MOVING-PIGG to model the evolution of Rainbow Canyon, including knickpoint migration. The initial conditions are in SI Appendix, Fig. S3. The length of the study reach (Fig. 1A) is 8 km; at present-day conditions, the upstream 3-km subreach is alluvial, and the downstream 5-km subreach is bedrock–alluvial. To start calculating, the bed elevation of the downstream end is assigned the constant value 0 m. The 600-m reach at the downstream end of the domain is given an initial slope of 0.094, in correspondence with the calculation in the section immediately above, as well as present-day measurements. We consider two subcases for the reach upstream of the initial knickpoint: one corresponding to the lower of the two conjugate slopes shown in Fig. 3A (S_u,all = 0.0156, q_af = 0.00134 m²/s) and one corresponding to the upper of the two (S_u,all,c = 0.0898; q_af,c = 0.0230 m²/s). The tableland is located 5 m above the bed of the initial wash but is held horizontal beyond the slope break to the downstream end.

Fig. 4 shows results for the case f_b = 0, no sidewall contribution to bed material load. Fig. 4A shows the low-feed case of the conjugate pair of Fig. 3A corresponding to our estimate of the current feed rate q_af = 0.0134 m²/s, and Fig. 4B corresponds to the higher conjugate feed rate q_af,c = 0.0230 m²/s.

Fig. 4.

Results of modeling of canyon evolution. (A) Canyon evolution with S_u,all = 0.0156 and (B) canyon evolution with S_u,all = 0.0898. These are conjugate alluvial slopes, both of which result in an equilibrium canyon bedrock slope S_d,bed = 0.094. The left-hand case has an alluvial slope in agreement with the present-day Santa Rosa Wash. In both cases, the equilibrium bedrock slope is maintained as the knickpoint migrates upstream.

In the case of Fig. 4A, the knickpoint retreats at 0.0393 m/y, reaching its present position in 120,000 y. It should be kept in mind that this is an estimate assuming that present conditions prevailed up to 120,000 y ago. During the intervening ice age, however, rainfall may have been higher, and Panamint Valley may have been partially filled by a lake (31). The knickpoint climbs 402 m over this 120,000-y period. Note that the initial slope for the 600-m-long initial canyon, which was chosen to be the observed value of 0.094, is maintained as the canyon evolves. In the case of Fig. 4B, the knickpoint retreats at 0.745 m/y, reaching its present-day position in 5,900 y. It rises 407 m over this period, while maintaining a bed slope of 0.094. The very small difference in alluvial versus bedrock slope, combined with the high speed of knickpoint retreat (∼20 times higher than the conjugate case), suggests that this case (right side of Fig. 3A) may be seen less commonly or for shorter periods in nature.

The abrasion coefficient β was calibrated in order to obtain an equilibrium bedrock–alluvial slope S_s,bed equal to the observed bedrock slope of 0.094. It is possible to obtain a range of values of β that yield this slope by calibrating with grain size D, holding other parameters constant. The results of such a calculation are in SI Appendix, Fig. S4. As D varies from 20 to 80 mm, β increases, and p and q_af decrease. The migration speed of the knickpoint ds_k/dt, however, remains nearly constant.

Evolution from a Very Short Initial Canyon with Sidewall Input.

We now consider the effect of sediment input from canyon sidewalls. We include calculations for f_b = 0 (all failed material breaks down to wash load) to f_b = 1 (all failed material breaks down to bedload). Fig. 5 A–D show results after 120,000 y, using input conditions corresponding to SI Appendix, Table S1, and q_af = 0.00134 m²/s (Santa Rosa Wash). Each plot shows results for the five cases f_b = 0, 0.25, 0.5, 0.75, and 1.

Fig. 5.

Results of calculations with fraction of sidewall material that contributes to bed material load f_b = 0, 0.25, 0.5, 0.75, and 1. All calculations use the same input parameters as those of Fig. 4A, i.e., Santa Rosa Wash. (A) Canyon long profiles, showing an autogenic knickpoint where slope suddenly decreases for each case f_b > 0. (B) Downstream variation in volume sediment transport rate/width q_a. (C) Downstream variation in cover fraction p. (D) Downstream variation in canyon top width B_T.

In Fig. 5A, the effect of sidewall input is confined to the lower part of the channel. The higher upstream slope and lower downstream slope are in general accordance with the data, but the model shows an autogenic knickpoint (10) that is not clearly reflected in the field. This knickpoint, which appears only for f_b > 0, corresponds to a sudden drop in bed slope. Fig. 5B shows that the sediment load increases downstream when f_b > 0; for the case f_b = 1, q_a at the downstream end is about five times the feed rate. Fig. 5C shows a sudden jump in cover fraction p from around 0.055 to in excess of 0.4 at the autogenic knickpoint. The numerical fluctuations reflect this discontinuity. Fig. 5D shows that the model generally captures the downstream variation in canyon top width, without strong dependence on f_b. Sidewall sediment input is seen to strongly increase the cover fraction downstream of the autogenic knickpoint.

Fig. 6 shows four three-dimensional snapshots of predicted canyon morphology corresponding to t = 0, 72,000, 96,000, and 120,000 y. The value of f_b used in the calculation is 0.75. Tableland uplift, canyon incision and widening, and knickpoint retreat are visualized in Fig. 6.

Fig. 6.

Three-dimensional views of predicted morphology of Rainbow Canyon at (A) t = 0 y, (B) t = 72,000 y, (C) t = 96,000 y, and (D) t = 120,000 y. The calculations are for f_b = 0.75.

It was shown (Fig. 4A) that a bedrock–alluvial channel slope of 0.094, i.e., the observed value, leads to an incision rate that balances an uplift rate of 3 mm/y, as long as the bed material feed rate equals that supplied by Santa Rosa Wash (0.00134 m²/s). When we use this value for an initial canyon 600 m in length, this canyon propagates upstream at the same slope, until the head reaches the observed position after 120,000 y.

It is of interest to know how the canyon would evolve if, holding all other parameters constant, the initial canyon slope were varied. SI Appendix, Fig. S5 A and B show canyon evolution using starting canyon slopes 0.05 and 0.15, respectively. In neither case does the initial canyon slope noticeably evolve toward the equilibrium value of 0.094. Instead, the initial canyon slope is simply propagated upstream. That is, the canyon slope shows no obvious tendency to relax toward the equilibrium value.

The slope in the model is, however, relaxing toward its equilibrium value, but the rate of relaxation is over an order of magnitude slower than knickpoint migration. This is seen in SI Appendix, Fig. S6 A and B, where we model the evolution of a canyon with a length of 8 km but with no knickpoint at the upstream end. Otherwise, all modeling conditions are the same as in SI Appendix, Fig. S5. In SI Appendix, Fig. S6A, the initial canyon has slope 0.05, and in SI Appendix, Fig. S6B, it has slope 0.15, in correspondence with SI Appendix, Fig. S5 A and B. In both cases, the canyon evolves to the equilibrium slope 0.094, but only after millions of years. This issue is discussed below.

Discussion

Our analysis argues for two conjugate knickpoint configurations. For the same downstream bedrock canyon reach incising in equilibrium response to uplift, there can be two upstream alluvial feed channel conditions. One of these typically has a slope that is much smaller than the bedrock canyon, and one typically has a slope that is only modestly smaller than the canyon. The latter case, although previously obtained from numerical modeling (14), does not seem to be common in the field. One reason for this is because knickpoints of the latter type retreat much more rapidly than the former type. This can be seen from Eq. 9: retreat velocity scales as E/(S_d,bed–S_u,all). In the latter case, alluvial slope S_u,all is only modestly smaller than canyon bedrock slope S_d,bed.

Fig. 4 shows that the predicted canyon profile has a constant bed slope 0.094, whereas the canyon profile in the field is upward concave. A more refined analysis of this issue might require a further consideration of the quite varied lithology of the Argus Hills (32), via, e.g., a varying abrasion coefficient β. Mechanisms in addition to abrasion, such as plucking, may play roles in setting canyon profile (10).

Field observations of the far upper canyon indicate the existence of two waterfalls, one of which has a plunge pool excavated into bedrock. The present model can capture neither waterfall nor plunge pool formation. A model is available, however, which treats the flow as unsteady shallow water flow and which can capture plunge pool formation (33).

Another factor which might contribute to downstream variation in slope is downstream fining of alluvium due to abrasion (34). The authors did not make observations of the downstream end of Rainbow Canyon. The bed at the mouth of the adjacent smaller but otherwise similar canyon, Little Rainbow Canyon in SI Appendix, Fig. S2, did not appear to be finer than that of the scree faces toward the upstream end of Rainbow Canyon. Fining of sediment mixtures due to abrasion can be incorporated into the model (35).

It was shown in SI Appendix, Fig. S5 A and B, that when the short starting canyon of the numerical calculation is given a slope that differs from the equilibrium one, this slope is barely modified by the time the knickpoint reaches its modern position, 120,000 y later. We show in SI Appendix, Fig. S6 A and B, that the initial slope does relax to its equilibrium value but only after the passage of ∼2 million y. This disparity in knickpoint migration speed and bed regrading speed can also be explained in terms of Eq. 9. The speed of bedrock slope regrading should scale as the incision rate E, whereas the speed of knickpoint migration should scale as E/(S_d,bed − S_u,all). For the conditions studied here, the latter is about an order of magnitude larger than the former.

Neither uplift nor sediment supply can be expected to be continuous. The case of a sedimentograph, or cyclically varying sediment supply (15), could be incorporated into MOVING-PIGG. This factor, in addition to lithological variability, multiple incision mechanisms, downstream fining, etc., should, however, arguably be omitted in a first-order model.

Our model represents a step beyond simple detachment-limited models (16, 36) in that the effect of cover on incision (12) is explicitly included. We also explicitly capture knickpoint migration. Large immobile blocks were not evident in Rainbow Canyon, but the model can be extended to include them (17, 20). Panamint Valley may have been partly filled by a lake during the Last Glacial Maximum (31). The MRSAA form of our model can handle this condition (14).

Conclusions

We apply a generic moving-boundary model of tableland canyon incision, MOVING-PIGG, to Rainbow Canyon, CA. Rainbow Canyon serves as a template for similar tableland canyons in the Basin and Range Province of North America and worldwide. Key model results follow.

For any downstream canyon that incises in balance with uplift, there can be two slopes (conjugate slopes) of upstream equilibrium alluvial channel that feed into it. In one case, the alluvial bed slope is much lower than the bedrock slope immediately downstream. In the other case, the alluvial bed slope is only modestly lower. Rainbow Canyon corresponds to the former, where the alluvial slope is 0.0156 and bedrock slope is 0.094. The time for the knickpoint to reach its present position is estimated to be 120,000 y.

The latter case, where the slope difference is small, may be rare in nature. In the case computed here, the knickpoint would reach its present position in only less than 8,000 y because the speed of knickpoint retreat scales inversely with the difference in slopes.

Sidewall material may fail to wash load or bed material load. Where f_b is the fraction of material that fails to bed material load, we performed calculations for f_b = 0 to 1. We found that the pattern of canyon width does not vary strongly with f_b, but the bedload transport rate and the areal fraction of alluvial cover increase downstream as f_b increases.

Most of the calculations were performed using a short starter canyon that had a slope of 0.094, the equilibrium value for the specified conditions. For the case of larger and smaller initial slopes, the slope should relax to the equilibrium value. However, in two cases (slope of 0.05 and 0.15), this did not happen over the 120,000 y for the knickpoint to reach its present position. Further calculations show that relaxation to equilibrium does indeed occur but only over 2 million y. The model explains this behavior: knickpoint migration rate scales as incision rate over slope. At the same time, however, this indicates that the processes establishing early canyon evolution are insufficiently explained by the model.

The model can be easily extended to include a depositional subsiding zone (e.g., Panamint Valley) downstream of the end of the present model. This would, however, necessitate the use of a morphodynamics model that can smoothly accommodate adjacent fully and partially alluviated reaches.

Our model provides a template for predicting long-term canyon incision, sidewall erosion, knickpoint erosion, and canyon extension into the uplands. It provides an essential piece to the big picture of landscape evolution that can be used to understand tectonic–climate–erosion and topographic–biologic interaction in tectonically active terrain prone to canyon formation.

Materials and Methods

The original data used in Figs. 3A, 4 A and B, 5 A–D, and 6 A–D are given as Dataset S1. The code used in the analysis (Panamint-PNAS.py) is available in the GitHub repository at https://github.com/lizhangpig/RainbowCanyonIncisionKnickpoint.