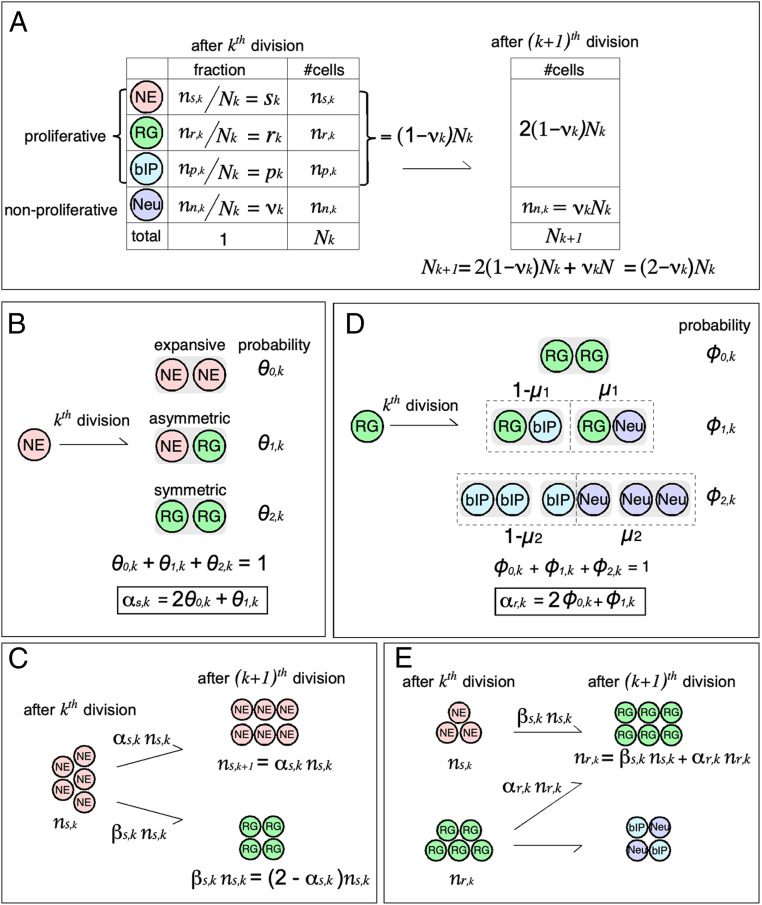
Fig. 3.

Graphical summary of the cortical development model. (A) Demographic of developing cortical neurons. The equation relating $N_k$ and $N_{k+1}$ is repeatedly used in the present theory to convert the number of each cell type to its fraction, which was experimentally measured. NE, neuroepithelium cell; RG, radial glia; bIP, basal intermediate progenitor; Neu, neuron derived from local cortical progenitor. (B) Three cell division modes of NE. A goal of the present model is estimate the average number of NEs generated by one mother NE at a given developmental stage, termed as the expansion coefficient (${\alpha }_{s,k}$). (C) Differentiation of NE at a cell division. ${\alpha }_{s,k}$ is a quantity determining change in the number of NEs at each division. (D) Cell division mode of RG. An RG yields two cells, which can be RG, bIP, or neuron. ${\mu }_1$ is the probability that, when an RG generates one non-RG cell, it will be a neuron. ${\mu }_2$ is probability that, when an RG generates two non-RG cells, either one will be a neuron (i.e., $2{\mu }_2$ is the expected number of neurons from one RG under this division mode). The expansion coefficient of RG (${\alpha }_{r,k}$) is defined in the same way as that of NE. (E) Origin of RGs. Because RGs are derived from NEs and RGs, the number of RGs after the $\left(k+1\right)$th cell division ($n_{r,k+1}$) is the sum of those from NEs (${\beta }_{s,k}{n}_{s,k}$) and RGs (${\alpha }_{r,k}{n}_{r,k}$). Note that ${\beta }_{s,k}=2-{\alpha }_{s,k}$.