Relaxation Times of Ligand-Receptor Complex Formation Control T Cell Activation

Abstract

One of the most important functions of immune T cells is to recognize the presence of the pathogen-derived ligands and to quickly respond to them while at the same time not responding to its own ligands. This is known as absolute discrimination, and it is one of the most challenging phenomena to explain. The effectiveness of pathogen detection by T cell receptor is limited by chemical similarity of foreign and self-peptides and very low concentrations of foreign ligands. We propose a new mechanism of how absolute discrimination by T cells might function. It is suggested that the decision to activate or not to activate the immune response is controlled by the time to reach the stationary concentration of the T-cell-receptor-ligand-activated complex, which transfers the signal to downstream cellular biochemical networks. Our theoretical method models T cell receptor phosphorylation events as a sequence of stochastic transitions between discrete biochemical states, and this allows us to explicitly describe the dynamical properties of the system. It is found that the proposed criterion on the relaxation times is able to explain available experimental observations. In addition, we suggest that the level of stochastic noise might be an additional factor in the activation mechanisms. Furthermore, our theoretical approach explicitly analyzes the relationships between speed, sensitivity, and specificity of T cell functioning, which are the main characteristics of the process. Thus, it clarifies the molecular picture of T cell activation in immune response.

Significance

Immune response is the main tool for cells to defend against diseases. Its central part is a T cell activation, which takes place after binding of an antigen to the corresponding receptor. The process is unique because T cells must distinguish between foreign peptides, which are present in small amounts, and chemically similar self-ligands, which are present in large quantities. We propose a, to our knowledge, new hypothesis on the discrimination mechanism. It argues that the activation is governed by the relaxation times to reach the stationary concentrations of T cell-antigen complexes. We show that these times are short for self-ligands, whereas for long relaxation times, the immune response is activated. Theoretical calculations agree with experimental observations.

Introduction

T cells are essential components of the adaptive immune system, and they play a central role in detecting and responding to various diseases in healthy organisms (1,2). Activation of T cells relies on binding between a T cell receptor (TCR) and its peptide major histocompatibility complex (pMHC) on the surface of antigen-presenting cells. The inappropriate activation of T cells toward self-peptides and endogenous antigens leads to serious allergic and autoimmune responses (2). It is known that two main factors can complicate the successful T cell functioning. First, chemical similarity of self-peptides and foreign peptides makes it very difficult for the T cell to elicit proper responses toward the right targets. Second, the concentrations of self-peptides in cells is known to be several orders of magnitude larger than the concentrations of foreign peptides (3, 4, 5). The problem is that the T cells must identify very few foreign ligands in the “sea” of chemically similar self-ligands, and this should be done very quickly to avoid pathogens affecting the organisms. In other words, the successful functioning of the T cells must be simultaneously characterized by high degrees of sensitivity, specificity, and speed (3, 4, 5). In recent years, substantial progress has been made in understanding the mechanisms of activation of the adaptive immune systems and specifically for T cell signaling (2,6, 7, 8, 9, 10, 11, 12, 13, 14, 15). However, the molecular picture of how the absolute discrimination of self-ligands versus non-self-ligands is achieved remains not well understood. Originally, the affinity model, which assumes that T cell activation is proportional to the probability of forming TCR-pMHC complexes, has been proposed (16, 17, 18, 19, 20). The key prediction of this model is that the activation is a function of TCR-ligand equilibrium affinity. But weak correlations between the activation and the TCR-ligand affinity have been found experimentally (7,17), essentially invalidating this model. The currently dominating view on T cell activation is based on a kinetic proofreading (KPR) model and its modifications (2,21,22). It assumes that after the binding of TCR to pMHC, several sequential phosphorylation events are taking place before the final fully phosphorylated state capable of activating the immune response is achieved. This leads to a delay between ligand binding and T cell signaling. This observation stimulated a lifetime binding concept that there is a threshold in the binding times that separates two types of ligands (7,23, 24, 25, 26). According to this idea, T cells do not respond to fast binders (less than ∼3–5 s), but they respond to ligands with longer association times. The subject remains controversial, with several alternative ideas having been proposed and discussed (10, 11, 12,27). Recent experimental studies using optogenetics techniques, however, indicated support for kinetic proofreading as a regulatory mechanism for the activation of the T cell receptor (28,29), but the molecular details of the underlying processes are still not well understood.

Although the binding lifetime was found to be a good predictor for activation of T cells in some situations, in many systems it did not correlate well with the correct activation events (7,17). The strongest challenge to the lifetime binding concept comes from recent experimental measurements on interactions between T cell receptors and peptide-MHC ligands (7,17). It was found that for fast-binding peptides, the lifetime failed to correctly predict the activation. In these cases, the binding lifetimes were short, but the activation still took place. To explain these observations, it was argued that because of the fast on rates, there are multiple rebindings that effectively increase the overall association lifetime (7). However, there are several issues with these arguments. They assume a slow signaling deactivation in the system, which contradicts the kinetic proofreading mechanism. In addition, it was shown from experimental observations that only one or two rebindings might happen, and even assuming an effective increase in the association times, the overall correlations between the aggregate binding lifetimes and T cell activation improve slightly. Furthermore, the molecular origin of the binding lifetime being the criterion for activation remains unexplained.

Here, we propose a, to our knowledge, new hypothesis on the potential origin of the absolute discrimination in T cells. We argue that the decision to activate or not to activate the immune response is governed by the characteristic timescales to form the active TCR-ligand complex that transfers the signal to the corresponding downstream biochemical networks. The idea is developed in terms of a discrete-state stochastic model for T cell signaling that adopts a single-molecule view of the antigen discrimination process. It allows us to explicitly evaluate all relevant properties of the activation process. The hypothesis is tested then with experimental data in which the T cell response is characterized by a half-maximal effective concentration (EC₅₀), also known as a ligand potency. A clear separation of triggering the immune response for foreign ligands versus no signal for the self-ligands as a function of the relaxation times is observed, supporting our theoretical predictions. The theoretical framework also provides a comprehensive description of sensitivity, selectivity, and speed of T cell activation, which are the main characteristics of the antigen discrimination process. This allows us to discuss the range of parameters at which the most optimal behavior of immune response activation might be achieved. In addition, it is found that the level of stochastic noise differs for self-peptide and for foreign peptides, which might provide an additional mechanism to achieve absolute discrimination in T cell functioning.

Methods

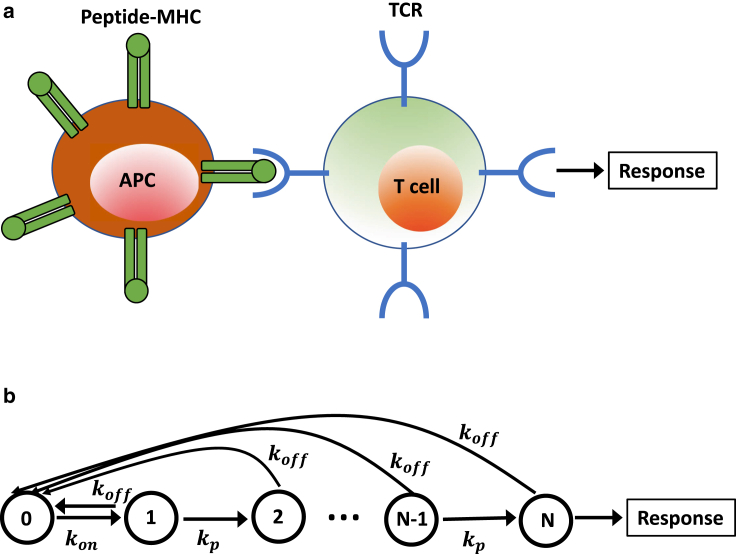
Because of the recent experimental support for the KPR model (28,29), in our theoretical approach, we consider a discrete-state stochastic model of T cell activation as shown in Fig. 1 (22). A similar model has been considered in (30), in which the mean first passage times for the completion of biochemical processes were calculated. Our model is slightly simpler, but it allows us to calculate the relaxation dynamics to the stationary behavior, which has not been done before. We argue that this might be crucial for understanding the molecular mechanisms of T cell activation. There are N states of association between TCR and pMCH that we label as states n for n = 1, 2,…, N. They correspond to the bound conformations with different degrees of phosphorylation. The state n = 0 describes the ligand and receptor being dissociated from each other. We assume that the state n = N, which is the final phosphorylated state, is the signaling state that starts the biochemical processes that lead to T cell activation. The original TCR-pMHC complex (state n = 1) forms with a rate k_on, and any of the bound conformations (states n = 1, 2,…, N) can dissociate to the state n = 0 with a rate k_off (see Fig. 1). It is important to clarify here that the effective binding rate k_on is a product of the corresponding kinetic rate constant (in units of 1/s) and the concentration of the antigen-presenting cells (in units of M). But the rebinding of TCR and pMHC always lead to the state n = 1. The phosphorylation events change the state n to the state n + 1 (for n = 1, 2,…, N − 1) with a rate k_p. This is a very simplified biochemical scheme that is believed to be capturing some of the relevant processes taking place during the interactions between the T cell and peptide ligands. Note that the TCR signaling transduction itself is a very complex biochemical process that involves multiple proteins, such as LCK, ZAP70, and LAT, which recruit multiple effector and adaptor molecules (15).

Figure 1.

(a) A schematic description of the activation of a T cell during the immune response. A T cell binds via a TCR to an antigen-presenting cell. If a foreign peptide is identified, the response is activated. (b) shows a schematic view of the simplest kinetic proofreading model for the antigen discrimination. Each state n (1 ≤ n ≤ N) corresponds to a complex between TCR and pMHC with different degrees of phosphorylation. State n = 0 describes the unbound TCR and pMHC species. The immune response is activated when the system reaches the state n = N and the stationary concentration of this state is achieved. To see this figure in color, go online.

To simplify calculations, we adopt a single-molecule view of the process, i.e., the interaction between one TCR and one pMHC molecules are considered; however, actual concentrations of participating cellular species are easily recovered. Let us define a function P_n(t) as the probability to reach the state n at time t. At t = 0, the system starts in the unbounded state n = 0. The time evolutions of these probabilities are governed by following master equations:

$$\frac{d{P}_0\left(t\right)}{dt}=k_{off}\sum _{n=1}^N{P}_n\left(t\right)-k_{on}{P}_0\left(t\right),$$ (1)

for n = 0,

$$\frac{d{P}_1\left(t\right)}{dt}=k_{on}{P}_0\left(t\right)-\left(k_p+k_{off}\right)P_1\left(t\right),$$ (2)

for n = 1,

$$\frac{d{P}_n\left(t\right)}{dt}=k_p{P}_{n-1}\left(t\right)-\left(k_p+k_{off}\right)P_n\left(t\right),$$ (3)

for 1 < n < N, and

$$\frac{d{P}_N\left(t\right)}{dt}=k_p{P}_{N-1}\left(t\right)-k_{off}{P}_N\left(t\right),$$ (4)

for n = N. We note that the probability functions are subject to normalization condition, ${\sum }_{n=0}^N{P}_n\left(t\right)=1$. As shown in the Supporting Materials and Methods, the stationary probability for the complex to be in the state N can be found from master equations when the left sides of these equations are set to be equal to zero, yielding

$$P_N=\frac{k_{on}}{\left(k_{on}+k_{off}\right)}{\left(\frac{k_p}{k_p+k_{off}}\right)}^{N-1}$$ (5)

This expression has a very clear physical meaning. The first factor, $\left(k_{on}/\left(k_{on}+k_{off}\right)\right)$, is the probability of forming a TCR-pMHC complex in any phosphorylation state, whereas the second factor, ${\left(k_p/k_p+k_{off}\right)}^{N-1}$, gives the probability of being in the final activation state after N − 1 sequential phosphorylations (31). Therefore, P_N gives the fraction of TCR-ligand fully phosphorylated complexes.

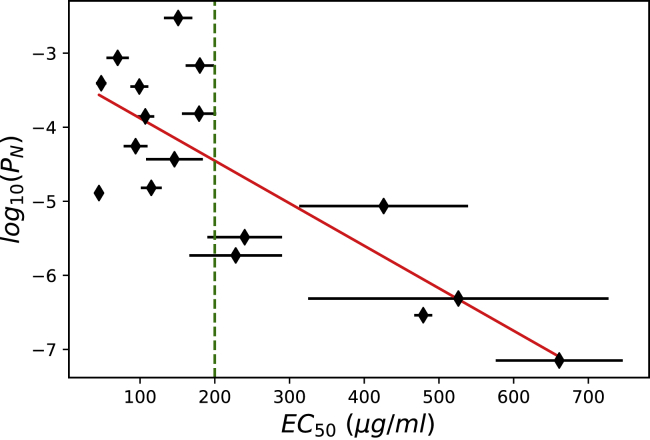
In our theoretical approach, we assume that the T cell makes the decision to activate when the system reaches the final phosphorylated state (n = N in Fig. 1) at the stationary-state level. Thus, the function P_N can be regarded as a triggering probability such that the higher values of P_N correspond to the higher probability of activation. This can be tested using the experimental data as shown in Fig. 2. Using the kinetic parameters and ligand potency associated with different mutants of the peptide NY-ESO-1_157–165(ESO-9C) interacting with 1G4 TCR (32) and taking a reasonable choice for other parameters such as the number of phosphorylation steps and the phosphorylation rate (9), one can estimate P_N for different peptides and compare them with the EC₅₀, or ligand potency. EC₅₀ is a concentration of the ligand that induces the activation of T cells in $50\text{\%}$ of cases. Thus, the lower values of EC₅₀ describe strong activation, whereas the higher values of EC₅₀ correspond to a weak activation response. Fig. 2 shows that T cell activation correlates with the probability of finding the system in the final phosphorylated state n = N, and this clearly supports our theoretical arguments. Although the correlation is not perfect (R² = 0.64), it should be noticed that experimentally measured EC₅₀-values have large error bars (see Fig. 2) due to a variety of reasons, including fluctuations in the concentrations of participating molecules and variability in the measuring procedures.

Figure 2.

Correlations between the stationary-state probability function P_N and the ligand potency EC₅₀ represented by the concentration stimulating half-maximal IFN_γ secretion. Regression analysis yields a coefficient of correlation R² equal to 0.64 and a p-value of 1.2 × 10⁻⁴. The ligand potency EC₅₀ and kinetic parameters k_on and k_off used to evaluate P_N are taken from (32). Corresponding error bars are shown for EC₅₀. A vertical dashed line separates the data into two different groups: self-peptides (large EC₅₀) and foreign peptides (small EC₅₀). In calculations, N = 6 and k_p = 0.1 s⁻¹ were utilized as suggested in (9) and (22). To see this figure in color, go online.

Having argued that the fully phosphorylated conformation of the TCR-pMHC complex is most probably responsible for the activation of the immune response, we propose that the discrimination between self-ligands and foreign peptides is controlled by the time to reach the stationary level of this conformational state. This timescale, which is also known as a local relaxation time, is defined as a time to achieve the stationary probability P_N in the state n = N if the system started in the state n = 0 (unbound TCR and pMHC molecules) originally. It can be explicitly evaluated using a theoretical method developed in (33). One could define a local relaxation function for the state n > 0,

$$R_n\left(t\right)=1-\frac{P_n\left(t\right)}{P_n^{\left(s\right)}},$$ (6)

where P_n(t) is the probability for the system to be in the state n at time t, whereas $P_n^{\left(s\right)}$ is the stationary probability to be found in this state. The physical meaning of the function R_n(t) is the relative distance to the stationary conditions in the state n at time t. For n > 0, we have R_n(t = 0) = 1 and R_n(t → ∞) = 0. It can be shown that the average time τ_n to reach the stationary concentration at the state n can be explicitly evaluated knowing the function R_n(t) (see the details of calculations in the Supporting Materials and Methods). For the fully phosphorylated complex n = N, we obtain

$${\tau }_N=\frac{N-1}{k_p+k_{off}}+\frac{1}{k_{on}+k_{off}}$$ (7)

In this expression, the first term describes the time to go from the state n = 1 to the final state n = N via N − 1 irreversible phosphorylation events, whereas the second term is the time responsible for establishing the stationary conditions between the unbound and bound conformations in the system. It is important to highlight the difference between the relaxation times and the binding times. The latter describe the times for the system to be found in any intermediate phosphorylation state, even in those that do not activate the response. The relaxation times, however, describe the times to reach the final biochemical state at the stationary level. The difference is important because the signal can be transferred for downstream activation of the immune response only in this biochemical state. Thus, our main idea is that for the ligands with the relaxation time to the final signaling state less than some threshold time t₀, the activation does not happen, whereas for τ_N > t₀, the immune response is activated. Experimental data suggest that this threshold timescale is of the order of t₀ ∼2–5 s (7,17,32).

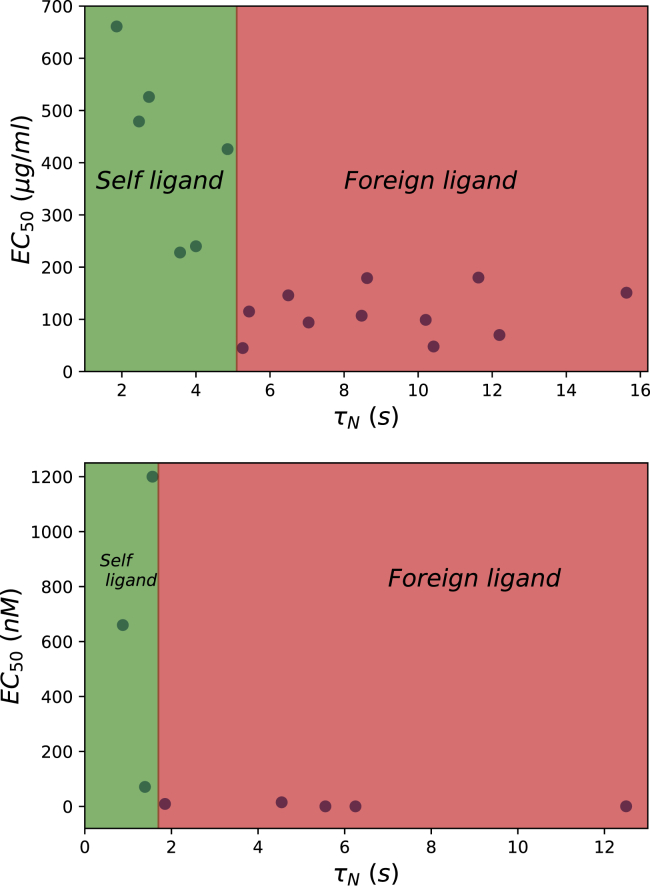
Now, we can test our hypothesis that the magnitude of the relaxation time τ_N is the criterion for T cell activation with experimental data. Once again using the results for the peptide NY-ESO-1_157–165 interacting with 1G4 TCR (32), we present the relaxation times and the ligand potency for different T cell receptors in Fig. 3 (top). One can see that data can be clearly separated into two different groups. For τ_N < 5 s, the value of EC₅₀ is large, indicating that the probability of activating the immune response is low. But the situation is different for τ_N > 5 s; here, the value of EC₅₀ is small, and the system should be activated for these peptides. Similar observations are found for a different experimental system of CD4 T cells as presented in Fig. 3 (bottom). Again, the T cell activation is governed by the relaxation times. In this system, the self-ligands have τ_N < t₀, whereas the foreign peptides exhibit τ_N > t₀ with t₀ ∼2 s. These results generally support our hypothesis on the existence of the threshold time for the specific systems in Fig. 3 that divides the relaxation times for the self-peptides (short times) and for the foreign ligands (long times) and determines the activation outcome.

Figure 3.

The relations between the relaxation times (τ_N) and the ligand potency (EC₅₀). The kinetic parameters k_on and k_off and the ligand potency EC₅₀ used to evaluate τ_N are taken from (32) (for the top plot) and from (7) (for the bottom plot). To see this figure in color, go online.

Because the T cell activation is determined by a series of biochemical processes, it raises a question on the level of stochastic noise in the system and how it might affect the activation of the immune response. Our theoretical method allows for exact analytical calculations for all dynamic properties in the system, and we can try to answer this question explicitly. To do this, we note that the relaxation times correlate with the mean first passage times to reach the final signaling state, which is given by the first term in Eq. 7. Because the calculations for the variance of the relaxation times are tedious, we performed our analysis for the variance of the mean first passage times as a quantitative measure of fluctuations and noise in the activation of T cells. In our approach, the degree of stochastic noise in T cell activation is given by the deviation from the mean first passage times. The larger the variance is, the larger is the noise in the system. As shown in the Supporting Materials and Methods, it is given by a simple expression,

$${\sigma }_{T_1}\equiv \sqrt{\langle T_1^2\rangle -{\langle T_1\rangle }^2}=\frac{\sqrt{N-1}}{k_{off}+k_p}$$ (8)

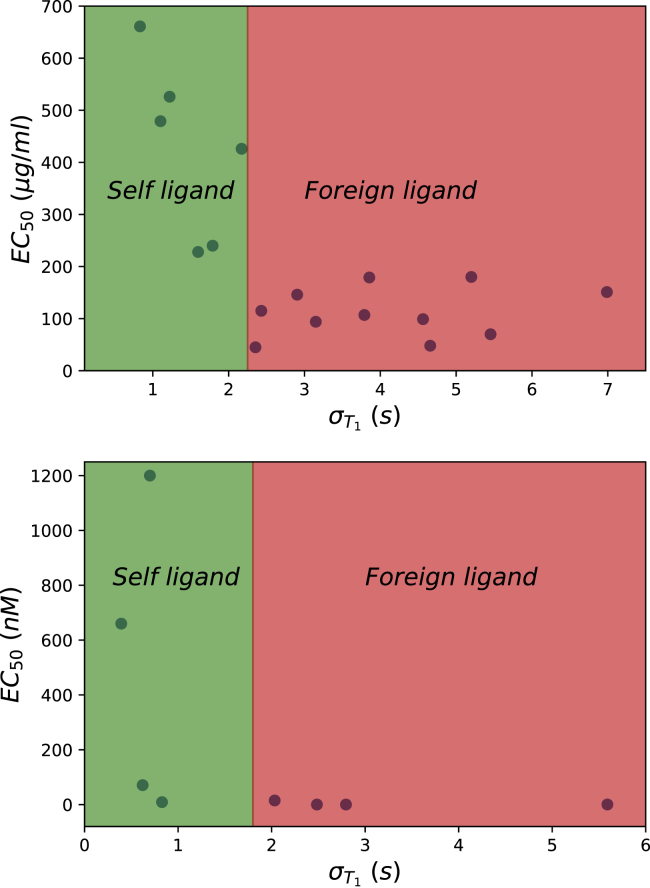
Fig. 4 presents the variance of mean first passage times and the ligand potency for different T cell receptors using experimental data. Interestingly, it is found that the degree of stochastic noise differs for various species. It seems that for self-peptides, the system quickly reaches the final active biochemical state, producing not much noise. For foreign peptides, however, it takes longer to approach the final active biochemical state, and this leads to a larger noise. Thus, one can see that larger noise is observed for foreign peptides, whereas smaller noise is predicted for the self-peptides. It is unclear at this moment if the separation based on the different level of stochastic noise might be also utilized as an additional mechanism of activation, but it will be intriguing to explore such possibility in the future.

Figure 4.

The relations between the variance of the mean first passage times $\left({\sigma }_{T_1}\right)$ and the ligand potency (EC₅₀). The kinetic parameters k_on and k_off and the ligand potency EC₅₀ used to evaluate τ_N are taken from (32) (for the top plot) and from (7) (for the bottom plot). These data are also presented in the Supporting Materials and Methods. In calculations, N = 6 and k_p = 0.1 s⁻¹ were utilized as suggested in (9) and (22). To see this figure in color, go online.

These data are also presented in the Supporting Materials and Methods. In calculations, N = 6 and k_p = 0.1 s⁻¹ were utilized as suggested in (9) and (22).

Our theoretical approach also allows us to quantify the most important characteristics of the T cell activation process, namely speed, sensitivity, and selectivity, and the relations between them. It has been argued that the successful functioning of the immune system requires that all three properties to be in a specific range of parameters, which is called a “golden triangle” (6). It is known that the T cells spend limited time in the vicinity of the antigen-presenting cells (34, 35, 36, 37). This requires that the T cells must act quickly to recognize and to respond to the foreign ligands. Stimulated by our theoretical hypothesis on the importance of the relaxation times, we naturally define the speed of T cell signaling as the inverse of the time to reach the stationary concentration of the TCR-ligand-activated complex,

$$\text{Speed}=\frac{1}{{\tau }_N}=\frac{\left(k_{on}+k_{off}\right)\left(k_{off}+k_p\right)}{k_p+k_{off}+\left(N-1\right)\left(k_{off}+k_{on}\right)}$$ (9)

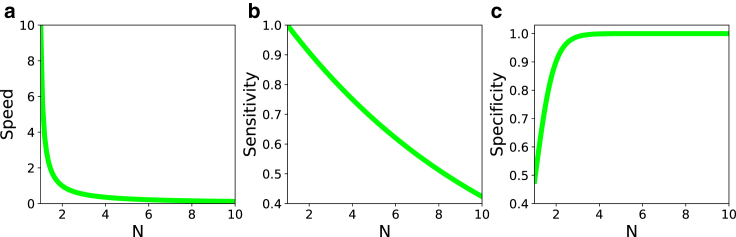
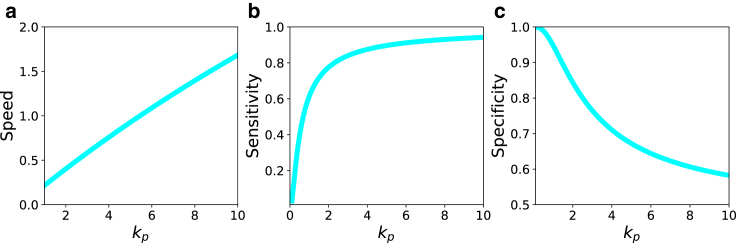
Using realistic values of the transition rates, we plot the dependence of the T cell activation speed on the number of phosphorylation steps in Fig. 5 a and on the phosphorylation rate in Fig. 6 a. Increasing the number of intermediate phosphorylation steps dramatically lowers the speed of activation (Fig. 5 a). This is the expected result because it takes longer times for the system to reach the final signaling state n = N after the initial binding of TCR to pMHC (state n = 1). The trend is opposite for varying the phosphorylation rate (Fig. 6 a). Increasing k_p accelerates the speed of the T cell activation because the system can now reach the final state n = N faster (see Eq. 7). However, the effect of varying the phosphorylation rate is generally weaker than changing the number of the intermediate steps in the KPR model, suggesting that for real systems the number of phosphorylation events cannot be large.

Figure 5.

The dependence of speed, specificity, and selectivity of T cell activation on the number of phosphorylation steps. (a) shows the speed for k_p = 1 s⁻¹, k_off = 0.10 × k_p, and k_on = 10 s⁻¹; (b) shows the sensitivity for k_p = 1 s⁻¹, k_off = 0.10 × k_p, and k_on = 100 s⁻¹; and (c) shows the specificity for k_p = 1 s⁻¹, $k_{off}^{\left(\text{foreign}\right)}$ = 0.10 × k_p, $k_{off}^{\left(\text{self}\right)}$ = 10 × k_p, $k_{on}^{\left(\text{foreign}\right)}$ = 1 s⁻¹, and $k_{on}^{\left(\text{self}\right)}$ = 1000 s⁻¹. To see this figure in color, go online.

Figure 6.

The dependence of speed, specificity, and selectivity on the phosphorylation rate k_p (in s⁻¹). (a) shows the speed for N = 6, k_off = 0.10 s⁻¹, and k_on = 10 s⁻¹; (b) shows the sensitivity for N = 6, k_off = 0.10 s⁻¹, and k_on = 10 s⁻¹; and (c) shows the specificity for N = 6, $k_{off}^{\left(\text{foreign}\right)}$ = 0.1 s⁻¹, $k_{off}^{\left(\text{self}\right)}$ = 1 s⁻¹, $k_{on}^{\left(\text{foreign}\right)}$ = 1 s⁻¹, and $k_{on}^{\left(\text{self}\right)}$ = 1000 s⁻¹. To see this figure in color, go online.

The second major characteristics of the T cell response is sensitivity. It has been shown that T cells recognize and respond to a very small amount of pathogen-derived ligands on antigen-presenting cells (5,38). Sensitivity can be viewed as the probability of achieving a state when T cell activation starts (39). In our formalism, this is equivalent to the probability of the stationary concentration for the fully modified TCR-ligand complex,

$$\text{Sensitivity}=P_N=\frac{k_{on}}{\left(k_{on}+k_{off}\right)}{\left(\frac{k_p}{k_p+k_{off}}\right)}^{N-1}$$ (10)

In Figs. 5 b and 6 b, we present the effect of varying the number of intermediate states and the phosphorylation rate on the sensitivity, respectively. Our calculations suggest that the sensitivity is lower for larger number of phosphorylation events (Fig. 5 b), whereas it strongly increases and then saturates with increasing the phosphorylation rate k_p (Fig. 6 b). These results can be easily explained using the KPR model in Fig. 1. Increasing the number of intermediate steps lowers the probability of reaching the final state that starts the immune response. At the same time, increasing the phosphorylation rate drives the system in the direction of the final state n = N, and this should increase the sensitivity.

Specificity is the third important property of the T cell activation. Experiments suggest that even if self-ligands are presented in concentrations as high as 10⁵ times more than the foreign ligands, the T cells are able to respond only to the foreign peptides. Following the definition presented in (39), the specificity is defined as the probability that the T cells produced signal is correct. Given that the TCR is exposed to specific and nonspecific ligands in live cells, the specificity can be quantified as

$$\text{Specificity}=\frac{P_N^{\left(\text{foreign}\right)}}{P_N^{\left(\text{foreign}\right)}+P_N^{\left(\text{self}\right)}}$$ (11)

In this expression, $P_N^{\left(\text{foreign}\right)}$ and $P_N^{\left(\text{self}\right)}$ are the probabilities to reach the final signaling state for the foreign and self-ligand, respectively, for independent interactions events between TCR and pMHC molecules. In this definition, the specificity varies between 0 (low specificity) and 1 (high specificity). Figs. 5 c and 6 c show how the specificity varies with the number of phosphorylation steps and the phosphorylation rate, respectively. Increasing N makes T cell activation very specific. This is because at each state n > 0, self-ligands dissociate faster from the complex, and this lowers the probability of reaching the final signaling state n = N. The effect is stronger with larger N, and this improves the specificity (Fig. 5 c). But increasing the phosphorylation rate lowers the specificity (Fig. 6 c). In this case, both self-ligands and foreign ligands are quickly driven into the final signaling state, and there is no time for discrimination between different peptides. This result explains recent observations on tyrosine phosphorylation of the T cell adaptor protein LAT at position Y132 (40). In these experiments, the mutations that lead to faster phosphorylation kinetics have negative consequences for ligand discrimination. Our theoretical approach is able to explain this surprising result from the molecular point of view.

The quantitative analysis of the speed, sensitivity, and specificity of the T cell activation presented in Figs. 5 and 6 gives a specific information on the parameters range that support the most efficient functioning of immune system. We suggest that the “golden triangle” can be realized for intermediate values of the number of phosphorylation steps and not too small and not too large values of the phosphorylation rates. However, more molecular-level information on the underlying biochemical and biophysical processes during the immune response are needed to be more specific.

Discussion

In this article, we propose a new criterion for absolute ligand discrimination in T cells activation. It argues that the relaxation time of forming the stationary concentrations of the final signaling complexes between TCR and pMHC governs the activation of the immune response. When these relaxation times are shorter than some threshold value, the signal is not activated, whereas for longer relaxation times, the response is activated. The available experimental data generally support this picture. But it is important to emphasize the differences between our, to our knowledge, new approach and the current views on the mechanisms of immune response. The novelty of our work is that we propose a new criterion of T cell activation that might help to better clarify the underlying molecular mechanisms. We note that our hypothesis does not fully contradict the existing concept of binding lifetimes being the decisive factors in the activation. This is because in many situations, the relaxation times and the binding lifetimes correlate with each other. But the proposed criterion also works in situations when the binding lifetime concept fails. Furthermore, arguments are presented to suggest that the level of stochastic noise might be an additional factor in achieving the absolute discrimination. Thus, the hypothesis generalizes the existing views, and it allows us to resolve contradictory experimental observations.

We note that the KPR model has been widely utilized in theoretical and experimental studies on the immune response activation (9,12,22). There are two main advances of our theoretical method. First, it explicitly evaluates the relaxation times to reach the stationary states, and this was not previously accomplished. The second most important contribution is the hypothesis that the relaxation times determine whether T cell activation starts or not. It is also crucial to emphasize that even if future studies will prove that a more complex biochemical description is needed to describe the immune response activation, our idea that the timescale of reaching the stationary conditions is the criterion for activation will still be valid.

One of the additional advantages of our theoretical method is the ability to comprehensively describe the major properties of T cell activation such as speed, sensitivity, and specificity. Exact analytical expressions for all these properties are presented, allowing us to analyze the intrinsic relations between them. It is shown explicitly that the specific biochemical conditions might be optimized to effectively activate the T cell response in the most efficient way. This would explain how the immune response in biological systems can be simultaneously fast, sensitive, and specific. This allows us to speculate more on the possible ranges of parameters in the system that might satisfy the “golden triangle” requirements. It will also be important in the future to investigate the energy dissipation and other properties of T cell activation to test whether other features of the immune response can be optimized in the similar fashion (41,42).

The proposed criterion that the relaxation times control the switching of the immune response agrees reasonably well with experimental observations, but it does not provide a molecular picture on the mechanisms of absolute discrimination or on the molecular origin of the threshold that separate self-ligands and foreign pathogens. The full details of downstream biochemical processes that are taking place in the immune response are still not well understood (15). For this reason, multiple mechanisms consistent with the relaxation time criterion might be proposed. To stimulate more discussions on this important topic, let us suggest a very speculative possible molecular mechanism. One might suggest that “any” binding of TCR to pMHC activates a specific downstream biochemical cascade related to the cellular immune response. If the system reaches the final phosphorylation state (at the stationary-state level when the signal can be reliably produced) faster than the completion of the first biochemical cascade activated after the binding, then the second biochemical cascade starts. We postulate that when both biochemical cascades act together, they do not lead to the activation of the immune response. However, if the final signaling state is reached later than the first cascade is completed, the immune response starts because of the action of only the first biochemical cascade. This picture provides a possible explanation for the appearance of the threshold and its relationship with the relaxation times. But the details of the proposed mechanism are still too coarse grained and not well defined. It will be important to get more molecular information on the processes governing T cell activation.

Although the presented theoretical approach is able to provide a consistent description of the activation processes in T cells, it should be emphasized that the model is very simplified with multiple assumptions that need to be fully explored, and it also neglects some important features of the process. For example, it is realistic to expect a more complex biochemical network description of the interactions between TCR and pMHC (12,15). More specifically, the phosphorylation steps are reversible, although taking this effect into account should not modify our main predictions; the phosphorylation rate and dissociation rates might be conformational-state dependent; and the system might have multiple feedback loops. The explicit calculations for such more general models are possible. Furthermore, our method completely neglects the role of the cellular membranes where TCR are located, the cell-cell communications, and the cell topography during these interactions. These aspects might be important for the activation of immune response. However, despite these issues, our method provides a simple quantitative theoretical description of TCR triggering, which is based on fundamental physical-chemical principles. Another advantage of our approach is that it gives experimentally testable predictions on major properties of the T cells’ activation. This should clarify the molecular picture of the immune response in biological systems and stimulate more experimental investigations.

Author Contributions

H.T. and A.B.K. designed the research. H.T. and A.B.K. carried out all calculations. H.T. analyzed the data. H.T. and A.B.K. wrote the article.

Editor: Stanislav Shvartsman.