Figure 5: Illustration of a normally hyperbolic and invariant critical manifold, $\mathcal{M}$.

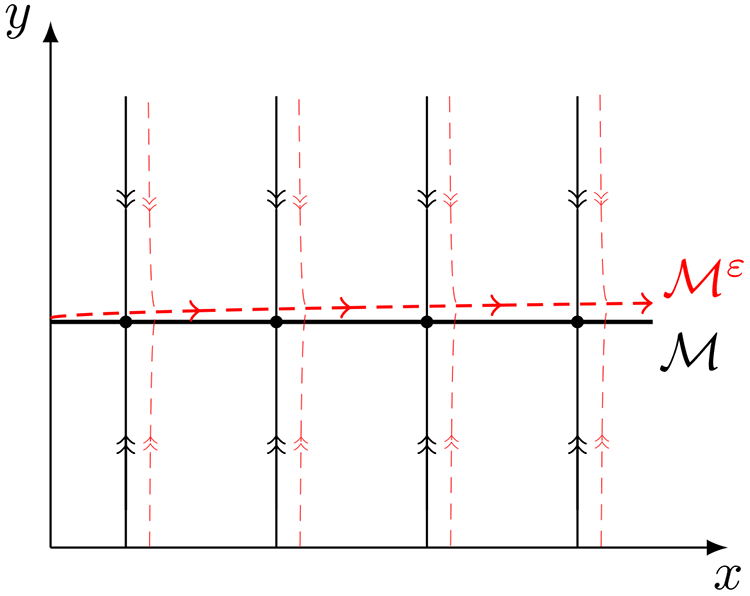
The black lines with arrows and fixed points represent trajectories within the unperturbed vector field field; the red dashed lines represent trajectories in the perturbed vector field. The straight black lines with double arrowheads represent trajectories moving towards the fixed points (filled black circles) that lie on the normally hyperbolic, attracting and invariant manifold $\mathcal{M}$, depicted by the thick black line. The flow on $\mathcal{M}$ is trivial. However, once ε is non-zero and the vector field is smoothly perturbed, an invariant manifold ${\mathcal{M}}^{\epsilon }$ emerges (red), on which the flow is slow, but no longer trivial. Trajectories that start off of ${\mathcal{M}}^{\epsilon }$ quickly approach it, then follow it tangentially. Obviously, the fixed points drawn on this manifold are isolated, so the reader should bear in mind that $\mathcal{M}$ is filled with non-isolated fixed points.