Figure 6: The transcritical bifurcation point corresponds to a loss of normal hyperbolicity and an exchange of stability.

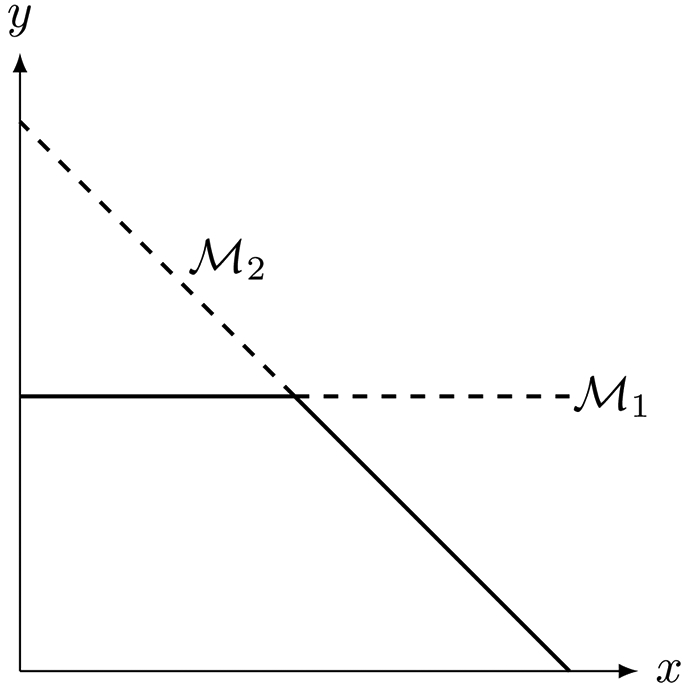
Here we illustrate a transcritical bifurcation. Thick dashed lines corresponds to unstable fixed points in which (58) is greater than zero. Thick solid lines represent stable branches of fixed points for which (58) is negative. Two manifolds, ${\mathcal{M}}_1$ and ${\mathcal{M}}_2$, cross at a singular point. At the crossing point (i.e, the point of intersection), normal hyperbolicity is lost, and (58) fails to hold. Each manifold undergoes a change in stability at the point of intersection (i.e., the singular point delimits the point at which the stability of each of the manifolds changes from attractive to repulsive or vice-versa).