Figure 8: The critical set of the rQSSA when e₀ < s₀ and K_M = 0.

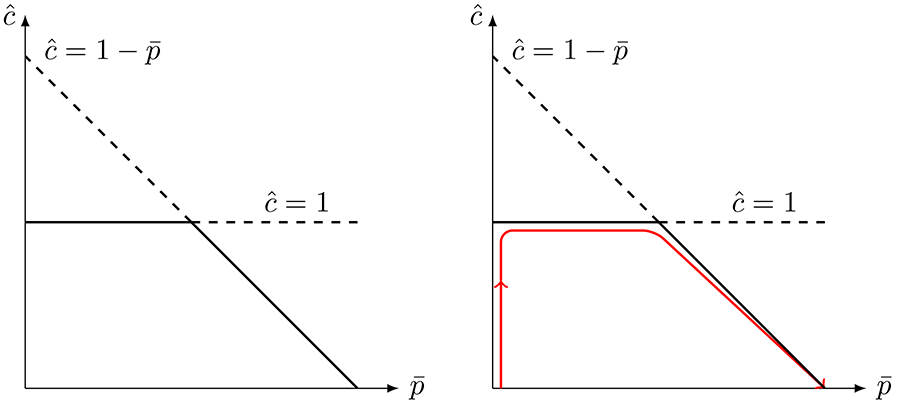
This figure provides a visualization of the invariant set recovered by setting e₀ < s₀ and k₋₁ = k₂ =0. Left: The critical set contains two transversely intersecting branches of fixed points. Thick solid curves correspond to non-isolated stable fixed points, and thick dashed lines correspond to unstable fixed points. The horizontal curve corresponds to the critical set $\widehat{c}=1$, and the diagonal curve corresponds to the critical set $\overline{p}+\widehat{c}=1$. The trajectory rapidly approaches the curve $\widehat{c}=1$, then reaches the curve $1=\widehat{c}+\overline{p}$ once t ~ t_ℓ, and begins descending towards the origin. Clearly, each set constitutes a normally hyperbolic manifold everywhere except where the branches intersect, which corresponds to a transcritical singularity. Right: A typical trajectory (red solid curve) closely follows the attracting critical submanifolds once the perturbation is turned on.