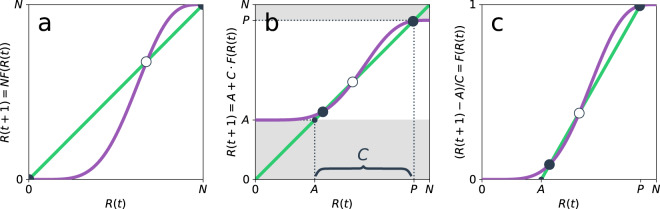
Figure 1.
Extension of Granovetter’s (graphic) model with P potentially and A certainly acting individuals. (a) The original model that computes the number of acting individuals from the cumulative distribution function of thresholds . The purple line indicates a typical normal-like choice for this distribution. The 45°-line (green) intersects at the stable (black) and unstable (white) equilibrium points R*. As for many realistic choices of , only R* = 0 and R* = N are stable. (b) Introducing A certainly and P potentially acting individuals, such that the contingent individuals have the same threshold distribution as the entire population . Here, the equilibria move to the interval and are not necessarily located at exactly and . Hence, the certainly acting individuals trigger some contingent individuals to act, too. (c) Rescaling to the unit interval shows that equilibria can be computed by shifting the diagonal line from crossing and (as in (a)) to crossing and and using the same threshold distribution F as in (a).