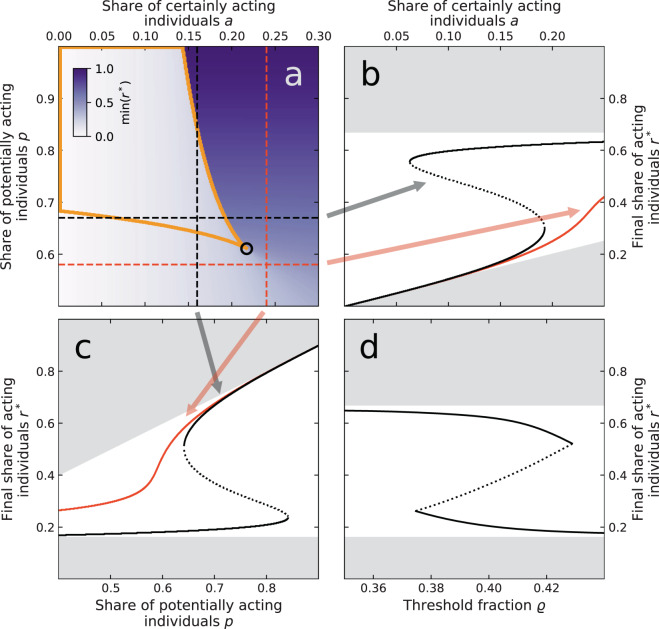
Figure 4.

Bifurcation analysis and hysteresis of the refined Granovetter model with an emergent threshold distribution as given by the analytical approximation. (a) Smallest stable fixed point min(r*) for different shares of certainly acting $a$ and potentially acting individuals $p$. The black circle denotes a cusp-bifurcation. Black dashed horizontal/vertical lines correspond to the diagrams in (b,c) that show a saddle-node bifurcation. For (b–d), solid (dotted) lines indicate stable (unstable) fixed points r*. Grey shading indicates those areas where $r^{⁎}\notin [a,p]$ and that can thus not be reached. The yellow circled area in (a) indicates the bistable regime. Red dashed horizontal/vertical lines in (a) correspond to values of p and a at which no bifurcation is observed and thus r* varies smoothly in (b,c). (d) Shows the bifurcation diagram in the threshold fraction $\rho$. Fixed parameters are: $a=0.16$ for (c) ($a=0.24$ for the red curve) and (d), $p=0.67$ for (b) ($p=0.58$ for the red curve) and (d), and $\rho =0.4$ for (a–c).