An evaluation of COVID-19 in Italy: A data-driven modeling analysis

Abstract

The novel coronavirus (COVID-19) that has been spreading worldwide since December 2019 has sickened millions of people, lock down major cities and some countries, prompted unprecedented global travel restrictions. Real data-driven modeling is an effort to help evaluate and curb the spread of the novel virus. Lockdowns and the effectiveness of reduction in the contacts in Italy has been measured via our modified model, with the addition of auxiliary and state variables that represent, contacts with infected, conversion rate and latent propagation. Results show the decrease in infected people due to stay-at-home orders and tracing quarantine intervention. The effect of quarantine and centralized medical treatment was also measured through numerical modeling analysis.

1. Introduction

In December 2019, an unprecedented outbreak of pneumonia with an unknown cause occurred in Wuhan, capital of Hubei province in central China. A novel coronavirus was identified as a pathogen, which named covid-19 by the World Health Organization (WHO) subsequently (W. H. Organization, 2020). It spans a long incubation period and has highly infection among human beings (Tu, Tu, & Gao, 2020). Currently, the confirmed cases of COVID-19 are up to 8,708,008 and 461,715 fatality cases occurred in global as of June 21. The heavy shock has burdened more than SARS and Middle East Respiratory Syndrome (MERS), which happened in 2003 and 2013, respectively. Under the strict large-scale prevention and control mechanism, new cases of COVID-19 have decreased rapidly in China. But 2,527,618 cases still occurred in Europe and 4,279,854 in Americas as of June 21. The new cases are on the up road, which brings severe challenge to health security in the world. (see Table 1)

Table 1.

The description and initial setting of variables and parameters.

Variables	Setting	Explanations
S	60482200	Italy’s population as of March 2020.
E	17831	The difference between the number of diagnosed cases on March 10 and March 16, 2020.
I	8514∗1.5	The undetected number on March 10.
$S_q$	2936	Number of patients who tested positive for nucleic acid on 10 March but underwent isolation without symptomatic manifestations.
$E_q$	423	Less than $S_q$.
H	13194	Less than $I+E_q$.
R	1004	Official data.
Parameter	The value	Explanations	95% CI for model error
c	2.6	According to lockdown time.	[0.048, 0.070]
${\delta }_I$	0.02	Real data’s estimation.	[0.145, 0.219]
${\delta }_q$	0.1259	Literature (Wang et al., 2020).	[0.815, 2.119]
${\gamma }_I$	0.0082	Deduced form real data.	[0.147, 0.148]
${\gamma }_H$	0.006	Deduced form real data.	[0.045, 0.473]
β	$2.05\text{∗}{10}^{-9}$	Deduced form real data.	[0.144, 0.333]
q	$1\text{∗}{10}^{-6}$	Deduced form real data.	[0.355, 1.228]
α	0.00027	Deduced form real data.	[0.055, 0.091]

The outbreak has hit Europe, it reports more than 24,000 cases in Italy by mid March from Center for Systems Science and Engineering at Johns Hopkins University, and increased rapidly in the following days, where became the second-largest number of confirmed cases since March 20, 2020. Limited capacity of hospital care burdened the Italian health system heavily. Modeling research from Remuzzi A and Remuzzi G (Remuzzi & Remuzzi, 2020) overestimated the number cases but a severe lesson has been presented by Andrea Saglietto et al. (Saglietto et al., 2020). The effective models can describe the real data and predict the trend, such as SEIR model, what had been used to simulate the different preventing duration and different control intensity via parameters for COVID-19 epidemic in Wuhan city (Cai, 2020; (Li and Yang)). But Nicholas P. Jewell deemed that the primary and most effective use of epidemiological models is to estimate the relative effect of various interventions in reducing disease burden rather than to produce precise quantitative predictions (Jewell, 2020). In our opinion, estimates that emerge from modeling studies are not only validating to the epidemiological or statistical analysis for the real data (Giordano, Blanchini, & Bruno, 2020), but also assessing the effectiveness and efficiency of the isolation and containment measures proposed by the government, especially to the unpredictable cases, such as the presence of asymptomatic infected patients, which is a big challenge to fight against COVID-19 (Mao, Wan, He, Hu, & Chen, 2020).

It seems exponential model is not suitable to the Italian situation (Remuzzi & Remuzzi, 2020). We tried the SEIR model and modified its parameters’ system according to this country lockdown state and considered asymptomatic cases since the similar SIR model was applied in the process of interpretation to prevent and control COVID-19 in China, where provided a good mode for the controlling strategy (Zhu et al., 2020). Euler numerical calculation was employed to solve it. Real data from official website of Italy proved the effectiveness of prevention and control measures such as isolation and centralized hospital via our data-driven model.

2. Mathematical model of modified SEIR

It is well-known that COVID-19 is complicated and changes its type according to race and district difference (Peter, Lucy, Colin, & Michael, 2020), and limited to capture the feature by the classical SEIR model, which is used to modeling the infectious disease (Cao et al., 2020). Here we combine the measurement of testing, isolating and hospital care process, and then divide the total cases into several parts noted as susceptible $\left(S\right)$, exposed $\left(E\right)$, infected $\left(I\right)$, recovered $\left(R\right)$, susceptible quarantine in home (No symptoms or no critical case in home for isolation, names as $S_q)$, quarantine spreader $\left(E_q\right)$ and hospitalized patients $\left(H\right)$. The transformation relationship of the population is shown in Fig. 1.

Fig. 1.

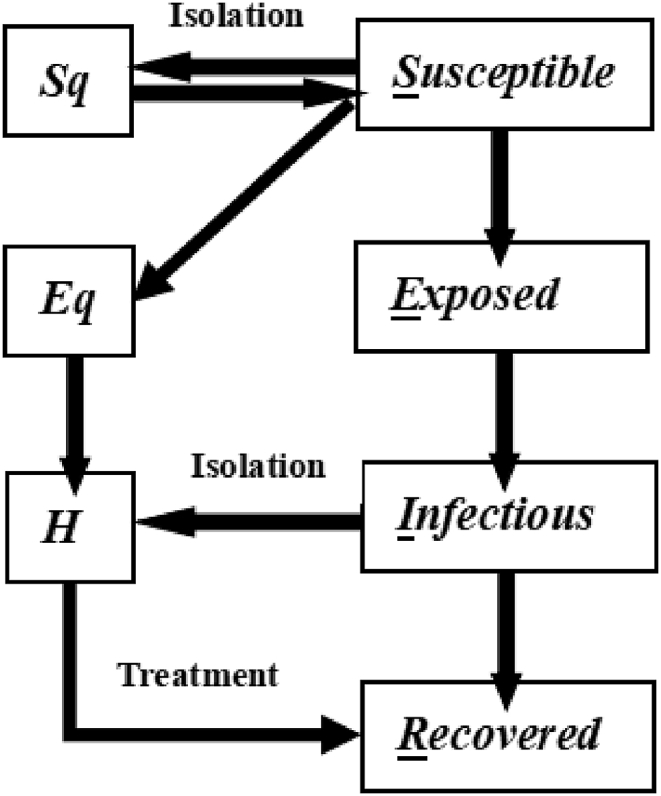
The SIER flow diagram. Flows represent per capital flows from the donor compartments.

We denoted q as the proportion of isolation, β as the probability of infection, c as the contacting rate, and ρ as the effective contact coefficient for value 1 according to the literature (Tang et al., 2019). The percent conversion from S to $Sq$, $Eq$, and E are $\rho cq\left(1-\beta \right)$ , $\rho c\beta q$ and $\rho c\beta \left(1-q\right)$ , respectively. There exists some abnormal circumstance that mild cases from the group of infected $Sq$ have been infected again, so we add the information of positive-testing cases I and ambushing cases E for the influence to susceptible group. Then the controlling function of susceptible cases is described in (1).

$$\frac{dS}{dt}=-[\rho c\beta +\rho cq\left(1-\beta \right)]S\left(I+\theta E\right)+\lambda Sq$$ (1)

where θ is the ratio of the latent to the infectious cases; Suppose that patients with latency have the same infectious capacity as those who have shown symptoms, i.e. $\theta =1$. λ is the releasing rate from isolation, we denote $\lambda =1/14$ since the isolation time was 14 days. The modified SEIR kinetic equation for covid-19 outbreak has been constructed as shown in (2).

$$\{\begin{array}{ccc}dS/dt& =& -[\rho c\beta +\rho cq\left(1-\beta \right)]S\left(I+\theta E\right)+\lambda Sq\\ dE/dt& =& \rho c\beta \left(1-q\right)S\left(I+\theta E\right)-\sigma E\\ dI/dt& =& \sigma E-\left({\delta }_I+\alpha +{\gamma }_I\right)I\\ d{S}_q/dt& =& \rho cq\left(1-\beta \right)S\left(I+\theta E\right)-\sigma S_q\\ d{E}_q/dt& =& \rho c\beta qS\left(I+\theta E\right)-{\delta }_q{E}_q\\ dH/dt& =& {\delta }_{I}I+{\delta }_q{E}_q-\left(\alpha +{\gamma }_H\right)H\\ dR/dt& =& {\gamma }_{I}I-{\gamma }_{H}I\end{array}$$ (2)

where σ is the conversion rate from the latent to infected case and $\sigma =1/14$; α is fatality rate, ${\delta }_I$ is the speed rate of isolation, ${\gamma }_I$ is the recovery rate of infection, ${\delta }_q$ is the transferring rate from the isolated lurker to isolated infectious case, and ${\gamma }_H$ is the recovered rate of infection.

Here we chose the Euler numerical method to solve the equation group (2), and the integral step is set as 0.01. According to the parameter setting in (Wang et al., 2020).and real data from Italy, the statistical siginificance of parameters is demonstrated by mean absolute percentage error(MAPE) of the fitted model, which shows the highly interpretable and reliable of our simulation.

3. Real data analysis

3.1. Data sources and model assumptions

The real data used in this article downloaded from the official website of the Italian Ministry of Health (http://www.salute.goy.it/nuovocoronavirus). At the local time on March 9, 2020, Giuseppe, the Prime Minister of Italy, held a press conference to announce the great pressure of the epidemic prevention and control, and signed an order to extend the isolated districts to the whole country. We aimed to assess quantitatively the isolation effect of this country, so the modeling-driven data started from the lockdown day of March 10.

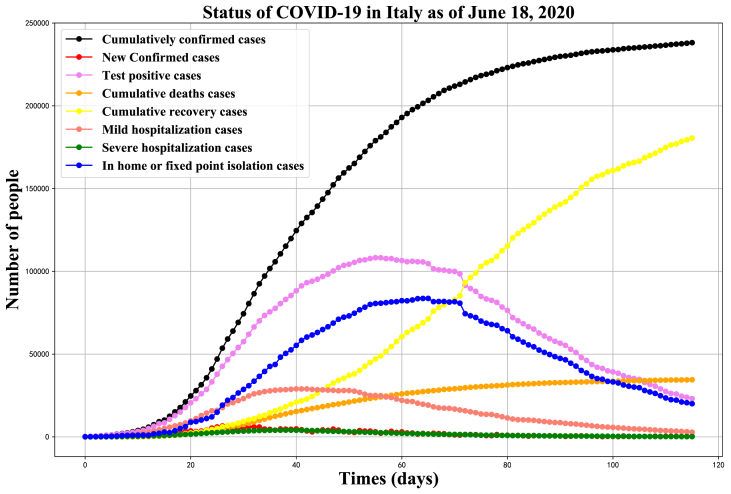
Since the first indigenous case was confirmed in the northern Italy on February 21, a red zone, was instituted in the next day, which put on lockdown to prevent the emerging threat. On March 9, The entire country was declared as red zone. It shows the infectious situation from February 24 to June 18 in Fig. 2. The inflection point of newly confirmed cases has emerged in March 21 which is the peak with 6557 increased cases and then drop down. The number of minor and severe hospitalizations has decreased after 14 days of lockdown. The increasing speed of cumulative number for confirmed cases has slowed down since April 11, which is consistent with the effect of second stage for prevention and control measures(Fig. 2).

Fig. 2.

Epidemic curves for Italy, with infectious situation from February 24 to June 18, 2020.

3.2. The infectivity of incubation on the number of confirmed and recovered cases

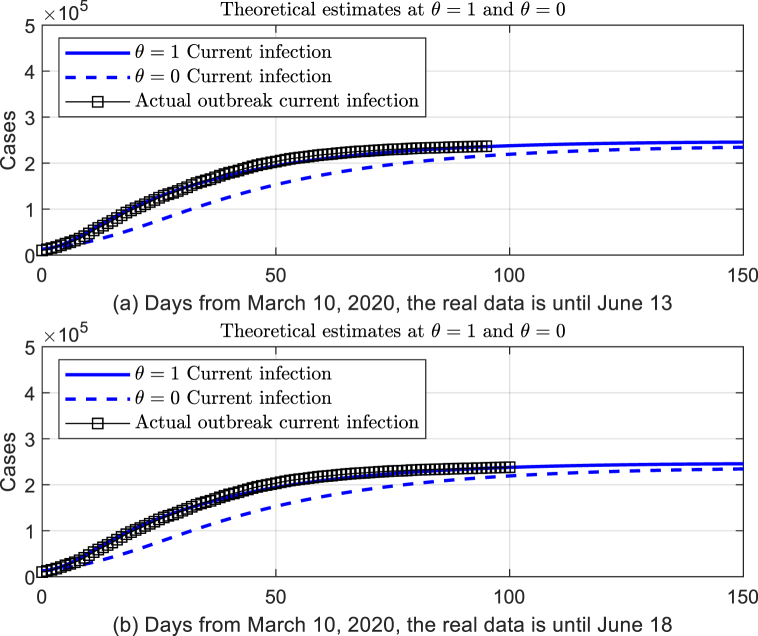
Suppose the infectivity of patients in incubation period is set by the parameter θ, and the real data fitting is coincident with the theoretical model as $\theta =1$ , which had shown 0.0297 of Mean Absolute Percentage Error. It is well concluded that the theoretical estimation of the epidemic situation by the modified SEIR model is consistent with the actual situation in Italy (see Fig. 3(a) for details).

Fig. 3.

Theoretical estimation of the modified SEIR dynamics model with and without the infection of incubation period.

It should be pointed out that the model and parameters were set according to the data before June 13. We chosen the verified data set of confirmed cases from June 14 to June 18, which shown that the fitted data from our model is consistent with the real data as the mean absolute percentage error is lower than 0.0266 (see Fig. 3(b) for details). s.

3.3. Influence estimation to containment and isolation of close contacts on the outbreak

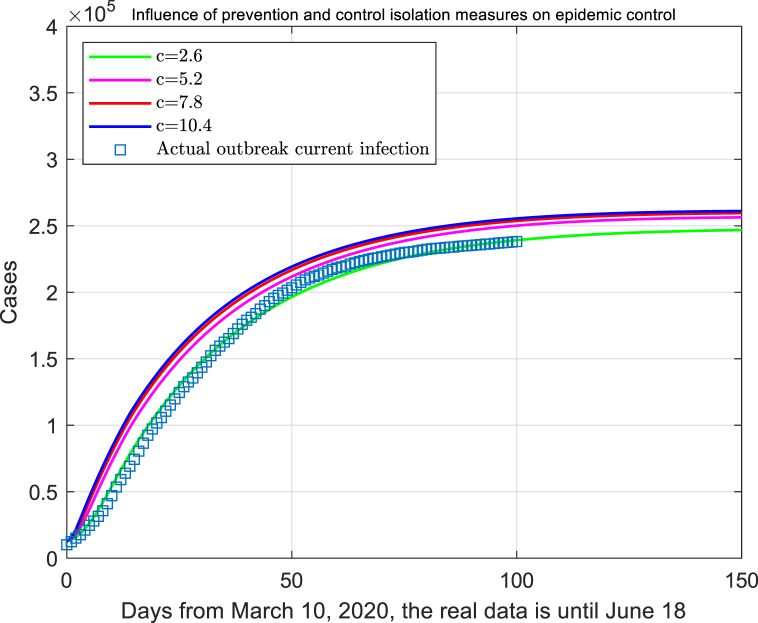
In the theoretical analysis, it is assumed that the close contacts under the current prevention and control isolation condition is 2.6. Here we simulated the infectious trend under inadequate prevention strategy through increasing the exposure rate, which is an effective measurement to access the lockdown effect. When the probability of exposure to susceptible cases is changed, the level of epidemic prevention and control has changed accordingly (assuming no change in diagnostic criteria). It concluded that the current strict control and prevention and quarantine measures have produced a good inhibitory effect to prevent the epidemic expand rapidly (Fig. 4).

Fig. 4.

Influence of infectivity during latent period on theoretical estimation of modified SEIR kinetic model.

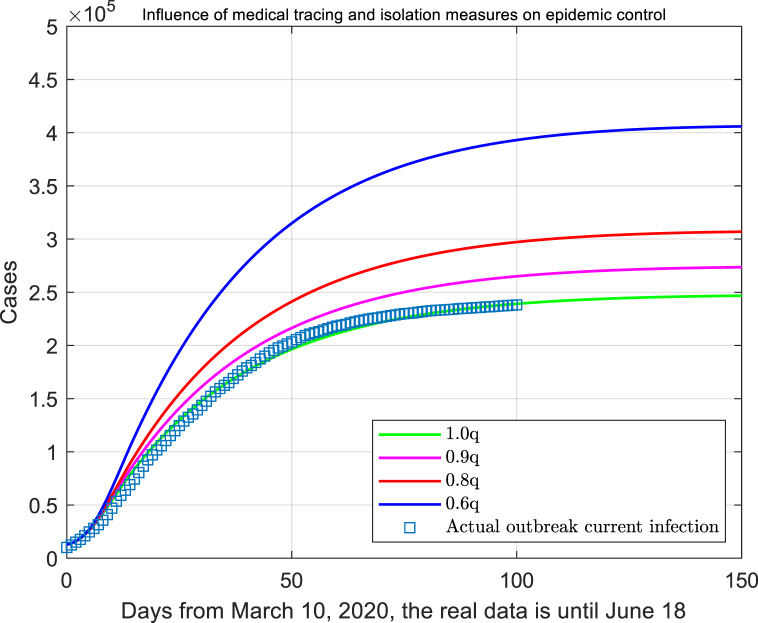
We suppose that the rigorous medical tracking isolation is carried out in Italy, which means the isolation should be taken for 14 days to those people who are in contact with the infected cases. In order to measure the influence of this circumstance, here the infectious rate varies as 0.9q, 0.8q and 0.6q. Obviously, as the isolation ratio decreases, the peak of confirmed cases will increase accordingly (assuming that the diagnostic criteria have not changed), especially to the point of 0.6, the peak number of confirmed cases have increased over 1.6 times more than the original number (Fig. 5).

Fig. 5.

The impact of medical tracking measures on isolation and control.

3.4. Assessment of the impact of centralized isolation and personal quarantine

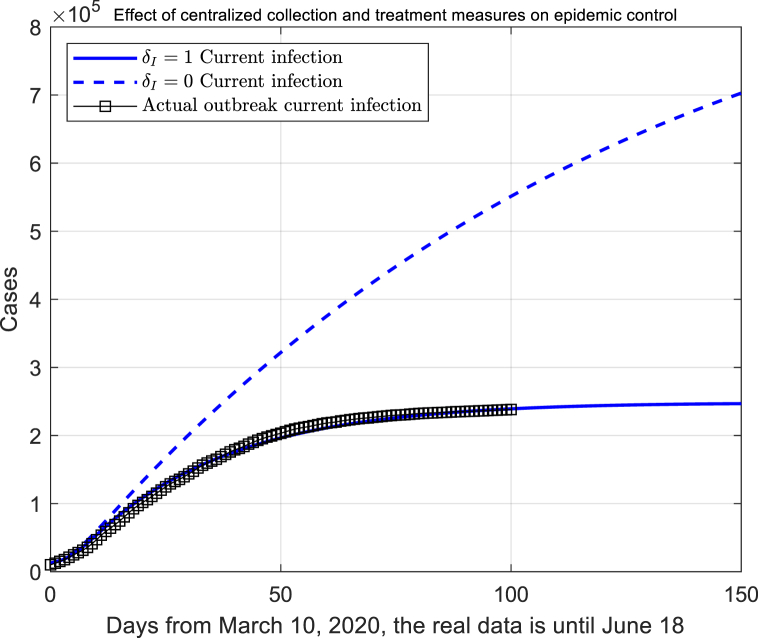
The first temporary shelter hospital was operated in the city of Cremona on March 20; an exhibition centre was transformed into Huoshenshan Hospital in ten days for supporting the creaking health system of serious infected Milan on March 30. Intensive treatment of infected patients has been launched in Italy.

The pseudo trend of infected number was simulated under no concentrated treatment (Fig. 6). The conversion rate from infected to inpatient corresponds to the parameter ${\delta }_I$ in the model (2). The capacity of centralized treatment is proportional to ${\delta }_I$ . The rate of increase in the number of infected cases has declined after 50 days, which shown that the strategy of concentrated treatment is critical to slowing the rate of new cases in Italy.

Fig. 6.

The impact of centralized isolation and personal quarantine.

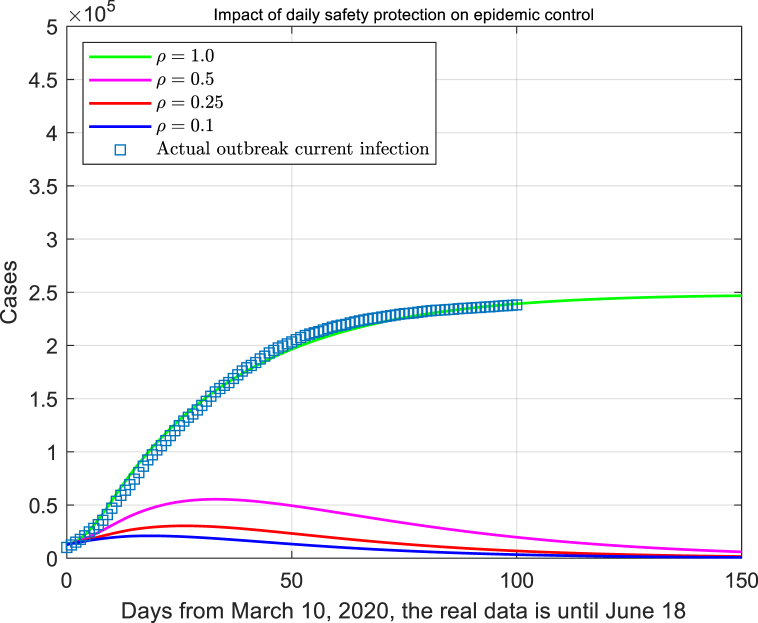
Besides, the proportion of people in contact with infected cased should also be measured. Suppose the effective contact rate is $c’=\rho c$ , where c is the daily contact rate, and ρ is the effective contact coefficient. The real data suggested the value of ρ is 1. Here we set the parameter ρ as 0.5, 0.25 and 0.1 respectively, which concluded that the smaller the contact coefficient, the less contact people with each other, then the smaller cases from the infection (Fig. 7).

Fig. 7.

The impact of daily safety precautions on outbreak control.

Updated findings suggest that the best measure is persistent and strict self-isolation. The epidemics will continue to grow, and can peak soon with the peak time depending highly on the public health interventions practically implemented (Tang et al., 2020). Steffen E. Eikenberry found that masks are useful for preventing illness in healthy people and preventing asymptomatic transmission (Eikenberry et al., 2020). Therefore, personal protection from the risk of infection is very important in curbing the epidemic extension. Strict daily precautions can make the peak time earlier and reduce the infectious number.

4. Conclusion and discussion

Effective Models have contributed vital insights into the COVID-19 pandemic, which can help evaluate and predict the effect of the implementation of different guidelines and protocols through changing parameters. We have measured the transmission capacity of potential cases and intervention of follow-up isolation, which shown the lockdown strategy effective.

The theoretical analysis of the model shows that public awareness of prevention and control, medical follow-up isolation and adequate medicine care are critical to the spread of the epidemic. Centralized treatment played a key role in the rapid decline of the peak number of infected people. The prevention and control measures of COVID-19 in Italy have been considerable for both symptomatic and asymptomatic people were screened.

We have opened a window to evaluate the effect of public health intervention and expect to search the faster way to prevent the virus. Italy is a good mode in this process. But there needs some future avenue of the work since covert transmission may be the main mode of spread, and its role is severely underestimated, which may be still on the risk of a second epidemic peak in global.

Funding

None.

Author contributions

Y.D. and L.G. wrote the first draft of the manuscript and worked on subsequent versions of the manuscript. All authors contributed to writing and interpretation of results. All authors read and approved the final manuscript.

Declaration of competing interest

The authors declare that they have no known competing or conflicting financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling editor: Jianhong Wu