Figure 5. Isolation of slow-growing species from human stool microbiota.
(a) The rank-abundance curves show that sorting based on colony density changes the overall community composition. A zoomed in portion of the rank-abundance curve is shown in the inset. (b) Phylogenetic tree of ASVs which were <1% abundant in raw stool but were increased to >1% in at least one sorting experiment. The ratio of amplification for strains amplified above the 1% limit is depicted in the heat map. N.A. (shown in gray) indicates ASVs which were not amplified from <1% to>1%. The legend for the family color labels is depicted in Figure 2a.
Figure 5—figure supplement 1. Comparison between droplets and plates for the isolation and cultivation of the 6 Alistipes populations enhanced by droplet sorting shown in Figure 5b.
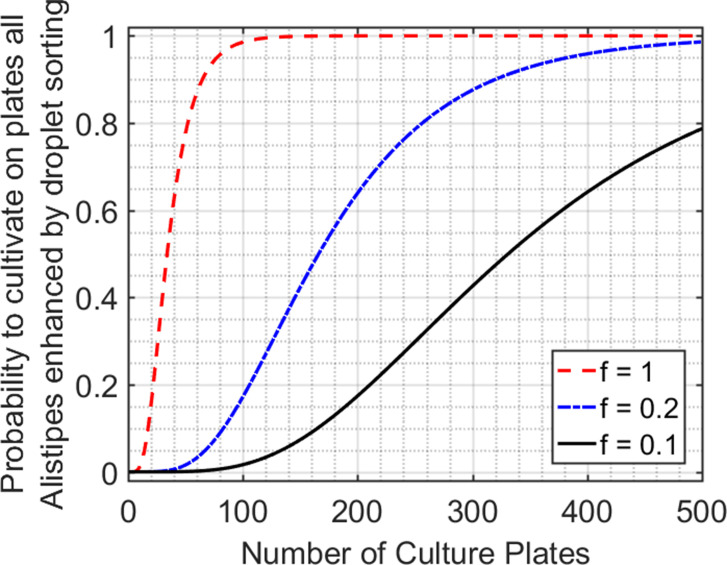
The droplet technology enables high-throughput isolation and cultivation of organisms in discrete picoliter volumes with millions of individual drops per mL of droplet emulsion. In contrast, the conventional method of low-dilution plating achieves pure strain isolation by spreading the inoculum at low enough density on agar plates so that growing colonies do not overlap. In this Supplementary Figure, we calculate the equivalent number of culture plates needed to isolate and cultivate the 6 Alistipes populations enhanced by droplet sorting. For low-dilution plating aimed at isolating slow-growing organisms, we assume a plating density of 1 cell/cm2 on a standard 100 mm circular culture plate = 78 cells/plate. The probability for a given population, X1, to be present and grow follows from binomial random sampling and is P(X1 > 0) = 1 – P(X1 = 0) = 1 – (1 – f*p1)n, where n is the number of colonies, p1 is the abundance of X1 in the initial inoculum, and f is a constant which describes the fraction of X1 which will grow in the environmental conditions. If the number of colonies is much greater than the number of populations we are aiming to grow, then P(Isolate and cultivate all populations of interest) = P(X1 > 0) * P(X2 > 0) *. . .* P(Xm > 0), where m is the number of unique populations. The figure above plots P(Isolate and cultivate the 6 droplet sorting enhanced Alistipes populations) for varying f. Even in the most optimistic scenario, where every Alistipes cell is guaranteed to grow on the low-dilution culture plate, it would still require 65 culture plates to have a 90% chance at isolating and growing all 6 populations.
Figure 5—figure supplement 2. Bacteria can be cultured on traditional plates following cultivation in droplets.
(Left) The family level relative abundance of the pooled droplets from experiment BHIS_DROPL_1D1_SORTED. (Right) The family level taxonomic assignment of 24 randomly picked colonies on a BHIS plate streaked from the same sample shown on the left. For each family detected on plate, only one genera was observed within that family. In particular, we detected Hafnia (12/24), Enterococcus (8/24), and Bacteroides (4/24).