Mutational signature learning with supervised negative binomial non-negative matrix factorization

Abstract

Motivation

Understanding the underlying mutational processes of cancer patients has been a long-standing goal in the community and promises to provide new insights that could improve cancer diagnoses and treatments. Mutational signatures are summaries of the mutational processes, and improving the derivation of mutational signatures can yield new discoveries previously obscured by technical and biological confounders. Results from existing mutational signature extraction methods depend on the size of available patient cohort and solely focus on the analysis of mutation count data without considering the exploitation of metadata.

Results

Here we present a supervised method that utilizes cancer type as metadata to extract more distinctive signatures. More specifically, we use a negative binomial non-negative matrix factorization and add a support vector machine loss. We show that mutational signatures extracted by our proposed method have a lower reconstruction error and are designed to be more predictive of cancer type than those generated by unsupervised methods. This design reduces the need for elaborate post-processing strategies in order to recover most of the known signatures unlike the existing unsupervised signature extraction methods. Signatures extracted by a supervised model used in conjunction with cancer-type labels are also more robust, especially when using small and potentially cancer-type limited patient cohorts. Finally, we adapted our model such that molecular features can be utilized to derive an according mutational signature. We used APOBEC expression and MUTYH mutation status to demonstrate the possibilities that arise from this ability. We conclude that our method, which exploits available metadata, improves the quality of mutational signatures as well as helps derive more interpretable representations.

Availability and implementation

https://github.com/ratschlab/SNBNMF-mutsig-public.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

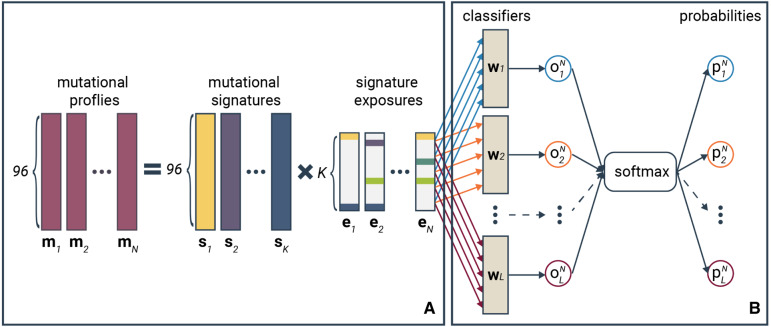
Mutational signatures are recurring patterns of sequence-context-dependent single-nucleotide variants (mutation types) observed in patients with similar etiologies. For example, lung cancer patients with an extensive smoking history share similar patterns of mutation types caused by the mutagenic effects of smoking. Recent work suggests that mutational signatures could serve as a useful biomarker that can be indicative of the underlying etiology and thus potentially contribute toward treatment decisions (Ma et al., 2018; Wang et al., 2018). A robust reference catalog set is crucial to further investigate the clinical significance of mutational signatures. To the best of our knowledge, most of the published mutational signature extraction approaches rely on non-negative matrix factorization (NMF) solutions (Alexandrov et al., 2013a, 2020; Helleday et al., 2014). NMF decomposes a mutational profile matrix, where each column is the mutational profile of a patient, into a signature matrix and an exposure matrix; the columns of the signature matrix represent the mutational signatures while each column of the exposure matrix consists of weights quantifying the presence of the mutational signatures in each patient (see Fig. 1a). SigProfiler (Alexandrov et al., 2020), one of the most commonly used approaches, assumes that the count of the trinucleotide mutational contexts are sampled from a Poisson distribution, hence used the Poisson-NMF method by Lee and Seung (2001). However, the variance in the mutation count data grows much stronger with the mean, hence violating the Poisson assumption that the mean and variance are the same. In this case, negative binomial distribution is typically a better fit in modeling count data. NMF based on negative binomial distribution has already been applied in recommendation systems (Gouvert et al., 2018) and cell-type detection in single-cell RNAseq data (Sun et al., 2019), but not yet to mutation count data for mutational signature extraction.

Fig. 1.

Schema of the SNBNMF model. (a) Mutational profile decomposition process and (b) the classification process in the SNBNMF model. In the decomposition step, the trinucleotide mutational profile of each sample is decomposed into the weighted sum of the mutational signatures, where the weights are referred as signature exposures. Each mutational profile results in a signature exposure vector given the mutational signature set. In the classification step, exposure vectors of all samples are used to classify the L-class labels of the sample (types of labels can be cancer types, histology types and etc.). ${\mathbf{w}}_l$ is the weight vector of linear classifier for class l ($l=1,\dots ,L$). The probability of sample N in class l is computed by applying the softmax function to the output of sample N from classifiers $o_l^N, \hspace{0.17em}\hspace{0.17em}l=1,\dots ,L$

Another reason to rethink the current approaches is that they are all unsupervised. This means that the best decomposition of the mutational counts into a mutational signature and exposure matrix depends solely on the mutational counts and the pre-defined number of mutational signatures provided as input. Therefore, the range of variation in the input cohort can affect the general representativeness of the mutational signatures derived from an unsupervised method. Essentially mutational signatures extracted from small patient and cancer-type limited cohorts are less robust than those from more comprehensive cancer patient cohorts when using the unsupervised approaches. Current available methods also often require complex post-processing and a potentially laborious, iterative strategy to prune out the least significant signatures so that only explanatory ones remain in the resulting signature set (Alexandrov et al., 2020).

In most cancer genomics datasets, there is usually abundant cancer metadata accompanying the mutation count data of the samples, and this metadata is not utilized by the unsupervised signature extraction method so far. Here, we extend the currently unsupervised negative binomial NMF (dubbed as NBNMF) model to supervised model for mutational signature extraction by incorporating some cancer metadata information, such as cancer type, into the framework. The integration of cancer type (metadata) is carried out in the form of adding a metadata classification loss to the objective function of the optimization problem of NBNMF. This loss acts on the exposure coefficients of the patients. Our proposed model, dubbed supervised NBNMF (SNBNMF), can exploit the available metadata of the cancer patient cohort to a greater extent compared to the unsupervised models. One benefit of supplying the signature extraction model with more information is that the derived signatures can be directed to be more representative of the mutational processes. Associating the provided information with corresponding exposures allows for direct interpretation of individual signatures. The additional information supplied, enables mutational signature extraction from smaller cohorts. The need for post-processing reduces since the according task is directly encoded in the matrix factorization loss. Finally, we also adapt SNBNMF to utilize molecular information to specifically create signatures that are predictive of the aforementioned molecular status. In other words, we can create a signature that follows a known given underlying etiology. We demonstrate this function on two examples, APOBEC activity and defective MUTYH activity highlighting this ability.

2 Materials and methods

2.1 Data

The mutational count data used in this work is based on the somatic variant calls from 2521 samples from the Pan-Cancer Analysis of Whole Genomes International Cancer Genome Consortium (PCAWG-ICGC) (The et al., 2020). The ICGC mutational signatures and exposures (Alexandrov et al., 2020) have been used to provide a comparison between mutational signatures generated by the SNBNMF and NBNMF approach and the PCAWG-ICGC effort. Here we only consider extracting signatures for single-base-substitution (SBS) mutations. The mutation type we use is a trinucleotide sequence consisting of the mutated base and its immediate 3′ and 5′ sequence context, and the total number of mutation types is 96. Metadata information available in the PCAWG-ICGC includes project code, histology type, APOBEC expression and OxoG score among others. For this paper, we incorporate the project code information into the signature extraction process using our SNBNMF model because the project code labels encode both the cancer type and the country information of the patients. Examples of the project code label in the ICGC consortium data are BRCA-EU, BRCA-CN and PACA-AU. Supplementary Figure S1 provides an example of the mutational profile and also shows the distribution of the multi-class label we used.

2.2 Negative binomial NMF

We denote the mutational profile of the nth cancer patient as ${\mathbf{m}}_n={(m_{1n},m_{2n},\dots ,m_{Jn})}^T\in {\mathbb{Z}}_{+}^J$, where m_jn is the non-negative integer count of mutation type j and J is the total number of mutation types. NMF decomposes the mutational profile matrix $\mathbf{M}\in {\mathbb{Z}}_{+}^{J\times N}$, formed by all N patients in the cohort, into a signature matrix $\mathbf{S}\in {ℝ}_{+}^{J\times K}$ and an exposure matrix $\mathbf{E}\in {ℝ}_{+}^{K\times N}$:

$$\left[\begin{array}{ccc}{\mathbf{m}}_1& \cdots & {\mathbf{m}}_N\end{array}\right]=\mathbf{M}\approx \mathbf{S}\mathbf{E}=\left[\begin{array}{ccc}{\mathbf{s}}_1& \cdots & {\mathbf{s}}_K\end{array}\right]\left[\begin{array}{ccc}{\mathbf{e}}_1& \cdots & {\mathbf{e}}_N\end{array}\right].$$ (1)

${\mathbf{s}}_k$ in Equation (1) is the kth signature derived by NMF, and K is total number of signatures that we want NMF to extract from the mutational profile matrix. The kth element of ${\mathbf{e}}_n=(e_{1n},e_{2n},\dots ,e_{Kn})$, the nth column of the exposure matrix, encodes the exposure of patient n to signature k. The higher the exposure value is, the more influence from the mutational process associated with the corresponding signature have in the patient.

The negative binomial distribution allows to account for over-dispersion (Love et al., 2014) that we observe in mutational count data Supplementary Figure S2. The over-dispersion in the NB distribution is modeled by the parameter α:

$$\text{Var}\left(m_{jn}\right)=\mathbf{E}\left[m_{jn}\right]\left(1+\frac{\mathbf{E}\left[m_{jn}\right]}{\alpha }\right)>\mathbf{E}\left[m_{jn}\right].$$

The maximum likelihood estimator of S and E is equivalent to minimizing the negative log-likelihood function:

$$\begin{array}{l}-\text{log}\hspace{0.17em}P(\mathbf{S},\mathbf{E})=-\sum _{j=1}^J\sum _{n=1}^N\hspace{0.17em}\text{log}\hspace{0.17em}\left(\frac{\Gamma (m_{jn}+\alpha )}{m_{jn}!\Gamma (\alpha )}\frac{{(\alpha /{\overline{m}}_{jn})}^{\alpha }}{{(1+\alpha /{\overline{m}}_{jn})}^{m_{jn}+\alpha }}\right)\\ =\sum _{j=1}^J\sum _{n=1}^N((m_{jn}+\alpha )\hspace{0.17em}\text{log}\hspace{0.17em}({\overline{m}}_{jn}+\alpha )-m_{jn}\hspace{0.17em}\text{log}\hspace{0.17em}{\overline{m}}_{jn})\\ +C_0,\end{array}$$

where ${\overline{m}}_{jn}={\left[\mathbf{S}\mathbf{E}\right]}_{jn}$ is the constructed mutation count of mutational context j in sample n. C₀ is an invariant with respect to S and E since

$$C_0=-JN\alpha \hspace{0.17em}\text{log}\hspace{0.17em}\alpha -\sum _{j=1}^J\sum _{n=1}^N\hspace{0.17em}\text{log}\hspace{0.17em}\frac{\Gamma (m_{jn}+\alpha )}{m_{jn}!\Gamma (\alpha )}.$$

Therefore, minimizing $-\text{log}\hspace{0.17em}P(\mathbf{S},\mathbf{E})$ is equivalent to minimizing

$${\mathcal{L}}_r=\sum _{j=1}^J\sum _{n=1}^N((m_{jn}+\alpha )\hspace{0.17em}\text{log}\hspace{0.17em}({\overline{m}}_{jn}+\alpha )-m_{jn}\hspace{0.17em}\text{log}\hspace{0.17em}{\overline{m}}_{jn})$$ (2)

We use the majorization-minimization (MM) algorithm (Févotte and Idier, 2011), an iterative algorithm, to solve the optimization problem in Equation (2). The MM algorithm constructs an auxiliary function $G(x,\tilde{x})$ to the objective function F(x), where the auxiliary function must satisfy $G(x,\tilde{x})\ge F\left(x\right)$ and $G(x,x)=F\left(x\right)$. Minimizing the auxiliary function $G(x,\tilde{x})$ guarantees that F(x) is non-increasing with the update $x^{t+1}=\text{arg}{\min }_{x}G(x,x^t)$ (Févotte and Idier, 2011; Lee and Seung, 2001). Therefore, we first construct

$$G(E;\tilde{E})={\displaystyle \sum _{j=1}^J{\displaystyle \sum _{n=1}^N(}}-m_{jn}{\displaystyle \sum _{k=1}^K\frac{s_{jk}{\tilde{e}}_{kn}}{{[S\tilde{E}]}_{jn}}}\log \left(\frac{{[S\tilde{E}]}_{jn}}{{\tilde{e}}_{kn}}{e}_{kn}\right)+\frac{m_{jn}+\text{α}}{{[S\tilde{E}]}_{jn}+\text{α}}{\displaystyle \sum _{k=1}^K{s}_{jk}}(e_{kn}-{\tilde{e}}_{kn})+(m_{jn}+\text{α})\log ({[S\tilde{E}]}_{jn}+\text{α}) )$$

and

$$G(S;\tilde{S})={\displaystyle \sum _{j=1}^J{\displaystyle \sum _{n=1}^N(}}-m_{jn}{\displaystyle \sum _{k=1}^K\frac{s_{jk}{\tilde{e}}_{kn}}{{[\tilde{S}E]}_{jn}}}\log \left(\frac{{[\tilde{S}E]}_{jn}}{{\tilde{s}}_{jk}}{s}_{jk}\right)+\frac{m_{jn}+\text{α}}{{[\tilde{S}E]}_{jn}+\text{α}}{\displaystyle \sum _{k=1}^K(s_{jk}-{\tilde{s}}_{jk})}{e}_{kn}+(m_{jn}+\text{α})\log ({[\tilde{S}E]}_{jn}+\text{α}) ),$$

where $G(\mathbf{E};\tilde{\mathbf{E}})$ is the auxiliary function to ${\mathcal{L}}_r$ in Equation (2) for E and $G(\mathbf{S};\tilde{\mathbf{S}})$ is the auxiliary function for S. By setting the partial derivative of $G(\mathbf{E};\tilde{\mathbf{E}})$ and $G(\mathbf{S};\tilde{\mathbf{S}})$ to zero, we derived the multiplicative updates for E and S, the details of which is shown in Equations (3) and (4) respectively.

$$e_{kn}\leftarrow e_{kn}\frac{{\sum }_{j=1}^J\frac{m_{jn}}{{\overline{m}}_{jn}}{s}_{jk}}{{\sum }_{j=1}^J\frac{m_{jn}+\alpha }{{\overline{m}}_{jn}+\alpha }{s}_{jk}},$$ (3)

$$s_{jk}\leftarrow s_{jk}\frac{{\sum }_{n=1}^N\frac{m_{jn}}{{\overline{m}}_{jn}}{e}_{kn}}{{\sum }_{n=1}^N\frac{m_{jn}+\alpha }{{\overline{m}}_{jn}+\alpha }{e}_{kn}}.$$ (4)

Normalization on ${\mathbf{s}}_k$ is performed after the objective function in Equation (2) has converged so that each entry of the signature represents the frequency of the corresponding mutational context, and the exposures are multiplied by the corresponding normalization factors such that the multiplication of S and E remains unchanged. The normalization steps are shown as the following

$$e_{kn}\leftarrow e_{kn}·\left(\sum _{j=1}^J{s}_{jk}\right),$$ (5)

$$s_{jk}\leftarrow \frac{s_{jk}}{{\sum }_{j=1}^J{s}_{jk}}.$$ (6)

2.3 Signature extraction with supervised NBNMF

Formally, we use the exposures ${\mathbf{e}}_n$a posteriori in support vector machines (SVMs) to classify the labels. The output of the SVM for class l where the input is the exposure vector of sample n is denoted as

$$z_{ln}={\mathbf{w}}_l^{\mathrm{\top }}{\mathbf{e}}_n+b_l.$$

The optimal SVM classifiers are learned by minimizing the classification loss

$${\mathcal{L}}_c=\sum _{l=1}^L\sum _{n=1}^N{\beta }_{ln}\max \{0,1-y_{ln}{z}_{ln}\}+\frac{{\lambda }_w}{2}\left|\right|\mathbf{W}|{|}_F^2,$$ (7)

where L is the number of label classes, ${\mathbf{w}}_l$ and b_l are the weight vector of the SVM classifier for the lth class, β_ln is the loss weight of sample n for the lth class and λ_w is the hyperparameter that controls for overfitting. Our model has two modes: one takes into account the imbalance in class distribution,

$${\beta }_{ln}=\frac{{\sum }_{n\in \{m:y_{lm}<0\}}\left|y_{ln}\right|}{{\sum }_{n\in \{m:y_{lm}>0\}}\left|y_{ln}\right|},$$

when y_ln = 1, otherwise ${\beta }_{ln}=1$; the other mode ignores the class imbalance, where β_ln is always set to 1.

Figure 1 shows a diagram of the supervised NBNMF model. Here we choose to use SVMs as the classifiers because the hinge loss function of SVMs is locally linear with respect to the exposures, making the optimization problem easier by using the MM method. The objective of the supervised dictionary learning model is the weighted sum of Equations (2) and (7):

$$\underset{\mathbf{S},\mathbf{E},\mathbf{W},\mathbf{b}}{\min }{\mathcal{L}}_r+{\lambda }_c{\mathcal{L}}_c,$$ (8)

where λ_c is the hyperparameters which controls the trade-off between the reconstruction loss and the classification performance. To minimize Equation (8), we update its auxiliary loss function for E and compute a new auxiliary loss function for W

$$G\prime (\mathbf{E},\tilde{\mathbf{E}})={\lambda }_c\sum _l\sum _n\sum _k{\beta }_{ln}\frac{w_{kl}{\tilde{e}}_{kn}}{{\mathbf{w}}_l^{\mathrm{\top }}{\tilde{\mathbf{e}}}_n}·H_{ln}\left(b_l+\frac{{\mathbf{w}}_l^{\mathrm{\top }}{\tilde{\mathbf{e}}}_n}{{\tilde{e}}_{kn}\left|\right|{\mathbf{m}}_n|{|}_1}{e}_{kn}\right)+\frac{{\lambda }_c{\lambda }_w}{2}\sum _l\left|\right|\mathbf{w}|{|}_l^2+G(\mathbf{E};\tilde{\mathbf{E}}),$$

$$\begin{array}{l}G(\mathbf{W},\tilde{\mathbf{W}})={\lambda }_c\sum _l\sum _k\sum _n{\beta }_{ln}\frac{{\tilde{w}}_{kl}{e}_{kn}}{{\tilde{\mathbf{w}}}_l^{\mathrm{\top }}{\mathbf{e}}_n}·H_{ln}\left(b_l+\frac{{\tilde{\mathbf{w}}}_l^{\mathrm{\top }}{\mathbf{e}}_n}{{\tilde{w}}_{kl}\left|\right|{\mathbf{m}}_n|{|}_1}{w}_{kl}\right)\\ +\frac{{\lambda }_c{\lambda }_w}{2}\sum _l\sum _k{w}_{kl}^2+C,\end{array}$$

where $H_{ln}\left(z\right)=\max \{0,1-y_{ln}z\}$ is the hinge loss function. Subsequently, the update steps for solving Equation (8) are

$$e_{kn}\leftarrow e_{kn}\frac{{\sum }_{j=1}^J\frac{m_{jn}}{{\overline{m}}_{jn}}{s}_{jk}}{{\sum }_{j=1}^J\frac{m_{jn}+\alpha }{{\overline{m}}_{jn}+\alpha }{s}_{jk}-{\lambda }_c{\sum }_{l\in {\ell }_n}^{}{\beta }_{ln}\frac{w_{kl}{y}_{ln}}{\left|\right|{\mathbf{m}}_n|{|}_1}},$$

where ${\mathcal{L}}_n=\{l:y_{ln}({\mathbf{w}}_l^{\mathrm{\top }}{\mathbf{e}}_n+b_l)<1\};$

$$\begin{array}{l}{\mathbf{w}}_l\leftarrow {\mathbf{w}}_l-{\eta }_t\left({\lambda }_w{\mathbf{w}}_l-\sum _{n\in {\mathcal{N}}_l}{\beta }_{ln}\frac{y_{ln}{\mathbf{e}}_n}{\left|\right|{\mathbf{m}}_n|{|}_1}\right), \\ b_l\leftarrow b_l+{\eta }_t\sum _{n\in {\mathcal{N}}_l}{\beta }_{ln}{y}_{ln}, \end{array}$$

where

$${\mathcal{N}}_l=\{n:y_{ln}({\mathbf{w}}_l^{\mathrm{\top }}{\mathbf{e}}_n+b_l)<1\}.$$

η_t is the learning rate for updating the classification parameters ${\mathbf{w}}_l$ and b_l.

2.4 Signature attribution

Like any supervised approach, SNBNMF requires a training step. The result of the decomposition described above [Equation (8)] results in an exposure matrix for the training samples and a set of mutational signatures. To reduce the variance and increase robustness, we used the cluster centers of the clustering results on all the signatures learned from 10 runs as the final set of signatures, but the final set of exposures cannot be simply by taking the average of the exposures because

$$\frac{1}{10}\sum _{p=1}^{10}{\mathbf{S}}^{\left(p\right)}{\mathbf{E}}^{\left(p\right)}\ne \left(\frac{1}{10}\sum _{p=1}^{10}{\mathbf{S}}^{\left(p\right)}\right)\left(\frac{1}{10}\sum _{p=1}^{10}{\mathbf{E}}^{\left(p\right)}\right),$$

where ${\mathbf{S}}^{\left(p\right)}$ and ${\mathbf{E}}^{\left(p\right)}$ are the signature matrix and exposure matrix learned at the pth run. Therefore, we re-attribute exposures to the entire dataset by fixing the S to the final set of signatures and only update E in the model shown in Equation (1). The attributed signatures have non-zero exposure values, and the exposure values correlate with the importance of the signatures in the samples.

The major difference between signature attribution and signature extraction is that during the signature attribution step the count matrix used includes the counts of the full patient cohort. Also, the mutational signature matrix S is fixed in the signature attribution process whereas the signature extraction process is used to learn the parameter S. The exposure matrix E is updated according to (3). In addition, no metadata information is required by the signature attribution process, so it can be applied to any newly collected mutational profile even without any additional metadata information.

We add a common post-processing step also used by other tools (Alexandrov et al., 2020). After the signature attribution process converges, we trim the computed exposures. It is a fine-tuning procedure to increase the overall sparsity of the exposure matrix by removing exposures that do not increase the cosine similarity between the original mutational profile and the reconstructed mutational profile by more than 0.01. In those cases, the exposure weight is simply set to 0. The trimming step results in a smaller but more relevant attributed signature set by removing the likely irrelevant signatures from it.

2.5 Signature matching

To analyze the quality of the signature sets extracted by our proposed method, we need to match signatures in the learned signature set (NBNMF or SNBNMF) with the ICGC reference set (Alexandrov et al., 2020). The distance between two signatures is quantified using a cosine correlation similarity, which ranges between 0 and 1. The cosine similarity between signature s and $\mathbf{s}\prime$ is computed using the following equation

$$\text{sim}(\mathbf{s},\mathbf{s}\prime )=\frac{\langle \mathbf{s},\mathbf{s}\prime \rangle }{\left|\right|\mathbf{s}\left|\right|\left|\right|\mathbf{s}\prime \left|\right|}.$$

When the cosine similarity between two signatures equals to 1, the pair of signatures are exactly the same; and when the cosine similarity equals to 0, these signatures share no similarity. When matching two signature sets $\mathcal{A}$ and $\mathcal{B}$, for every signature in $\mathcal{A}$, its cosine similarity with every signature in $\mathcal{B}$ is computed, we consider the pair with the highest cosine similarity a match.

2.6 Evaluation

The quality of the mutational signature set is evaluated using two criteria: (i) the reconstruction error using the signatures and exposures and (ii) the classification accuracy on the sample exposures to the dictionary.

Reconstruction error: The reconstruction error evaluates how well the mutational profiles can be reconstructed with the mutational signatures that we learned. A good set of mutational signatures should be able to reconstruct the mutational profiles, otherwise the mutational signatures are not representative of the mutational process at all. Here, we use the Frobenius reconstruction error $\left|\right|\mathbf{M}-\mathbf{S}\mathbf{E}|{|}_F^2/N$ to measure the error between the original and reconstructed mutational profiles (Alexandrov et al., 2013a).

Classification accuracy: We also required mutational signatures to not only be reconstructive but also discriminative. This means that the exposure values learned should be informative to classify the cancer type (metadata) of the samples. To evaluate the discriminative power of the mutational signature set, we applied SVMs to the exposures computed from the signature attribution process and report the classification accuracy.

2.7 Experimental setup

We learn the dictionary by training the model on the entire dataset, and use random search for hyperparameter optimization. The hyperparameters of the models are the regularization parameters and the number of signatures. The hyperparameters of the training processes include learning rates, decaying rate and decaying step of the learning rate for different variables. For a given number of signatures K, we repeat the training process 10 times with different initialization values for S and E, and then use agglomerative hierarchical clustering to group the signatures from these 10 runs into K clusters. The hierarchical clustering technique we use is complete-linkage clustering and the distance metric used in clustering is cosine similarity. The final set of signatures corresponding to each signature size value K are the centers of the K clusters. To select the optimal signature size, we choose the signature set with high classification accuracy, as well as high average silhouette width (Rousseeuw, 1987) which measures the reproducibility of the signatures. Given a data point i, denoting the mean distance from data point n to all other data points in the same cluster as n as a(n), and the minimal average distance from data point n to all points in any other cluster as b(n), the silhouette of data point i is defined as $\left(b\right(n)-a(n\left)\right)/\max \left\{a\right(n),b(n\left)\right\}$ if the cluster that data point n consists of more than one data point. During evaluation on the classification performance, we partition the data into training and test sets with ratio 5:1, and the training set is further partitioned into five folds for cross-validation on the classification model hyperparameter selection (shown in Fig. 2). The frequency distribution of the labels is preserved during partitioning.

Fig. 2.

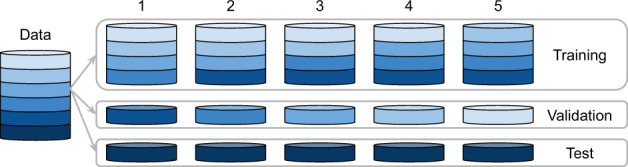
Data-splitting schema

2.8 Robustness testing

To test the effect of the supervised regularization term in SNBNMF against NBNMF, we took six cancer types with the highest number of patients in the PCAWG-ICGC cohort (Project Code: LIRI, PACA, BRCA, PRAD, PBCA and OV) resulting in a total of 1059 patients. The patients were binned into six equal-sized bins and we used the experimental set-up described above repeatedly using random bins to derive mutational signatures with SNBNMF. Cosine distances were used to evaluate the variation across deriving mutational signatures with different subsets as well as the distance to the current reference signature.

2.9 SNBNMF with molecular labels

The supervision loss can be used for more than just generating robust mutational signatures. Adding a second supervision loss with a molecular label allows us to create specific mutational signatures that are shaped by the individual feature. In order to do this we constrained one signature (Signature 1) to follow the supervision term with molecular features. The resulting signature 1 should then be driven by the molecular feature used. We performed three experiments.

FPKM-UQ values from the PCAWG-ICGC project (Calabrese et al., 2020) have been used to assess over and under expression of APOBEC (we used the sum of APOBEC3A and APOBEC3B expression). Patients were binned into 10 bins using a uniform split between 0 and 100. For each bin, we added a classification loss.

We used clinvar (Landrum et al., 2018) to retrieve a list of variants in the MUTYH gene that are considered pathogenic and confirmed by clinical testing. In total, we found 64 patients that harbored at least one of these variants in the ICGC cohort.

We also utilized the OxoG scores from the PCAWG-ICGC project to try to recapitulate the technical artifacts observed from oxidized guanine. This experiment was done to only assess the principle capabilities of using additional factors to derive mutational signatures. For this we binarized the OxoG score into high (>80) and low.

3 Results

In order to demonstrate the performance and abilities of SNBNMF we set up experiments to test the following features:

1. SNBNMF yields signatures of which the corresponding exposures are more consistent with cancer types, shown in Table 1.

2. SNBNMF requires less post-processing and is able to recover known mutational signatures with clear etiologies. This is demonstrated by comparing SNBNMF signatures with ICGC derived signatures using SigProfiler (Alexandrov et al., 2020), shown in Fig. 4.

3. SNBNMF is able to recover mutational signatures using cohorts with smaller sample sizes, shown in Figure 5b.

4. SNBNMF is more flexible allowing arbitrary cofactors to guide the signature extraction process. Given a factor that is known to drive a mutational signature, this factor can be used to derive the according mutational signature specifically. We demonstrate this on two examples (MUTYH status and APOBEC expression).

Table 1.

Average Frobenius reconstruction error and average classification error of all samples using different approaches to derive mutational signatures

Method	Reconstruction error	Classification accuracy
ICGC (Alexandrov et al., 2020)	80, 720, 711	0.536 ±0.009
NBNMF	26, 678, 521	0.506 ±0.008
SNBNMF	15, 725, 795	0.554 ±0.019

Note: The accuracy from a random classifier is 0.037 ± 0.008.

Fig. 4.

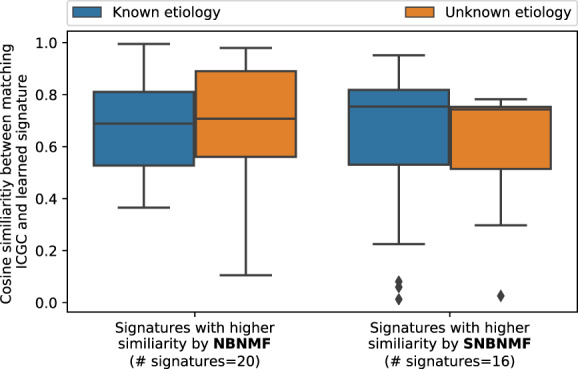
Left set of boxplots depicts the cosine similarities of those signatures where the NBNMF approach has a higher cosine similarity to the reference signature than the SNBNMF approach. Right set of boxplots shows the cosine similarities where SNBNMF has higher cosine similarities to the reference set. The number of signatures is a hyperparameter, and after hyperparameter optimization, the best number of signatures found for SNBNMF and NBNMF is 20 and 16, respectively. The plot summarizes Supplementary Figure S3A with the orange boxplots representing signatures with unknown etiology and blue boxplots representing signatures with known etiology

Fig. 5.

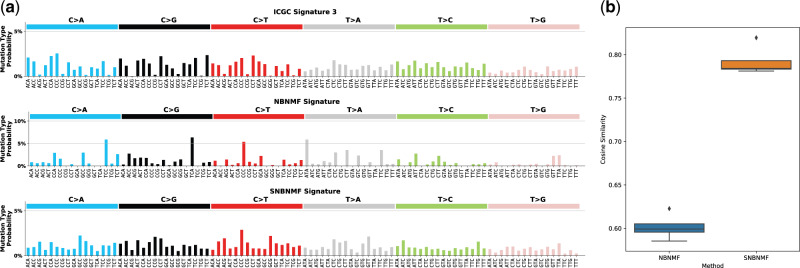
(a) Signatures best matched with ICGC signature 3 learned by NBNMF and SNBNMF methods from sub-population with only six cancer types (top: ICGC signature 3; middle: NBNMF signature matched with ICGC signature 3; bottom: SNBNMF signature matched with ICGC signature 3). (b) Boxplots of cosine similarity between ICGC signature 3 and NBNMF/SNBNMF signatures that are learned from subpopulation with only six cancer types and are matched with ICGC signature 3

3.1 SNBNMF signatures have higher overall quality

Using the mutational signature data from the ICGC cohort allows us to compare signatures generated by the current state-of-the-art approach annotated as ICGC signature set (Alexandrov et al., 2020) which is identical to COSMIC SBS signature set in version 3, the NBNMF method (Gouvert et al., 2018) (representative of a baseline NMF approach without post-processing) and the proposed SNBNMF approach. Here we compare these different mutational signature learning methods based on the evaluation criteria discussed in Section 2.6. Table 1 shows the average reconstruction error and average classification accuracy of the 45 cancer types (shown in Supplementary Fig. S1b) on different mutational signature sets; and Figure 3 shows the cosine similarity between the ICGC signature set and signature set derived by NBNMF/SNBNMF.

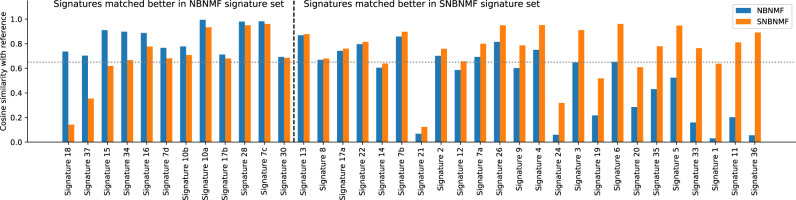
Fig. 3.

Cosine similarity between the matching pairs of ICGC signature and signature learned by NBNMF/SNBNMF. ICGC signatures that are better matched in the signature set learned by NBNMF are on the left side of the black dashed line, and signatures that are better matched in the signature set learned by SNBNMF are on the right. The signatures are sorted in the order that the difference between the cosine similarities of the ICGC-SNBNMF signature pair and the ICGC-NBNMF signature pair increases. The gray-dotted line indicates 0.65 cosine similarity, which we use as a threshold for good matching pairs. Most of the signatures that are much better matched using NBNMF, such as signature 37, 34 and 16 has no proposed etiology by COSMIC; while most of the signatures that are much better matched by SNBNMF, such as 9, 4, 3, 6, 35, 33, 11 and 36 have certain proposed etiology

SNBNMF signatures and corresponding exposures achieve a lower reconstruction error and higher classification accuracy demonstrating that the utilization of annotation information during the signature learning stage can improve the signature quality.

The average cosine similarity of matches between the reference set and the signature set learned NBNMF is 0.6184, while the average cosine similarity of matches between the reference set and the signature set learned by SNBNMF is 0.7224.

3.2 SNBNMF requires less post-processing

Here we compare signature 4 known to be associated with smoking (Alexandrov et al., 2013b), using ICGC, NBNMF and SNBNMF signature sets (shown in Supplementary Fig. S4). This comparison qualitatively illustrates the difference between using an unsupervised versus a supervised approach. The signature generated from our proposed approach has a closer resemblance to ICGC signature 4, compared to the unsupervised approach. NBNMF signature 4 can be considered the intermediary output of the approach that leads to the generation of ICGC signature 4 without the post-processing steps mentioned previously. Our integrated solution that penalizes dispersed exposure coefficients can generate the desired mutational signature directly. Supplementary Figure S10 gives an overview of the remaining mutational signatures learned by SNBNMF.

In order to quantitatively evaluate how well the unsupervised method (i.e. NBNMF) and the proposed supervised method (i.e. SNBNMF) resemble the state-of-art ICGC signature set, we examine the cosine similarities of the generated signatures to the reference set (ICGC). We observe that the cosine similarities are shifted upwards (Supplementary Fig. S3B). An in-depth look shows that both signatures seem to perform similarly in reconstructing the ICGC reference signatures but that the SNBNMF approach seems to be more robust in cases of signatures with unknown etiology (see Fig. 4; Supplementary Fig. S3A).

3.3 SNBNMF generates more robust mutational signatures

The typical approach of a matrix factorization on the mutation count matrix of a cohort of patient samples makes the resulting signatures dependent on the overall composition of the cohort. Depending on the size of the cohort, the result can be significantly skewed. An example using a subset of 1059 patients (the training set size is 707) of the six most common cancer types (liver, pancreatic, breast, prostate, pediatric brain and ovarian cancers) in the PCAWG-ICGC cohort illustrates the problem. Figure 5a shows the signature that has the highest cosine similarity with the reference ICGC signature 3 out of all five random subsets using NBNMF and SNBNMF using project codes as label (see Supplementary Fig. S5 for all signatures that have been matched to ICGC signature 3). The SNBNMF approach yields signatures that show significantly more robustness on different subpopulations and the best matching with ICGC signature 3 also looks qualitatively and quantitatively (the cosine similarity is 0.78 as shown in Fig. 5b) more similar. In total, we observe a higher overall cosine similarity (0.52 versus 0.46) with known mutational signatures using a subset of the ICGC cohort than using the NBNMF approach. Using the individual random subsets, we observe that SNBNMF outperforms NBNMF consistently in terms of similarity to the reference dataset (see Supplementary Fig. S6). We believe that these results imply that SNBNMF addresses the influence of different subpopulations in the mutational signature generation which can be particularly useful in cases where only small patient cohorts are available.

3.4 SNBNMF can be used to generate signatures with given labels

A disadvantage of the standard matrix factorization approach is that the resulting signatures may not necessarily reflect biology. Increasing the number of signatures in the decomposition step, can lead to diluting the signal and potentially decomposing different sources of noise. The current approach is to post-match the derived mutational signatures to the known reference signatures limiting the ability to derive mutational signatures with interesting unknown etiologies. The advantage of SNBNMF is that it can be adapted to direct mutational signature generation by integrating biological signals. To demonstrate this we examined two cases more closely (APOBEC gene expression and MUTYH mutation status).

3.4.1 APOBEC gene expression

APOBEC3a and APOBEC3b genes are known to be involved in cytidine deaminase functions (Burns et al., 2013; Refsland and Harris, 2013; Roberts et al., 2013; Wang et al., 2018). Thus, up-regulation of APOBEC gene expression is typically observed in conjunction with signature 2. SNBNMF can be adapted to use the prediction of APOBEC expression (sum of APOBEC3a and APOBEC3b) in a supervised learning task. This allows us to illustrate the usage of SNBNMF to generate mutational signatures from molecular signals and therefore enable the identification of interpretable mutational signatures. We constrained the first signature to be predictive of APOBEC expression status and compare the resulting signature with the ICGC reference signature 2 and 13 (known to be related to APOBEC expression). Supplementary Figure S7 shows that we can create an APOBEC expression derived signature that resembles a combination of signature 2 and 13 with the C to T transitions having a partially different context.

3.4.2 MUTYH status

Mutations in the gene MUTYH are associated with 8-oxoguanine presence that create a distinct OxoG signature reported previously (Viel et al., 2017). Here, we utilize the MUTYH mutation status to define a patient class membership. We have again constrained the first signature to be predictive of the mutation status. SNBNMF is able to recover a signature, similar to the previously reported OxoG signature expected to be observed in patients with MUTYH status (see Supplementary Fig. S8). We do observe differences which we believe is due to the small case numbers available to us. Only 65 patients in our cohort have a MUTYH mutation that is considered functional and validated and thus the signatures generated do not resemble exactly the signature shown previously. We have also ran the same experiment using the OxoG Score from the ICGC effort. Here a similar but not identical OxoG signature is observed due to technical artifacts (Costello et al., 2013). As a proof of concept, we utilize this score to show the performance of SNBNMF trying to derive this OxoG signature (see Supplementary Fig. S9) showing some similarity but also differences between these signatures.

4 Discussion

We designed and implemented a novel supervised negative binomial matrix factorization approach. An SVM loss was used to extend the NBNMF framework to allow for integration of additional metadata. This tool was applied on the PCAWG-ICGC dataset (Alexandrov et al., 2020; The et al., 2020) allowing for an extensive comparison of signatures between different approaches.

Our results show that mutational signature generation from a supervised matrix factorization solution is preferable over an unsupervised set-up. We achieve significantly higher cancer-type prediction accuracy using the SNBNMF exposures and a smaller reconstruction error while we can still reproduce the reference mutational signatures generated previously (Alexandrov et al., 2020). SNBNMF allows us to forego most of the post-processing that is typically done on mutational signatures, making our method more approachable and easier to apply than other available options. Also, SNBNMF is particularly well suited for mutational signature generation on small cohorts since the supervised term allows for the integration of metadata that will guide the decomposition. We also showed how SNBNMF can be used to adapt the regularization term to specifically generate mutational signatures based on molecular features by using APOBEC expression or MUTYH mutation status as a label. It would even be possible to adapt the same model to account for confounding factors by using this factor as a label in the classification loss.

Penalizing non-predictive exposure coefficients enforces our notion that the mutational pattern is specific to different cancer types due to their vast differences in etiology. It is important to note that this does not penalize or prevent signatures being shared across cancer types. No post-processing or iterative refinement strategies are needed to derive mutational signatures. We only apply a trimming step on the exposure matrix also used by others.

We noticed that NBNMF and SNBNMF comparison against ICGC signatures show higher cosine similarities particularly for signatures of known etiology. There are two possible explanations for this. Either, the signatures of unknown etiology capture a lot of the overall noise that is then redistributed under a different NMF model, or these signatures are reflecting more complex patterns that are partially shared across cancer types. The exposure coefficients derived from this approach allow us to relate individual signatures to activation in specific cancer types. Similarly, other metadata information (e.g. smoking history) can be used to investigate the activation of signatures in the according categories. An open challenge is how to compare quantitatively, reliably and systematically two given mutational signatures. Given that the frequency profile is often sparse, the cosine distance is sometimes driven by the differences in the overall noise and thus preventing or creating misleading matches. A bootstrapped cosine similarity (Huang et al., 2018) could potentially address the problem and is worth considering in future work. Evaluation has been further complicated by the fact that SNBNMF is expected to generate slightly different signatures that are intended to have overall better properties. We did opt for a comparison to the ICGC signatures as a reference set with the reasoning that mutational signatures with known underlying biology should also be found using our approach.

We hope that the integration of a supervision signal based on the exposure matrix opens up a new strategy to incorporate clinical or molecular knowledge into the mutational signature direction potentially making these signatures more interpretable in the future.